Related Research Articles

The ecliptic or ecliptic plane is the orbital plane of Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic against the background of stars. The ecliptic is an important reference plane and is the basis of the ecliptic coordinate system.
A solar equinox is a moment in time when the Sun crosses the Earth's equator, which is to say, appears directly above the equator, rather than north or south of the equator. On the day of the equinox, the Sun appears to rise "due east" and set "due west". This occurs twice each year, around 20 March and 23 September.
A solstice is an event that occurs when the Sun reaches its most northerly or southerly excursion relative to the celestial equator on the celestial sphere. Two solstices occur annually, around June 21 and December 21. In many countries, the seasons of the year are determined by the solstices and the equinoxes.

A year is the time taken for astronomical objects to complete one orbit. For example, a year on Earth is the time taken for Earth to revolve around the Sun. Generally, a year is taken to mean a calendar year, but the word is also used for periods loosely associated with the calendar or astronomical year, such as the seasonal year, the fiscal year, the academic year, etc. The term can also be used in reference to any long period or cycle, such as the Great Year.

The zodiac is a belt-shaped region of the sky that extends approximately 8° north and south of the ecliptic, the apparent path of the Sun across the celestial sphere over the course of the year. Also within this zodiac belt appear the Moon and the brightest planets, along the their orbital planes. The zodiac is divided along the ecliptic into 12 equal parts ("signs"), each occupying 30° of celestial longitude. These signs roughly correspond to the astronomical constellations with the following modern names: Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Sagittarius, Capricorn, Aquarius, and Pisces.
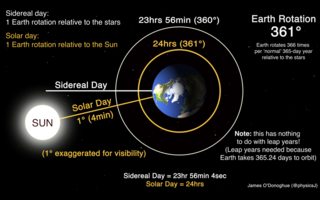
Sidereal time is a system of timekeeping used especially by astronomers. Using sidereal time and the celestial coordinate system, it is easy to locate the positions of celestial objects in the night sky. Sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars".
A sidereal year, also called a sidereal orbital period, is the time that Earth or another planetary body takes to orbit the Sun once with respect to the fixed stars.

In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism. In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years. This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—nutation and polar motion—are much smaller in magnitude.
A solar calendar is a calendar whose dates indicate the season or almost equivalently the apparent position of the Sun relative to the stars. The Gregorian calendar, widely accepted as a standard in the world, is an example of a solar calendar. The main other types of calendar are lunar calendar and lunisolar calendar, whose months correspond to cycles of Moon phases. The months of the Gregorian calendar do not correspond to cycles of the Moon phase.
The heliacal rising of a star or a planet occurs annually when it first becomes visible above the eastern horizon at dawn just before sunrise after a complete orbit of the Earth around the Sun. Historically, the most important such rising is that of Sirius, which was an important feature of the Egyptian calendar and astronomical development. The rising of the Pleiades heralded the start of the Ancient Greek sailing season, using celestial navigation, as well as the farming season. Helical rising is one of several types of risings and settings, mostly they are grouped into morning and evening risings and settings of objects in the sky. Culmination in the evening and then morning is set apart by half a year, while on the other hand risings and settings in the evenings and the mornings are only at the equator set apart by half a year.
In astronomy, an epoch or reference epoch is a moment in time used as a reference point for some time-varying astronomical quantity. It is useful for the celestial coordinates or orbital elements of a celestial body, as they are subject to perturbations and vary with time. These time-varying astronomical quantities might include, for example, the mean longitude or mean anomaly of a body, the node of its orbit relative to a reference plane, the direction of the apogee or aphelion of its orbit, or the size of the major axis of its orbit.
The Hindu calendar, also called Panchanga, is one of various lunisolar calendars that are traditionally used in the Indian subcontinent and Southeast Asia, with further regional variations for social and Hindu religious purposes. They adopt a similar underlying concept for timekeeping based on sidereal year for solar cycle and adjustment of lunar cycles in every three years, but differ in their relative emphasis to moon cycle or the sun cycle and the names of months and when they consider the New Year to start. Of the various regional calendars, the most studied and known Hindu calendars are the Shalivahana Shaka found in the Deccan region of Southern India and the Vikram Samvat (Bikrami) found in Nepal and the North and Central regions of India – both of which emphasize the lunar cycle. Their new year starts in spring. In regions such as Tamil Nadu and Kerala, the solar cycle is emphasized and this is called the Tamil calendar and Malayalam calendar and these have origins in the second half of the 1st millennium CE. A Hindu calendar is sometimes referred to as Panchangam (पञ्चाङ्गम्), which is also known as Panjika in Eastern India.

In astrology, sidereal and tropical are terms that refer to two different systems of ecliptic coordinates used to divide the ecliptic into twelve "signs". Each sign is divided into 30 degrees, making a total of 360 degrees. The terms sidereal and tropical may also refer to two different definitions of a year, applied in sidereal solar calendars or tropical solar calendars.
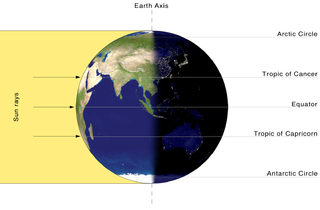
The March equinox or northward equinox is the equinox on the Earth when the subsolar point appears to leave the Southern Hemisphere and cross the celestial equator, heading northward as seen from Earth. The March equinox is known as the vernal equinox in the Northern Hemisphere and as the autumnal equinox in the Southern Hemisphere.
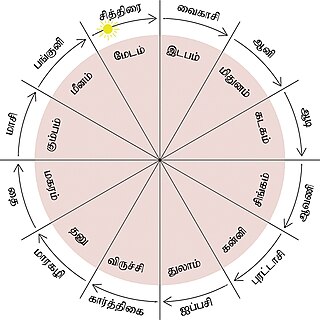
The Tamil calendar is a sidereal solar calendar used by the Tamil people of the Indian subcontinent. It is also used in Puducherry, and by the Tamil population in Sri Lanka, Malaysia, Singapore, and Mauritius.
The term Uttarāyaṇa is derived from two different Sanskrit words – "uttaram" (North) and "ayanam" (movement) – thus indicating the northward movement of the Sun. In the Gregorian calendar, this pertains to the "actual movement of the sun with respect to the earth." Also known as the six month period that occurs between the winter solstice and summer solstice. According to the Indian solar calendar, it refers to the movement of the Sun through the zodiac. This difference is because the solstices continually precess at a rate of 50 arcseconds per year due to the precession of the equinoxes, i.e. this difference is the difference between the sidereal and tropical zodiacs. The Surya Siddhanta bridges this difference by juxtaposing the four solstitial and equinoctial points with four of the twelve boundaries of the rashis.

The Moon orbits Earth in the prograde direction and completes one revolution relative to the Vernal Equinox and the stars in about 27.32 days and one revolution relative to the Sun in about 29.53 days. Earth and the Moon orbit about their barycentre, which lies about 4,670 km (2,900 mi) from Earth's centre, forming a satellite system called the Earth–Moon system. On average, the distance to the Moon is about 385,000 km (239,000 mi) from Earth's centre, which corresponds to about 60 Earth radii or 1.282 light-seconds.
A tropical year or solar year is the time that the Sun takes to return to the same position in the sky – as viewed from the Earth or another celestial body of the Solar System – thus completing a full cycle of astronomical seasons. For example, it is the time from vernal equinox to the next vernal equinox, or from summer solstice to the next summer solstice. It is the type of year used by tropical solar calendars.

In lunar calendars, a lunar month is the time between two successive syzygies of the same type: new moons or full moons. The precise definition varies, especially for the beginning of the month.
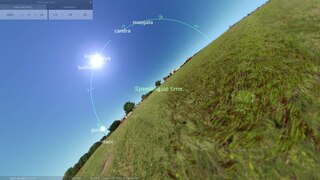
The Hindu calendar is based on a geocentric model of the Solar System. A geocentric model describes the Solar System as seen by an observer on the surface of the Earth.
References
- 1 2 Govt of India (1955). Report of the calendar reform committee. New Delhi: Council of Scientific and Industrial Reseaarch. p. 259. Retrieved 30 December 2023.
- ↑ Article titled "Precession of the Equinoxes" and authored by K. V. Sarma in: Helaine Selin (2008). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer. pp. 1830–1831. ISBN 978-1-4020-4559-2.
- ↑ S. K. Chatterjee (2004). "Uniform all-India nirayan solar calendar" (PDF). Indian Journal of History of Science. 39 (4): 519–514. Retrieved 31 December 2023.
- 1 2 3 "Indian calendars" (PDF). www.packolkata.gov.in. Positional Astronomy Center. Retrieved 31 December 2023.
- ↑ Robert Sewell (1896). The Indian Calendar. London: Swan Sonnenschein & Co. p. 10. Retrieved 1 January 2024.
- ↑ S.K. Uma, Padmaja Venugopal, K. Rupa and S. Balachandra Rao (2018). "The solar ingress according to makarandasarini and other Indian astronomical texts" (PDF). Journal of Astronomical History and Heritage. 21 (2): 202–210. Retrieved 1 January 2024.
{{cite journal}}: CS1 maint: multiple names: authors list (link)