Three-body problem

The accessibility of this article is in question. Relevant discussion may be found on the talk page. (June 2024)

In physics, specifically classical mechanics, the three-body problem is to take the initial positions and velocities (or momenta) of three point masses that orbit each other in space and calculate their subsequent trajectories using Newton's laws of motion and Newton's law of universal gravitation. ^[1]

Contents

• Mathematical description
• Restricted three-body problem
• Solutions
• General solution
• Special-case solutions
• Numerical approaches
• History
• Other problems involving three bodies
• n-body problem
• See also
• References
• Further reading
• External links

Unlike the two-body problem, the three-body problem has no general closed-form solution, meaning there is no equation that always solves it. ^[1] When three bodies orbit each other, the resulting dynamical system is chaotic for most initial conditions. Because there are no solvable equations for most three-body systems, the only way to predict the motions of the bodies is to estimate them using numerical methods.

The three-body problem is a special case of the n-body problem. Historically, the first specific three-body problem to receive extended study was the one involving the Earth, the Moon, and the Sun. ^[2] In an extended modern sense, a three-body problem is any problem in classical mechanics or quantum mechanics that models the motion of three particles.

Mathematical description

The mathematical statement of the three-body problem can be given in terms of the Newtonian equations of motion for vector positions ${\displaystyle \mathbf {r_{i}} =(x_{i},y_{i},z_{i})}$ of three gravitationally interacting bodies with masses ${\displaystyle m_{i}}$:

$${\displaystyle {\begin{aligned}{\ddot {\mathbf {r} }}_{\mathbf {1} }&=-Gm_{2}{\frac {\mathbf {r_{1}} -\mathbf {r_{2}} }{|\mathbf {r_{1}} -\mathbf {r_{2}} |^{3}}}-Gm_{3}{\frac {\mathbf {r_{1}} -\mathbf {r_{3}} }{|\mathbf {r_{1}} -\mathbf {r_{3}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {2} }&=-Gm_{3}{\frac {\mathbf {r_{2}} -\mathbf {r_{3}} }{|\mathbf {r_{2}} -\mathbf {r_{3}} |^{3}}}-Gm_{1}{\frac {\mathbf {r_{2}} -\mathbf {r_{1}} }{|\mathbf {r_{2}} -\mathbf {r_{1}} |^{3}}},\\{\ddot {\mathbf {r} }}_{\mathbf {3} }&=-Gm_{1}{\frac {\mathbf {r_{3}} -\mathbf {r_{1}} }{|\mathbf {r_{3}} -\mathbf {r_{1}} |^{3}}}-Gm_{2}{\frac {\mathbf {r_{3}} -\mathbf {r_{2}} }{|\mathbf {r_{3}} -\mathbf {r_{2}} |^{3}}}.\end{aligned}}}$$where ${\displaystyle G}$ is the gravitational constant. As astronomer Juhan Frank describes, "These three second-order vector differential equations are equivalent to 18 first order scalar differential equations." ^{[3] [ better source needed ]} As June Barrow-Green notes with regard to an alternative presentation, if

${\displaystyle P_{i}}$ represent three particles with masses ${\displaystyle m_{i}}$, distances ${\displaystyle P_{i}}$${\displaystyle P_{j}}$ = ${\displaystyle r_{ij}}$, and coordinates ${\displaystyle q_{ij}}$ (i,j = 1,2,3) in an inertial coordinate system ... the problem is described by nine second-order differential equations. ^{[4] : 8}

The problem can also be stated equivalently in the Hamiltonian formalism, in which case it is described by a set of 18 first-order differential equations, one for each component of the positions ${\displaystyle \mathbf {r_{i}} }$ and momenta ${\displaystyle \mathbf {p_{i}} }$:^{[ citation needed ] [5]}

$${\displaystyle {\frac {d\mathbf {r_{i}} }{dt}}={\frac {\partial {\mathcal {H}}}{\partial \mathbf {p_{i}} }},\qquad {\frac {d\mathbf {p_{i}} }{dt}}=-{\frac {\partial {\mathcal {H}}}{\partial \mathbf {r_{i}} }},}$$

where ${\displaystyle {\mathcal {H}}}$ is the Hamiltonian:^{[ citation needed ]}

$${\displaystyle {\mathcal {H}}=-{\frac {Gm_{1}m_{2}}{|\mathbf {r_{1}} -\mathbf {r_{2}} |}}-{\frac {Gm_{2}m_{3}}{|\mathbf {r_{3}} -\mathbf {r_{2}} |}}-{\frac {Gm_{3}m_{1}}{|\mathbf {r_{3}} -\mathbf {r_{1}} |}}+{\frac {\mathbf {p_{1}} ^{2}}{2m_{1}}}+{\frac {\mathbf {p_{2}} ^{2}}{2m_{2}}}+{\frac {\mathbf {p_{3}} ^{2}}{2m_{3}}}.}$$

In this case, ${\displaystyle {\mathcal {H}}}$ is simply the total energy of the system, gravitational plus kinetic.^{[ citation needed ]}

Restricted three-body problem

This section needs additional citations for verification . Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed.(July 2023) ( Learn how and when to remove this message )

In the restricted three-body problem formulation, in the description of Barrow-Green, ^{[4] : 11–14}

two... bodies revolve around their centre of mass in circular orbits under the influence of their mutual gravitational attraction, and... form a two body system... [whose] motion is known. A third body (generally known as a planetoid), assumed massless with respect to the other two, moves in the plane defined by the two revolving bodies and, while being gravitationally influenced by them, exerts no influence of its own. ^{[4] : 11}

Per Barrow-Green, "[t]he problem is then to ascertain the motion of the third body." ^{[4] : 11}

That is to say, this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.^{[ clarification needed ]} (That is, it is useful to consider the effective potential.^{[ clarification needed ][ according to whom? ]}) With respect to a rotating reference frame, the two co-orbiting bodies are stationary, and the third can be stationary as well at the Lagrangian points, or move around them, for instance on a horseshoe orbit.^{[ citation needed ]}

The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem. ^[6]

Mathematically, the problem is stated as follows.^{[ citation needed ]} Let ${\displaystyle m_{1,2}}$ be the masses of the two massive bodies, with (planar) coordinates ${\displaystyle (x_{1},y_{1})}$ and ${\displaystyle (x_{2},y_{2})}$, and let ${\displaystyle (x,y)}$ be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to ${\displaystyle 1}$. Then, the motion of the planetoid is given by:^{[ citation needed ]}

$${\displaystyle {\begin{aligned}{\frac {d^{2}x}{dt^{2}}}=-m_{1}{\frac {x-x_{1}}{r_{1}^{3}}}-m_{2}{\frac {x-x_{2}}{r_{2}^{3}}},\\{\frac {d^{2}y}{dt^{2}}}=-m_{1}{\frac {y-y_{1}}{r_{1}^{3}}}-m_{2}{\frac {y-y_{2}}{r_{2}^{3}}},\end{aligned}}}$$

where ${\displaystyle r_{i}={\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}}}}$.^{[ citation needed ]} In this form the equations of motion carry an explicit time dependence through the coordinates ${\displaystyle x_{i}(t),y_{i}(t)}$;^{[ citation needed ]} however, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.^{[ original research? ] [7]}

Solutions

General solution

There is no general closed-form solution to the three-body problem. ^[1] In other words, it does not have a general solution that can be expressed in terms of a finite number of standard mathematical operations. Moreover, the motion of three bodies is generally non-repeating, except in special cases. ^[8]

However, in 1912 the Finnish mathematician Karl Fritiof Sundman proved that there exists an analytic solution to the three-body problem in the form of a Puiseux series, specifically a power series in terms of powers of t^1/3. ^[9] This series converges for all real t, except for initial conditions corresponding to zero angular momentum. In practice, the latter restriction is insignificant since initial conditions with zero angular momentum are rare, having Lebesgue measure zero.

An important issue in proving this result is the fact that the radius of convergence for this series is determined by the distance to the nearest singularity. Therefore, it is necessary to study the possible singularities of the three-body problems. As is briefly discussed below, the only singularities in the three-body problem are binary collisions (collisions between two particles at an instant) and triple collisions (collisions between three particles at an instant).

Collisions of any number are somewhat improbable, since it has been shown that they correspond to a set of initial conditions of measure zero. But there is no criterion known to be put on the initial state in order to avoid collisions for the corresponding solution. So Sundman's strategy consisted of the following steps:

1. Using an appropriate change of variables to continue analyzing the solution beyond the binary collision, in a process known as regularization.
2. Proving that triple collisions only occur when the angular momentum L vanishes. By restricting the initial data to L ≠ 0, he removed all real singularities from the transformed equations for the three-body problem.
3. Showing that if L ≠ 0, then not only can there be no triple collision, but the system is strictly bounded away from a triple collision. This implies, by Cauchy's existence theorem for differential equations, that there are no complex singularities in a strip (depending on the value of L) in the complex plane centered around the real axis (related to the Cauchy–Kovalevskaya theorem).
4. Find a conformal transformation that maps this strip into the unit disc. For example, if s = t^1/3 (the new variable after the regularization) and if |ln s| ≤ β,^{[ clarification needed ]} then this map is given by $${\displaystyle \sigma ={\frac {e^{\frac {\pi s}{2\beta }}-1}{e^{\frac {\pi s}{2\beta }}+1}}.}$$

This finishes the proof of Sundman's theorem.

The corresponding series converges extremely slowly. That is, obtaining a value of meaningful precision requires so many terms that this solution is of little practical use. Indeed, in 1930, David Beloriszky calculated that if Sundman's series were to be used for astronomical observations, then the computations would involve at least 10^8000000 terms. ^[10]

Special-case solutions

In 1767, Leonhard Euler found three families of periodic solutions in which the three masses are collinear at each instant.

In 1772, Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. Together with Euler's collinear solutions, these solutions form the central configurations for the three-body problem. These solutions are valid for any mass ratios, and the masses move on Keplerian ellipses. These four families are the only known solutions for which there are explicit analytic formulae. In the special case of the circular restricted three-body problem, these solutions, viewed in a frame rotating with the primaries, become points called Lagrangian points and labeled L₁, L₂, L₃, L₄, and L₅, with L₄ and L₅ being symmetric instances of Lagrange's solution.

In work summarized in 1892–1899, Henri Poincaré established the existence of an infinite number of periodic solutions to the restricted three-body problem, together with techniques for continuing these solutions into the general three-body problem.

In 1893, Meissel stated what is now called the Pythagorean three-body problem: three masses in the ratio 3:4:5 are placed at rest at the vertices of a 3:4:5 right triangle, with the heaviest body at the right angle and the lightest at the smaller acute angle. Burrau ^[11] further investigated this problem in 1913. In 1967 Victor Szebehely and C. Frederick Peters established eventual escape of the lightest body for this problem using numerical integration, while at the same time finding a nearby periodic solution. ^[12]

In the 1970s, Michel Hénon and Roger A. Broucke each found a set of solutions that form part of the same family of solutions: the Broucke–Hénon–Hadjidemetriou family. In this family, the three objects all have the same mass and can exhibit both retrograde and direct forms. In some of Broucke's solutions, two of the bodies follow the same path. ^[14]

In 1993, physicist Cris Moore at the Santa Fe Institute found a zero angular momentum solution with three equal masses moving around a figure-eight shape. ^[15] In 2000, mathematicians Alain Chenciner and Richard Montgomery proved its formal existence. ^{[16] [17]} The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible for such orbits to be observed in the physical universe. But it has been argued that this is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event^{[ clarification needed ]} resulting in a figure-8 orbit has been estimated to be a small fraction of a percent. ^[18]

In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem. ^{[8] [14]}

In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem. ^[19]

In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem. ^[20] This was followed in 2018 by an additional 1,223 new solutions for a zero-angular-momentum system of unequal masses. ^[21]

In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three-body problem. ^[22] The free-fall formulation starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forward and backward along an open "track".

In 2023, Ivan Hristov, Radoslava Hristova, Dmitrašinović and Kiyotaka Tanikawa published a search for "periodic free-fall orbits" three-body problem, limited to the equal-mass case, and found 12,409 distinct solutions. ^[23]

History

The gravitational problem of three bodies in its traditional sense dates in substance from 1687, when Isaac Newton published his Philosophiæ Naturalis Principia Mathematica, in which Newton attempted to figure out if any long term stability is possible especially for such a system like that of our Earth, the Moon, and the Sun. Guided by major Renaissance astronomers Nicolaus Copernicus, Tycho Brahe and Johannes Kepler he introduced later generations to the beginning of the gravitational three-body problem. ^[27] In Proposition 66 of Book 1 of the Principia, and its 22 Corollaries, Newton took the first steps in the definition and study of the problem of the movements of three massive bodies subject to their mutually perturbing gravitational attractions. In Propositions 25 to 35 of Book 3, Newton also took the first steps in applying his results of Proposition 66 to the lunar theory, the motion of the Moon under the gravitational influence of Earth and the Sun. ^[28] Later, this problem was also applied to other planets' interactions with the Earth and the Sun. ^[27]

The physical problem was first addressed by Amerigo Vespucci and subsequently by Galileo Galilei, as well as Simon Stevin, but they did not realize what they contributed. Though Galileo determined that the speed of fall of all bodies changes uniformly and in the same way, he did not apply it to planetary motions. ^[27] Whereas in 1499, Vespucci used knowledge of the position of the Moon to determine his position in Brazil. ^[29] It became of technical importance in the 1720s, as an accurate solution would be applicable to navigation, specifically for the determination of longitude at sea, solved in practice by John Harrison's invention of the marine chronometer. However the accuracy of the lunar theory was low, due to the perturbing effect of the Sun and planets on the motion of the Moon around Earth.

Jean le Rond d'Alembert and Alexis Clairaut, who developed a longstanding rivalry, both attempted to analyze the problem in some degree of generality; they submitted their competing first analyses to the Académie Royale des Sciences in 1747. ^[30] It was in connection with their research, in Paris during the 1740s, that the name "three-body problem" (French : Problème des trois Corps) began to be commonly used. An account published in 1761 by Jean le Rond d'Alembert indicates that the name was first used in 1747. ^[31]

From the end of the 19th century to early 20th century, the approach to solve the three-body problem with the usage of short-range attractive two-body forces was developed by scientists, which offered P.F. Bedaque, H.-W. Hammer and U. van Kolck an idea to renormalize the short-range three-body problem, providing scientists a rare example of a renormalization group limit cycle at the beginning of the 21st century. ^[32] George William Hill worked on the restricted problem in the late 19th century with an application of motion of Venus and Mercury. ^[33]

At the beginning of the 20th century, Karl Sundman approached the problem mathematically and systematically by providing a functional theoretical proof to the problem valid for all values of time. It was the first time scientists theoretically solved the three-body problem. However, because there was not a qualitative enough solution of this system, and it was too slow for scientists to practically apply it, this solution still left some issues unresolved. ^[34] In the 1970s, implication to three-body from two-body forces had been discovered by V. Efimov, which was named the Efimov effect. ^[35]

In 2017, Shijun Liao and Xiaoming Li applied a new strategy of numerical simulation for chaotic systems called the clean numerical simulation (CNS), with the use of a national supercomputer, to successfully gain 695 families of periodic solutions of the three-body system with equal mass. ^[36]

In 2019, Breen et al. announced a fast neural network solver for the three-body problem, trained using a numerical integrator. ^[37]

In September 2023, several possible solutions have been found to the problem according to reports. ^{[38] [39]}

Other problems involving three bodies

The term "three-body problem" is sometimes used in the more general sense to refer to any physical problem involving the interaction of three bodies.

A quantum-mechanical analogue of the gravitational three-body problem in classical mechanics is the helium atom, in which a helium nucleus and two electrons interact according to the inverse-square Coulomb interaction. Like the gravitational three-body problem, the helium atom cannot be solved exactly. ^[40]

In both classical and quantum mechanics, however, there exist nontrivial interaction laws besides the inverse-square force that do lead to exact analytic three-body solutions. One such model consists of a combination of harmonic attraction and a repulsive inverse-cube force. ^[41] This model is considered nontrivial since it is associated with a set of nonlinear differential equations containing singularities (compared with, e.g., harmonic interactions alone, which lead to an easily solved system of linear differential equations). In these two respects it is analogous to (insoluble) models having Coulomb interactions, and as a result has been suggested as a tool for intuitively understanding physical systems like the helium atom. ^{[41] [42]}

Within the point vortex model, the motion of vortices in a two-dimensional ideal fluid is described by equations of motion that contain only first-order time derivatives. I.e. in contrast to Newtonian mechanics, it is the velocity and not the acceleration that is determined by their relative positions. As a consequence, the three-vortex problem is still integrable, ^[43] while at least four vortices are required to obtain chaotic behavior. ^[44] One can draw parallels between the motion of a passive tracer particle in the velocity field of three vortices and the restricted three-body problem of Newtonian mechanics. ^[45]

The gravitational three-body problem has also been studied using general relativity. Physically, a relativistic treatment becomes necessary in systems with very strong gravitational fields, such as near the event horizon of a black hole. However, the relativistic problem is considerably more difficult than in Newtonian mechanics, and sophisticated numerical techniques are required. Even the full two-body problem (i.e. for arbitrary ratio of masses) does not have a rigorous analytic solution in general relativity. ^[46]

n-body problem

The three-body problem is a special case of the n-body problem, which describes how n objects move under one of the physical forces, such as gravity. These problems have a global analytical solution in the form of a convergent power series, as was proven by Karl F. Sundman for n = 3 and by Qiudong Wang for n > 3 (see n-body problem for details). However, the Sundman and Wang series converge so slowly that they are useless for practical purposes; ^[47] therefore, it is currently necessary to approximate solutions by numerical analysis in the form of numerical integration or, for some cases, classical trigonometric series approximations (see n-body simulation). Atomic systems, e.g. atoms, ions, and molecules, can be treated in terms of the quantum n-body problem. Among classical physical systems, the n-body problem usually refers to a galaxy or to a cluster of galaxies; planetary systems, such as stars, planets, and their satellites, can also be treated as n-body systems. Some applications are conveniently treated by perturbation theory, in which the system is considered as a two-body problem plus additional forces causing deviations from a hypothetical unperturbed two-body trajectory.

See also

Related Research Articles

Angular momentum is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, flying discs, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it.

In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:

1. A body remains at rest, or in motion at a constant speed in a straight line, except insofar as it is acted upon by a force.
2. At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time.
3. If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.

The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

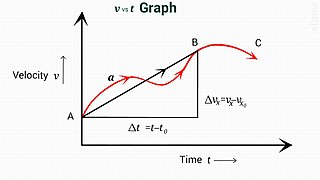
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.

In classical mechanics, free fall is any motion of a body where gravity is the only force acting upon it. A freely falling object may not necessarily be falling down in the vertical direction. An object moving upwards might not normally be considered to be falling, but if it is subject to only the force of gravity, it is said to be in free fall. The Moon is thus in free fall around the Earth, though its orbital speed keeps it in very far orbit from the Earth's surface.

In physics, the center of mass of a distribution of mass in space is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. For a rigid body containing its center of mass, this is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.

Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.

In classical mechanics, the two-body problem is to calculate and predict the motion of two massive bodies that are orbiting each other in space. The problem assumes that the two bodies are point particles that interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored.

In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1. They are frequently used during various astrodynamic calculations.

In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body.

In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space. It is a particular version of the three-body problem. This version of is exactly solvable, and yields an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler, who discussed it in memoirs published in 1760. Important extensions and analyses to the three body problem were contributed subsequently by Joseph-Louis Lagrange, Joseph Liouville, Pierre-Simon Laplace, Carl Gustav Jacob Jacobi, Urbain Le Verrier, William Rowan Hamilton, Henri Poincaré and George David Birkhoff, among others. The Euler three-body problem is known by a variety of names, such as the problem of two fixed centers, the Euler–Jacobi problem, and the two-center Kepler problem. The exact solution, in the full three dimensional case, can be expressed in terms of Weierstrass's elliptic functions For convenience, the problem may also be solved by numerical methods, such as Runge–Kutta integration of the equations of motion. The total energy of the moving particle is conserved, but its linear and angular momentum are not, since the two fixed centers can apply a net force and torque. Nevertheless, the particle has a second conserved quantity that corresponds to the angular momentum or to the Laplace–Runge–Lenz vector as limiting cases.

The Schrödinger–Newton equation, sometimes referred to as the Newton–Schrödinger or Schrödinger–Poisson equation, is a nonlinear modification of the Schrödinger equation with a Newtonian gravitational potential, where the gravitational potential emerges from the treatment of the wave function as a mass density, including a term that represents interaction of a particle with its own gravitational field. The inclusion of a self-interaction term represents a fundamental alteration of quantum mechanics. It can be written either as a single integro-differential equation or as a coupled system of a Schrödinger and a Poisson equation. In the latter case it is also referred to in the plural form.

In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force that varies in strength as the inverse square of the distance between them. The force may be either attractive or repulsive. The problem is to find the position or speed of the two bodies over time given their masses, positions, and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements.

The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation.

In classical mechanics, Appell's equation of motion is an alternative general formulation of classical mechanics described by Josiah Willard Gibbs in 1879 and Paul Émile Appell in 1900.

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.

In physics, the n-body problem is the problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem has been motivated by the desire to understand the motions of the Sun, Moon, planets, and visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem. The n-body problem in general relativity is considerably more difficult to solve due to additional factors like time and space distortions.

In classical mechanics, the central-force problem is to determine the motion of a particle in a single central potential field. A central force is a force that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In a few important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.

References

Further reading

This "Further reading" section may need cleanup. Please read the editing guide and help improve the section.(June 2024) ( Learn how and when to remove this message )

External links

• Chenciner, Alain (2007). "Three body problem". Scholarpedia . 2 (10): 2111. Bibcode:2007SchpJ...2.2111C. doi: 10.4249/scholarpedia.2111 .
• The '3-body problem' may not be so chaotic after all, new study suggests (Live Science, October 22, 2024)
• Physicists Discover a Whopping 13 New Solutions to Three-Body Problem (Science, March 8, 2013)
• 3body simulator Archived 2022-11-17 at the Wayback Machine – an example of a computer program that solves the three-body problem numerically