Horseshoe map

Last updated December 12, 2023

In the mathematics of chaos theory, a horseshoe map is any member of a class of chaotic maps of the square into itself. It is a core example in the study of dynamical systems. The map was introduced by Stephen Smale while studying the behavior of the orbits of the van der Pol oscillator. The action of the map is defined geometrically by squishing the square, then stretching the result into a long strip, and finally folding the strip into the shape of a horseshoe.

Most points eventually leave the square under the action of the map. They go to the side caps where they will, under iteration, converge to a fixed point in one of the caps. The points that remain in the square under repeated iteration form a fractal set and are part of the invariant set of the map.

The squishing, stretching and folding of the horseshoe map are typical of chaotic systems, but not necessary or even sufficient.^[1]

In the horseshoe map, the squeezing and stretching are uniform. They compensate each other so that the area of the square does not change. The folding is done neatly, so that the orbits that remain forever in the square can be simply described.

For a horseshoe map:

there are an infinite number of periodic orbits;
periodic orbits of arbitrarily long period exist;
the number of periodic orbits grows exponentially with the period; and
close to any point of the fractal invariant set there is a point of a periodic orbit.

The horseshoe map

The horseshoe map $f$ is a diffeomorphism defined from a region $S$ of the plane into itself. The region $S$ is a square capped by two semi-disks. The codomain of $f$ (the "horseshoe") is a proper subset of its domain $S$ . The action of $f$ is defined through the composition of three geometrically defined transformations. First the square is contracted along the vertical direction by a factor $a < .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2$ . The caps are contracted so as to remain semi-disks attached to the resulting rectangle. Contracting by a factor smaller than one half assures that there will be a gap between the branches of the horseshoe. Next the rectangle is stretched horizontally by a factor of $1 / a$ ; the caps remain unchanged. Finally the resulting strip is folded into a horseshoe-shape and placed back into $S$ .

The interesting part of the dynamics is the image of the square into itself. Once that part is defined, the map can be extended to a diffeomorphism by defining its action on the caps. The caps are made to contract and eventually map inside one of the caps (the left one in the figure). The extension of f to the caps adds a fixed point to the non-wandering set of the map. To keep the class of horseshoe maps simple, the curved region of the horseshoe should not map back into the square.

The horseshoe map is one-to-one, which means that an inverse f⁻¹ exists when restricted to the image of $S$ under $f$ .

By folding the contracted and stretched square in different ways, other types of horseshoe maps are possible.

Variants of the horseshoe map DifferentHS.svg — Variants of the horseshoe map

To ensure that the map remains one-to-one, the contracted square must not overlap itself. When the action on the square is extended to a diffeomorphism, the extension cannot always be done in the plane. For example, the map on the right needs to be extended to a diffeomorphism of the sphere by using a “cap” that wraps around the equator.

The horseshoe map is an Axiom A diffeomorphism that serves as a model for the general behavior at a transverse homoclinic point, where the stable and unstable manifolds of a periodic point intersect.

Dynamics of the map

The horseshoe map was designed to reproduce the chaotic dynamics of a flow in the neighborhood of a given periodic orbit. The neighborhood is chosen to be a small disk perpendicular to the orbit. As the system evolves, points in this disk remain close to the given periodic orbit, tracing out orbits that eventually intersect the disk once again. Other orbits diverge.

The behavior of all the orbits in the disk can be determined by considering what happens to the disk. The intersection of the disk with the given periodic orbit comes back to itself every period of the orbit and so do points in its neighborhood. When this neighborhood returns, its shape is transformed. Among the points back inside the disk are some points that will leave the disk neighborhood and others that will continue to return. The set of points that never leaves the neighborhood of the given periodic orbit form a fractal.

A symbolic name can be given to all the orbits that remain in the neighborhood. The initial neighborhood disk can be divided into a small number of regions. Knowing the sequence in which the orbit visits these regions allows the orbit to be pinpointed exactly. The visitation sequence of the orbits provide a symbolic representation of the dynamics, known as symbolic dynamics.

Orbits

It is possible to describe the behavior of all initial conditions of the horseshoe map. An initial point u₀ = (x, y) gets mapped into the point u₁ = f(u₀). Its iterate is the point u₂ = f(u₁) = f²(u₀), and repeated iteration generates the orbit u₀, u₁, u₂, ...

Under repeated iteration of the horseshoe map, most orbits end up at the fixed point in the left cap. This is because the horseshoe maps the left cap into itself by an affine transformation that has exactly one fixed point. Any orbit that lands on the left cap never leaves it and converges to the fixed point in the left cap under iteration. Points in the right cap get mapped into the left cap on the next iteration, and most points in the square get mapped into the caps. Under iteration, most points will be part of orbits that converge to the fixed point in the left cap, but some points of the square never leave.

Iterating the square

Pre-images of the square region Foldings2.png — Pre-images of the square region

Under forward iterations of the horseshoe map, the original square gets mapped into a series of horizontal strips. The points in these horizontal strips come from vertical strips in the original square. Let $S 0$ be the original square, map it forward n times, and consider only the points that fall back into the square $S 0$ , which is a set of horizontal stripes

H_{n}=f^{n}(S_{0})\cap S_{0}.

The points in the horizontal stripes came from the vertical stripes

V_{n}=f^{-n}(H_{n})

,

which are the horizontal strips $H n$ mapped backwards n times. That is, a point in $V n$ will, under n iterations of the horseshoe, end up in the set $H n$ of vertical strips.

Invariant set

Example of an invariant measure Ising-tartan.png — Example of an invariant measure

If a point is to remain indefinitely in the square, then it must belong to a set $Λ$ that maps to itself. Whether this set is empty or not has to be determined. The vertical strips $V 1$ map into the horizontal strips $H 1$ , but not all points of $V 1$ map back into $V 1$ . Only the points in the intersection of $V 1$ and $H 1$ may belong to $Λ$ , as can be checked by following points outside the intersection for one more iteration.

The intersection of the horizontal and vertical stripes, $H n \cap V n$ , are squares that in the limit $n \to \infty$ converge to the invariant set $Λ$ (this set is an intersection of a Cantor set of vertical lines with a Cantor set of horizontal lines^[2]). The structure of this set can be better understood by introducing a system of labels for all the intersections—a symbolic dynamics.

Symbolic dynamics

The basic domains of the horseshoe map HMstrips.svg — The basic domains of the horseshoe map

Since $H n \cap V n \subset V 1$ , any point that is in $Λ$ under iteration must land in the left vertical strip $A$ of $V 1$ , or on the right vertical strip $B$ . The lower horizontal strip of $H 1$ is the image of $A$ and the upper horizontal strip is the image of $B$ , so H₁ = f(A) ∪ f(B). The strips $A$ and $B$ can be used to label the four squares in the intersection of $V 1$ and $H 1$ :

{\begin{aligned}\Lambda _{A\bullet A}&=f(A)\cap A\\\Lambda _{A\bullet B}&=f(A)\cap B\\\Lambda _{B\bullet A}&=f(B)\cap A\\\Lambda _{B\bullet B}&=f(B)\cap B\end{aligned}}

The set $Λ B•A$ consist of points from strip $A$ that were in strip $B$ in the previous iteration. A dot is used to separate the region the point of an orbit is in from the region the point came from.

The notation can be extended to higher iterates of the horseshoe map. The vertical strips can be named according to the sequence of visits to strip $A$ or strip $B$ . For example, the set ABB ⊂ V₃ consists of the points from $A$ that will all land in $B$ in one iteration and remain in $B$ in the iteration after that:

ABB=\{x\in A\,|\,f(x)\in B\,\,\,\mathrm {and} \,\,\,f_{2}(x)\in B\}.

Working backwards from that trajectory determines a small region, the set ABB, within V₃.

The horizontal strips are named from their vertical strip pre-images. In this notation, the intersection of V₂ and H₂ consists of 16 squares, one of which is

\Lambda _{AB\bullet BB}=f_{2}(AB)\cap BB.

All the points in Λ_AB•BB are in $B$ and will continue to be in $B$ for at least one more iteration. Their previous trajectory before landing in BB was $A$ followed by $B$ .

Periodic orbits

Any one of the intersections $Λ P•F$ of a horizontal strip with a vertical strip, where P and F are sequences of As and Bs, is an affine transformation of a small region in V₁. If P has k symbols in it, and if $f - k (Λ P•F)$ and $Λ P•F$ intersect, the region $Λ P•F$ will have a fixed point. This happens when the sequence P is the same as F. For example, $Λ ABAB•ABAB \subset V 4 \cap H 4$ has at least one fixed point. This point is also the same as the fixed point in Λ_AB•AB. By including more and more ABs in the P and F part of the label of intersection, the area of the intersection can be made as small as needed. It converges to a point that is part of a periodic orbit of the horseshoe map. The periodic orbit can be labeled by the simplest sequence of $A$ s and $B$ s that labels one of the regions the periodic orbit visits.

For every sequence of $A$ s and $B$ s there is a periodic orbit.

Notes

↑ David Ruelle (2006). "What is a strange attractor?" (PDF). Notices of the American Mathematical Society. 53 (7): 764–765.
↑ Ott, Edward (2002). Chaos in Dynamical Systems (2nd ed.). Cambridge University Press.

Related Research Articles

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. Affine space is the setting for affine geometry.

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable and the parameters are complex numbers. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

In mathematics, an iterated function is a function $X \to X$ which is obtained by composing another function $f : X \to X$ with itself a certain number of times. The process of repeatedly applying the same function is called iteration. In this process, starting from some initial object, the result of applying a given function is fed again in the function as input, and this process is repeated. For example on the image on the right:

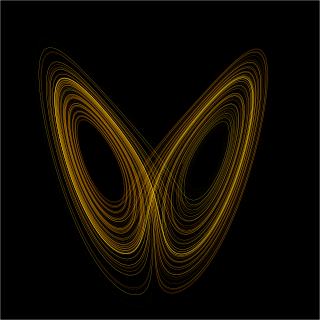
The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor. Rössler interpreted it as a formalization of a taffy-pulling machine.

<span class="mw-page-title-main">Cobweb plot</span>

A cobweb plot, or Verhulst diagram is a visual tool used in the dynamical systems field of mathematics to investigate the qualitative behaviour of one-dimensional iterated functions, such as the logistic map. Using a cobweb plot, it is possible to infer the long term status of an initial condition under repeated application of a map.

In mathematics, the tent map with parameter μ is the real-valued function f_μ defined by

<span class="mw-page-title-main">Bifurcation theory</span> Study of sudden qualitative behavior changes caused by small parameter changes

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems and discrete systems.

In dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some Riemannian metric on M. An analogous definition applies to the case of flows.

<span class="mw-page-title-main">Homoclinic orbit</span> Closed loop through a phase space

In the study of dynamical systems, a homoclinic orbit is a path through phase space which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium. It is a heteroclinic orbit–a path between any two equilibrium points–in which the endpoints are one and the same.

In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.

In mathematics, Smale's axiom A defines a class of dynamical systems which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale. The importance of such systems is demonstrated by the chaotic hypothesis, which states that, 'for all practical purposes', a many-body thermostatted system is approximated by an Anosov system.

<span class="mw-page-title-main">Arnold's cat map</span> Chaotic map from the torus into itself

In mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name.

In mathematics, the tricorn, sometimes called the Mandelbar set, is a fractal defined in a similar way to the Mandelbrot set, but using the mapping $instead of used for the Mandelbrot set. It was introduced by W. D. Crowe, R. Hasson, P. J. Rippon, and P. E. D. Strain-Clark. John Milnor found tricorn-like sets as a prototypical configuration in the parameter space of real cubic polynomials, and in various other families of rational maps.$

<span class="mw-page-title-main">Misiurewicz point</span> Parameter in the Mandelbrot set

In mathematics, a Misiurewicz point is a parameter value in the Mandelbrot set and also in real quadratic maps of the interval for which the critical point is strictly pre-periodic. By analogy, the term Misiurewicz point is also used for parameters in a multibrot set where the unique critical point is strictly pre-periodic. This term makes less sense for maps in greater generality that have more than one free critical point because some critical points might be periodic and others not. These points are named after the Polish-American mathematician Michał Misiurewicz, who was the first to study them.

Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations,

A complex quadratic polynomial is a quadratic polynomial whose coefficients and variable are complex numbers.

A Siegel disc or Siegel disk is a connected component in the Fatou set where the dynamics is analytically conjugate to an irrational rotation.

Fubini's nightmare is a seeming violation of Fubini's theorem, where a nice space, such as the square $is foliated by smooth fibers, but there exists a set of positive measure whose intersection with each fiber is singular. There is no real contradiction to Fubini's theorem because despite smoothness of the fibers, the foliation is not absolutely continuous, and neither are the conditional measures on fibers.$

References

David Ruelle (2006). "What is a strange attractor?" (PDF). Notices of the American Mathematical Society. 53 (7): 764–765.
Stephen Smale (1967). "Differentiable dynamical systems". Bulletin of the American Mathematical Society. 73 (6): 747–817. doi: 10.1090/S0002-9904-1967-11798-1 .
P. Cvitanović; G. Gunaratne; I. Procaccia (1988). "Topological and metric properties of Hénon-type strange attractors". Physical Review A. 38 (3): 1503–1520. Bibcode:1988PhRvA..38.1503C. doi:10.1103/PhysRevA.38.1503. PMID 9900529.
André de Carvalho (1999). "Pruning fronts and the formation of horseshoes". Ergodic Theory and Dynamical Systems. 19 (4): 851–894. arXiv: math/9701217 . doi:10.1017/S0143385799133972. S2CID 17153861.
André de Carvalho; Toby Hall (2002). "How to prune a horseshoe" (PDF). Nonlinearity. 15 (3): R19–R68. Bibcode:2002Nonli..15R..19D. doi:10.1088/0951-7715/15/3/201. S2CID 53417965. Archived from the original (PDF) on 2019-03-02.

External links

"Smale Horseshoe". Scholarpedia .
Evgeny Demidov (2007). "Homoclinic structures in the standard map". ibiblio.org. Retrieved 2016-07-11.
ChaosBook.org Chapter "Stretch, fold, prune"
CHAOS VI - Chaos and Horseshoe Chapter from Jos Leys, Étienne Ghys and Aurélien Alvarez movie Chaos
Richeson, David (2022-03-02). "How Mathematicians Make Sense of Chaos". Quanta Magazine .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] David Ruelle (2006). "What is a strange attractor?" (PDF). Notices of the American Mathematical Society. 53 (7): 764–765.

[2] Ott, Edward (2002). Chaos in Dynamical Systems (2nd ed.). Cambridge University Press.

[1]

[2]