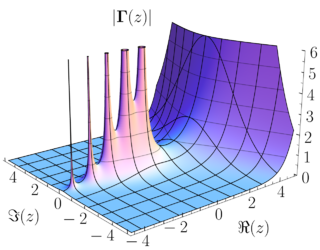
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if is holomorphic in a simply connected domain Ω, then for any simply closed contour in Ω, that contour integral is zero.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable. When the variable is time, they are also called time-invariant systems.
In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line, which may not intersect the generatrix. The surface created by this revolution and which bounds the solid is the surface of revolution.
A surface of revolution is a surface in Euclidean space created by rotating a curve one full revolution around an axis of rotation . The volume bounded by the surface created by this revolution is the solid of revolution.
Hilbert's 16th problem was posed by David Hilbert at the Paris conference of the International Congress of Mathematicians in 1900, as part of his list of 23 problems in mathematics.
In differential calculus, related rates problems involve finding a rate at which a quantity changes by relating that quantity to other quantities whose rates of change are known. The rate of change is usually with respect to time. Because science and engineering often relate quantities to each other, the methods of related rates have broad applications in these fields. Differentiation with respect to time or one of the other variables requires application of the chain rule, since most problems involve several variables.
The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor. Rössler interpreted it as a formalization of a taffy-pulling machine.
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue sky bifurcation in reference to the sudden creation of two fixed points.
In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where, as a parameter changes, a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis as a parameter crosses a threshold value. Under reasonably generic assumptions about the dynamical system, the fixed point becomes a small-amplitude limit cycle as the parameter changes.
Chua's circuit is a simple electronic circuit that exhibits classic chaotic behavior. This means roughly that it is a "nonperiodic oscillator"; it produces an oscillating waveform that, unlike an ordinary electronic oscillator, never "repeats". It was invented in 1983 by Leon O. Chua, who was a visitor at Waseda University in Japan at that time. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system, leading some to declare it "a paradigm for chaos".
The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. The term "butterfly effect" in popular media may stem from the real-world implications of the Lorenz attractor, namely that several different initial chaotic conditions evolve in phase space in a way that never repeats, so all chaos is unpredictable. This underscores that chaotic systems can be completely deterministic and yet still be inherently unpredictable over long periods of time. Because chaos continually increases in systems, it is impossible to predict the future of systems well. For instance, even the small flap of a butterfly's wings could set the world on a vastly different trajectory, such as by causing a hurricane. The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to resemble a butterfly.
The triple product rule, known variously as the cyclic chain rule, cyclic relation, cyclical rule or Euler's chain rule, is a formula which relates partial derivatives of three interdependent variables. The rule finds application in thermodynamics, where frequently three variables can be related by a function of the form f(x, y, z) = 0, so each variable is given as an implicit function of the other two variables. For example, an equation of state for a fluid relates temperature, pressure, and volume in this manner. The triple product rule for such interrelated variables x, y, and z comes from using a reciprocity relation on the result of the implicit function theorem, and is given by
In differential calculus, there is no single uniform notation for differentiation. Instead, various notations for the derivative of a function or variable have been proposed by various mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
The Hindmarsh–Rose model of neuronal activity is aimed to study the spiking-bursting behavior of the membrane potential observed in experiments made with a single neuron. The relevant variable is the membrane potential, x(t), which is written in dimensionless units. There are two more variables, y(t) and z(t), which take into account the transport of ions across the membrane through the ion channels. The transport of sodium and potassium ions is made through fast ion channels and its rate is measured by y(t), which is called the spiking variable. z(t) corresponds to an adaptation current, which is incremented at every spike, leading to a decrease in the firing rate. Then, the Hindmarsh–Rose model has the mathematical form of a system of three nonlinear ordinary differential equations on the dimensionless dynamical variables x(t), y(t), and z(t). They read:
In mathematics, the slow manifold of an equilibrium point of a dynamical system occurs as the most common example of a center manifold. One of the main methods of simplifying dynamical systems, is to reduce the dimension of the system to that of the slow manifold—center manifold theory rigorously justifies the modelling. For example, some global and regional models of the atmosphere or oceans resolve the so-called quasi-geostrophic flow dynamics on the slow manifold of the atmosphere/oceanic dynamics, and is thus crucial to forecasting with a climate model.
Guanrong Chen (陈关荣) or Ron Chen is a Chinese mathematician who made contributions to Chaos theory. He has been the chair professor and the founding director of the Centre for Chaos and Complex Networks at the City University of Hong Kong since 2000. Prior to that, he was a tenured full professor at the University of Houston, Texas. Chen was elected Member of the Academy of Europe in 2014, elected Fellow of The World Academy of Sciences in 2015, and elected IEEE Fellow in 1997. He is currently the editor-in-chief for the International Journal of Bifurcation and Chaos.
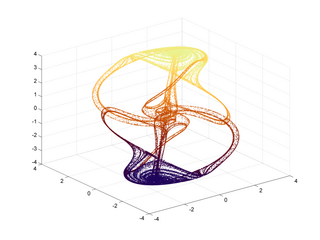
In the dynamical systems theory, Thomas' cyclically symmetric attractor is a 3D strange attractor originally proposed by René Thomas. It has a simple form which is cyclically symmetric in the x, y, and z variables and can be viewed as the trajectory of a frictionally dampened particle moving in a 3D lattice of forces. The simple form has made it a popular example.
In mathematics, Chrystal's equation is a first order nonlinear ordinary differential equation, named after the mathematician George Chrystal, who discussed the singular solution of this equation in 1896. The equation reads as
Chen attractor
parameters a = 35, c = 27, b = 2.8,x(0) = -.1, y(0) = .3, z(0) = -.6
Lu Chen attractor
Maple plot of N scroll attractor based on Chen with sine and tau
9 scroll modified Chua chaotic attractor
xy plot of 9 scroll modified Chua chaotic attractor
PWL Duffing chaotic attractor xy plot
PWL Duffing chaotic attractor plot
modified Lorenz attractor
Rabinovich Fabrikant attractor xy plot
