Outer billiards

Last updated

Outer billiards is a dynamical system based on a convex shape in the plane. Classically, this system is defined for the Euclidean plane [1] but one can also consider the system in the hyperbolic plane [2] or in other spaces that suitably generalize the plane. Outer billiards differs from a usual dynamical billiard in that it deals with a discrete sequence of moves outside the shape rather than inside of it.

Contents

Definitions

The outer billiards map

Let P be a convex shape in the plane. Given a point x0 outside P, there is typically a unique point x1 (also outside P) so that the line segment connecting x0 to x1 is tangent to P at its midpoint and a person walking from x0 to x1 would see P on the right. (See Figure.) The map F: x0 -> x1 is called the outer billiards map.

Outer billiards defined relative to a pentagon OuterBilliardsDefinition.png
Outer billiards defined relative to a pentagon

The inverse (or backwards) outer billiards map is also defined, as the map x1 -> x0. One gets the inverse map simply by replacing the word right by the word left in the definition given above. The figure shows the situation in the Euclidean plane, but the definition in the hyperbolic plane is essentially the same.

Orbits

An outer billiards orbit is the set of all iterations of the point, namely ... x0 ↔ x1 ↔ x2 ↔ x3 ... That is, start at x0 and iteratively apply both the outer billiards map and the backwards outer billiards map. When P is a strictly convex shape, such as an ellipse, every point in the exterior of P has a well defined orbit. When P is a polygon, some points might not have well-defined orbits, on account of the potential ambiguity of choosing the midpoint of the relevant tangent line. Nevertheless, in the polygonal case, almost every point has a well-defined orbit.

Higher-dimensional spaces

Defining an outer billiards system in a higher-dimensional space is beyond the scope of this article. Unlike the case of ordinary billiards, the definition is not straightforward. One natural setting for the map is a complex vector space. In this case, there is a natural choice of line tangent to a convex body at each point. One obtains these tangents by starting with the normals and using the complex structure to rotate 90 degrees. These distinguished tangent lines can be used to define the outer billiards map roughly as above. [1]

History

Most people attribute the introduction of outer billiards to Bernhard Neumann in the late 1950s, [3] though it seems that a few people cite an earlier construction in 1945, due to M. Day. Jürgen Moser popularized the system in the 1970s as a toy model for celestial mechanics. [4] [5] This system has been studied classically in the Euclidean plane, and more recently in the hyperbolic plane. One can also consider higher-dimensional spaces, though no serious study has yet been made. Bernhard Neumann informally posed the question as to whether or not one can have unbounded orbits in an outer billiards system, and Moser put it in writing in 1973. [4] Sometimes this basic question has been called the Moser-Neumann question. This question, originally posed for shapes in the Euclidean plane and solved only recently, has been a guiding problem in the field.

Moser-Neumann question

Bounded orbits in the Euclidean plane

In the 70's, Jürgen Moser sketched a proof, based on K.A.M. theory, that outer billiards relative to a 6-times-differentiable shape of positive curvature has all orbits bounded. In 1982, Raphael Douady gave the full proof of this result. [6] A big advance in the polygonal case came over a period of several years when three teams of authors, Vivaldi-Shaidenko, [7] Kolodziej, [8] and Gutkin-Simanyi, [9] each using different methods, showed that outer billiards relative to a quasirational polygon has all orbits bounded. The notion of quasirational is technical (see references) but it includes the class of regular polygons and convex rational polygons, namely those convex polygons whose vertices have rational coordinates. In the case of rational polygons, all the orbits are periodic. In 1995, Sergei Tabachnikov showed that outer billiards for the regular pentagon has some aperiodic orbits, thus clarifying the distinction between the dynamics in the rational and regular cases. [1] In 1996, Philip Boyland showed that outer billiards relative to some shapes can have orbits which accumulate on the shape. [10] In 2005, Daniel Genin showed that all orbits are bounded when the shape is a trapezoid, thus showing that quasirationality is not a necessary condition for the system to have all orbits bounded. [11] (Not all trapezoids are quasirational.)

Unbounded orbits in the Euclidean plane

In 2007, Richard Schwartz showed that outer billiards has some unbounded orbits when defined relative to the Penrose Kite, thus answering the original Moser-Neumann question in the affirmative. [12] The Penrose kite is the convex quadrilateral from the kites-and-darts Penrose tilings. Subsequently, Schwartz showed that outer billiards has unbounded orbits when defined relative to any irrational kite. [13] An irrational kite is a quadrilateral with the following property: One of the diagonals of the quadrilateral divides the region into two triangles of equal area and the other diagonal divides the region into two triangles whose areas are not rational multiples of each other. In 2008, Dmitry Dolgopyat and Bassam Fayad showed that outer billiards defined relative to the semidisk has unbounded orbits. [14] The semidisk is the region one gets by cutting a disk in half. The proof of Dolgopyat-Fayad is robust, and also works for regions obtained by cutting a disk nearly in half, when the word nearly is suitably interpreted.

Unbounded orbits in the hyperbolic plane

In 2003, Filiz Doǧru and Sergei Tabachnikov showed that all orbits are unbounded for a certain class of convex polygons in the hyperbolic plane. [15] The authors call such polygons large. (See the reference for the definition.) Filiz Doǧru and Samuel Otten then extended this work in 2011 by specifying the conditions under which a regular polygonal table in the hyperbolic plane have all orbits unbounded, that is, are large. [16]

Existence of periodic orbits

In ordinary polygonal billiards, the existence of periodic orbits is a major unsolved problem. For instance, it is unknown if every triangular shaped table has a periodic billiard path. More progress has been made for outer billiards, though the situation is far from well understood. As mentioned above, all the orbits are periodic when the system is defined relative to a convex rational polygon in the Euclidean plane. Moreover, it is a recent theorem of Chris Culter (written up by Sergei Tabachnikov) that outer billiards relative to any convex polygon has periodic orbits—in fact a periodic orbit outside of any given bounded region. [17]

Open questions

Outer billiards is a subject still in its beginning phase. Most problems are still unsolved. Here are some open problems in the area.

See also

Related Research Articles

<span class="mw-page-title-main">Angle</span> Figure formed by two rays meeting at a common point

In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.

<span class="mw-page-title-main">Dual polyhedron</span> Polyhedron associated with another by swapping vertices for faces

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

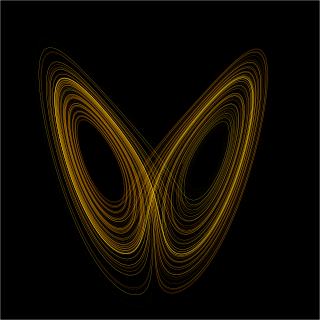
<span class="mw-page-title-main">Dynamical system</span> Mathematical model of the time dependence of a point in space

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

<span class="mw-page-title-main">Convex hull</span> Smallest convex set containing a given set

In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.

<span class="mw-page-title-main">Rectangle</span> Quadrilateral with four right angles

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as  ABCD.

<span class="mw-page-title-main">Kite (geometry)</span> Quadrilateral symmetric across a diagonal

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

<span class="mw-page-title-main">Hyperbolic geometry</span> Non-Euclidean geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

<span class="mw-page-title-main">Tessellation</span> Tiling of a plane in mathematics

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

<span class="mw-page-title-main">Discrete geometry</span> Branch of geometry that studies combinatorial properties and constructive methods

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

<span class="mw-page-title-main">Arrangement of lines</span> Subdivision of the plane by lines

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

Richard Evan Schwartz is an American mathematician notable for his contributions to geometric group theory and to an area of mathematics known as billiards. Geometric group theory is a relatively new area of mathematics beginning around the late 1980s which explores finitely generated groups, and seeks connections between their algebraic properties and the geometric spaces on which these groups act. He has worked on what mathematicians refer to as billiards, which are dynamical systems based on a convex shape in a plane. He has explored geometric iterations involving polygons, and he has been credited for developing the mathematical concept known as the pentagram map. In addition, he is a bestselling author of a mathematics picture book for young children. His published work usually appears under the name Richard Evan Schwartz. In 2018 he is a professor of mathematics at Brown University.

<span class="mw-page-title-main">Convex polytope</span> Convex hull of a finite set of points in a Euclidean space

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the -dimensional Euclidean space . Most texts use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary.

<span class="mw-page-title-main">Principal curvature</span> Maximal and minimal curvature at a point of a surface

In differential geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how the surface bends by different amounts in different directions at that point.

<span class="mw-page-title-main">Surface (mathematics)</span> Mathematical idealization of the surface of a body

In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

<span class="mw-page-title-main">Circle packing theorem</span> Describes the possible tangency relations between circles with disjoint interiors

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In mathematics, the pentagram map is a discrete dynamical system on the moduli space of polygons in the projective plane. The pentagram map takes a given polygon, finds the intersections of the shortest diagonals of the polygon, and constructs a new polygon from these intersections. Richard Schwartz introduced the pentagram map for a general polygon in a 1992 paper though it seems that the special case, in which the map is defined for pentagons only, goes back to an 1871 paper of Alfred Clebsch and a 1945 paper of Theodore Motzkin. The pentagram map is similar in spirit to the constructions underlying Desargues' theorem and Poncelet's porism. It echoes the rationale and construction underlying a conjecture of Branko Grünbaum concerning the diagonals of a polygon.

<span class="mw-page-title-main">Convex curve</span> Type of plane curve

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.

<span class="mw-page-title-main">Binary tiling</span> Tiling of the hyperbolic plane

In geometry, the binary tiling is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. It was first studied mathematically in 1974 by Károly Böröczky. However, a closely related tiling was used earlier in a 1957 print by M. C. Escher.

References

  1. 1 2 3 Tabachnikov, Serge (1995). Billiards. Panoramas et Synthèses. Société Mathématique de France. ISBN   978-2-85629-030-9.
  2. ↑ Tabachnikov, Sergei (2002). "Dual Billiards in the Hyperbolic Plane". Nonlinearity. 15 (4): 1051–1072. Bibcode:2002Nonli..15.1051T. CiteSeerX   10.1.1.408.9436 . doi:10.1088/0951-7715/15/4/305. S2CID   250758250.
  3. ↑ Neumann, Bernhard H. (25 Jan 1959). "Sharing Ham and Eggs". Iota: The Manchester University Mathematics Students' Journal.
  4. 1 2 Moser, Jürgen (1973). Stable and random motions in dynamical systems. Annals of Mathematics Studies. Vol. 77. Princeton University Press.
  5. ↑ Moser, Jürgen (1978). "Is the Solar System Stable?". Mathematical Intelligencer. 1 (2): 65–71. doi:10.1007/BF03023062.
  6. ↑ R. Douady (1982). "these de 3-eme cycle". University of Paris 7.{{cite journal}}: Cite journal requires |journal= (help)
  7. ↑ Vivaldi, Franco; Shaidenko, Anna V. (1987). "Global Stability of a class of discontinuous billiards". Communications in Mathematical Physics . 110 (4): 625–640. Bibcode:1987CMaPh.110..625V. doi:10.1007/BF01205552. S2CID   111386812.
  8. ↑ Kołodziej, Rafał (1989). "The antibilliard outside a polygon". Bull. Polish Acad. Sci. Math. 34: 163–168.
  9. ↑ Gutkin, Eugene; Simanyi, Nandor (1991). "Dual polygonal billiard and necklace dynamics". Communications in Mathematical Physics . 143 (3): 431–450. Bibcode:1992CMaPh.143..431G. doi:10.1007/BF02099259. S2CID   121776396.
  10. ↑ Boyland, Philip (1996). "Dual billiards, twist maps, and impact oscillators". Nonlinearity . 9 (6): 1411–1438. arXiv: math/9408216 . Bibcode:1996Nonli...9.1411B. doi:10.1088/0951-7715/9/6/002. S2CID   18709638.
  11. ↑ Genin, Daniel I. (2005). Regular and chaotic dynamics of outer billiards (Ph.D. Thesis). Pennsylvania State University.
  12. ↑ Schwartz, Richard E. (2007). "unbounded orbits for outer billiards I". Journal of Modern Dynamics . 1 (3): 371–424. arXiv: math/0702073 . Bibcode:2007math......2073S. doi:10.3934/jmd.2007.1.371. S2CID   119146537.
  13. ↑ Schwartz, Richard E. (2009). "outer billiards on kites". Annals of Mathematics Studies. 171. Princeton University Press.{{cite journal}}: Cite journal requires |journal= (help)
  14. ↑ Dolgopyat, Dmitry; Fayad, Bassam (2009). "unbounded orbits for semicircular outer billiards". Annales Henri Poincaré . 10 (2): 357–375. Bibcode:2009AnHP...10..357D. doi: 10.1007/s00023-009-0409-9 .
  15. ↑ Doǧru, Filiz; Tabachnikov, Sergei (2003). "On Polygonal Dual Billiards in the Hyperbolic Plane". Regular and Chaotic Dynamics. 8 (1): 67–82. Bibcode:2003RCD.....8...67D. doi:10.1070/RD2003v008n01ABEH000226.
  16. ↑ Doǧru, Filiz; Otten, Samuel (2011). "Sizing Up Outer Billiard Tables". American Journal of Undergraduate Research. 10: 1–8. doi: 10.33697/ajur.2011.008 .
  17. ↑ Tabachnikov, Serge (2007). "A proof of Culter's theorem on existence of periodic orbits in polygonal outer billiards". Geometriae Dedicata . 129: 83–87. arXiv: 0706.1003 . Bibcode:2007arXiv0706.1003T. doi: 10.1007/s10711-007-9196-y .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.