Eclipse cycle

Eclipses may occur repeatedly, separated by certain intervals of time: these intervals are called eclipse cycles. ^[1] The series of eclipses separated by a repeat of one of these intervals is called an eclipse series.

Contents

• Eclipse conditions
• Recurrences
• Periodicity
• Repetition of solar eclipses
• Repetition of lunar eclipses
• Eclipses would not occur in every month
• Numerical values
• Eclipse cycles
• Notes
• Saros series and inex series
• Properties of eclipses
• Long-term trends
• See also
• References
• External links

Eclipse conditions

Eclipses may occur when Earth and the Moon are aligned with the Sun, and the shadow of one body projected by the Sun falls on the other. So at new moon, when the Moon is in conjunction with the Sun, the Moon may pass in front of the Sun as viewed from a narrow region on the surface of Earth and cause a solar eclipse. At full moon, when the Moon is in opposition to the Sun, the Moon may pass through the shadow of Earth, and a lunar eclipse is visible from the night half of Earth. The conjunction and opposition of the Moon together have a special name: syzygy (Greek for "junction"), because of the importance of these lunar phases.

An eclipse does not occur at every new or full moon, because the plane of the Moon's orbit around Earth is tilted with respect to the plane of Earth's orbit around the Sun (the ecliptic): so as viewed from Earth, when the Moon appears nearest the Sun (at new moon) or furthest from it (at full moon), the three bodies are usually not exactly on the same line.

This inclination is on average about 5° 9′, much larger than the apparent mean diameter of the Sun (32′ 2″), the Moon as viewed from Earth's surface directly below the Moon (31′ 37″), and Earth's shadow at the mean lunar distance (1° 23′).

Therefore, at most new moons, Earth passes too far north or south of the lunar shadow, and at most full moons, the Moon misses Earth's shadow. Also, at most solar eclipses, the apparent angular diameter of the Moon is insufficient to fully occlude the solar disc, unless the Moon is around its perigee, i.e. nearer Earth and apparently larger than average. In any case, the alignment must be almost perfect to cause an eclipse.

An eclipse can occur only when the Moon is on or near the plane of Earth's orbit, i.e. when its ecliptic latitude is low. This happens when the Moon is around either of the two orbital nodes on the ecliptic at the time of the syzygy. Of course, to produce an eclipse, the Sun must also be around a node at that time – the same node for a solar eclipse or the opposite node for a lunar eclipse.

Recurrences

Up to three eclipses may occur during an eclipse season, a one- or two-month period that happens twice a year, around the time when the Sun is near the nodes of the Moon's orbit.

An eclipse does not occur every month, because one month after an eclipse the relative geometry of the Sun, Moon, and Earth has changed.

As seen from the Earth, the time it takes for the Moon to return to a node, the draconic month, is less than the time it takes for the Moon to return to the same ecliptic longitude as the Sun: the synodic month. The main reason is that during the time that the Moon has completed an orbit around the Earth, the Earth (and Moon) have completed about 1⁄13 of their orbit around the Sun: the Moon has to make up for this in order to come again into conjunction or opposition with the Sun. Secondly, the orbital nodes of the Moon precess westward in ecliptic longitude, completing a full circle in about 18.60 years, so a draconic month is shorter than a sidereal month. In all, the difference in period between synodic and draconic month is nearly 2+1⁄3 days. Likewise, as seen from the Earth, the Sun passes both nodes as it moves along its ecliptic path. The period for the Sun to return to a node is called the eclipse or draconic year: about 346.6201 days, which is about 1⁄20 year shorter than a sidereal year because of the precession of the nodes.

If a solar eclipse occurs at one new moon, which must be close to a node, then at the next full moon the Moon is already more than a day past its opposite node, and may or may not miss the Earth's shadow. By the next new moon it is even further ahead of the node, so it is less likely that there will be a solar eclipse somewhere on Earth. By the next month, there will certainly be no event.

However, about 5 or 6 lunations later the new moon will fall close to the opposite node. In that time (half an eclipse year) the Sun will have moved to the opposite node too, so the circumstances will again be suitable for one or more eclipses.

Periodicity

The periodicity of solar eclipses is the interval between any two solar eclipses in succession, which will be either 1, 5, or 6 synodic months. ^[2] It is calculated that the Earth will experience a total number of 11,898 solar eclipses between 2000 BCE and 3000 CE. A particular solar eclipse will be repeated approximately after every 18 years 11 days and 8 hours (6,585.32 days) of period, but not in the same geographical region. ^[3] A particular geographical region will experience a particular solar eclipse in every 54 years 34 days period. ^[2] Total solar eclipses are rare events, although they occur somewhere on Earth every 18 months on average. ^[4]

Numerical values

These are the lengths of the various types of months as discussed above (according to the lunar ephemeris ELP2000-85, valid for the epoch J2000.0; taken from (e.g.) Meeus (1991) ):

SM = 29.530588853 days (Synodic month) ^[8]

DM = 27.212220817 days (Draconic month) ^[9]

AM = 27.55454988 days (Anomalistic month) ^[10]

EY = 346.620076 days (Eclipse year)

Note that there are three main moving points: the Sun, the Moon, and the (ascending) node; and that there are three main periods, when each of the three possible pairs of moving points meet one another: the synodic month when the Moon returns to the Sun, the draconic month when the Moon returns to the node, and the eclipse year when the Sun returns to the node. These three 2-way relations are not independent (i.e. both the synodic month and eclipse year are dependent on the apparent motion of the Sun, both the draconic month and eclipse year are dependent on the motion of the nodes), and indeed the eclipse year can be described as the beat period of the synodic and draconic months (i.e. the period of the difference between the synodic and draconic months); in formula:

${\displaystyle {\mbox{EY}}={\frac {{\mbox{SM}}\times {\mbox{DM}}}{{\mbox{SM}}-{\mbox{DM}}}}}$

as can be checked by filling in the numerical values listed above.

Eclipse cycles have a period in which a certain number of synodic months closely equals an integer or half-integer number of draconic months: one such period after an eclipse, a syzygy (new moon or full moon) takes place again near a node of the Moon's orbit on the ecliptic, and an eclipse can occur again. However, the synodic and draconic months are incommensurate: their ratio is not an integer number. We need to approximate this ratio by common fractions: the numerators and denominators then give the multiples of the two periods – draconic and synodic months – that (approximately) span the same amount of time, representing an eclipse cycle.

These fractions can be found by the method of continued fractions: this arithmetical technique provides a series of progressively better approximations of any real numeric value by proper fractions.

Since there may be an eclipse every half draconic month, we need to find approximations for the number of half draconic months per synodic month: so the target ratio to approximate is: SM / (DM/2) = 29.530588853 / (27.212220817/2) = 2.170391682

The continued fractions expansion for this ratio is:

2.170391682 = [2;5,1,6,1,1,1,1,1,11,1,...]: [11]  Quotients  Convergents            half DM/SM     decimal      named cycle (if any)     2;           2/1    = 2            synodic month     5           11/5    = 2.2          pentalunex     1           13/6    = 2.166666667  semester     6           89/41   = 2.170731707  hepton     1          102/47   = 2.170212766  octon     1          191/88   = 2.170454545  tzolkinex     1          293/135  = 2.170370370  tritos     1          484/223  = 2.170403587  saros     1          777/358  = 2.170391061  inex    11         9031/4161 = 2.170391732  selebit     1         9808/4519 = 2.170391679  square year   ...

The ratio of synodic months per half eclipse year yields the same series:

5.868831091 = [5;1,6,1,1,1,1,1,11,1,...] Quotients  Convergents            SM/half EY  decimal        SM/full EY  named cycle     5;      5/1      = 5                          pentalunex     1       6/1      = 6              12/1        semester     6      41/7      = 5.857142857                hepton     1      47/8      = 5.875          47/4        octon     1      88/15     = 5.866666667                tzolkinex     1     135/23     = 5.869565217                tritos     1     223/38     = 5.868421053   223/19       saros     1     358/61     = 5.868852459   716/61       inex    11    4161/709    = 5.868829337                selebit     1    4519/770    = 5.868831169  4519/385      square year   ...

Each of these is an eclipse cycle. Less accurate cycles may be constructed by combinations of these.

Eclipse cycles

This table summarizes the characteristics of various eclipse cycles, and can be computed from the numerical results of the preceding paragraphs; cf. Meeus (1997) Ch.9. More details are given in the comments below, and several notable cycles have their own pages. Many other cycles have been noted, some of which have been named. ^[3]

The number of days given is the average. The actual number of days and fractions of days between two eclipses varies because of the variation in the speed of the Moon and of the Sun in the sky. The variation is less if the number of anomalistic months is near a whole number, and if the number of anomalistic years is near a whole number. (See graphs lower down of semester and Hipparchic cycle.)

Any eclipse cycle, and indeed the interval between any two eclipses, can be expressed as a combination of saros (s) and inex (i) intervals. These are listed in the column "formula".

Notes

Fortnight

Half a synodic month (29.53 days). When there is an eclipse, there is a fair chance that at the next syzygy there will be another eclipse: the Sun and Moon will have moved about 15° with respect to the nodes (the Moon being opposite to where it was the previous time), but the luminaries may still be within bounds to make an eclipse. For example, penumbral lunar eclipse of May 26, 2002 is followed by the annular solar eclipse of June 10, 2002 and penumbral lunar eclipse of June 24, 2002. The shortest lunar fortnight between a new moon and a full moon lasts only about 13 days and 21.5 hours, while the longest such lunar fortnight lasts about 15 days and 14.5 hours. (Due to evection, these values are different going from quarter moon to quarter moon. The shortest lunar fortnight between first and last quarter moons lasts only about 13 days and 12 hours, while the longest lasts about 16 days and 2 hours.)

For more information see eclipse season.

Synodic month

Similarly, two events one synodic month apart have the Sun and Moon at two positions on either side of the node, 29° apart: both may cause a partial solar eclipse. For a lunar eclipse, it is a penumbral lunar eclipse.

Pentalunex

5 synodic months. Successive solar or lunar eclipses may occur 1, 5 or 6 synodic months apart. ^[3] When two solar eclipses are one month apart, one will be seen near the Arctic Circle and the other near the Antarctic Circle. When they are five months apart, they are both seen near the Arctic Circle or both near the Antarctic Circle.

Semester

Half a lunar year. Eclipses will repeat exactly one semester apart at alternating nodes in a cycle that lasts for 8 or 9 eclipses. Because it is close to a half integer of anomalistic, draconic months, and tropical years, each solar eclipse will (usually) alternate between hemispheres each semester, as well as alternate between total and annular. Hence there is usually a maximum of one total or annular eclipse each in a given lunar year. (However, in the middle of an eight-semester series the hemispheres switch, and there is a switch during the series between whether the odd ones or the even ones are total.) It is possible to have two eclipses separated by a semester and a third eclipse one month before or after, so that two of the three are separated by seven months, but this only happens during certain centuries (see graph of inex versus date below). Because it is close to a half integer of anomalistic, draconic months, and tropical years, each lunar eclipse will usually alternate between edges of Earth's shadow each semester, as well as alternate between Lunar eclipses with the moon’s penumbral and umbral shadow difference less or greater than 1. Hence there is usually a maximum of one Lunar eclipse with Moon’s penumbral and umbral shadow difference less or greater than 1 each in a given lunar year.

Lunar year

Twelve (synodic) months, a little longer than an eclipse year: the Sun has returned to the node, so eclipses may again occur:

Hexon

6 eclipse seasons, and a fairly short eclipse cycle. Each eclipse in a hexon series (except the last) is followed by an eclipse whose saros series number is 8 lower, always occurring at the same node. It is equal to 35 synodic months, 1 less than 3 lunar years (36 synodic months). At any given time there are six hexon series active.

Hepton

7 eclipse seasons, and one of the less noteworthy eclipse cycles. Each eclipse in a hepton is followed by an eclipse 3 saros series before, always occurring at alternating nodes. It is equal to 41 synodic months. The interval is nearly a whole number of weeks (172.96), so each eclipse is followed by another that is usually on the same day of the week (moving backwards irregularly by an average of a quarter day). At any given time there are seven hepton series active.

Octon

8 eclipse seasons, 1⁄5 of the Metonic cycle, and a fairly decent short eclipse cycle, but poor in anomalistic returns. Each octon in a series is 2 saros apart, always occurring at the same node. It is equal to 47 synodic months. At any given time there are eight octon series active.

Tzolkinex

Includes a half draconic month, so occurs at alternating nodes and alternates between hemispheres. Each consecutive eclipse is a member of preceding saros series from the one before. Equal to nearly ten tzolk'ins. Every third tzolkinex in a series is near an integer number of anomalistic months and so will have similar properties.

Hibbardina

An eclipse "cycle" of at most 3 eclipses, but in fact meant as a period separating a pair of similar eclipses with opposite gamma values. Adding 1 lunation (for 112 synodic months) gives another period with the same property, the other half of a saros. The two surround a sar (half-saros). Named for William B. Hibbard who identified it in 1956. ^[3] One lunar year less than a Hibbardina, 99 lunations, is only about a day and a half more than eight years.

Sar (half saros)

Includes an odd number of fortnights (223). As a result, eclipses alternate between lunar and solar with each cycle, occurring at the same node and with similar characteristics. A solar eclipse with small gamma will be followed by a very central total lunar eclipse. A solar eclipse where the Moon's penumbra just barely grazes the southern limb of Earth will be followed half a saros later by a lunar eclipse where the Moon just grazes the southern limb of the Earth's penumbra. ^[3]

Tritos

Equal to an inex minus a saros. A triple tritos is close to an integer number of anomalistic months and so will have similar properties.

Saros

The best known eclipse cycle (described in the Almagest but not given this name), and one of the best for predicting eclipses, in which 223 synodic months equal 242 draconic months with an error of only 51 minutes. It is also very close to 239 anomalistic months, which makes the circumstances between two eclipses one saros apart very similar. Being a third of a day more than a whole number of days, each succeeding eclipse is centered about 120° further west over the Earth. If the Earth's orbit around the sun were circular, the saros cycle would be very close to a periodic orbit that would repeat exactly every 223 months.ὤ ^[12]

Metonic cycle or enneadecaeteris

Nearly 6940 days, but as an eclipse cycle can be taken as 235 synodic months. This is just an hour and a half less than 19 years of 365+1⁄4 days. It is also 5 "octon" periods and close to 20 eclipse years, so it yields a short series of four or five eclipses on the same calendar date or on two calendar dates. It is equivalent to 110 "hollow months" of 29 days and 125 "full months" of 30 days.

Semanex

Equal to a whole number of weeks plus a hundredth of a day, so consecutive eclipses of the cycle are usually on the same day of the week. Each eclipse in this period is a member of a preceding saros series, always occurring on alternating nodes. ^[3]

Thix

This eclipse cycle is just over 36 tzolk'ins, lasting 317 lunations. Each eclipse in this period is followed by an eclipse 4 saros series' later, always occurring on the same node. ^[3]

Inex

Very convenient in the classification of eclipse cycles. One inex after an eclipse, another eclipse takes place at the opposite latitude. Inex series, after a sputtering beginning, go on for many thousands of years giving eclipses every 29 years minus 20 days, or 21 days if the last year has 366 days. Eighteen inex cycles (see "Basic period") are equal to 520.9996 Julian years so an inex is ⁠28+17/18⁠ Julian years. The inex cycle is the cycle that produces the highest number of eclipses while it lasts. Inex series 30 first produced a solar eclipse in saros series -245 (in 9435 BC), has been producing eclipses every 29 years since saros series -197 (in 8045 BC), and will continue long past AD 15,000, ^[13] by which time it will have produced 707 consecutive eclipses. The name was introduced by George van den Bergh in 1951. ^[3]

Exeligmos

A triple saros, with the advantage that it has nearly an integer number of days, so the next eclipse will be visible at locations near the eclipse that occurred one exeligmos earlier, in contrast to the saros, in which the eclipse occurs about 8 hours later in the day or about 120° to the west of the eclipse that occurred one saros earlier. Ptolemy in the Almagest mentions it after discussing what we now call the saros, and says that it is called the exeligmos (ἐξελιγμός, meaning "unrolling").

Aubrey cycle

Named for the calculation of eclipses measured with Aubrey holes, located at Stonehenge. With 1385 fortnights, eclipses alternate between lunar and solar in 56 years minus 3.5 days. ^[3]

Unidos

Very close to 65 years. Equals 67 lunar years and exceeds 65 Julian years by only 1.3 days (1.8 days over 65 average Gregorian years). Name suggested by Karl Palmen in that 2 saros are added over an inex. ^[3] A period of three Unidos (195 years, a "Trihex") is quite close to both a whole number of anomalistic years and a whole number of anomalistic months, which means the interval between two eclipses is quite constant.

Callippic cycle

Originally defined as 4 Metonic cycles minus one day or precisely 76 years of 365+1⁄4 days. In the table, taken as 940 synodic months, equivalent to 441 hollow months and 499 full months. This cycle, though useful for example in the calculation of the date of Easter, can produce at most two solar eclipses (both partial) and at most two lunar eclipses (both penumbral). The Callipic cycle is 20 octons, and series of octons often produce only 21 eclipses, so only the first and the last of such a series are separated by a Callipic cycle. Most eclipses are not followed by another eclipse 940 lunations later, but rather 939 lunations later (two inex and a saros), which comes near an integer number of draconic months, producing similar eclipses. This is called a Short Callippic Period. ^[3]

Triad

A triple inex, with the advantage that it has nearly an integer number of anomalistic months, which makes the circumstances between two eclipses one Triad apart very similar, but at the opposite latitude. Almost exactly 87 calendar years minus 2 months. The triad means that every third saros series will be similar (central eclipses mostly total or mostly annular for example). Solar saros 130, 133, 136, 139, 142 and 145, for example, all produce mainly total eclipses when they are central, because the moon is close to perigee. In fact, at the solar eclipse of October 17, 1781, which was in saros series 130 and inex 50, was both very central and at perigee. ^[12] But this repetition is not perfect. In about 2460 years, the above-mentioned series, 130, 133... (equivalent to 1 modulo 3) will give central solar eclipses that are annular, near apogee. In about 820 years central lunar eclipses, but not solar ones, will be near perigee every three saros series, and in around 1640 years the solar saros series with index equivalent to 2 modulo 3 will give central eclipses near perigee. ^[14]

Quarter Palmen cycle

Named after Karl Palmen in that a saros is subtracted from 4 inex. Each eclipse is followed by an eclipse 4 saros series later, always occurring at the same node. It equals 97 years 9 months or 1209 lunations. ^[3]

Mercury cycle

Equals approximately 353 synodic periods of Mercury, ^[15] so that eclipses synchronize with the timing of Mercury's position in its orbit during each period, equaling 112 years minus one week or 1385 lunations. ^[3]

Tritrix

Equals 3 inex plus 3 saros, which is 140 years 11 months or 1743 lunations, always occurring on alternating nodes. ^[3] The tritrix is very close to a whole number of anomalistic months ((1867.9970) and close to a whole number of anomalistic years, which means the interval between two eclipses is quite constant. Two tritrix minus a saros (3263 lunations) is even closer to a whole number of anomaalistic months (3497.0018), being exactly thirteen seventeenths of the Cycle of Hipparchus (see below).

de la Hire cycle

A sextuple inex, adopted by Phillippe de la Hire in his Tabularum Astronomicarum in 1687. It equals 6 inex periods, which is 173 years and around 8 months, or 2148 lunations, equaling 179 lunar years, always occurring on the same node at nearly an integer number of anomalistic months, as it equals 2 triads. ^[3]

Trihex

Equals 3 inex plus 6 saros, lasting 195 Julian years and 4 days or 2412 lunations, equaling 201 lunar years, always occurring at alternating nodes. Just two days over a whole number of anomalistic years and near a whole number of anomalistic months, which means the interval between two eclipses is quite constant.

Lambert II cycle

An eclipse cycle in which eclipses occur in similar circumstances, according to Johann Heinrich Lambert in 1765. (The "Lambert I cycle is what we also call the inex.) Very close to a half-integer number of draconic months. It equals about 278 and a half years. ^[3]

Macdonald cycle

An eclipse cycle equal to 299 years and about ten and a half months, always occurring on the same node. Peter Macdonald found that a series of eclipses of especially long duration visible from Britain occurs with this interval in the period AD 1 to 3000. ^[3] A Macdonald series has around ten eclipses and lasts about 3000 years. All or most are on the same day of the week, since the interval is only about an hour less than a whole number of weeks and the length is fairly constant becauses the anomaly of the moon is almost constant.

Utting cycle

The seventh convergent in the continued fractions development between the ratio of the eclipse year and synodic month, if this ratio is approximated as between 2.17039173 and 2.17039179. Discussed by James Utting in 1827. ^[3]

Selebit

An eclipse cycle where the number of eclipse years (354.5) closely matches (by chance) the number of days in a lunar year (354.371). It equals approximately 336 years 5 months 6 days or 4161 lunations. It is a convergent in the continued fractions development of the ratio between the eclipse year and the synodic month, giving a series of eclipses one selebit apart a life expectancy of thousands of years.

Cycle of Hipparchus

Not a long-lasting eclipse cycle, but Hipparchus constructed it to closely match an integer number of synodic and anomalistic months, years (345), and days. Because of it being close to a whole number of both anomalistic months and anomalistic years, its length is always within about an hour of 126007 days and half an hour. (See graphs lower down of semester and Hipparchic cycle.) This means that at the time of the second eclipse same side of the earth will be facing the sun as at the first eclipse (but the value of gamma will be different). By comparing his own eclipse observations with Babylonian records from 345 years earlier, Hipparchus could verify the accuracy of the various periods that the Chaldeans used. Ptolemy points out that dividing it by 17 still gives a whole number of synodic months (251) and anomalistic months (269), but this is not an eclipse interval because it is not near a whole or half integer number of draconic months.

Square year

An eclipse cycle where the number of solar years (365.371) closely matches (by chance) the number of days in 1 solar year (365.242). Lasting 365 years 4.5 months or 4519 lunations. It is the eighth convergent in the continued fractions development of the ratio between the eclipse year and the synodic month, giving a series of eclipses one square year apart a life expectancy of thousands of years. Many eclipses of our day belong to "square year" series or selebit series that have been going for over 13,000 years, and many will continue for over 13,000 years. ^{[13] [3]}

Gregoriana

Known for returning toward the same day of the week and Gregorian calendar date, as approximately an integer number of years, months, and weeks, are achieved, usually moving only a quarter day later in the Gregorian calendar. ^{[3] [16]}

Hexdodeka

Equal to six Unidos or two Trihex. Useful for giving accurate calculations of the timing of lunisolar syzygies. ^[3]

Grattan Guinness cycle

The shortest cycle that gives eclipses on the same date (more or less) in both the Gregorian and in a 12-month lunar calendar, because it is almost exactly a whole number of Gregorian years (391.00029) as well as being exactly 403 12-month lunar years. Discovered by Henry Grattan Guinness in a speculative interpretation of Revelation 9:15. ^{[17] [3]}

Hipparchian

Fourteen inex plus two saros. The Almagest attributes this cycle to Hipparchus. George van den Bergh called it the "Long Babylonian Period" or the "Old Babylonian Period", but there is no evidence that the Babylonians were aware of it. ^[3]

Basic period

Achieves nearly an integer number (521) of Julian years, anomalistic years (521 anomalistic years minus 5 days), and weeks (27185 weeks plus 0.1 day), leading to eclipses on the same day of the Julian calendar and week. ^[3]

Chalepe

Equals 18 inex plus 2 saros, therefore 557 years plus about 1 month. ^[3]

Tetradia

Sometimes 4 total lunar eclipses occur in a row with intervals of 6 lunations (one semester) between them, and this is called a tetrad. Giovanni Schiaparelli noticed that there are eras when such tetrads occur comparatively frequently, interrupted by eras when they are rare. This variation takes about 6 centuries. Antonie Pannekoek (1951) offered an explanation for this phenomenon and found a period of 591 years. Van den Bergh (1954) from Theodor von Oppolzer's Canon der Finsternisse found a period of 586 years. This happens to be an eclipse cycle; see Meeus [I] (1997). The phenomenon is related to the elliptical orbit of the Earth, as explained below. Recently Tudor Hughes explained that secular changes in the eccentricity of the Earth's orbit cause the period for occurrence of tetrads to be variable, and it is currently about 565 years; see Meeus III (2004) for a detailed discussion. The Tetradia period also shows up in the distance between eras in which there are pairs of (non-consecutive) eclipses seven months apart, or eras in which there are more pairs of eclipses one month apart, or eras in which there are saros series in which gamma is fairly constant for many decades, or eras with more low-gamma eclipses. ^[14]

Hyper exeligmos

Equals 12 "Short Callippic Periods" (each a month shorter than a Callipic cycle), or 12 Callippic cycles minus 1 lunar year, so therefore a bit over 911 years or 11268 lunations, which is 939 lunar years. First mentioned by Alexander Pogo in 1935. ^[3]

The next nine cycles, Cartouche through Accuratissima, are all similar, being equal to 52 inex periods plus up to two triads and various numbers of saros periods. This means they all have a near-whole number of anomalistic months. They range from 1505 to 1841 years, and each series lasts for many thousands of years.

Cartouche

Equals 52 inex, therefore 1505 years and between 1 and 2 months. Eclipses in this period occur at a similar distance as nearly an integer number of anomalistic months are achieved. ^[3]

Palaea-Horologia

Equals 55 inex plus 3 saros, which is over 1646 years. Useful for calculating the timing of eclipses. Close to a whole number of anomalistic months. A series lasts tens of thousands of years. ^[3]

hybridia

Equals 55 inex plus 4 saros, one saros more than a Palaea-Horologia, therefore over 1664 years, near an integer number of anomalistic months, therefore having similar properties, but at the opposite latitude. ^[3]

Selenid

One saros more than a Hybridia. The name for eclipse cycles useful for calculating the magnitudes of eclipses in the 3rd millennium. George van den Bergh first mentioned a period of 55 inex plus 5 saros (over 1682 years) before mentioning a period of 95 inex plus 11 saros (over 2948 years) in 1951. ^[3]

Proxima

Equals 58 inex plus 5 saros, therefore a bit less than 1769 years, always occurring at the same node and toward an integer number of draconic and anomalistic months and weeks, making the circumstances of each eclipse a proxima apart similar in character. ^[3]

Heliotrope

Equals 58 inex plus 6 saros, one saros more than a Proxima, therefore about 1787 years. Useful for calculating the longitudinal positions of the central lines of eclipses on Earth's surface near an integer number of years (1786.954 Julian years, 1786.991 Gregorian). ^[3]

Megalosaros

Equals 58 inex plus 7 saros (one saros more than a Heliotrope), which is 95 Metonic cycles, or 95 saros plus 95 lunar years, or 100 saros plus 25 lunations, or a bit over 1805 years, always occurring on the same node, and revealing the Metonic cycle's mismatch from 19 years as 95 repeats accumulates the mismatch to about three years. The extra 25 lunations are needed because 100 saros cycles exceeds the life expectancy of a saros series. ^{[3] [18]}

Immobilis

Equals 58 inex plus 8 saros (one saros more than a Megalosaros), which is exactly 1879 lunar years. Always occurs on the same node. Very close to a whole number of anomalistic months, although 43 inex minus 5 saros (14279 months, 1154.5 years) is even closer. ^[3]

Accuratissima

Equals 58 inex plus 9 saros (one saros more than an Immobilis), therefore 1841 years 1 month or 22771 lunations, which is presently about an hour more than a whole number of weeks, allowing eclipses to occur the same day of the week. Because of the slowing of the Earth's rotation, the length of the Accuratissima will become exactly equal to a whole number of days or weeks in around AD 2100, meaning that an eclipse around AD 1200 will be repeated at the same time of day on the same day of the week 1841 years later. The Accuratissima is also useful for calculating the magnitude and character of eclipses. ^[3] An Accuratissima plus a Tritrix plus a saros makes an eclipse cycle 1.8 days short of 2000 Julian years, or 13.2 days longer than 2000 Gregorain years. It is only half a day less than a whole number of anomalistic months, whereas the Accuratisssima is only 0.2 days short of a whole number of anomalistic months.

Mackay cycle

Equals 76 inex plus 9 saros, therefore 2362 years and about a month, always occurring on the same node. Mentioned by A. Mackay in the 1800's. ^[3]

Horologia

Equals 110 inex plus 7 saros, therefore 3310 years and about 2 months, always occurring on the same node. It is useful for calculating the timing and magnitudes of eclipses as they are approximately an integer number of draconic and anomalistic months and weeks apart (172,715.97 weeks), leading to similar eclipses in character and week timing. ^[3]

Saros series and inex series

Any eclipse can be assigned to a given saros series and inex series. The year of a solar eclipse (in the Gregorian calendar) is then given approximately by: ^[19]

year = 28.945 × number of the saros series + 18.030 × number of the inex series − 2882.55

When this is greater than 1, the integer part gives the year AD, but when it is negative the year BC is obtained by taking the integer part and adding 2. For instance, the eclipse in saros series 0 and inex series 0 was in the middle of 2884 BC.

A "panorama" of solar eclipses arranged by saros and inex has been produced by Luca Quaglia and John Tilley showing 61775 solar eclipses from 11001 BC to AD 15000 (see below). ^[20] Each column of the graph is a complete Saros series which progresses smoothly from partial eclipses into total or annular eclipses and back into partials. Each graph row represents an inex series. Since a saros, of 223 synodic months, is slightly less than a whole number of draconic months, the early eclipses in a saros series (in the upper part of the diagram) occur after the Moon goes through its node (the beginning and end of a draconic month), while the later eclipses (in the lower part) occur before the Moon goes through its node. Every 18 years, the eclipse occurs on average about half a degree further west with respect to the node, but the progression is not uniform.

Saros and inex number can be calculated for an eclipse near a given date. One can also find the approximate date of solar eclipses at distant dates by first determining one in an inex series such as series 50. This can be done by adding or subtracting some multiple of 28.9450 Gregorian years from the solar eclipse of 10 May, 2013, or 28.9444 Julian years from the Julian date of 27 April, 2013. Once such an eclipse has been found, others around the same time can be found using the short cycles. For lunar eclipses, the anchor dates May 4, 2004 or Julian April 21 may be used.

Saros and inex numbers are also defined for lunar eclipses. A solar eclipse of given saros and inex series will be preceded a fortnight earlier by a lunar eclipse whose saros number is 26 lower and whose inex number is 18 higher, or it will be followed a fortnight later by a lunar eclipse whose saros number is 12 higher and whose inex number is 43 lower. As with solar eclipses, the Gregorian year of a lunar eclipse can be calculated as:

year = 28.945 × number of the saros series + 18.030 × number of the inex series − 2454.564

Lunar eclipses can also be plotted in a similar diagram, this diagram covering 1000 AD to 2500 AD. The yellow diagonal band represents all the eclipses from 1900 to 2100. This graph immediately illuminates that this 1900–2100 period contains an above average number of total lunar eclipses compared to other adjacent centuries.

This is related to the fact that tetrads (see above) are more common at present than at other periods. Tetrads occur when four lunar eclipses occur at four lunar inex numbers, decreseing by 8 (that is, a semester apart), which are in the range giving fairly central eclipses (small gamma), and furthermore the eclipses take place around halfway between the Earth's perihelion and aphelion. For example, in the tetrad of 2014-2015 (the so-called Four Blood Moons), the inex numbers were 52, 44, 36, and 28, and the eclipses occurred in April and late September-early October. Normally the absolute value of gamma decreases and then increases, but because in April the Sun is further east than its mean longitude, and in September/October further west than its mean longitude, the absolute values of gamma in the first and fourth eclipse are decreased, while the absolute values in the second and third are increased. The result is that all four gamma values are small enough to lead to total lunar eclipses. The phenomenon of the Moon "catching up" with the Sun (or the point opposite the Sun), which is usually not at its mean longitude, has been called a "stern chase". ^[21]

Inex series move slowly through the year, each eclipse occurring about 20 days earlier in the year, 29 years later. This means that over a period of 18.2 inex cycles (526 years) the date moves around the whole year. But because the perihelion of Earth's orbit is slowly moving as well, the inex series that are now producing tetrads will again be halfway between Earth's perihelion and aphelion in about 586 years. ^[14]

One can skew the graph of inex versus saros for solar or lunar eclipses so that the x axis shows the time of year. (An eclipse which is two saros series and one inex series later than another will be only 1.8 days later in the year in the Gregorian calendar.) This shows the 586-year oscillations as oscillations that go up around perihelion and down around aphelion (see graph).

Properties of eclipses

The properties of eclipses, such as the timing, the distance or size of the Moon and Sun, or the distance the Moon passes north or south of the line between the Sun and the Earth, depend on the details of the orbits of the Moon and the Earth. There exist formulae for calculating the longitude, latitude, and distance of the Moon and of the Sun using sine and cosine series. The arguments of the sine and cosine functions depend on only four values, the Delaunay arguments:

• D, the mean elongation (angle between the Sun and Moon longitudes)
• F, the mean argument of latitude (the angle between the Moon and the ascending node)
• l, the mean anomaly of the Moon (how far the Moon is from perigee)
• l', the mean anomaly of the Sun (or of the Earth)

These four arguments are basically linear functions of time but with slowly varying higher-order terms. A diagram of inex and saros indices such as the "Panorama" shown above is like a map, and we can consider the values of the Delaunay arguments on it. The mean elongation, D, goes through 360° 223 times when the inex value goes up by 1, and 358 times when the saros value goes up by 1. It is thus equivalent to 0°, by definition, at each combination of solar saros index and inex index, because solar eclipses occur when the elongation is zero. From D one can find the actual elapsed time from some reference time such as J2000, which is like a linear function of inex and saros but with a deviation that grows quadratically with distance from the reference time, amounting to about 19 minutes at a distance of 1000 years. The mean argument of latitude, F, is equivalent to 0° or 180° (depending on whether the saros index is even or odd) along the smooth curve going through the centre of the band of eclipses, where gamma is near zero (around inex series 50 at present). F decreases as we go away from this curve towards higher inex series, and increases on the other side, by about 0.5° per inex series. When the inex value is too far from the centre, the eclipses disappear because the Moon is too far north or south of the Sun. The mean anomaly of the Sun is a smooth function, increasing by about 10° when increasing inex by 1 in a saros series and decreasing by about 20° when increasing saros index by 1 in an inex series. This means it is almost constant when increasing inex by 1 and saros index by 2 (the "Unidos" interval of 65 years). The above graph showing the time of year of eclipses basically shows the solar anomaly, since the perihelion moves by only one day per century in the Julian calendar, or 1.7 days per century in the Gregorian calendar. The mean anomaly of the Moon is more complicated. If we look at the eclipses whose saros index is divisible by 3, then the mean anomaly is a smooth function of inex and saros values. Contours run at an angle, so that mean anomaly is fairly constant when inex and saros values increase together at a ratio of around 21:24. The function varies slowly, changing by only 7.4° when changing the saros index by 3 at a constant inex value. A similar smooth function obtains for eclipses with saros modulo 3 equal to 1, but shifted by about 120°, and for saros modulo 3 equal to 2, shifted by 120° the other way. ^{[22] [23]}

The upshot is that the properties vary slowly over the diagram in any of the three sets of saros series. The accompanying graph shows just the saros series that have saros index modulo 3 equal to zero. The blue areas are where the mean anomaly of the Moon is near 0°, meaning that the Moon is near perigee at the time of the eclipse, and therefore relatively large, favoring total eclipses. In the red area, the Moon is generally further from the Earth, and the eclipses are annular. We can also see the effect of the Sun's anomaly. Eclipses in July, when the Sun is further from the Earth, are more likely to be total, so the blue area extends over a greater range of inex index than for eclipses in January.

The waviness seen in the graph is also due to the Sun's anomaly. In April the Sun is further east than if its longitude progressed evenly, and in October it is further west, and this means that in April the Moon catches up with the Sun relatively late, and in October relatively early. This in turn means that the argument of latitude at the actual time of the eclipse will be raised higher in April and lowered in October. Eclipses (either partial or not) with low inex index (near the upper edge in the "Panorama" graph) fail to occur in April because syzygy occurs too far to the east of the node, but more eclipses occur at high inex values in April because syzygy is not so far west of the node. The opposite applies to October. It also means that in April ascending-node solar eclipses will cast their shadow further north (such as the solar eclipse of April 8, 2024), and descending-node eclipses further south. The opposite is the case in October.

Eclipses that occur when the earth is near perihelion (sun anomaly near zero) are in saros series in which the gamma value changes little every 18.03 years. The reason for this is that from one eclipse to the next in the saros series, the day in the year advances by about 11 days, but the Sun's position moves eastward by more than what it does for that change of day in year at other times. This means the Sun's position relative to the node doesn't change as much as for saros series giving eclipses at other times of the year. In the first half of the 21st century, solar saros series showing this slow rate of change of gamma include 122 (giving an eclipse on January 6, 2019), 132 (January 5, 2038), 141 (January 15, 2010), and 151 (January 4, 2011). Sometimes this phenomenon leads to a saros series giving a large number of central eclipses, for exammple solar saros 128 gave 20 eclipses with |γ|<0.75 between 1615 and 1958, whereas series 135 gave only nine, between 1872 and 2016. ^[14]

The time interval between two eclipses in an eclipse cycle is variable. The time of an eclipse can be advanced or delayed by up to ten hours due to the eccentricity of the Moon's orbit –the eclipse will be early when the Moon is going from perigee to apogee, and late when it is going from apogee toward perigee. The time is also delayed because of the eccentricity of the Earth's orbit. Eclipses occur about four hours later in April and four hours earlier in October. This means that the delay varies from eclipse to eclipse in a series. The delay is the sum of two sine-like functions, one based on the time in the anomalistic year and one on the time in the anomalistic month. The periods of these two waves depends on how close the nominal interval between two eclipses in the series is to a whole number of anomalistic years and anomalistic months. In series like the "Immobilis" or the "Accuratissima", which are near whole numbers of both, the delay varies very slowly, so the interval is quite constant. In series like the octon, the Moon's anomaly changes considerably at least twice every three intervals, so the intervals vary considerably.

The "Panorama" can also be related to where on the Earth the shadow of the Moon falls at the central time of the eclipse. If this "maximum eclipse" for a given eclipse is at a particular location, eclipses three saros later will be at a similar latitude (because the saros is close to a whole number of draconic months) and longitude (because a period of three saros is always within a couple hours of being 19755.96 days long, which would change the longitude by about 13° eastward). If instead we increase the saros index at a constant inex index, the intervals are quite variable because the number of anomalistic months or years is not very close to a whole number. This means that although the latitude will be similar (but changing sign), the longitude change can vary by more than 180°. Moving by six inex (a de la Hire cycle) preserves the latitude fairly well but the longitude change is very variable because of the variation of the solar anomaly.

Both the angular size of the Moon in the sky at eclipses at the ascending node and the size of the Sun at those eclipses vary in a sort of sine wave. The sizes at the descending node vary in the same way, but 180° out of phase. The Moon is large at an ascending-node eclipse when its perigee is near the ascending node, so the period for the size of the Moon is the time it takes for the angle between the node and the perigee to go through 360°, or

${\displaystyle {\frac {1}{1/{\text{period of node}}+1/{\text{period of perigee}}}}={\frac {1}{1/18.60+1/8.85}}=5.997}$ years

(Note that a plus sign is used because the perigee moves eastward whereas the node moves westward.) A maximum of this is in 2024 (September), explaining why the ascending-node solar eclipse of April 8, 2024, is near perigee and total and the descending-node solar eclipse of October 2, 2024, is near apogee and annular. Although this cycle is about a day less than six years, super-moon eclipses actually occur every three years on average, because there are also the ones at the descending node that occur in between the ones at the ascending node. At lunar eclipses the size of the Moon is 180° out of phase with its size at solar eclipses.

The Sun is large at an ascending-node eclipse when its perigee (the direction toward the Sun when it is closest to the Earth) is near the ascending node, so the period for the size of the Sun is

${\displaystyle {\frac {1}{1/{\text{period of node}}-1/{\text{period of perigee}}}}={\frac {1}{1/18.60+1/41{\text{ million}}}}=18.60}$ years

In terms of Delaunay arguments, the Sun is biggest at ascending-node solar eclipses and smallest at descending-node solar eclipses around when l'+D=F (modulo 360°), such as June, 2010. It is smallest at descending-node solar eclipses and biggest at ascending-node solar eclipses 9.3 years later, such as September, 2019.

Long-term trends

The lengths of the synodic, draconic, and anomalistic months, the length of the day, and the length of the anomalistic year are all slowly changing. The synodic and draconic months, the day, and the anomalistic year (at least at present) are getting longer, whereas the anomalistic month is getting shorter. The eccentricity of the Earth's orbit is presently decreasing at about one percent per 300 years, thus decreasing the effect of the sun's anomaly. Formulae for the Delaunay arguments show that the lengthening of the synodic month means that eclipses tend to occur later than they would otherwise proportionally to the square of the time separation from now, by about 0.32 hours per millennium squared. The other Delaunay arguments (mean anomaly of the Moon and of the sun and the argument of latitude) will all be increased because of this, but on the other hand the Delaunay arguments are also affected by the fact that the lengths of the draconic month and anomalistic month and year are changing. The net results are:

• the mean argument of latitude is decreased by 0.16° per millennium squared, corresponding to 0.00045 draconic months
• the mean anomaly of the Moon is increased by 1.1° per millennium squared, corresponding to 0.0030 anomalistic months
• the mean anomaly of the sun is decreased by 0.002° per millennium squared, which is fairly negligible.

As an example, from the solar eclipse of April, 1688 BC, to that of April, AD 1623, is 110 inex plus 7 saros (equivalent to a "Palaea-Horologia" plus a "tritrix", 3310.09 Julian years). According to the table above, the Delaunay arguments should change by:

• 40941 synodic months, 44429.003 draconic months, 43877.032 anomalistic months, 3310.007 anomalistic years, resp.

But because of the changing lengths of these, they actually changed by: ^[22]

• 40940.998 synodic months, 44429.006 draconic months, 43876.990 anomalistic months, 3310.007 anomalistic years, resp.

Note that in this example, in terms of anomaly (position with respect to perigee) the moon returns to within 1% of an orbit (about 3.4°), rather than 3.2% as predicted using today's values of month lengths.

The fact that the day is getting longer means there are more revolutions of the Earth since some point in the past than what one might calculate from the time and date, and fewer from now to some future time. This effect means eclipses occur earlier in the day or calendar, going in the opposite direction relative to the effect of the lengthening synodic month already mentioned. This effect is known as ΔT. It cannot be calculated exactly but amounts to around 50 minutes per millennium squared. ^[24] In our example above, this means that although the eclipse in 1688 BC was centred on March 16 at 00:15:31 in Dynamic time, it actually occurred before midnight and therefore on March 15 (using time based on the location of present-day Greenwich, and using the proleptic Julian calendar). ^[25]

The fact that the argument of latitude is decreased explains why one sees a curvature in the "Panorama" above. Central eclipses in the past and in the future are higher in the graph (lower inex number) than what one would expect from a linear extrapolation. This is because the ratio of the length of a synodic month to the length of a draconic month is getting smaller. Although both are getting longer, the draconic month is doing so more quickly because the rate at which the node moves west is decreasing. ^[22]

See also

• Saros (astronomy)

Related Research Articles

The saros is a period of exactly 223 synodic months, approximately 6585.321 days, or 18 years plus 10, 11, or 12 days, and 8 hours, that can be used to predict eclipses of the Sun and Moon. One saros period after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, a near straight line, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle. A sar is one half of a saros.

The inex is an eclipse cycle of 10,571.95 days. The cycle was first described in modern times by Crommelin in 1901, but was named by George van den Bergh who studied it in detail half a century later. It has been suggested that the cycle was known to Hipparchos. One inex after an eclipse of a particular saros series there will be an eclipse in the next saros series, unless the latter saros series has come to an end.

The Greek astronomer Hipparchus introduced three cycles that have been named after him in later literature.

A total lunar eclipse will take place on Tuesday, March 3, 2026, the first of two lunar eclipses in 2026.

A total lunar eclipse will take place on May 26, 2040. The northern limb of the Moon will pass through the center of the Earth's shadow. This is the second central lunar eclipse of Saros series 131. This lunar event will occur near perigee, as a result, it will be referred to as a "super flower blood moon" or "super blood moon", though not quite as close to Earth as the eclipse of May 26, 2021.

A total lunar eclipse will take place between Monday and Tuesday, June 25-26, 2029. A central total eclipse lasting 1 hour and 41 minutes 53 seconds will plunge the full Moon into deep darkness, as it passes right through the centre of the Earth's umbral shadow. While the visual effect of a total eclipse is variable, the Moon may be stained a deep orange or red color at maximum eclipse. It will be able to be seen from most of the Americas, Western Europe and Africa. The partial eclipse will last for 3 hours and 39 minutes 32 seconds in total.

A total lunar eclipse took place on Friday, August 6, 1971, the second of two total lunar eclipses in 1971. A dramatic total eclipse lasting 1 hour, 39 minutes and 24.8 seconds plunged the full Moon into deep darkness, as it passed right through the centre of the Earth's umbral shadow. While the visual effect of a total eclipse is variable, the Moon may have been stained a deep orange or red colour at maximum eclipse. This was a great spectacle for everyone who saw it. The partial eclipse lasted for 3 hours, 35 minutes and 31.9 seconds in total. Occurring only 2.2 days before perigee, the Moon's apparent diameter was 3.6% larger than average and the moon passed through the center of the Earth's shadow.

A total lunar eclipse took place on Wednesday, May 3, 1939. A shallow total eclipse saw the Moon in relative darkness for 1 hour and 2 minutes. The Moon was 18% of its diameter into the Earth's umbral shadow, and should have been significantly darkened. The partial eclipse lasted for 3 hours and 27 minutes in total.

A total lunar eclipse will take place on June 6, 2058. The Moon will pass through the center of the Earth's shadow.

A total lunar eclipse will take place on May 17, 2087. The moon will pass through the center of the Earth's shadow.

A total lunar eclipse took place at the Moon's descending node of the orbit on Tuesday, May 24, 1910 with an umbral eclipse magnitude of 1.09503. A total lunar eclipse takes place when the Earth comes between the Sun and the Moon and its shadow covers the Moon. Eclipse watchers can see the Moon turn red when the eclipse reaches totality. Total eclipses of the Moon happen at Full Moon when the Sun, Earth, and Moon are aligned to form a line. The astronomical term for this type of alignment is syzygy, which comes from the Greek word for being paired together. The Moon does not have its own light but shines because its surface reflects the Sun's rays. During a total lunar eclipse, the Earth comes between the Sun and the Moon and blocks any direct sunlight from reaching the Moon. The Sun casts the Earth's shadow on the Moon's surface. A shallow total eclipse saw the Moon in relative darkness for 49 minutes and 29.5 seconds. The Moon was 9.503% of its diameter into the Earth's umbral shadow, and should have been significantly darkened. The partial eclipse lasted for 3 hours, 35 minutes and 22.9 seconds in total.

A total lunar eclipse will take place on January 22, 2084.

A total lunar eclipse will take place on May 6, 2069. The eclipse will be dark, with the southern tip of the Moon passing through the center of the Earth's shadow. This is the first central eclipse of Saros series 132.

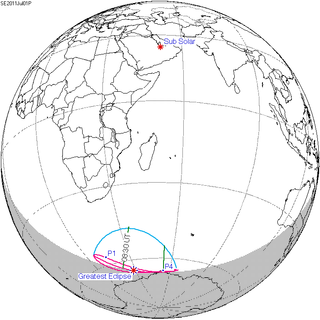
A partial solar eclipse occurred at the Moon’s descending node of orbit on Friday, July 1, 2011, with a magnitude of 0.0971. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

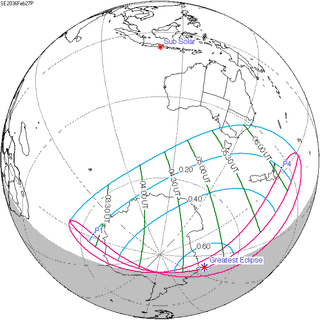
A partial solar eclipse will occur at the Moon's descending node of orbit on Wednesday, February 27, 2036, with a magnitude of 0.6286. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

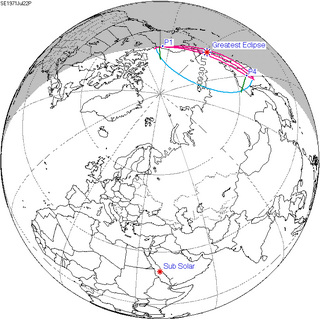
A partial solar eclipse occurred at the Moon's descending node of orbit on Thursday, July 22, 1971, with a magnitude of 0.0689. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

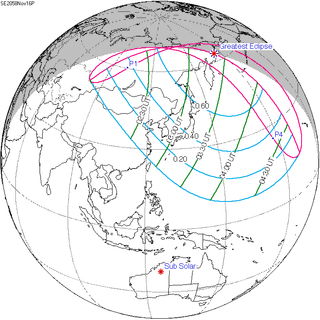
A partial solar eclipse will occur at the Moon's descending node of orbit on Saturday, November 16, 2058, with a magnitude of 0.7644. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

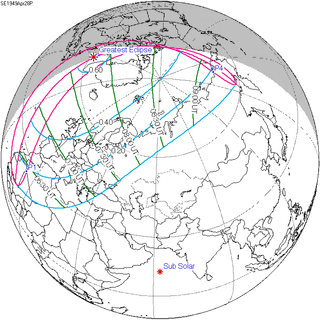
A partial solar eclipse occurred at the Moon's ascending node of orbit on Thursday, April 28, 1949, with a magnitude of 0.6092. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

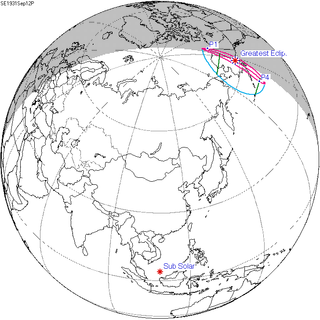
A partial solar eclipse occurred at the Moon's descending node of orbit on Saturday, September 12, 1931, with a magnitude of 0.0471. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

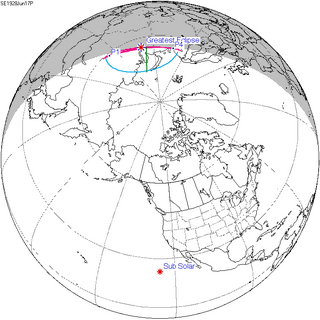
A partial solar eclipse occurred at the Moon's ascending node of orbit on Sunday, June 17, 1928, with a magnitude of 0.0375. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. A partial solar eclipse occurs in the polar regions of the Earth when the center of the Moon's shadow misses the Earth.

References

• S. Newcomb (1882): On the recurrence of solar eclipses. Astron.Pap.Am.Eph. vol. I pt. I . Bureau of Navigation, Navy Dept., Washington 1882
• J.N. Stockwell (1901): Eclips-cycles. Astron.J. 504 [vol.xx1(24)], 14-Aug-1901
• A.C.D. Crommelin (1901): The 29-year eclipse cycle. Observatory xxiv nr.310, 379, Oct-1901
• A. Pannekoek (1951): Periodicities in Lunar Eclipses. Proc. Kon. Ned. Acad. Wetensch. Ser.B vol.54 pp. 30..41 (1951)
• G. van den Bergh (1954): Eclipses in the second millennium B.C. Tjeenk Willink & Zn NV, Haarlem 1954
• G. van den Bergh (1955): Periodicity and Variation of Solar (and Lunar) Eclipses, 2 vols. Tjeenk Willink & Zn NV, Haarlem 1955
• Jean Meeus (1991): Astronomical Algorithms (1st ed.). Willmann-Bell, Richmond VA 1991; ISBN   0-943396-35-2
• Jean Meeus (1997): Mathematical Astronomy Morsels [I], Ch.9 Solar Eclipses: Some Periodicities (pp. 49..55). Willmann-Bell, Richmond VA 1997; ISBN   0-943396-51-4
• Jean Meeus (2004): Mathematical Astronomy Morsels III, Ch.21 Lunar Tetrads (pp. 123..140). Willmann-Bell, Richmond VA 2004; ISBN   0-943396-81-6

External links

• A Catalogue of Eclipse Cycles (more comprehensive than the above)
• Search 5,000 years worth of eclipses between 2000 BC and AD 3000
• Eclipses, Cosmic Clockwork of the Ancients
• The Saros and the Inex