A delicate prime, digitally delicate prime, or weakly prime number is a prime number where, under a given radix but generally decimal, replacing any one of its digits with any other digit always results in a composite number. [1]
A prime number is called a digitally delicate prime number when, under a given radix but generally decimal, replacing any one of its digits with any other digit always results in a composite number. [1] A weakly prime base-b number with n digits must produce composite numbers after every digit is individually changed to every other digit. There are infinitely many weakly prime numbers in any base. Furthermore, for any fixed base there is a positive proportion of such primes. [2]
In 1978, Murray S. Klamkin posed the question of whether these numbers existed. Paul Erdős proved that there exist an infinite number of "delicate primes" under any base. [1]
In 2007, Jens Kruse Andersen found the 1000-digit weakly prime . [3] This is the largest known weakly prime number as of 2011 [update] .
In 2011, Terence Tao proved in a 2011 paper, that delicate primes exist in a positive proportion for all bases. [4] Positive proportion here means as the primes get bigger, the distance between the delicate primes will be quite similar, thus not scarce among prime numbers. [1]
In 2021, Michael Filaseta of the University of South Carolina tried to find a delicate prime number such that when you add an infinite number of leading zeros to the prime number and change any one of its digits, including the leading zeros, it becomes composite. He called these numbers widely digitally delicate. [5] He with a student of his showed in the paper that there exist an infinite number of these numbers, although they could not produce a single example of this, having looked through 1 to 1 billion. They also proved that a positive proportion of primes are widely digitally delicate. [1]
Jon Grantham gave an explicit example of a 4032-digit widely digitally delicate prime. [6]
The smallest weakly prime base-b number for bases 2 through 10 are: [7]
| Base | In base | Decimal |
|---|---|---|
| 2 | 11111112 | 127 |
| 3 | 23 | 2 |
| 4 | 113114 | 373 |
| 5 | 3135 | 83 |
| 6 | 3341556 | 28151 |
| 7 | 4367 | 223 |
| 8 | 141038 | 6211 |
| 9 | 37389 | 2789 |
| 10 | 29400110 | 294001 |
In the decimal number system, the first weakly prime numbers are:
For the first of these, each of the 54 numbers 094001, 194001, 394001, ..., 294009 are composite.
In number theory, a Carmichael number is a composite number , which in modular arithmetic satisfies the congruence relation:
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called numerals; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any number using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels, for ordering, and for codes. In common usage, a numeral is not clearly distinguished from the number that it represents.
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair or (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.
A palindromic number is a number that remains the same when its digits are reversed. In other words, it has reflectional symmetry across a vertical axis. The term palindromic is derived from palindrome, which refers to a word whose spelling is unchanged when its letters are reversed. The first 30 palindromic numbers are:
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1 — a more specific type of repdigit. The term stands for "repeated unit" and was coined in 1966 by Albert H. Beiler in his book Recreations in the Theory of Numbers.
In recreational mathematics, a repdigit or sometimes monodigit is a natural number composed of repeated instances of the same digit in a positional number system. The word is a portmanteau of "repeated" and "digit". Examples are 11, 666, 4444, and 999999. All repdigits are palindromic numbers and are multiples of repunits. Other well-known repdigits include the repunit primes and in particular the Mersenne primes.
Quaternary is a numeral system with four as its base. It uses the digits 0, 1, 2, and 3 to represent any real number. Conversion from binary is straightforward.
Positional notation usually denotes the extension to any base of the Hindu–Arabic numeral system. More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred. In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string.
In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured that every set of integers A with positive natural density contains a k-term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.
Ben Joseph Green FRS is a British mathematician, specialising in combinatorics and number theory. He is the Waynflete Professor of Pure Mathematics at the University of Oxford.
In mathematics, a prime number p is called a Chen prime if p + 2 is either a prime or a product of two primes. The even number 2p + 2 therefore satisfies Chen's theorem.
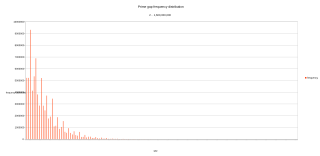
A prime gap is the difference between two successive prime numbers. The n-th prime gap, denoted gn or g(pn) is the difference between the (n + 1)-st and the n-th prime numbers, i.e.
At the 1912 International Congress of Mathematicians, Edmund Landau listed four basic problems about prime numbers. These problems were characterised in his speech as "unattackable at the present state of mathematics" and are now known as Landau's problems. They are as follows:
In number theory, the Green–Tao theorem, proved by Ben Green and Terence Tao in 2004, states that the sequence of prime numbers contains arbitrarily long arithmetic progressions. In other words, for every natural number k, there exist arithmetic progressions of primes with k terms. The proof is an extension of Szemerédi's theorem. The problem can be traced back to investigations of Lagrange and Waring from around 1770.
In number theory, primes in arithmetic progression are any sequence of at least three prime numbers that are consecutive terms in an arithmetic progression. An example is the sequence of primes, which is given by for .
In mathematics, arithmetic combinatorics is a field in the intersection of number theory, combinatorics, ergodic theory and harmonic analysis.
James Alexander Maynard is an English mathematician working in analytic number theory and in particular the theory of prime numbers. In 2017, he was appointed Research Professor at Oxford. Maynard is a fellow of St John's College, Oxford. He was awarded the Fields Medal in 2022 and the New Horizons in Mathematics Prize in 2023.
