Mathematics

Nineteen is the eighth prime number.
Number theory
19 forms a twin prime with 17, [1] a cousin prime with 23, [2] and a sexy prime with 13. [3] 19 is the fifth central trinomial coefficient, [4] and the maximum number of fourth powers needed to sum up to any natural number (see, Waring's problem). [5] It is the number of compositions of 8 into distinct parts. [6]
19 is the eighth strictly non-palindromic number in any base, following 11 and preceding 47. [7] 19 is also the second octahedral number, after 6, [8] and the sixth Heegner number.
In the Engel expansion of pi, [9] 19 is the seventh term following {1, 1, 1, 8, 8, 17} and preceding {300, 1991, ...}. The sum of the first terms preceding 17 is in equivalence with 19, where its prime index (8) are the two previous members in the sequence.
Prime properties
19 is the seventh Mersenne prime exponent. [10] It is the second Keith number, and more specifically the first Keith prime. [11] In decimal, 19 is the third full reptend prime, [12] and the first prime number that is not a permutable prime, as its reverse (91) is composite (where 91 is also the fourth centered nonagonal number). [13]
- 19 × 91 = 1729, the first Hardy-Ramanujan number or taxicab number, also a Harshad number in base-ten, as it's divisible by the sum of its digits, 19. [14] [15]
- 1729 is also the nineteenth dodecagonal number. [16]
19, alongside 109, 1009, and 10009, are all prime (with 109 also full reptend), and form part of a sequence of numbers where inserting a digit inside the previous term produces the next smallest prime possible, up to scale, with the composite number 9 as root. [17] 100019 is the next such smallest prime number, by the insertion of a 1.
- Numbers of the form 10n9 equivalent to 10x + 9 with x = n + 1, where n is the number of zeros in the term, are prime for n = {0, 1, 2, 3, 8, 17, 21, 44, 48, 55, 68, 145, 201, 271, 2731, 4563}, and probably prime for n = {31811, 43187, 48109, 92691}. [18]
Otherwise, is the second base-10 repunit prime, short for the number . [19]
The sum of the squares of the first nineteen primes is divisible by 19. [20]
Figurate numbers and magic figures
19 is the third centered triangular number as well as the third centered hexagonal number. [21] [22]
- The 19th triangular number is 190, equivalently the sum of the first 19 non-zero integers, that is also the sixth centered nonagonal number. [23] [13]
- 19 is the first number in an infinite sequence of numbers in decimal whose digits start with 1 and have trailing 9's, that form triangular numbers containing trailing zeroes in proportion to 9s present in the original number; i.e. 19900 is the 199th triangular number, and 1999000 is the 1999th. [24]
- Like 19, 199 and 1999 are also both prime, as are 199999 and 19999999. In fact, a number of the form 19n, where n is the number of nines that terminate in the number, is prime for:
- n = {1, 2, 3, 5, 7, 26, 27, 53, 147, 236, 248, 386, 401}. [25]
The number of nodes in regular hexagon with all diagonals drawn is nineteen. [26]
- Distinguishably, the only nontrivial normal magic hexagon is composed of nineteen cells, where every diagonal of consecutive hexagons has sums equal to 38, or twice 19. [27]
- A hexaflexagon is a strip of nineteen alternating triangular faces that can flex into a regular hexagon, such that any two of six colorings on triangles can be oriented to align on opposite sides of the folded figure. [28]
- Nineteen is also the number of one-sided hexiamonds, meaning there are nineteen ways of arranging six equiangular triangular polyforms edge-to-edge on the plane without turn-overs (and where holes are allowed). [29]
can be used to generate the first full, non-normal prime reciprocal magic square in decimal whose rows, columns and diagonals — in a 18 x 18 array — all generate a magic constant of 81 = 92. [30]
- The next prime number to generate a like-magic square in base-ten is 383, [31] the seventy-sixth prime number (where 19 × 4 = 76). [32] A regular 19 x 19 magic square, on the other hand, has a magic constant of 3439 = 19 × 181. [33]
Collatz problem
The Collatz sequence for nine requires nineteen steps to return to one, more than any other number below it. [34] On the other hand, nineteen requires twenty steps, like eighteen. Less than ten thousand, only thirty-one other numbers require nineteen steps to return to one:
- {56, 58, 60, 61, 352, 360, 362, 368, 369, 372, 373, 401, 402, 403, 2176, ..., and 2421}. [35]
In abstract algebra
The projective special linear group represents the abstract structure of the 57-cell: a universal 4-polytope with a total of one hundred and seventy-one (171 = 9 × 19) edges and vertices, and fifty-seven (57 = 3 × 19) hemi-icosahedral cells that are self-dual. [36]
In total, there are nineteen Coxeter groups of non-prismatic uniform honeycombs in the fourth dimension: five Coxeter honeycomb groups exist in Euclidean space, while the other fourteen Coxeter groups are compact and paracompact hyperbolic honeycomb groups.
- There are also specifically nineteen uniform honeycombs inside the Euclidean tesseractic honeycomb group in 4-space. In 5-space, there are nineteen uniform polytopes with simplex symmetry.
There are infinitely many finite-volume Vinberg polytopes up through dimension nineteen, which generate hyperbolic tilings with degenerate simplex quadrilateral pyramidal domains, as well as prismatic domains and otherwise. [37]
- Vinberg polytopes of lowest rank n + 2 mirrors exist up through the seventeenth dimension, where there exists a unique figure with nineteen facets. [38] It is expressed with the simple Dynkin diagram,




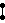























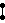



 .
.
On the other hand, a cubic surface is the zero set in of a homogeneous cubic polynomial in four variables a polynomial with a total of twenty coefficients, which specifies a space for cubic surfaces that is 19-dimensional. [39]
Finite simple groups
19 is the eighth consecutive supersingular prime . It is the middle indexed member in the sequence of fifteen such primes that divide the order of the Friendly Giant , the largest sporadic group: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71}. [40]
- Janko groups and are the two-smallest of six pariah groups that are not subquotients of , which contain 19 as the largest prime number that divides their orders. [41]
- holds (2,3,7) as standard generators (a,b,ab) that yield a semi-presentation where o(abab2) = 19, while holds as standard generators (2A, 3A, 19), where o([a, b]) = 9. [42] [43]
- is the dimensionality of the minimal faithful complex representation of O'Nan group — the second-largest after of like-representation in and largest amongst the six pariahs [44] — whose value lies midway between primes (10939, 10949), the latter with a prime index of , [45] which is the nineteenth tetrahedral number. [46]
- On the other hand, the Tits group , as the only non-strict group of Lie type that can loosely categorize as sporadic, has group order 211 · 33 · 52 · 13, whose prime factors (inclusive of powers) generate a sum equal to 54 , which is the smallest non-trivial 19-gonal number. [47]
In the Happy Family of sporadic groups, nineteen of twenty-six such groups are subquotients of the Friendly Giant, which is also its own subquotient. [48] If the Tits group is indeed included as a group of Lie type, [49] then there are nineteen classes of finite simple groups that are not sporadic groups.
Worth noting, 26 is the only number to lie between a perfect square (52) and a cube (33); if all primes in the prime factorizations of 25 and 27 are added together, a sum of 19 is obtained.
Heegner number
19 is the sixth Heegner number . [50] 67 and 163, respectively the 19th and 38th prime numbers, are the two largest Heegner numbers, of nine total.
The sum of the first six Heegner numbers 1, 2, 3, 7, 11, and 19 sum to the seventh member and fourteenth prime number, 43. All of these numbers are prime, aside from the unit. In particular, 163 is relevant in moonshine theory.



















