
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e., an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral. Its dual polyhedron is the rhombic dodecahedron.
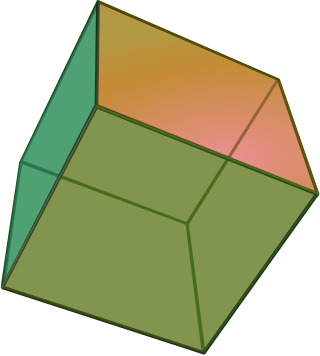
In geometry, a cube or regular hexahedron is a three-dimensional solid object bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.
In geometry, an octahedron is a polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. Many types of irregular octahedra also exist, including both convex and non-convex shapes.

In geometry, the rhombicuboctahedron is an Archimedean solid with 26 faces, consisting of 8 equilateral triangles and 18 squares. It was named by Johannes Kepler in his 1618 Harmonices Mundi, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron.

In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices. Kepler first named it in Latin as cubus simus in 1619 in his Harmonices Mundi. H. S. M. Coxeter, noting it could be derived equally from the octahedron as the cube, called it snub cuboctahedron, with a vertical extended Schläfli symbol , and representing an alternation of a truncated cuboctahedron, which has Schläfli symbol .
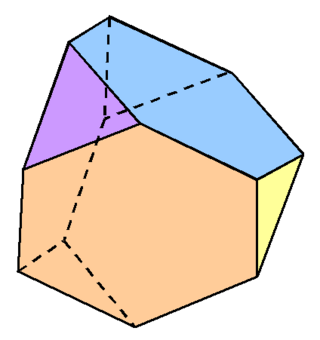
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 equilateral triangle faces, 12 vertices and 18 edges. It can be constructed by truncating all 4 vertices of a regular tetrahedron.

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces, 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate 3-dimensional space, as a permutohedron.

In geometry, the rhombicosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.

In geometry, the truncated cuboctahedron or great rhombicuboctahedron is an Archimedean solid, named by Kepler as a truncation of a cuboctahedron. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices, and 72 edges. Since each of its faces has point symmetry, the truncated cuboctahedron is a 9-zonohedron. The truncated cuboctahedron can tessellate with the octagonal prism.

In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron or omnitruncated icosahedron is an Archimedean solid, one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces.

In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.
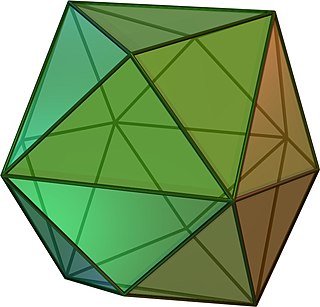
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it.

In four-dimensional geometry, a runcinated tesseract is a convex uniform 4-polytope, being a runcination of the regular tesseract.
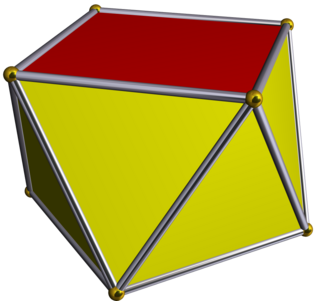
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.




















































































































