Pyramid (geometry)

Last updated

In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, or cutting off the apex. It can be generalized into higher dimension, known as hyperpyramid. All pyramids are self-dual.

Contents

Etymology

The word "pyramid" derives from the ancient Greek term "πυραμίς" (pyramis), which referred to a pyramid-shaped structure and a type of wheat cake. [1] [2] The term is rooted in the Greek "πυρ" (pyr, 'fire') and "άμις" (amis, 'vessel'), highlighting the shape's pointed, flame-like appearance. [3]

In Byzantine Greek, the term evolved to "πυραμίδα" (pyramída), continuing to denote pyramid structures. [4] The Greek term "πυραμίς" was borrowed into Latin as "pyramis." The term "πυραμίδα" influenced the evolution of the word into "pyramid" in English and other languages. [5] [6]

Definition

Parts of a pyramid Pyramid.svg
Parts of a pyramid

A pyramid is a polyhedron that may be formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form an isosceles triangle, called a lateral face. [7] The edges connected from the polygonal base's vertices to the apex are called lateral edges. [8] Historically, the definition of a pyramid has been described by many mathematicians in ancient times. Euclides in his Elements defined a pyramid as a solid figure, constructed from one plane to one point. The context of his definition was vague until Heron of Alexandria defined it as the figure by putting the point together with a polygonal base. [9]

A prismatoid is defined as a polyhedron where its vertices lie on two parallel planes, with its lateral faces are triangles, trapezoids, and parallelograms. [10] Pyramids are classified as prismatoid. [11]

Classification and types

Tetrahedron.svg
Square pyramid.png
Pentagonal pyramid.png
Hexagonal pyramid.png
The family of a regular polygonal base pyramid: tetrahedron, square pyramid, pentagonal pyramid, and hexagonal pyramid.

A right pyramid is a pyramid where the base is circumscribed about the circle and the altitude of the pyramid meets at the circle's center. [12] This pyramid may be classified based on the regularity of its bases. A pyramid with a regular polygon as the base is called a regular pyramid. [13] For the pyramid with an n-sided regular base, it has n + 1 vertices, n + 1 faces, and 2n edges. [14] Such pyramid has isosceles triangles as its faces, with its symmetry is Cnv, a symmetry of order 2n: the pyramids are symmetrical as they rotated around their axis of symmetry (a line passing through the apex and the base centroid), and they are mirror symmetric relative to any perpendicular plane passing through a bisector of the base. [15] [16] Examples are square pyramid and pentagonal pyramid, a four- and five-triangular faces pyramid with a square and pentagon base, respectively; they are classified as the first and second Johnson solid if their regular faces and edges that are equal in length, and their symmetries are C4v of order 8 and C5v of order 10, respectively. [17] [18] A tetrahedron or triangular pyramid is an example that has four equilateral triangles, with all edges equal in length, and one of them is considered as the base. Because the faces are regular, it is an example of a Platonic solid and deltahedra, and it has tetrahedral symmetry. [19] [20] A pyramid with the base as circle is known as cone. [21] Pyramids have the property of self-dual, meaning their duals are the same as vertices corresponding to the edges and vice versa. [22] Their skeleton may be represented as the wheel graph. [23]

Rectangular right pyramid.png
Rhombic right pyramid.png
Pyramids with rectangular and rhombic bases

A right pyramid may also have a base with an irregular polygon. Examples are the pyramids with rectangle and rhombus as their bases. These two pyramids have the symmetry of C2v of order 4.

Cono truncado.svg
A pyramid truncated by an inclined plane
Pentagram pyramid.png
A pentagram-base pyramid.

The type of pyramids can be derived in many ways. The base regularity of a pyramid's base may be classified based on the type of polygon, and one example is the pyramid with regular star polygon as its base, known as the star pyramid. [24] The pyramid cut off by a plane is called a truncated pyramid; if the truncation plane is parallel to the base of a pyramid, it is called a frustum.

Mensuration

The surface area is the total area of each polyhedra's faces. In the case of a pyramid, its surface area is the sum of the area of triangles and the area of the polygonal base.

The volume of a pyramid is the one-third product of the base's area and the height. Given that is the base's area and is the height of a pyramid. Mathematically, the volume of a pyramid is: [25] The volume of a pyramid was recorded back in ancient Egypt, where they calculated the volume of a square frustum, suggesting they acquainted the volume of a square pyramid. [26] The formula of volume for a general pyramid was discovered by Indian mathematician Aryabhata, where he quoted in his Aryabhatiya that the volume of a pyramid is incorrectly the half product of area's base and the height. [27]

Generalization

4-dimensional hyperpyramid with a cube as base Hyperpyramide-animation.gif
4-dimensional hyperpyramid with a cube as base

The hyperpyramid is the generalization of a pyramid in n-dimensional space. In the case of the pyramid, one connects all vertices of the base, a polygon in a plane, to a point outside the plane, which is the peak. The pyramid's height is the distance of the peak from the plane. This construction gets generalized to n dimensions. The base becomes a (n − 1)-polytope in a (n − 1)-dimensional hyperplane. A point called the apex is located outside the hyperplane and gets connected to all the vertices of the polytope and the distance of the apex from the hyperplane is called height. [28]

The n-dimensional volume of a n-dimensional hyperpyramid can be computed as follows: Here Vn denotes the n-dimensional volume of the hyperpyramid. A denotes the (n − 1)-dimensional volume of the base and h the height, that is the distance between the apex and the (n − 1)-dimensional hyperplane containing the base A. [28]

Related Research Articles

In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usually coplanar and a bipyramid is usually symmetric, meaning the two pyramids are mirror images across their common base plane. When each apex of the bipyramid is on a line perpendicular to the base and passing through its center, it is a right bipyramid; otherwise it is oblique. When the base is a regular polygon, the bipyramid is also called regular.

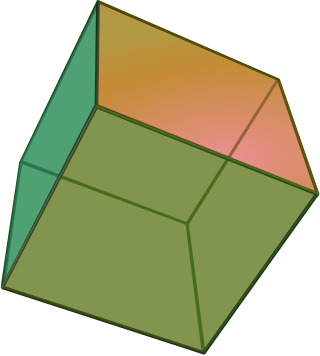
<span class="mw-page-title-main">Cube</span> Solid object with six equal square faces

In geometry, a cube is a three-dimensional solid object bounded by six square faces. It has twelve edges and eight vertices. It can be represented as a rectangular cuboid with six square faces, or a parallelepiped with equal edges. It is an example of many type of solids: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron.

<span class="mw-page-title-main">Regular icosahedron</span> Convex polyhedron with 20 triangular faces

In geometry, the regular icosahedron is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the skeleton of a regular icosahedron.

<span class="mw-page-title-main">Icosidodecahedron</span> Archimedean solid with 32 faces

In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (icosi) triangular faces and twelve (dodeca) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.

In geometry, an octahedron is a polyhedron with eight faces. An octahedron can be considered as a square bipyramid. When the edges of a square bipyramid are all equal in length, it produces a regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. It is also an example of a deltahedron. An octahedron is the three-dimensional case of the more general concept of a cross polytope.

<span class="mw-page-title-main">Polyhedron</span> 3D shape with flat faces, straight edges and sharp corners

In geometry, a polyhedron is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices.

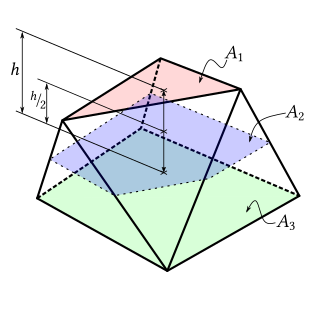
<span class="mw-page-title-main">Prismatoid</span> Polyhedron with all vertices in two parallel planes

In geometry, a prismatoid is a polyhedron whose vertices all lie in two parallel planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid.

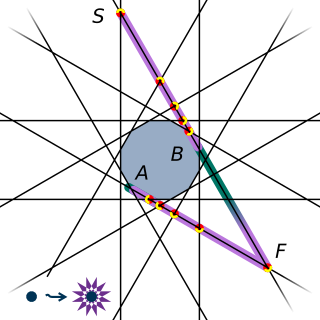
<span class="mw-page-title-main">Stellation</span> Extending the elements of a polytope to form a new figure

In geometry, stellation is the process of extending a polygon in two dimensions, a polyhedron in three dimensions, or, in general, a polytope in n dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word stellation comes from the Latin stellātus, "starred", which in turn comes from the Latin stella, "star". Stellation is the reciprocal or dual process to faceting.

<span class="mw-page-title-main">Prism (geometry)</span> Solid with 2 parallel n-gonal bases connected by n parallelograms

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

<span class="mw-page-title-main">Regular polytope</span> Polytope with highest degree of symmetry

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.

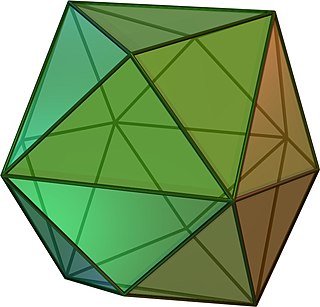
<span class="mw-page-title-main">Tetrakis hexahedron</span> Catalan solid with 24 faces

In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.

<span class="mw-page-title-main">Triaugmented triangular prism</span> Convex polyhedron with 14 triangle faces

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.

<span class="mw-page-title-main">Pentagonal bipyramid</span> Two pentagonal pyramids joined at the bases

In geometry, the pentagonal bipyramid is a polyhedron with 10 triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid.

<span class="mw-page-title-main">Vertex figure</span> Shape made by slicing off a corner of a polytope

In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.

<span class="mw-page-title-main">Pentagonal pyramid</span> Pyramid with a pentagon base

In geometry, pentagonal pyramid is a pyramid with a pentagon base and five triangular faces, having a total of six faces. It is categorized as Johnson solid if all of the edges are equal in length, forming equilateral triangular faces and a regular pentagonal base. The pentagonal pyramid can be found in many polyhedrons, including their construction. It also occurs in stereochemistry in pentagonal pyramidal molecular geometry.

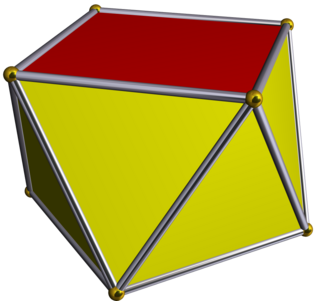
<span class="mw-page-title-main">Uniform polyhedron</span> Isogonal polyhedron with regular faces

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular, quasi-regular, or semi-regular. The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

<span class="mw-page-title-main">Triangular prism</span> Prism with a 3-sided base

In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

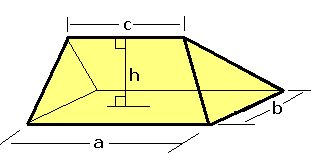
<span class="mw-page-title-main">Wedge (geometry)</span> Polyhedron defined by two triangles and three trapezoid faces

In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.

<span class="mw-page-title-main">Hyperpyramid</span>

A hyperpyramid is a generalisation of the normal pyramid to n dimensions.

References

  1. ↑ "Henry George Liddell, Robert Scott, A Greek-English Lexicon, πυραμίς", www.perseus.tufts.edu.
  2. ↑ The word meant "a kind of cake of roasted wheat-grains preserved in honey"; the Egyptian pyramids were named after its form. See Beekes, Robert S. (2009), Etymological Dictionary of Greek, Brill, p. 1261.
  3. ↑ Liddell, Henry George; Scott, Robert (1940). A Greek–English Lexicon. Clarendon Press.
  4. ↑ "πυραμίδα". Wiktionary. 12 July 2022. Retrieved 30 June 2024.
  5. ↑ Lewis, Charlton T.; Short, Charles (1879). A Latin Dictionary. Clarendon Press.
  6. ↑ Peck, Harry Thurston (1898). Harper's Dictionary of Classical Antiquities. Harper & Brothers.
  7. ↑ Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press, p. 13.
  8. ↑ Smith, James T. (2000), Methods of Geometry, John Wiley & Sons, p. 98, ISBN   0-471-25183-6 .
  9. ↑ Heath, Thomas (1908), Euclid: The Thirteen Books of the Elements, vol. 3, Cambridge University Press, p. 268.
  10. ↑ Alsina, Claudi; Nelsen, Roger B. (2015), A Mathematical Space Odyssey: Solid Geometry in the 21st Century, Mathematical Association of America, p. 85, ISBN   978-0-88385-358-0 .
  11. ↑ Grünbaum, Branko (1997), "Isogonal Prismatoids", Discrete & Computational Geometry, 18: 13–52, doi:10.1007/PL00009307 .
  12. ↑ Polya, G. (1954), Mathematics and Plausible Reasoning: Induction and analogy in mathematics, Princeton University Press, p. 138, ISBN   0-691-02509-6 .
  13. ↑ O'Leary, Michael (2010), Revolutions of Geometry, John Wiley & Sons, p. 10, ISBN   978-0-470-59179-6 .
  14. ↑ Humble, Steve (2016), The Experimenter's A-Z of Mathematics: Math Activities with Computer Support, Taylor & Francis, p. 23, ISBN   978-1-134-13953-8 .
  15. ↑ Johnson, Norman W. (2018), Geometries and Transformations, Cambridge University Press, ISBN   978-1-107-10340-5 . See Chapter 11: Finite Symmetry Groups, 11.3 Pyramids, Prisms, and Antiprisms.
  16. ↑ Alexandroff, Paul (2012), An Introduction to the Theory of Groups, Dover Publications, p. 48, ISBN   978-0-486-48813-4 .
  17. ↑ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics , 18: 169–200, doi: 10.4153/cjm-1966-021-8 , MR   0185507, S2CID   122006114, Zbl   0132.14603 . See table III, line 1.
  18. ↑ Uehara, Ryuhei (2020), Introduction to Computational Origami: The World of New Computational Geometry, Springer, p. 62, doi:10.1007/978-981-15-4470-5, ISBN   978-981-15-4470-5 .
  19. ↑ Shavinina, Larisa V. (2013), The Routledge International Handbook of Innovation Education, Routledge, p. 333, ISBN   978-0-203-38714-6 .
  20. ↑ Cundy, H. Martyn (1952), "Deltahedra", The Mathematical Gazette, 36 (318): 263–266, doi:10.2307/3608204, JSTOR   3608204, S2CID   250435684 .
  21. ↑ Kelley, W. Michael (2009), The Humongous Book of Geometry Problems, Penguin Group, p. 455, ISBN   978-1-61564-698-2 .
  22. ↑ Wohlleben, Eva (2019), "Duality in Non-Polyhedral Bodies Part I: Polyliner", in Cocchiarella, Luigi (ed.), ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary - Milan, Italy, August 3-7, 2018, Advances in Intelligent Systems and Computing, vol. 809, Springer, p. 485–486, doi:10.1007/978-3-319-95588-9, ISBN   978-3-319-95588-9
  23. ↑ Pisanski, Tomaž; Servatius, Brigitte (2013), Configuration from a Graphical Viewpoint, Springer, p. 21, doi:10.1007/978-0-8176-8364-1, ISBN   978-0-8176-8363-4 .
  24. ↑ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 50, ISBN   978-0-521-09859-5, archived from the original on 2013-12-11
  25. ↑ Alexander, Daniel C.; Koeberlin, Geralyn M. (2014), Elementary Geometry for College Students (6th ed.), Cengage Learning, p. 403, ISBN   978-1-285-19569-8 .
  26. ↑ Gillings, R. J. (1964), "The volume of a truncated pyramid in ancient Egyptian papyri", The Mathematics Teacher, 57 (8): 552–555, doi:10.5951/MT.57.8.0552, JSTOR   27957144 .
  27. ↑ Cajori, Florian (1991), History of Mathematics (5th ed.), American Mathematical Society, p. 87, ISBN   978-1-4704-7059-3 .
  28. 1 2 Mathai, A. M. (1999), An Introduction to Geometrical Probability: Distributional Aspects with Applications, Taylor & Francis, p. 42–43, ISBN   978-90-5699-681-9 .

See also

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.