Antiprism

Last updated September 05, 2024

In geometry, an $n$ -gonal antiprism or $n$ -antiprism is a polyhedron composed of two parallel direct copies (not mirror images) of an $n$ -sided polygon, connected by an alternating band of $2 n$ triangles. They are represented by the Conway notation $A n$ .

History

In his 1619 book Harmonices Mundi , Johannes Kepler observed the existence of the infinite family of antiprisms.^[1] This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556.^[2]

The German form of the word "antiprism" was used for these shapes in the 19th century; Karl Heinze credits its introduction to Theodor Wittstein [ de ].^[3] Although the English "anti-prism" had been used earlier for an optical prism used to cancel the effects of a primary optimal element,^[4] the first use of "antiprism" in English in its geometric sense appears to be in the early 20th century in the works of H. S. M. Coxeter.^[5]

Special cases

Right antiprism

For an antiprism with regular $n$ -gon bases, one usually considers the case where these two copies are twisted by an angle of $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠180/n⁠$ degrees.

The axis of a regular polygon is the line perpendicular to the polygon plane and lying in the polygon centre.

For an antiprism with congruent regular $n$ -gon bases, twisted by an angle of $⁠ 180 / n ⁠$ degrees, more regularity is obtained if the bases have the same axis: are coaxial ; i.e. (for non-coplanar bases): if the line connecting the base centers is perpendicular to the base planes. Then the antiprism is called a right antiprism, and its $2 n$ side faces are isosceles triangles.

Uniform antiprism

A uniform $n$ -antiprism has two congruent regular $n$ -gons as base faces, and $2 n$ equilateral triangles as side faces.

Uniform antiprisms form an infinite class of vertex-transitive polyhedra, as do uniform prisms. For $n = 2$ , we have the digonal antiprism (degenerate antiprism), which is visually identical to the regular tetrahedron; for $n = 3$ , the regular octahedron as a triangular antiprism (non-degenerate antiprism).

Family of uniform n-gonal antiprisms
v
t
e
Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	...	Apeirogonal antiprism
Polyhedron image							...
Spherical tiling image							Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

The Schlegel diagrams of these semiregular antiprisms are as follows:

A3	A4	A5	A6	A7	A8

Cartesian coordinates

Cartesian coordinates for the vertices of a right $n$ -antiprism (i.e. with regular $n$ -gon bases and $2 n$ isosceles triangle side faces, circumradius of the bases equal to 1) are:

\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)

where $0 \leq k \leq 2 n - 1$ ;

if the $n$ -antiprism is uniform (i.e. if the triangles are equilateral), then: $2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.$

Volume and surface area

Let $a$ be the edge-length of a uniform $n$ -gonal antiprism; then the volume is: $V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},$

and the surface area is: $A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.$

Furthermore, the volume of a regular right $n$ -gonal antiprism with side length of its bases $l$ and height $h$ is given by: $V={\frac {nhl^{2}}{12}}\left(\csc {\frac {\pi }{n}}+2\cot {\frac {\pi }{n}}\right).$

Derivation

The circumradius of the horizontal circumcircle of the regular $n$ -gon at the base is

R(0)={\frac {l}{2\sin {\frac {\pi }{n}}}}.

The vertices at the base are at

\left({\begin{array}{c}R(0)\cos {\frac {2\pi m}{n}}\\R(0)\sin {\frac {2\pi m}{n}}\\0\end{array}}\right),\quad m=0..n-1;

the vertices at the top are at

\left({\begin{array}{c}R(0)\cos {\frac {2\pi (m+1/2)}{n}}\\R(0)\sin {\frac {2\pi (m+1/2)}{n}}\\h\end{array}}\right),\quad m=0..n-1.

Via linear interpolation, points on the outer triangular edges of the antiprism that connect vertices at the bottom with vertices at the top are at

\left({\begin{array}{c}{\frac {R(0)}{h}}[(h-z)\cos {\frac {2\pi m}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(h-z)\sin {\frac {2\pi m}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1

and at

\left({\begin{array}{c}{\frac {R(0)}{h}}[(h-z)\cos {\frac {2\pi (m+1)}{n}}+z\cos {\frac {\pi (2m+1)}{n}}]\\{\frac {R(0)}{h}}[(h-z)\sin {\frac {2\pi (m+1)}{n}}+z\sin {\frac {\pi (2m+1)}{n}}]\\\\z\end{array}}\right),\quad 0\leq z\leq h,m=0..n-1.

By building the sums of the squares of the $x$ and $y$ coordinates in one of the previous two vectors, the squared circumradius of this section at altitude $z$ is

R(z)^{2}={\frac {R(0)^{2}}{h^{2}}}[h^{2}-2hz+2z^{2}+2z(h-z)\cos {\frac {\pi }{n}}].

The horizontal section at altitude $0\leq z\leq h$ above the base is a $2n$ -gon (truncated $n$ -gon) with $n$ sides of length $l_{1}(z)=l(1-z/h)$ alternating with $n$ sides of length $l_{2}(z)=lz/h$ . (These are derived from the length of the difference of the previous two vectors.) It can be dissected into $n$ isoceless triangles of edges $R(z),R(z)$ and $l_{1}$ (semiperimeter $R(z)+l_{1}(z)/2$ ) plus $n$ isoceless triangles of edges $R(z),R(z)$ and $l_{2}(z)$ (semiperimeter $R(z)+l_{2}(z)/2$ ). According to Heron's formula the areas of these triangles are

Q_{1}(z)={\frac {R(0)^{2}}{h^{2}}}(h-z)\left[(h-z)\cos {\frac {\pi }{n}}+z\right]\sin {\frac {\pi }{n}}

and

Q_{2}(z)={\frac {R(0)^{2}}{h^{2}}}z\left[z\cos {\frac {\pi }{n}}+h-z\right]\sin {\frac {\pi }{n}}.

The area of the section is $n[Q_{1}(z)+Q_{2}(z)]$ , and the volume is

V=n\int _{0}^{h}[Q_{1}(z)+Q_{2}(z)]dz={\frac {nh}{3}}R(0)^{2}\sin {\frac {\pi }{n}}(1+2\cos {\frac {\pi }{n}})={\frac {nh}{12}}l^{2}{\frac {1+2\cos {\frac {\pi }{n}}}{\sin {\frac {\pi }{n}}}}.

Note that the volume of a right $n$ -gonal prism with the same $l$ and $h$ is: $V_{\mathrm {prism} }={\frac {nhl^{2}}{4}}\cot {\frac {\pi }{n}}$ which is smaller than that of an antiprism.

Symmetry

The symmetry group of a right $n$ -antiprism (i.e. with regular bases and isosceles side faces) is $D n d = D n v$ of order $4 n$ , except in the cases of:

$n = 2$ : the regular tetrahedron, which has the larger symmetry group $T d$ of order $24 = 3 \times (4 \times 2)$ , which has three versions of $D 2d$ as subgroups;

$n = 3$ : the regular octahedron, which has the larger symmetry group $O h$ of order $48 = 4 \times (4 \times 3)$ , which has four versions of $D 3d$ as subgroups.

The symmetry group contains inversion if and only if $n$ is odd.

The rotation group is $D n$ of order $2 n$ , except in the cases of:

$n = 2$ : the regular tetrahedron, which has the larger rotation group $T$ of order $12 = 3 \times (2 \times 2)$ , which has three versions of $D 2$ as subgroups;

$n = 3$ : the regular octahedron, which has the larger rotation group $O$ of order $24 = 4 \times (2 \times 3)$ , which has four versions of $D 3$ as subgroups.

Note: The right $n$ -antiprisms have congruent regular $n$ -gon bases and congruent isosceles triangle side faces, thus have the same (dihedral) symmetry group as the uniform $n$ -antiprism, for $n \geq 4$ .

Generalizations

In higher dimensions

Four-dimensional antiprisms can be defined as having two dual polyhedra as parallel opposite faces, so that each three-dimensional face between them comes from two dual parts of the polyhedra: a vertex and a dual polygon, or two dual edges. Every three-dimensional convex polyhedron is combinatorially equivalent to one of the two opposite faces of a four-dimensional antiprism, constructed from its canonical polyhedron and its polar dual.^[6] However, there exist four-dimensional polychora that cannot be combined with their duals to form five-dimensional antiprisms.^[7]

Self-crossing polyhedra

3/2-antiprism nonuniform	5/4-antiprism nonuniform	5/2-antiprism	5/3-antiprism
9/2-antiprism	9/4-antiprism	9/5-antiprism

This shows all the non-star and star antiprisms up to 15 sides, together with those of a 29-agon. Antiprisms.pdf — This shows all the non-star and star antiprisms up to 15 sides, together with those of a 29-agon.

Uniform star antiprisms are named by their star polygon bases, ${p / q},$ and exist in prograde and in retrograde (crossed) solutions. Crossed forms have intersecting vertex figures, and are denoted by "inverted" fractions: $p /(p - q)$ instead of $p / q$ ; example: 5/3 instead of 5/2.

A right star antiprism has two congruent coaxial regular convex or star polygon base faces, and $2 n$ isosceles triangle side faces.

Any star antiprism with regular convex or star polygon bases can be made a right star antiprism (by translating and/or twisting one of its bases, if necessary).

In the retrograde forms, but not in the prograde forms, the triangles joining the convex or star bases intersect the axis of rotational symmetry. Thus:

Retrograde star antiprisms with regular convex polygon bases cannot have all equal edge lengths, and so cannot be uniform. "Exception": a retrograde star antiprism with equilateral triangle bases (vertex configuration: 3.3/2.3.3) can be uniform; but then, it has the appearance of an equilateral triangle: it is a degenerate star polyhedron.

Similarly, some retrograde star antiprisms with regular star polygon bases cannot have all equal edge lengths, and so cannot be uniform. Example: a retrograde star antiprism with regular star 7/5-gon bases (vertex configuration: 3.3.3.7/5) cannot be uniform.

Also, star antiprism compounds with regular star $p / q$ -gon bases can be constructed if $p$ and $q$ have common factors. Example: a star 10/4-antiprism is the compound of two star 5/2-antiprisms.

Star $p / q$ -antiprisms by symmetry, for $p \leq 12$
Symmetry group	Uniform stars			Right stars
$D 4d [2 +,8] (2*4)$				3.3/2.3.4 Crossed square antiprism
$D 5h [2,5] (*225)$	3.3.3.5/2 Pentagrammic antiprism			3.3/2.3.5 crossed pentagonal antiprism
$D 5d [2 +,10] (2*5)$	3.3.3.5/3 Pentagrammic crossed-antiprism
$D 6d [2 +,12] (2*6)$				3.3/2.3.6 crossed hexagonal antiprism
$D 7h [2,7] (*227)$	3.3.3.7/2	3.3.3.7/4
$D 7d [2 +,14] (2*7)$	3.3.3.7/3
$D 8d [2 +,16] (2*8)$	3.3.3.8/3 Octagrammic antiprism	3.3.3.8/5 Octagrammic crossed-antiprism
$D 9h [2,9] (*229)$	3.3.3.9/2 Enneagrammic antiprism (9/2)	3.3.3.9/4 Enneagrammic antiprism (9/4)
$D 9d [2 +,18] (2*9)$	3.3.3.9/5 Enneagrammic crossed-antiprism
$D 10d [2 +,20] (2*10)$	3.3.3.10/3 Decagrammic antiprism
$D 11h [2,11] (*2.2.11)$	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
$D 11d [2 +,22] (2*11)$	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
$D 12d [2 +,24] (2*12)$	3.3.3.12/5	3.3.3.12/7
...	...

Related Research Articles

In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. There are only five such polyhedra:

In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.

<span class="mw-page-title-main">Equilateral triangle</span> Shape with three equal sides

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.

In geometry, a prism is a polyhedron comprising an $n$ -sided polygon base, a second base which is a translated copy of the first, and $n$ other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.

In geometry, an octagon is an eight-sided polygon or 8-gon.

In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.

In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

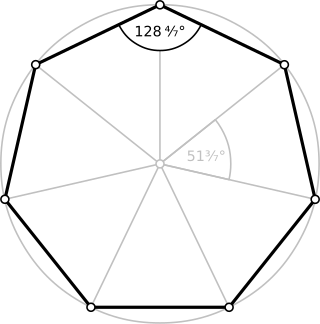
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.

In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.

In mathematics, a Catalan solid, or Archimedean dual, is a polyhedron that is dual to an Archimedean solid. There are 13 Catalan solids. They are named after the Belgian mathematician Eugène Catalan, who first described them in 1865.

In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral and the rectangles are squares, while the base and its opposite face are regular polygons, the triangular, square, and pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively.

In geometry, the area enclosed by a circle of radius $r$ is $π r 2$ . Here the Greek letter $π$ represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

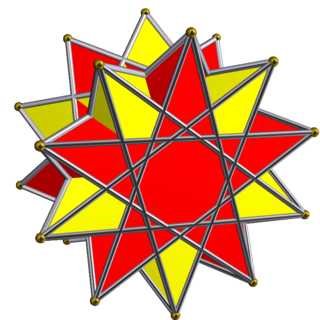
In geometry, a prismatic compound of antiprism is a category of uniform polyhedron compound. Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.

In geometry of 4 dimensions or higher, a double pyramid, duopyramid, or fusil is a polytope constructed by 2 orthogonal polytopes with edges connecting all pairs of vertices between the two. The term fusil is used by Norman Johnson as a rhombic-shape. The term duopyramid was used by George Olshevsky, as the dual of a duoprism.

In four-dimensional geometry, the spherinder, or spherical cylinder or spherical prism, is a geometric object, defined as the Cartesian product of a 3-ball of radius r₁ and a line segment of length 2r₂:

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged within each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named after mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot, Schwarz's polyhedron, or the Chinese lantern.

References

↑ Kepler, Johannes (1619). "Book II, Definition X". Harmonices Mundi (in Latin). p. 49. See also illustration A, of a heptagonal antiprism.
↑ Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (July 2008). "New light on the rediscovery of the Archimedean solids during the Renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. JSTOR 41134285.
↑ Heinze, Karl (1886). Lucke, Franz (ed.). Genetische Stereometrie (in German). B. G. Teubner. p. 14.
↑ Smyth, Piazzi (1881). "XVII. On the Constitution of the Lines forming the Low-Temperature Spectrum of Oxygen". Transactions of the Royal Society of Edinburgh. 30 (1): 419–425. doi:10.1017/s0080456800029112.
↑ Coxeter, H. S. M. (January 1928). "The pure Archimedean polytopes in six and seven dimensions". Mathematical Proceedings of the Cambridge Philosophical Society. 24 (1): 1–9. doi:10.1017/s0305004100011786.
↑ Grünbaum, Branko (2005). "Are prisms and antiprisms really boring? (Part 3)" (PDF). Geombinatorics. 15 (2): 69–78. MR 2298896.
↑ Dobbins, Michael Gene (2017). "Antiprismlessness, or: reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes". Discrete & Computational Geometry . 57 (4): 966–984. doi:10.1007/s00454-017-9874-y. MR 3639611.

External links

Media related to Antiprisms at Wikimedia Commons
Weisstein, Eric W. "Antiprism". MathWorld .
Nonconvex Prisms and Antiprisms
Paper models of prisms and antiprisms

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Kepler, Johannes (1619). "Book II, Definition X". Harmonices Mundi (in Latin). p. 49. See also illustration A, of a heptagonal antiprism.

[2] Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (July 2008). "New light on the rediscovery of the Archimedean solids during the Renaissance". Archive for History of Exact Sciences. 62 (4): 457–467. JSTOR 41134285.

[3] Heinze, Karl (1886). Lucke, Franz (ed.). Genetische Stereometrie (in German). B. G. Teubner. p. 14.

[4] Smyth, Piazzi (1881). "XVII. On the Constitution of the Lines forming the Low-Temperature Spectrum of Oxygen". Transactions of the Royal Society of Edinburgh. 30 (1): 419–425. doi:10.1017/s0080456800029112.

[5] Coxeter, H. S. M. (January 1928). "The pure Archimedean polytopes in six and seven dimensions". Mathematical Proceedings of the Cambridge Philosophical Society. 24 (1): 1–9. doi:10.1017/s0305004100011786.

[6] Grünbaum, Branko (2005). "Are prisms and antiprisms really boring? (Part 3)" (PDF). Geombinatorics. 15 (2): 69–78. MR 2298896.

[7] Dobbins, Michael Gene (2017). "Antiprismlessness, or: reducing combinatorial equivalence to projective equivalence in realizability problems for polytopes". Discrete & Computational Geometry . 57 (4): 966–984. doi:10.1007/s00454-017-9874-y. MR 3639611.

[1]

[2]

[3]

[4]

[5]

[6]

[7]