Related Research Articles
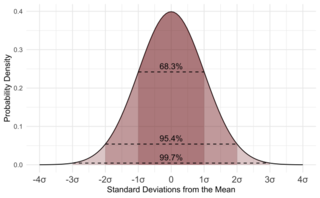
Statistics is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.

Epidemiology is the study and analysis of the distribution, patterns and determinants of health and disease conditions in a defined population.
Statistical bias is a systematic tendency which causes differences between results and facts. The bias exists in numbers of the process of data analysis, including the source of the data, the estimator chosen, and the ways the data was analyzed. Bias may have a serious impact on results, for example, to investigate people's buying habits. If the sample size is not large enough, the results may not be representative of the buying habits of all the people. That is, there may be discrepancies between the survey results and the actual results. Therefore, understanding the source of statistical bias can help to assess whether the observed results are close to the real results.
Selection bias is the bias introduced by the selection of individuals, groups, or data for analysis in such a way that proper randomization is not achieved, thereby failing to ensure that the sample obtained is representative of the population intended to be analyzed. It is sometimes referred to as the selection effect. The phrase "selection bias" most often refers to the distortion of a statistical analysis, resulting from the method of collecting samples. If the selection bias is not taken into account, then some conclusions of the study may be false.

Dependent and independent variables are variables in mathematical modeling, statistical modeling and experimental sciences. Dependent variables receive this name because, in an experiment, their values are studied under the supposition or demand that they depend, by some law or rule, on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest to predict future values.
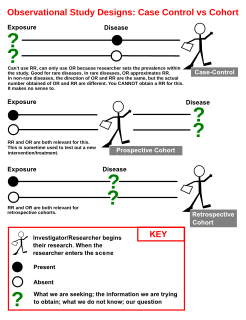
A case–control study is a type of observational study in which two existing groups differing in outcome are identified and compared on the basis of some supposed causal attribute. Case–control studies are often used to identify factors that may contribute to a medical condition by comparing subjects who have that condition/disease with patients who do not have the condition/disease but are otherwise similar. They require fewer resources but provide less evidence for causal inference than a randomized controlled trial. A case–control study produces only an odds ratio, which is an inferior measure of strength of association compared to relative risk.
In epidemiological research, recall bias is a systematic error caused by differences in the accuracy or completeness of the recollections retrieved ("recalled") by study participants regarding events or experiences from the past. It is sometimes also referred to as response bias, responder bias or reporting bias.

Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero, caused by errors in the independent variable.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.

The relative risk (RR) or risk ratio is the ratio of the probability of an outcome in an exposed group to the probability of an outcome in an unexposed group. Together with risk difference and odds ratio, relative risk measures the association between the exposure and the outcome.
A nested case–control (NCC) study is a variation of a case–control study in which cases and controls are drawn from the population in a fully enumerated cohort.

In statistics, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations. The existence of confounders is an important quantitative explanation why correlation does not imply causation.

In epidemiology, Mendelian randomization is a method using measured variation in genes to interrogate the causal effect of an exposure on an outcome. Under key assumptions, the design reduces both reverse causation and confounding, which often substantially impede or mislead the interpretation of results from epidemiological studies.
In the statistical analysis of observational data, propensity score matching (PSM) is a statistical matching technique that attempts to estimate the effect of a treatment, policy, or other intervention by accounting for the covariates that predict receiving the treatment. PSM attempts to reduce the bias due to confounding variables that could be found in an estimate of the treatment effect obtained from simply comparing outcomes among units that received the treatment versus those that did not. Paul R. Rosenbaum and Donald Rubin introduced the technique in 1983.

Nutritional epidemiology examines dietary and nutritional factors in relation to disease occurrence at a population level. Nutritional epidemiology is a relatively new field of medical research that studies the relationship between nutrition and health. It is a young discipline in epidemiology that is continuing to grow in relevance to present-day health concerns. Diet and physical activity are difficult to measure accurately, which may partly explain why nutrition has received less attention than other risk factors for disease in epidemiology. Nutritional epidemiology uses knowledge from nutritional science to aid in the understanding of human nutrition and the explanation of basic underlying mechanisms. Nutritional science information is also used in the development of nutritional epidemiological studies and interventions including clinical, case-control and cohort studies. Nutritional epidemiological methods have been developed to study the relationship between diet and disease. Findings from these studies impact public health as they guide the development of dietary recommendations including those tailored specifically for the prevention of certain diseases, conditions and cancers. It is argued by western researchers that nutritional epidemiology should be a core component in the training of all health and social service professions because of its increasing relevance and past successes in improving the health of the public worldwide. However, it is also argued that nutritional epidemiological studies yield unreliable findings as they rely on the role of diet in health and disease, which is known as an exposure that is susceptible to considerable measurement error.
A job-exposure matrix (JEM) is a tool used to assess exposure to potential health hazards in occupational epidemiological studies.
The discipline of forensic epidemiology (FE) is a hybrid of principles and practices common to both forensic medicine and epidemiology. FE is directed at filling the gap between clinical judgment and epidemiologic data for determinations of causality in civil lawsuits and criminal prosecution and defense.
Elizabeth Anne (Lianne) Sheppard is an American statistician. She specializes in biostatistics and environmental statistics, and in particular in the effects of air quality on health. She is a Professor of Environmental and Occupational Health Sciences and a Professor of Biostatistics in the University of Washington School of Public Health. In 2021, Dr. Sheppard was named to the Rohm & Haas Endowed Professorship of Public Health Sciences.
Donna Spiegelman is a biostatistician and epidemiologist who works at the interface between the two fields as a methodologist, applying statistical solutions to address potential biases in epidemiologic studies.
References
- ↑ Rothman, K.; Greenland, S.; Lash, T. (2008). Modern Epidemiology (Third ed.). Philadelphia: Lippincott Williams & Wilkins. p. 137. ISBN 978-0-7817-5564-1.
- 1 2 3 Porta, M., ed. (2008). A Dictionary of Epidemiology (Fifth ed.). New York: Oxford University Press. p. 128. ISBN 978-0-19-531449-6.
- ↑ Jurek, A. M.; Greenland, S.; Maldonado, G.; Church, T. R. (2004). "Proper interpretation of non-differential misclassification effects: Expectations vs observations". International Journal of Epidemiology. 34 (3): 680–687. doi: 10.1093/ije/dyi060 . PMID 15802377.
- ↑ Copeland, K. T.; Checkoway, H.; McMichael, A. J.; Holbrook, R. H. (1977). "Bias due to misclassification in the estimation of relative risk". American Journal of Epidemiology . 105 (5): 488–495. PMID 871121.
- ↑ Greenland, S. (1988). "Variance estimation for epidemiologic effect estimates under misclassification". Statistics in Medicine. 7 (7): 745–757. doi:10.1002/sim.4780070704. PMID 3043623.