
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.
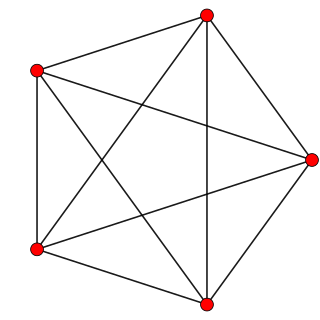
In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.

The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway called this honeycomb a cubille.

The tetrahedral-octahedral honeycomb, alternated cubic honeycomb is a quasiregular space-filling tessellation in Euclidean 3-space. It is composed of alternating regular octahedra and tetrahedra in a ratio of 1:2.

In hyperbolic geometry, the order-5 cubic honeycomb is one of four compact regular space-filling tessellations in hyperbolic 3-space. With Schläfli symbol {4,3,5}, it has five cubes {4,3} around each edge, and 20 cubes around each vertex. It is dual with the order-4 dodecahedral honeycomb.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.

In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.
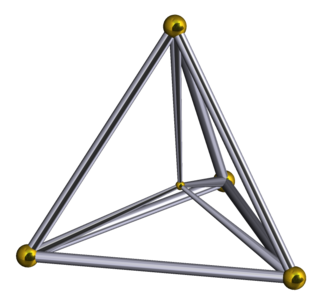
In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.
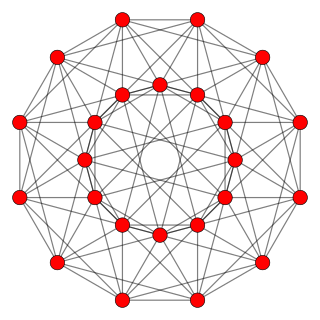
In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In the field of hyperbolic geometry, the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity.

In the field of hyperbolic geometry, the order-4 hexagonal tiling honeycomb arises as one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.

The order-6 cubic honeycomb is a paracompact regular space-filling tessellation in hyperbolic 3-space. It is paracompact because it has vertex figures composed of an infinite number of facets, with all vertices as ideal points at infinity. With Schläfli symbol {4,3,6}, the honeycomb has six ideal cubes meeting along each edge. Its vertex figure is an infinite triangular tiling. Its dual is the order-4 hexagonal tiling honeycomb.

In the geometry of hyperbolic 3-space, the square tiling honeycomb is one of 11 paracompact regular honeycombs. It is called paracompact because it has infinite cells, whose vertices exist on horospheres and converge to a single ideal point at infinity. Given by Schläfli symbol {4,4,3}, it has three square tilings, {4,4}, around each edge, and six square tilings around each vertex, in a cubic {4,3} vertex figure.

The order-4 octahedral honeycomb is a regular paracompact honeycomb in hyperbolic 3-space. It is paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {3,4,4}, it has four ideal octahedra around each edge, and infinite octahedra around each vertex in a square tiling vertex figure.




































































































