Racks and quandles

In mathematics, racks and quandles are sets with binary operations satisfying axioms analogous to the Reidemeister moves used to manipulate knot diagrams.

Contents

• History
• Racks
• Quandles
• Examples and applications
• See also
• References
• External links

While mainly used to obtain invariants of knots, they can be viewed as algebraic constructions in their own right. In particular, the definition of a quandle axiomatizes the properties of conjugation in a group.

History

In 1942, Mituhisa Takasaki  [ ja ] introduced an algebraic structure which he called a kei ( 圭 ), ^{[1] [2]} which would later come to be known as an involutive quandle. ^[3] His motivation was to find a nonassociative algebraic structure to capture the notion of a reflection in the context of finite geometry. ^{[2] [3]} The idea was rediscovered and generalized in an unpublished 1959 correspondence between John Conway and Gavin Wraith, who at the time were undergraduate students at the University of Cambridge. It is here that the modern definitions of quandles and of racks first appear. Wraith had become interested in these structures (which he initially dubbed sequentials) while at school. ^[4] Conway renamed them wracks, partly as a pun on his colleague's name, and partly because they arise as the remnants (or 'wrack and ruin') of a group when one discards the multiplicative structure and considers only the conjugation structure. The spelling 'rack' has now become prevalent.

These constructs surfaced again in the 1980s: in a 1982 paper by David Joyce ^[5] (where the term quandle, an arbitrary nonsense word, was coined), ^[6] in a 1982 paper by Sergei Matveev (under the name distributive groupoids ) ^[7] and in a 1986 conference paper by Egbert Brieskorn (where they were called automorphic sets ). ^[8] A detailed overview of racks and their applications in knot theory may be found in the paper by Colin Rourke and Roger Fenn. ^[9]

Racks

A rack may be defined as a set ${\displaystyle \mathrm {R} }$ with a binary operation ${\displaystyle \triangleleft }$ such that for every ${\displaystyle a,b,c\in \mathrm {R} }$ the self-distributive law holds:

${\displaystyle a\triangleleft (b\triangleleft c)=(a\triangleleft b)\triangleleft (a\triangleleft c)}$

and for every ${\displaystyle a,b\in \mathrm {R} ,}$ there exists a unique ${\displaystyle c\in \mathrm {R} }$ such that

${\displaystyle a\triangleleft c=b.}$

This definition, while terse and commonly used, is suboptimal for certain purposes because it contains an existential quantifier which is not really necessary. To avoid this, we may write the unique ${\displaystyle c\in \mathrm {R} }$ such that ${\displaystyle a\triangleleft c=b}$ as ${\displaystyle b\triangleright a.}$ We then have

${\displaystyle a\triangleleft c=b\iff c=b\triangleright a,}$

and thus

${\displaystyle a\triangleleft (b\triangleright a)=b,}$

and

${\displaystyle (a\triangleleft b)\triangleright a=b.}$

Using this idea, a rack may be equivalently defined as a set ${\displaystyle \mathrm {R} }$ with two binary operations ${\displaystyle \triangleleft }$ and ${\displaystyle \triangleright }$ such that for all ${\displaystyle a,b,c\in \mathrm {R} {\text{:}}}$

1. ${\displaystyle a\triangleleft (b\triangleleft c)=(a\triangleleft b)\triangleleft (a\triangleleft c)}$ (left self-distributive law)
2. ${\displaystyle (c\triangleright b)\triangleright a=(c\triangleright a)\triangleright (b\triangleright a)}$ (right self-distributive law)
3. ${\displaystyle (a\triangleleft b)\triangleright a=b}$
4. ${\displaystyle a\triangleleft (b\triangleright a)=b}$

It is convenient to say that the element ${\displaystyle a\in \mathrm {R} }$ is acting from the left in the expression ${\displaystyle a\triangleleft b,}$ and acting from the right in the expression ${\displaystyle b\triangleright a.}$ The third and fourth rack axioms then say that these left and right actions are inverses of each other. Using this, we can eliminate either one of these actions from the definition of rack. If we eliminate the right action and keep the left one, we obtain the terse definition given initially.

Many different conventions are used in the literature on racks and quandles. For example, many authors prefer to work with just the right action. Furthermore, the use of the symbols ${\displaystyle \triangleleft }$ and ${\displaystyle \triangleright }$ is by no means universal: many authors use exponential notation

${\displaystyle a\triangleleft b={}^{a}b}$

and

${\displaystyle b\triangleright a=b^{a},}$

while many others write

${\displaystyle b\triangleright a=b\star a.}$

Yet another equivalent definition of a rack is that it is a set where each element acts on the left and right as automorphisms of the rack, with the left action being the inverse of the right one. In this definition, the fact that each element acts as automorphisms encodes the left and right self-distributivity laws, and also these laws:

${\displaystyle {\begin{aligned}a\triangleleft (b\triangleright c)&=(a\triangleleft b)\triangleright (a\ \triangleleft c)\\(c\triangleleft b)\triangleright a&=(c\triangleright a)\triangleleft (b\triangleright a)\end{aligned}}}$

which are consequences of the definition(s) given earlier.

Quandles

A quandle is defined as an idempotent rack, ${\displaystyle \mathrm {Q} ,}$ such that for all ${\displaystyle a\in \mathrm {Q} }$

${\displaystyle a\triangleleft a=a,}$

or equivalently

${\displaystyle a\triangleright a=a.}$

Examples and applications

Every group gives a quandle where the operations come from conjugation:

${\displaystyle {\begin{aligned}a\triangleleft b&=aba^{-1}\\b\triangleright a&=a^{-1}ba\\&=a^{-1}\triangleleft b\end{aligned}}}$

In fact, every equational law satisfied by conjugation in a group follows from the quandle axioms. So, one can think of a quandle as what is left of a group when we forget multiplication, the identity, and inverses, and only remember the operation of conjugation.

Every tame knot in three-dimensional Euclidean space has a 'fundamental quandle'. To define this, one can note that the fundamental group of the knot complement, or knot group, has a presentation (the Wirtinger presentation) in which the relations only involve conjugation. So, this presentation can also be used as a presentation of a quandle. The fundamental quandle is a very powerful invariant of knots. In particular, if two knots have isomorphic fundamental quandles then there is a homeomorphism of three-dimensional Euclidean space, which may be orientation reversing, taking one knot to the other.

Less powerful but more easily computable invariants of knots may be obtained by counting the homomorphisms from the knot quandle to a fixed quandle ${\displaystyle \mathrm {Q} .}$ Since the Wirtinger presentation has one generator for each strand in a knot diagram, these invariants can be computed by counting ways of labelling each strand by an element of ${\displaystyle \mathrm {Q} ,}$ subject to certain constraints. More sophisticated invariants of this sort can be constructed with the help of quandle cohomology.

The Alexander quandles are also important, since they can be used to compute the Alexander polynomial of a knot. Let ${\displaystyle \mathrm {A} }$ be a module over the ring ${\displaystyle \mathbb {Z} [t,t^{-1}]}$ of Laurent polynomials in one variable. Then the Alexander quandle is ${\displaystyle \mathrm {A} }$ made into a quandle with the left action given by

${\displaystyle a\triangleleft b=tb+(1-t)a.}$

Racks are a useful generalization of quandles in topology, since while quandles can represent knots on a round linear object (such as rope or a thread), racks can represent ribbons, which may be twisted as well as knotted.

A quandle ${\displaystyle \mathrm {Q} }$ is said to be involutory if for all ${\displaystyle a,b\in \mathrm {Q} ,}$

${\displaystyle a\triangleleft (a\triangleleft b)=b}$

or equivalently,

${\displaystyle (b\triangleright a)\triangleright a=b.}$

Any symmetric space gives an involutory quandle, where ${\displaystyle a\triangleleft b}$ is the result of 'reflecting ${\displaystyle b}$ through ${\displaystyle a}$'.

See also

• Biracks and biquandles
• Laver table

Related Research Articles

In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:

In mathematics, a group is a set with an operation that associates an element of the set to every pair of elements of the set and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

In abstract algebra, a normal subgroup is a subgroup that is invariant under conjugation by members of the group of which it is a part. In other words, a subgroup of the group is normal in if and only if for all and . The usual notation for this relation is .

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. It is usually denoted with the symbol ⋉. There are two closely related concepts of semidirect product:

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. Informally, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.

In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H, or in blackboard bold by Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form

In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality is always true in elementary algebra. For example, in elementary arithmetic, one has Therefore, one would say that multiplication distributes over addition.

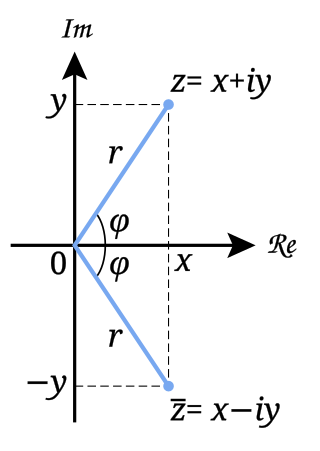
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if and are real numbers, then the complex conjugate of is The complex conjugate of is often denoted as or .

In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n × n orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact.

In mathematics, and more specifically in abstract algebra, a *-algebra is a mathematical structure consisting of two involutive ringsR and A, where R is commutative and A has the structure of an associative algebra over R. Involutive algebras generalize the idea of a number system equipped with conjugation, for example the complex numbers and complex conjugation, matrices over the complex numbers and conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints. However, it may happen that an algebra admits no involution.

In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence cannot be decomposed into a direct sum of simple modules. A composition series of a module M is a finite increasing filtration of M by submodules such that the successive quotients are simple and serves as a replacement of the direct sum decomposition of M into its simple constituents.

In mathematics, the adjoint representation of a Lie group G is a way of representing the elements of the group as linear transformations of the group's Lie algebra, considered as a vector space. For example, if G is , the Lie group of real n-by-n invertible matrices, then the adjoint representation is the group homomorphism that sends an invertible n-by-n matrix to an endomorphism of the vector space of all linear transformations of defined by: .

In abstract algebra, a semiring is an algebraic structure. Semirings are a generalization of rings, dropping the requirement that each element must have an additive inverse. At the same time, semirings are a generalization of bounded distributive lattices.

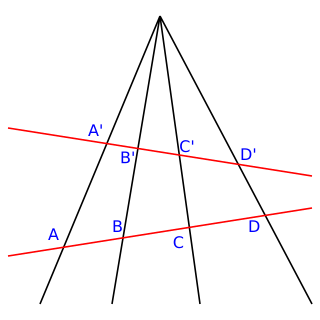
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points A, B, C, D on a line, their cross ratio is defined as

A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum and a unique infimum. An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor.

In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.

In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an -dimensional manifold, or -manifold for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of -dimensional Euclidean space.

The name paravector is used for the combination of a scalar and a vector in any Clifford algebra, known as geometric algebra among physicists.

In physics, the Majorana equation is a relativistic wave equation. It is named after the Italian physicist Ettore Majorana, who proposed it in 1937 as a means of describing fermions that are their own antiparticle. Particles corresponding to this equation are termed Majorana particles, although that term now has a more expansive meaning, referring to any fermionic particle that is its own anti-particle.

References

External links

• Knot Quandaries Quelled by Quandles - An undergraduate introduction to quandles and another knot invariants
• A Survey of Quandle Ideas by Scott Carter
• Knot Invariants Derived from Quandles and Racks by Seiichi Kamada
• Shelves, Racks, Spindles and Quandles, p. 56 of Lie 2-Algebras by Alissa Crans
• https://ncatlab.org/nlab/show/quandle