Plume (fluid dynamics)

Last updated
Controlled burn of oil creating a smoke plume Defense.gov photo essay 100506-N-6070S-346.jpg
Controlled burn of oil creating a smoke plume

In hydrodynamics, a plume or a column is a vertical body of one fluid moving through another. Several effects control the motion of the fluid, including momentum (inertia), diffusion and buoyancy (density differences). Pure jets and pure plumes define flows that are driven entirely by momentum and buoyancy effects, respectively. Flows between these two limits are usually described as forced plumes or buoyant jets. "Buoyancy is defined as being positive" when, in the absence of other forces or initial motion, the entering fluid would tend to rise. Situations where the density of the plume fluid is greater than its surroundings (i.e. in still conditions, its natural tendency would be to sink), but the flow has sufficient initial momentum to carry it some distance vertically, are described as being negatively buoyant. [1]

Contents

Movement

Usually, as a plume moves away from its source, it widens because of entrainment of the surrounding fluid at its edges. Plume shapes can be influenced by flow in the ambient fluid (for example, if local wind blowing in the same direction as the plume results in a co-flowing jet). This usually causes a plume which has initially been 'buoyancy-dominated' to become 'momentum-dominated' (this transition is usually predicted by a dimensionless number called the Richardson number).

Flow and detection

A further phenomenon of importance is whether a plume has laminar flow or turbulent flow. Usually, there is a transition from laminar to turbulent as the plume moves away from its source. This phenomenon can be clearly seen in the rising column of smoke from a cigarette. When high accuracy is required, computational fluid dynamics (CFD) can be employed to simulate plumes, but the results can be sensitive to the turbulence model chosen. CFD is often undertaken for rocket plumes, where condensed phase constituents can be present in addition to gaseous constituents. These types of simulations can become quite complex, including afterburning and thermal radiation, and (for example) ballistic missile launches are often detected by sensing hot rocket plumes.

Spacecraft designers are sometimes concerned with impingement of attitude control system thruster plumes onto sensitive subsystems like solar arrays and star trackers, or with the impingement of rocket engine plumes onto moon or planetary surfaces where they can cause local damage or even mid-term disturbances to planetary atmospheres.

Another phenomenon which can also be seen clearly in the flow of smoke from a cigarette is that the leading-edge of the flow, or the starting-plume, is quite often approximately in the shape of a ring-vortex (smoke ring). [2]

Types

Pollutants released to the ground can work their way down into the groundwater, leading to groundwater pollution. The resulting body of polluted water within an aquifer is called a plume, with its migrating edges called plume fronts. Plumes are used to locate, map, and measure water pollution within the aquifer's total body of water, and plume fronts to determine directions and speed of the contamination's spreading in it. [3]

Plumes are of considerable importance in the atmospheric dispersion modelling of air pollution. A classic work on the subject of air pollution plumes is that by Gary Briggs. [4] [5]

A thermal plume is one which is generated by gas rising above a heat source. The gas rises because thermal expansion makes warm gas less dense than the surrounding cooler gas.

Simple plume modeling

Simple modelling will enable many properties of fully developed, turbulent plumes to be investigated. [6] Many of the classic scaling arguments were developed in a combined analytic and laboratory study described in an influential paper by Bruce Morton, G.I. Taylor and Stewart Turner [7] and this and subsequent work is described in the popular monograph of Stewart Turner. [8]

  1. It is usually sufficient to assume that the pressure gradient is set by the gradient far from the plume (this approximation is similar to the usual Boussinesq approximation).
  2. The distribution of density and velocity across the plume are modelled either with simple Gaussian distributions or else are taken as uniform across the plume (the so-called 'top hat' model).
  3. The rate of entrainment into the plume is proportional to the local velocity. [7] Though initially thought to be a constant, recent work has shown that the entrainment coefficient varies with the local Richardson number. [9] Typical values for the entrainment coefficient are of about 0.08 for vertical jets and 0.12 for vertical, buoyant plumes while for bent-over plumes, the entrainment coefficient is about 0.6.
  4. Conservation equations for mass (including entrainment), and momentum and buoyancy fluxes are sufficient for a complete description of the flow in many cases. [7] [10] For a simple rising plume these equations predict that the plume will widen at a constant half-angle of about 6 to 15 degrees.

The value of the entrainment coefficient is the key parameter in simple plume models. Research continues into assessing how the entrainment coefficient is affected by, for example, the geometry of a plume, [11] suspended particles within a plume, [12] and background rotation. [13]

Gaussian plume modelling

Gaussian plume models can be used in several fluid dynamics scenarios to calculate concentration distribution of solutes, such as a smoke stack release or contaminant released in a river. Gaussian distributions are established by Fickian diffusion, and follow a Gaussian (bell-shaped) distribution. [14] For calculating the expected concentration of a one dimensional instantaneous point source we consider a mass released at an instantaneous point in time, in a one dimensional domain along . This will give the following equation: [15]

where is the mass released at time and location , and is the diffusivity . This equation makes the following four assumptions: [16]

  1. The mass is released instantaneously.
  2. The mass is released in an infinite domain.
  3. The mass spreads only through diffusion.
  4. Diffusion does not vary in space. [14]

See also

Related Research Articles

In fluid mechanics, the Rayleigh number (Ra, after Lord Rayleigh) for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free (or natural) convection. It characterises the fluid's flow regime: a value in a certain lower range denotes laminar flow; a value in a higher range, turbulent flow. Below a certain critical value, there is no fluid motion and heat transfer is by conduction rather than convection. For most engineering purposes, the Rayleigh number is large, somewhere around 106 to 108.

In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between those layers.

<span class="mw-page-title-main">Mixing (process engineering)</span> Process of mechanically stirring a heterogeneous mixture to homogenize it

In industrial process engineering, mixing is a unit operation that involves manipulation of a heterogeneous physical system with the intent to make it more homogeneous. Familiar examples include pumping of the water in a swimming pool to homogenize the water temperature, and the stirring of pancake batter to eliminate lumps (deagglomeration).

In fluid dynamics, the Schmidt number of a fluid is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and it is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes. It was named after German engineer Ernst Heinrich Wilhelm Schmidt (1892–1975).

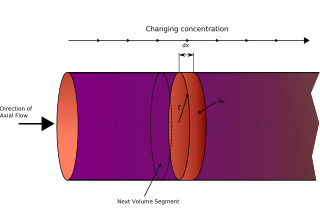
<span class="mw-page-title-main">Plug flow reactor model</span> Reactor simulation model

The plug flow reactor model is a model used to describe chemical reactions in continuous, flowing systems of cylindrical geometry. The PFR model is used to predict the behavior of chemical reactors of such design, so that key reactor variables, such as the dimensions of the reactor, can be estimated.

Entrainment is the transport of fluid across an interface between two bodies of fluid by a shear-induced turbulent flux. Entrainment is important in turbulent jets, plumes, and gravity currents, and is an ongoing topic of research.

<span class="mw-page-title-main">Atmospheric dispersion modeling</span> Mathematical simulation of how air pollutants disperse in the ambient atmosphere

Atmospheric dispersion modeling is the mathematical simulation of how air pollutants disperse in the ambient atmosphere. It is performed with computer programs that include algorithms to solve the mathematical equations that govern the pollutant dispersion. The dispersion models are used to estimate the downwind ambient concentration of air pollutants or toxins emitted from sources such as industrial plants, vehicular traffic or accidental chemical releases. They can also be used to predict future concentrations under specific scenarios. Therefore, they are the dominant type of model used in air quality policy making. They are most useful for pollutants that are dispersed over large distances and that may react in the atmosphere. For pollutants that have a very high spatio-temporal variability and for epidemiological studies statistical land-use regression models are also used.

The National Atmospheric Release Advisory Center (NARAC) is located at the University of California's Lawrence Livermore National Laboratory. It is a national support and resource center for planning, real-time assessment, emergency response, and detailed studies of incidents involving a wide variety of hazards, including nuclear, radiological, chemical, biological, and natural emissions.

The following outline is provided as an overview of and topical guide to air pollution dispersion: In environmental science, air pollution dispersion is the distribution of air pollution into the atmosphere. Air pollution is the introduction of particulates, biological molecules, or other harmful materials into Earth's atmosphere, causing disease, death to humans, damage to other living organisms such as food crops, and the natural or built environment. Air pollution may come from anthropogenic or natural sources. Dispersion refers to what happens to the pollution during and after its introduction; understanding this may help in identifying and controlling it.

MERCURE is an atmospheric dispersion modeling CFD code developed by Électricité de France (EDF) and distributed by ARIA Technologies, a French company.

<span class="mw-page-title-main">Eddy diffusion</span> Mixing of fluids due to eddy currents

In fluid dynamics, eddy diffusion, eddy dispersion, or turbulent diffusion is a process by which fluid substances mix together due to eddy motion. These eddies can vary widely in size, from subtropical ocean gyres down to the small Kolmogorov microscales, and occur as a result of turbulence. The theory of eddy diffusion was first developed by Sir Geoffrey Ingram Taylor.

<span class="mw-page-title-main">Diffusion</span> Transport of dissolved species from the highest to the lowest concentration region

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing.

Turbulent diffusion is the transport of mass, heat, or momentum within a system due to random and chaotic time dependent motions. It occurs when turbulent fluid systems reach critical conditions in response to shear flow, which results from a combination of steep concentration gradients, density gradients, and high velocities. It occurs much more rapidly than molecular diffusion and is therefore extremely important for problems concerning mixing and transport in systems dealing with combustion, contaminants, dissolved oxygen, and solutions in industry. In these fields, turbulent diffusion acts as an excellent process for quickly reducing the concentrations of a species in a fluid or environment, in cases where this is needed for rapid mixing during processing, or rapid pollutant or contaminant reduction for safety.

In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.

<span class="mw-page-title-main">Stewart Turner</span> Australian geophysicist (1930–2022)

John Stewart Turner, FAA, FRS was an Australian geophysicist.

<span class="mw-page-title-main">Bubble column reactor</span>

A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor, fluidized bed reactor, and bubble column reactor. A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.

Particle-laden flows refers to a class of two-phase fluid flow, in which one of the phases is continuously connected and the other phase is made up of small, immiscible, and typically dilute particles. Fine aerosol particles in air is an example of a particle-laden flow; the aerosols are the dispersed phase, and the air is the carrier phase.

Schneider flow describes the axisymmetric outer flow induced by a laminar or turbulent jet having a large jet Reynolds number or by a laminar plume with a large Grashof number, in the case where the fluid domain is bounded by a wall. When the jet Reynolds number or the plume Grashof number is large, the full flow field constitutes two regions of different extent: a thin boundary-layer flow that may identified as the jet or as the plume and a slowly moving fluid in the large outer region encompassing the jet or the plume. The Schneider flow describing the latter motion is an exact solution of the Navier-Stokes equations, discovered by Wilhelm Schneider in 1981. The solution was discovered also by A. A. Golubinskii and V. V. Sychev in 1979, however, was never applied to flows entrained by jets. The solution is an extension of Taylor's potential flow solution to arbitrary Reynolds number.

<span class="mw-page-title-main">High pressure jet</span>

A high pressure jet is a stream of pressurized fluid that is released from an environment at a significantly higher pressure than ambient pressure from a nozzle or orifice, due to operational or accidental release. In the field of safety engineering, the release of toxic and flammable gases has been the subject of many R&D studies because of the major risk that they pose to the health and safety of workers, equipment and environment. Intentional or accidental release may occur in an industrial settings like natural gas processing plants, oil refineries and hydrogen storage facilities.

References

  1. ↑ Turner, J.S. (1979), "Buoyancy effects in fluids", Ch.6, pp.165--&, Cambridge University Press
  2. ↑ Turner, J. S. (1962). The Starting Plume in Neutral Surroundings, J. Fluid Mech. vol 13, pp356-368
  3. ↑ Fetter, C.W. Jr 1998 Contaminant Hydrogeology
  4. ↑ Briggs, Gary A. (1975). Plume Rise Predictions, Chapter 3 in Lectures on Air Pollution and Environmental Impact Analysis, Duanne A. Haugen, editor, Amer. Met. Soc.
  5. ↑ Beychok, Milton R. (2005). Fundamentals Of Stack Gas Dispersion (4th ed.). author-published. ISBN   0-9644588-0-2.
  6. ↑ Scase, M. M., Caulfield, C. P., Dalziel, S. B. & Hunt, J. C. R. (2006). Time-dependent plumes and jets with decreasing source strengths, J. Fluid Mech. vol 563, pp443-461
  7. 1 2 3 Morton, B. R., Turner, J. S., and Taylor, G.I. (1956), Turbulent gravitational convection from maintained and instantaneous sources, P. Roy. Soc. Lond., vol. 234, pp.1--&
  8. ↑ Turner, J. S.; Turner, John Stewart (1979-12-20). Buoyancy Effects in Fluids. Cambridge University Press. ISBN   978-0-521-29726-4.
  9. ↑ Kaminski, E. Tait, S. and Carazzo, G. (2005), Turbulent entrainment in jets with arbitrary buoyancy, J. Fluid Mech., vol. 526, pp.361--376
  10. ↑ Woods, A.W. (2010), Turbulent plumes in nature, Annu. Rev. Fluid Mech., Vol. 42, pp. 391--412
  11. ↑ Richardson, James; Hunt, Gary R. (10 March 2022). "What is the entrainment coefficient of a pure turbulent line plume?". Journal of Fluid Mechanics. 934. Bibcode:2022JFM...934A..11R. doi: 10.1017/jfm.2021.1070 . S2CID   245908780.
  12. ↑ McConnochie, Craig D.; Cenedese, Claudia; McElwaine, Jim N. (23 December 2021). "Entrainment into particle-laden turbulent plumes". Physical Review Fluids. 6 (12): 123502. arXiv: 2109.01240 . Bibcode:2021PhRvF...6l3502M. doi:10.1103/PhysRevFluids.6.123502. S2CID   237416756.
  13. ↑ Fabregat Tomàs, Alexandre; Poje, Andrew C.; Özgökmen, Tamay M.; Dewar, William K. (August 2016). "Effects of rotation on turbulent buoyant plumes in stratified environments". Journal of Geophysical Research: Oceans. 121 (8): 5397–5417. Bibcode:2016JGRC..121.5397F. doi: 10.1002/2016JC011737 .
  14. 1 2 Connolly, Paul. "Gaussian Plume Model". personalpages.manchester.ac.uk. Retrieved 25 April 2017.
  15. ↑ Heidi Nepf. 1.061 Transport Processes in the Environment. Fall 2008. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu/ License: Creative Commons BY-NC-SA.
  16. ↑ Variano, Evan. Mass Transport in Environmental Flows. UC Berkeley.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.