This article includes a list of general references, but it lacks sufficient corresponding inline citations .(April 2010) |
Differential phase is a kind of linearity distortion which affects the color hue in TV broadcasting.
This article includes a list of general references, but it lacks sufficient corresponding inline citations .(April 2010) |
Differential phase is a kind of linearity distortion which affects the color hue in TV broadcasting.
Composite color video signal (CCVS) consists of three terms:
The first two terms are usually called composite video signal (CVS)
The modulation technique of the color subcarrier is quadrature amplitude modulation (QAM) both in PAL and NTSC systems. The amplitude of the color signal represents the saturation of the color and the phase lag of the color signal with respect to a certain reference which is called colorburst represents the hue; i.e., each phase lag is assigned for a different color hue. So, in order to reproduce the original color in the receiver, the phase difference between the colorburst and the color signal must be kept constant throughout the broadcasting.
The colorburst is a 10 period signal of color carrier (3.58 MHz in System M and 4.43 MHz in System B and System G). It is superimposed on the back porch of the CVS. The peak to peak amplitude is about 300 mV. That means that, when the color signal has a low luminance, its DC component is comparable to that of the colorburst. All dark colors have more or less the same DC component as the colorburst. But light colors have a higher luminance and hence a higher DC component.
During broadcasting, the inherent non linearity in electronic devices may cause a level dependent phase shift. [1] Differential phase distortion (DP or dP) is the shift of color signal phase with respect to the colorburst phase. When DC (brightness / luminance) levels of light colors and the colorburst are different, the hue of the light colors may change. Especially a slight change in skin color may be irritating to viewers (too yellow or too red skin color depending on whether shift is positive or negative).
To solve the problem of differential phase distortion in PAL system, the polarity of both the colorburst and the color signal are reversed in each consecutive lines. [2] [3] So in odd lines the phase of the colorburst leads and in the even lines the phase of the color signal leads. However, if there is DP distortion in the system, the shift caused by DP has always the same polarity, thus the overall shift is more than the original in even line and less than the original in the odd line by the same amount. The average of two lines yields the original phase difference and thus the color.

The mathematics involved is as follows:
Let be the phase difference of the color signal with respect to colorburst and be the extra shift introduced by DP.
The original signal is
If there is a DP distortion, the received signal for the first line is
In the second line (after multiplying by -1)
The average is
So while the effect of diminishes on the color hue, the amplitude of the color signal is reduced by which means that color saturation is reduced.
Frequency modulation synthesis is a form of sound synthesis whereby the frequency of a waveform is changed by modulating its frequency with a modulator. The (instantaneous) frequency of an oscillator is altered in accordance with the amplitude of a modulating signal.
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force F proportional to the displacement x:
In optics, polarized light can be described using the Jones calculus, discovered by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices. When light crosses an optical element the resulting polarization of the emerging light is found by taking the product of the Jones matrix of the optical element and the Jones vector of the incident light. Note that Jones calculus is only applicable to light that is already fully polarized. Light which is randomly polarized, partially polarized, or incoherent must be treated using Mueller calculus.
Phase modulation (PM) is a modulation pattern for conditioning communication signals for transmission. It encodes a message signal as variations in the instantaneous phase of a carrier wave. Phase modulation is one of the two principal forms of angle modulation, together with frequency modulation.
Double-sideband suppressed-carrier transmission (DSB-SC) is transmission in which frequencies produced by amplitude modulation (AM) are symmetrically spaced above and below the carrier frequency and the carrier level is reduced to the lowest practical level, ideally being completely suppressed.
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation. An elliptically polarized wave may be resolved into two linearly polarized waves in phase quadrature, with their polarization planes at right angles to each other. Since the electric field can rotate clockwise or counterclockwise as it propagates, elliptically polarized waves exhibit chirality.
In signal processing, group delay and phase delay are two related ways of describing how a signal's frequency components are delayed in time when passing through a linear time-invariant (LTI) system. Phase delay describes the time shift of a sinusoidal component. Group delay describes the time shift of the envelope of a wave packet, a "pack" or "group" of oscillations centered around one frequency that travel together, formed for instance by multiplying a sine wave by an envelope.
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the change per unit length, but it is otherwise dimensionless. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.

In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit.
Rayleigh fading is a statistical model for the effect of a propagation environment on a radio signal, such as that used by wireless devices.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when plane waves are incident on a diffracting object, and the diffraction pattern is viewed at a sufficiently long distance from the object, and also when it is viewed at the focal plane of an imaging lens. In contrast, the diffraction pattern created near the diffracting object and is given by the Fresnel diffraction equation.
In mathematics and signal processing, an analytic signal is a complex-valued function that has no negative frequency components. The real and imaginary parts of an analytic signal are real-valued functions related to each other by the Hilbert transform.

In physics and engineering, a phasor is a complex number representing a sinusoidal function whose amplitude, angular frequency, and initial phase are time-invariant. It is related to a more general concept called analytic representation, which decomposes a sinusoid into the product of a complex constant and a factor depending on time and frequency. The complex constant, which depends on amplitude and phase, is known as a phasor, or complex amplitude, and sinor or even complexor.
In signal processing, linear phase is a property of a filter where the phase response of the filter is a linear function of frequency. The result is that all frequency components of the input signal are shifted in time by the same constant amount, which is referred to as the group delay. Consequently, there is no phase distortion due to the time delay of frequencies relative to one another.

In the mathematical theory of bifurcations, a Hopfbifurcation is a critical point where, as time passes, a system's stability switches and a periodic solution arises. More accurately, it is a local bifurcation in which a fixed point of a dynamical system loses stability, as a pair of complex conjugate eigenvalues—of the linearization around the fixed point—crosses the complex plane imaginary axis as a parameter crosses a threshold value. Under reasonably generic assumptions about the dynamical system, the fixed point becomes a small-amplitude limit cycle as the parameter changes.

A pendulum is a body suspended from a fixed support so that it swings freely back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.
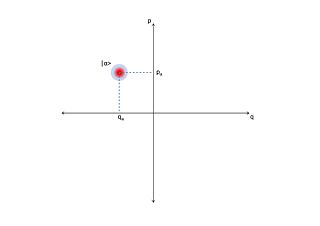
In quantum optics, an optical phase space is a phase space in which all quantum states of an optical system are described. Each point in the optical phase space corresponds to a unique state of an optical system. For any such system, a plot of the quadratures against each other, possibly as functions of time, is called a phase diagram. If the quadratures are functions of time then the optical phase diagram can show the evolution of a quantum optical system with time.
SigSpec is a statistical technique to provide the reliability of periodicities in a measured time series. It relies on the amplitude spectrum obtained by the Discrete Fourier transform (DFT) and assigns a quantity called the spectral significance to each amplitude. This quantity is a logarithmic measure of the probability that the given amplitude level would be seen in white noise, in the sense of a type I error. It represents the answer to the question, “What would be the chance to obtain an amplitude like the measured one or higher, if the analysed time series were random?”
Differential gain is a kind of linearity distortion that affects the amplification and transmission of analog signals. It can visibly affect color saturation in analog TV broadcasting.
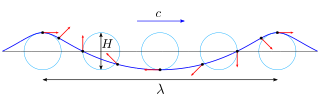
In fluid dynamics, a trochoidal wave or Gerstner wave is an exact solution of the Euler equations for periodic surface gravity waves. It describes a progressive wave of permanent form on the surface of an incompressible fluid of infinite depth. The free surface of this wave solution is an inverted (upside-down) trochoid – with sharper crests and flat troughs. This wave solution was discovered by Gerstner in 1802, and rediscovered independently by Rankine in 1863.