Axial symmetry

Nutation is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behaviour of a mechanism. In an appropriate reference frame it can be defined as a change in the second Euler angle. If it is not caused by forces external to the body, it is called free nutation or Euler nutation. A pure nutation is a movement of a rotational axis such that the first Euler angle is constant. Therefore it can be seen that the circular red arrow in the diagram indicates the combined effects of precession and nutation, while nutation in the absence of precession would only change the tilt from vertical. However, in spacecraft dynamics, precession is sometimes referred to as nutation.

Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In other words, if the axis of rotation of a body is itself rotating about a second axis, that body is said to be precessing about the second axis. A motion in which the second Euler angle changes is called nutation. In physics, there are two types of precession: torque-free and torque-induced.

Rotation or rotational motion is the circular movement of an object around a central line, known as axis of rotation. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a center of rotation. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation, in contrast to rotation around a fixed axis.

In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.

A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. For each wallpaper there corresponds a group of congruent transformations, with function composition as the group operation. Thus, a wallpaper group is a mathematical classification of a two‑dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tessellations, tiles and physical wallpaper.

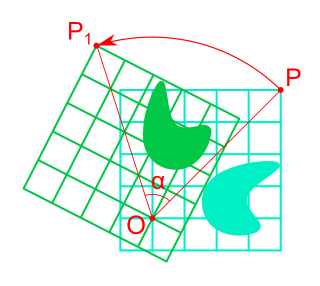
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.

Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.

In physics, symmetry breaking is a phenomenon where a disordered but symmetric state collapses into an ordered, but less symmetric state. This collapse is often one of many possible bifurcations that a particle can take as it approaches a lower energy state. Due to the many possibilities, an observer may assume the result of the collapse to be arbitrary. This phenomenon is fundamental to quantum field theory (QFT), and further, contemporary understandings of physics. Specifically, it plays a central role in the Glashow–Weinberg–Salam model which forms part of the Standard model modelling the electroweak sector.

In geometry, circular symmetry is a type of continuous symmetry for a planar object that can be rotated by any arbitrary angle and map onto itself.

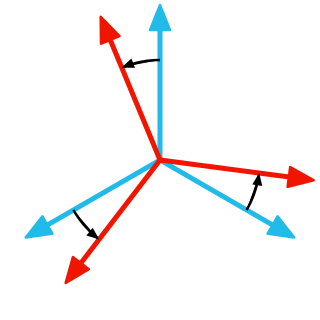
In geometry, the orientation, attitude, bearing, direction, or angular position of an object – such as a line, plane or rigid body – is part of the description of how it is placed in the space it occupies. More specifically, it refers to the imaginary rotation that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement, in which case it may be necessary to add an imaginary translation to change the object's position. The position and orientation together fully describe how the object is placed in space. The above-mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its position does not change when it rotates.

A regular octahedron has 24 rotational symmetries, and 48 symmetries altogether. These include transformations that combine a reflection and a rotation. A cube has the same set of symmetries, since it is the polyhedron that is dual to an octahedron.

Rotation around a fixed axis or axial rotation is a special case of rotational motion around an axis of rotation fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis of rotation changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible; if two rotations are forced at the same time, a new axis of rotation will result.

In geometry, a compound of four tetrahedra can be constructed by four tetrahedra in a number of different symmetry positions.

In geometry, an object has symmetry if there is an operation or transformation that maps the figure/object onto itself. Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be symmetric under rotation or to have rotational symmetry. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry.