
|

|

|

|

|

|

|

|

|

|

|

|

|
虛數是指可以寫作實數與虛數單位 乘積的複數[1]
,並定義其性質為
乘積的複數[1]
,並定義其性質為 ,以此定義,0可被視為同時是實數也是虛數(純虛數)的數值[2]。
,以此定義,0可被視為同時是實數也是虛數(純虛數)的數值[2]。
17世紀著名數學家笛卡爾所著《幾何學》(法語:La Géométrie)一書中,命名其為nombre imaginaire(虛構的數),成為了虛數(imaginary number)一詞的由來。
後來在歐拉和高斯的研究之後,發現虛數可對應平面上的縱軸,與對應平面上橫軸的實數同樣真實。虛軸和實軸構成的平面稱複數平面,複數平面上每一點對應着一個複數。
 複數平面的圖示。虛數位於垂直座標軸之上。
複數平面的圖示。虛數位於垂直座標軸之上。
 複數平面上乘以虛數單位表示旋轉九十度
複數平面上乘以虛數單位表示旋轉九十度
在幾何學上,複數平面的垂直軸表示虛數,它們與代表實數的水平軸垂直。查看虛數的方法之一是參考標準數線:往右側正幅度增長,往左側則負幅度減少。在x軸的0點處,往上升方向可繪製y軸的「正」虛數,然後向上增加;而「負」虛數則往下增加。這個垂直軸通常被稱為「虛軸」,並被表示為 ,Im,
,Im, ,或
,或 。
。
在該呈現圖示中,乘以–1對應於以原點為中心180度的旋轉。 的乘法對應於「逆時針」方向的90度旋轉,而方程式
的乘法對應於「逆時針」方向的90度旋轉,而方程式 可被解釋為,如果我們對原點應用兩個90度旋轉,則終了結果是單一個180度旋轉。注意,「順時針」方向的90度旋轉也滿足這種解釋。這反映了
可被解釋為,如果我們對原點應用兩個90度旋轉,則終了結果是單一個180度旋轉。注意,「順時針」方向的90度旋轉也滿足這種解釋。這反映了 也解出了方程
也解出了方程 。一般來說,乘以複數與以複數輻角圍繞原點的旋轉相同,然後按其大小進行縮放。
。一般來說,乘以複數與以複數輻角圍繞原點的旋轉相同,然後按其大小進行縮放。
我們應該將根號視為求 的解,故將一個數開根號後會有兩個合理的值,此二值互相差一個負號。在將正數開根號時,這兩個值一為正數一為負數,故習慣上直接將根號對應到正值,而負值的解以根號前加負號來表示。但對其它的數而言開根號沒有自然的對應,
的解,故將一個數開根號後會有兩個合理的值,此二值互相差一個負號。在將正數開根號時,這兩個值一為正數一為負數,故習慣上直接將根號對應到正值,而負值的解以根號前加負號來表示。但對其它的數而言開根號沒有自然的對應, 實際上代表的是兩個數,分別為
實際上代表的是兩個數,分別為 及
及 。但若直接將
。但若直接將 對應到
對應到 ,而
,而 對應到
對應到 也未嘗不可。
也未嘗不可。
1. 不同的虛數都是不能比較大小的: 成立,但
成立,但 和
和 卻均不成立。
卻均不成立。
舉例說明:(反證法)
假設
平方得
得 即可看出矛盾。
即可看出矛盾。
再舉例:假設
平方得 (不等式兩側同乘假設為負的
(不等式兩側同乘假設為負的 ,不等式由小於變為大於)
,不等式由小於變為大於)
得 即可看出矛盾。
即可看出矛盾。
因此虛數或者說虛部不爲0的複數不能比較大小。
2. 因爲 ,
, ,
, ,
, ,
, ,
, ,很容易知道
,很容易知道 (
( )是關於指數
)是關於指數 的週期函數,最小正週期是
的週期函數,最小正週期是 。於是,我們有
。於是,我們有

這表示 為方程
為方程 的一個根,另三個根分別為
的一個根,另三個根分別為 及
及 。
。
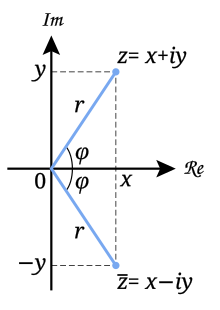
另外可以證明

和

爲下列方程的根


其中, 稱爲
稱爲 的共軛虛數(或共軛複數)。
的共軛虛數(或共軛複數)。
3. 如果再將虛數的這個概念擴展開去,就可以組成四元數(Quaternion)、八元數(Octonion)等特殊數學範疇。












![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)




![{\displaystyle \mathbb {Z} [\omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae955a9a0d0f342fc73aaafe28af604d23267f7)


























































