
In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.
In crystallography, a crystal system is a set of point groups. A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family.

In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group are the rigid transformations of an object that leave it unchanged. In three dimensions, space groups are classified into 219 distinct types, or 230 types if chiral copies are considered distinct. Space groups are discrete cocompact groups of isometries of an oriented Euclidean space in any number of dimensions. In dimensions other than 3, they are sometimes called Bieberbach groups.

In geometry and group theory, a lattice in the real coordinate space is an infinite set of points in this space with the properties that coordinate-wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension which spans the vector space . For any basis of , the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regular tiling of a space by a primitive cell.
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits.
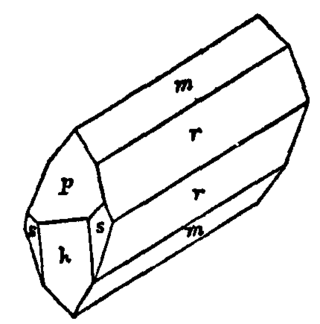
In crystallography, the monoclinic crystal system is one of the seven crystal systems. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism. Hence two pairs of vectors are perpendicular, while the third pair makes an angle other than 90°.
In crystallography, the orthorhombic crystal system is one of the 7 crystal systems. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.
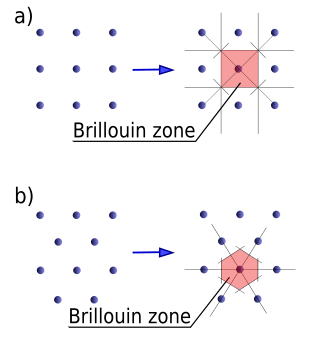
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice is broken up into Brillouin zones. The boundaries of this cell are given by planes related to points on the reciprocal lattice. The importance of the Brillouin zone stems from the description of waves in a periodic medium given by Bloch's theorem, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais (1850), is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
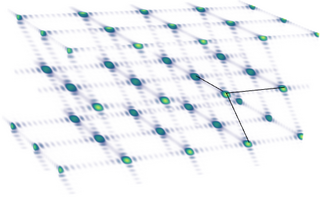
In physics, the reciprocal lattice represents the Fourier transform of another lattice. The direct lattice or real lattice is a periodic function in physical space, such as a crystal system. The reciprocal lattice exists in the mathematical space of spatial frequencies, known as reciprocal space or k space, where refers to the wavevector.

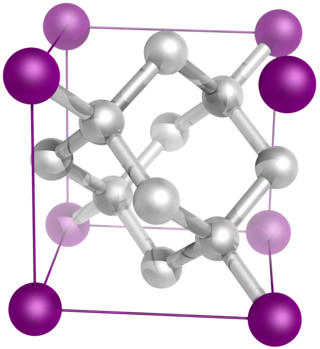
In crystallography, the cubiccrystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.

In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by a: Ta(p) = p + a.

Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.

The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in crystallography.
Born–von Karman boundary conditions are periodic boundary conditions which impose the restriction that a wave function must be periodic on a certain Bravais lattice. Named after Max Born and Theodore von Kármán, this condition is often applied in solid state physics to model an ideal crystal. Born and von Karman published a series of articles in 1912 and 1913 that presented one of the first theories of specific heat of solids based on the crystalline hypothesis and included these boundary conditions.

In solid-state physics and crystallography, a crystal structure is described by a unit cell. There are an infinite number of unit cells with different shapes and sizes which can describe the same crystal. Say that a crystal structure is described by a unit cell U. The supercell S of unit cell U is a cell which describes the same crystal, but has larger volume than cell U. Many methods which use a supercell perturbate it somehow to determine properties which cannot be determined by the initial cell. For example, during phonon calculations by the small displacement method, phonon frequencies in crystals are calculated using force values on slightly displaced atoms in the supercell. Another very important example of a supercell is the conventional cell of body-centered (bcc) or face-centered (fcc) cubic crystals.
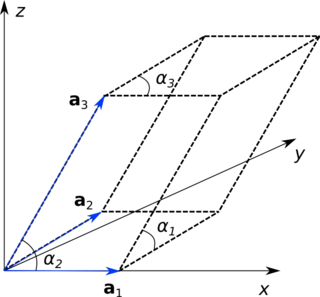
In crystallography, a fractional coordinate system is a coordinate system in which basis vectors used to the describe the space are the lattice vectors of a crystal (periodic) pattern. The selection of an origin and a basis define a unit cell, a parallelotope defined by the lattice basis vectors where is the dimension of the space. These basis vectors are described by lattice parameters consisting of the lengths of the lattice basis vectors and the angles between them .

In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems and two lattice systems. While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent. In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice.

In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron.
In solid state physics, the magnetic space groups, or Shubnikov groups, are the symmetry groups which classify the symmetries of a crystal both in space, and in a two-valued property such as electron spin. To represent such a property, each lattice point is colored black or white, and in addition to the usual three-dimensional symmetry operations, there is a so-called "antisymmetry" operation which turns all black lattice points white and all white lattice points black. Thus, the magnetic space groups serve as an extension to the crystallographic space groups which describe spatial symmetry alone.










































