| Regular tridecagon | |
|---|---|
 A regular tridecagon | |
| Type | Regular polygon |
| Edges and vertices | 13 |
| Schläfli symbol | {13} |
| Coxeter–Dynkin diagrams |    |
| Symmetry group | Dihedral (D13), order 2×13 |
| Internal angle (degrees) | ≈152.308° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.
A regular tridecagon is represented by Schläfli symbol {13}.
The measure of each internal angle of a regular tridecagon is approximately 152.308 degrees, and the area with side length a is given by
As 13 is a Pierpont prime but not a Fermat prime, the regular tridecagon cannot be constructed using a compass and straightedge. However, it is constructible using neusis, or an angle trisector.
The following is an animation from a neusis construction of a regular tridecagon with radius of circumcircle according to Andrew M. Gleason, [1] based on the angle trisection by means of the Tomahawk (light blue).
![A regular tridecagon (triskaidecagon) with radius of circumcircle
O
A
-
=
12
{\displaystyle {\overline {OA}}=12}
as an animation (1 min 44 s),
angle trisection by means of the Tomahawk (light blue). This construction is derived from the following equation:
12
cos
[?]
(
2
p
13
)
=
2
26
-
2
13
cos
[?]
(
1
3
arctan
[?]
(
3
(
13
+
1
)
7
-
13
)
)
+
13
-
1.
{\displaystyle 12\cos \left({\frac {2\pi }{13}}\right)=2{\sqrt {26-2{\sqrt {13}}}}\cos \left({\frac {1}{3}}\arctan \left({\frac {{\sqrt {3}}\left({\sqrt {13}}+1\right)}{7-{\sqrt {13}}}}\right)\right)+{\sqrt {13}}-1.} 01-Triskaidecagon-Animation.gif](http://upload.wikimedia.org/wikipedia/commons/thumb/5/52/01-Triskaidecagon-Animation.gif/700px-01-Triskaidecagon-Animation.gif)
An approximate construction of a regular tridecagon using straightedge and compass is shown here.
Another possible animation of an approximate construction, also possible with using straightedge and compass.
At a circumscribed circle of radius r = 1 billion km (a distance which would take light approximately 55 minutes to travel), the absolute error on the side length constructed would be less than 1 mm.
The regular tridecagon has Dih13 symmetry, order 26. Since 13 is a prime number there is one subgroup with dihedral symmetry: Dih1, and 2 cyclic group symmetries: Z13, and Z1.
These 4 symmetries can be seen in 4 distinct symmetries on the tridecagon. John Conway labels these by a letter and group order. [2] Full symmetry of the regular form is r26 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g13 subgroup has no degrees of freedom but can be seen as directed edges.
The regular tridecagon is used as the shape of the Czech 20 korun coin. [3]
A tridecagram is a 13-sided star polygon. There are 5 regular forms given by Schläfli symbols: {13/2}, {13/3}, {13/4}, {13/5}, and {13/6}. Since 13 is prime, none of the tridecagrams are compound figures. Culturally, this shape is a symbol for immortality.
Yellow tridecagrams appear in a video for the song "Mesmerizer".
| Tridecagrams | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Picture |  {13/2} |  {13/3} |  {13/4} |  {13/5} |  {13/6} | ||||||
| Internal angle | ≈124.615° | ≈96.9231° | ≈69.2308° | ≈41.5385° | ≈13.8462° | ||||||
The regular tridecagon is the Petrie polygon 12-simplex:
| A12 |
|---|
 12-simplex |
In geometry and algebra, a real number is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.
Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.
In geometry, an octagon is an eight-sided polygon or 8-gon.
In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.
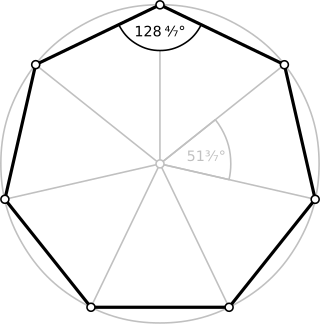
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
In geometry, a nonagon or enneagon is a nine-sided polygon or 9-gon.
In geometry, an icosagon or 20-gon is a twenty-sided polygon. The sum of any icosagon's interior angles is 3240 degrees.
In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.
In geometry, a chiliagon or 1,000-gon is a polygon with 1,000 sides. Philosophers commonly refer to chiliagons to illustrate ideas about the nature and workings of thought, meaning, and mental representation.
In geometry, a myriagon or 10000-gon is a polygon with 10000 sides. Several philosophers have used the regular myriagon to illustrate issues regarding thought.
In geometry, a hendecagon or 11-gon is an eleven-sided polygon.
In geometry, a triacontagon or 30-gon is a thirty-sided polygon. The sum of any triacontagon's interior angles is 5040 degrees.
In geometry, a pentadecagon or pentakaidecagon or 15-gon is a fifteen-sided polygon.
In geometry, the neusis is a geometric construction method that was used in antiquity by Greek mathematicians.
In geometry, a 65537-gon is a polygon with 65,537 (216 + 1) sides. The sum of the interior angles of any non–self-intersecting 65537-gon is 11796300°.
In geometry, a tetradecagon or tetrakaidecagon or 14-gon is a fourteen-sided polygon.
In geometry, a pentagon is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
In geometry, an icositrigon or 23-gon is a 23-sided polygon. The icositrigon has the distinction of being the smallest regular polygon that is not neusis constructible.
