A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical tone. Vibrating strings are the basis of string instruments such as guitars, cellos, and pianos.
The velocity of propagation of a wave in a string () is proportional to the square root of the force of tension of the string () and inversely proportional to the square root of the linear density () of the string:
This relationship was discovered by Vincenzo Galilei in the late 1500s. [ citation needed ]
Source: [1]
Let be the length of a piece of string, its mass, and its linear density. If angles and are small, then the horizontal components of tension on either side can both be approximated by a constant , for which the net horizontal force is zero. Accordingly, using the small angle approximation, the horizontal tensions acting on both sides of the string segment are given by
From Newton's second law for the vertical component, the mass (which is the product of its linear density and length) of this piece times its acceleration, , will be equal to the net force on the piece:
Dividing this expression by and substituting the first and second equations obtains (we can choose either the first or the second equation for , so we conveniently choose each one with the matching angle and )
According to the small-angle approximation, the tangents of the angles at the ends of the string piece are equal to the slopes at the ends, with an additional minus sign due to the definition of and . Using this fact and rearranging provides
In the limit that approaches zero, the left hand side is the definition of the second derivative of :
This is the wave equation for , and the coefficient of the second time derivative term is equal to ; thus
Where is the speed of propagation of the wave in the string (see the article on the wave equation for more about this). However, this derivation is only valid for small amplitude vibrations; for those of large amplitude, is not a good approximation for the length of the string piece, the horizontal component of tension is not necessarily constant. The horizontal tensions are not well approximated by .
Once the speed of propagation is known, the frequency of the sound produced by the string can be calculated. The speed of propagation of a wave is equal to the wavelength divided by the period , or multiplied by the frequency :
If the length of the string is , the fundamental harmonic is the one produced by the vibration whose nodes are the two ends of the string, so is half of the wavelength of the fundamental harmonic. Hence one obtains Mersenne's laws:
where is the tension (in Newtons), is the linear density (that is, the mass per unit length), and is the length of the vibrating part of the string. Therefore:
Moreover, if we take the nth harmonic as having a wavelength given by , then we easily get an expression for the frequency of the nth harmonic:
And for a string under a tension T with linear density , then
One can see the waveforms on a vibrating string if the frequency is low enough and the vibrating string is held in front of a CRT screen such as one of a television or a computer (not of an analog oscilloscope). This effect is called the stroboscopic effect, and the rate at which the string seems to vibrate is the difference between the frequency of the string and the refresh rate of the screen. The same can happen with a fluorescent lamp, at a rate that is the difference between the frequency of the string and the frequency of the alternating current. (If the refresh rate of the screen equals the frequency of the string or an integer multiple thereof, the string will appear still but deformed.) In daylight and other non-oscillating light sources, this effect does not occur and the string appears still but thicker, and lighter or blurred, due to persistence of vision.
A similar but more controllable effect can be obtained using a stroboscope. This device allows matching the frequency of the xenon flash lamp to the frequency of vibration of the string. In a dark room, this clearly shows the waveform. Otherwise, one can use bending or, perhaps more easily, by adjusting the machine heads, to obtain the same, or a multiple, of the AC frequency to achieve the same effect. For example, in the case of a guitar, the 6th (lowest pitched) string pressed to the third fret gives a G at 97.999 Hz. A slight adjustment can alter it to 100 Hz, exactly one octave above the alternating current frequency in Europe and most countries in Africa and Asia, 50 Hz. In most countries of the Americas—where the AC frequency is 60 Hz—altering A# on the fifth string, first fret from 116.54 Hz to 120 Hz produces a similar effect.
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
In numerical analysis, the Clenshaw algorithm, also called Clenshaw summation, is a recursive method to evaluate a linear combination of Chebyshev polynomials. The method was published by Charles William Clenshaw in 1955. It is a generalization of Horner's method for evaluating a linear combination of monomials.
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the linear rotor requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water, ammonia, or methane.
In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.
In electromagnetism, the electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field in spacetime. The field tensor was first used after the four-dimensional tensor formulation of special relativity was introduced by Hermann Minkowski. The tensor allows related physical laws to be written concisely, and allows for the quantization of the electromagnetic field by the Lagrangian formulation described below.
In general relativity, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein–Hilbert action when the underlying spacetime manifold has a boundary.
The Duffing equation, named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by where the (unknown) function is the displacement at time t, is the first derivative of with respect to time, i.e. velocity, and is the second time-derivative of i.e. acceleration. The numbers and are given constants.
A theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the Earth. A key advantage in examining circular orbits is that it is possible to know the solution of the Einstein Field Equation a priori. This provides a means to inform and verify the formalism.
In relativistic physics, the electromagnetic stress–energy tensor is the contribution to the stress–energy tensor due to the electromagnetic field. The stress–energy tensor describes the flow of energy and momentum in spacetime. The electromagnetic stress–energy tensor contains the negative of the classical Maxwell stress tensor that governs the electromagnetic interactions.
The covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form that is manifestly invariant under Lorentz transformations, in the formalism of special relativity using rectilinear inertial coordinate systems. These expressions both make it simple to prove that the laws of classical electromagnetism take the same form in any inertial coordinate system, and also provide a way to translate the fields and forces from one frame to another. However, this is not as general as Maxwell's equations in curved spacetime or non-rectilinear coordinate systems.
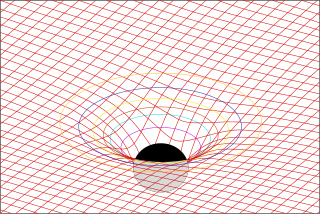
In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.
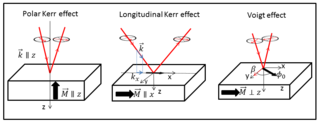
The Voigt effect is a magneto-optical phenomenon which rotates and elliptizes linearly polarised light sent into an optically active medium. The effect is named after the German scientist Woldemar Voigt who discovered it in vapors. Unlike many other magneto-optical effects such as the Kerr or Faraday effect which are linearly proportional to the magnetization, the Voigt effect is proportional to the square of the magnetization and can be seen experimentally at normal incidence. There are also other denominations for this effect, used interchangeably in the modern scientific literature: the Cotton–Mouton effect and magnetic-linear birefringence, with the latter reflecting the physical meaning of the effect.
Acoustic streaming is a steady flow in a fluid driven by the absorption of high amplitude acoustic oscillations. This phenomenon can be observed near sound emitters, or in the standing waves within a Kundt's tube. Acoustic streaming was explained first by Lord Rayleigh in 1884. It is the less-known opposite of sound generation by a flow.
Experimental uncertainty analysis is a technique that analyses a derived quantity, based on the uncertainties in the experimentally measured quantities that are used in some form of mathematical relationship ("model") to calculate that derived quantity. The model used to convert the measurements into the derived quantity is usually based on fundamental principles of a science or engineering discipline.
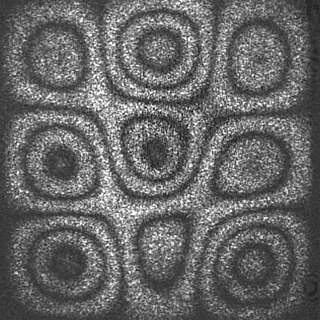
The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This permits a two-dimensional plate theory to give an excellent approximation to the actual three-dimensional motion of a plate-like object.
In theoretical physics, the dual graviton is a hypothetical elementary particle that is a dual of the graviton under electric-magnetic duality, as an S-duality, predicted by some formulations of eleven-dimensional supergravity.
| Acoustical engineering | ||
|---|---|---|
| Psychoacoustics | ||
| Audio frequency and pitch | ||
| Acousticians | ||
| Related topics | ||
