
A regular expression, sometimes referred to as rational expression, is a sequence of characters that specifies a match pattern in text. Usually such patterns are used by string-searching algorithms for "find" or "find and replace" operations on strings, or for input validation. Regular expression techniques are developed in theoretical computer science and formal language theory.

In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed. A string is generally considered as a data type and is often implemented as an array data structure of bytes that stores a sequence of elements, typically characters, using some character encoding. String may also denote more general arrays or other sequence data types and structures.
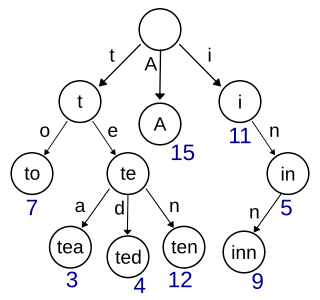
In computer science, a trie, also known as a digital tree or prefix tree, is a specialized search tree data structure used to store and retrieve strings from a dictionary or set. Unlike a binary search tree, nodes in a trie do not store their associated key. Instead, each node's position within the trie determines its associated key, with the connections between nodes defined by individual characters rather than the entire key.
The Burrows–Wheeler transform rearranges a character string into runs of similar characters. This is useful for compression, since it tends to be easy to compress a string that has runs of repeated characters by techniques such as move-to-front transform and run-length encoding. More importantly, the transformation is reversible, without needing to store any additional data except the position of the first original character. The BWT is thus a "free" method of improving the efficiency of text compression algorithms, costing only some extra computation. The Burrows–Wheeler transform is an algorithm used to prepare data for use with data compression techniques such as bzip2. It was invented by Michael Burrows and David Wheeler in 1994 while Burrows was working at DEC Systems Research Center in Palo Alto, California. It is based on a previously unpublished transformation discovered by Wheeler in 1983. The algorithm can be implemented efficiently using a suffix array thus reaching linear time complexity.

In computer science, the Aho–Corasick algorithm is a string-searching algorithm invented by Alfred V. Aho and Margaret J. Corasick in 1975. It is a kind of dictionary-matching algorithm that locates elements of a finite set of strings within an input text. It matches all strings simultaneously. The complexity of the algorithm is linear in the length of the strings plus the length of the searched text plus the number of output matches. Note that because all matches are found, multiple matches will be returned for one string location if multiple substrings matched.
In computer science, the Knuth–Morris–Pratt algorithm is a string-searching algorithm that searches for occurrences of a "word" W within a main "text string" S by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.
In computational linguistics and computer science, edit distance is a string metric, i.e. a way of quantifying how dissimilar two strings are to one another, that is measured by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T.
In biology, a sequence motif is a nucleotide or amino-acid sequence pattern that is widespread and usually assumed to be related to biological function of the macromolecule. For example, an N-glycosylation site motif can be defined as Asn, followed by anything but Pro, followed by either Ser or Thr, followed by anything but Pro residue.
In computer science, the Boyer–Moore string-search algorithm is an efficient string-searching algorithm that is the standard benchmark for practical string-search literature. It was developed by Robert S. Boyer and J Strother Moore in 1977. The original paper contained static tables for computing the pattern shifts without an explanation of how to produce them. The algorithm for producing the tables was published in a follow-on paper; this paper contained errors which were later corrected by Wojciech Rytter in 1980.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.
In computer science, the Boyer–Moore–Horspool algorithm or Horspool's algorithm is an algorithm for finding substrings in strings. It was published by Nigel Horspool in 1980 as SBM.

In computer science, approximate string matching is the technique of finding strings that match a pattern approximately. The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring matches inside a given string and finding dictionary strings that match the pattern approximately.
In computational phylogenetics, tree alignment is a computational problem concerned with producing multiple sequence alignments, or alignments of three or more sequences of DNA, RNA, or protein. Sequences are arranged into a phylogenetic tree, modeling the evolutionary relationships between species or taxa. The edit distances between sequences are calculated for each of the tree's internal vertices, such that the sum of all edit distances within the tree is minimized. Tree alignment can be accomplished using one of several algorithms with various trade-offs between manageable tree size and computational effort.
In computer science, the Apostolico–Giancarlo algorithm is a variant of the Boyer–Moore string-search algorithm, the basic application of which is searching for occurrences of a pattern in a text . As with other comparison-based string searches, this is done by aligning to a certain index of and checking whether a match occurs at that index. is then shifted relative to according to the rules of the Boyer–Moore algorithm, and the process repeats until the end of has been reached. Application of the Boyer–Moore shift rules often results in large chunks of the text being skipped entirely.
In computer science, compressed pattern matching is the process of searching for patterns in compressed data with little or no decompression. Searching in a compressed string is faster than searching an uncompressed string and requires less space.
In computer science, an FM-index is a compressed full-text substring index based on the Burrows–Wheeler transform, with some similarities to the suffix array. It was created by Paolo Ferragina and Giovanni Manzini, who describe it as an opportunistic data structure as it allows compression of the input text while still permitting fast substring queries. The name stands for Full-text index in Minute space.
In computer science, a compressed suffix array is a compressed data structure for pattern matching. Compressed suffix arrays are a general class of data structure that improve on the suffix array. These data structures enable quick search for an arbitrary string with a comparatively small index.
In machine learning and data mining, a string kernel is a kernel function that operates on strings, i.e. finite sequences of symbols that need not be of the same length. String kernels can be intuitively understood as functions measuring the similarity of pairs of strings: the more similar two strings a and b are, the higher the value of a string kernel K(a, b) will be.
In computer science, the two-way string-matching algorithm is a string-searching algorithm, discovered by Maxime Crochemore and Dominique Perrin in 1991. It takes a pattern of size m, called a “needle”, preprocesses it in linear time O(m), producing information that can then be used to search for the needle in any “haystack” string, taking only linear time O(n) with n being the haystack's length.









