Related Research Articles
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology, oceanography, geochemistry, geometallurgy, geography, forestry, environmental control, landscape ecology, soil science, and agriculture. Geostatistics is applied in varied branches of geography, particularly those involving the spread of diseases (epidemiology), the practice of commerce and military planning (logistics), and the development of efficient spatial networks. Geostatistical algorithms are incorporated in many places, including geographic information systems (GIS).
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by , is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the p-value of a result, , is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when . The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study.
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm.
Bayesian statistics is a theory in the field of statistics based on the Bayesian interpretation of probability where probability expresses a degree of belief in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation that views probability as the limit of the relative frequency of an event after many trials.
In statistics, exploratory data analysis (EDA) is an approach of analyzing data sets to summarize their main characteristics, often using statistical graphics and other data visualization methods. A statistical model can be used or not, but primarily EDA is for seeing what the data can tell us beyond the formal modeling and thereby contrasts traditional hypothesis testing. Exploratory data analysis has been promoted by John Tukey since 1970 to encourage statisticians to explore the data, and possibly formulate hypotheses that could lead to new data collection and experiments. EDA is different from initial data analysis (IDA), which focuses more narrowly on checking assumptions required for model fitting and hypothesis testing, and handling missing values and making transformations of variables as needed. EDA encompasses IDA.

Calyampudi Radhakrishna Rao,, commonly known as C. R. Rao, is an Indian-American mathematician and statistician. He is currently professor emeritus at Pennsylvania State University and Research Professor at the University at Buffalo. Rao has been honoured by numerous colloquia, honorary degrees, and festschrifts and was awarded the US National Medal of Science in 2002. The American Statistical Association has described him as "a living legend whose work has influenced not just statistics, but has had far reaching implications for fields as varied as economics, genetics, anthropology, geology, national planning, demography, biometry, and medicine." The Times of India listed Rao as one of the top 10 Indian scientists of all time. Rao is also a Senior Policy and Statistics advisor for the Indian Heart Association non-profit focused on raising South Asian cardiovascular disease awareness.

Sir David Roxbee Cox was a British statistician and educator. His wide-ranging contributions to the field of statistics included introducing logistic regression, the proportional hazards model and the Cox process, a point process named after him.
In robust statistics, robust regression seeks to overcome some limitations of traditional regression analysis. A regression analysis models the relationship between one or more independent variables and a dependent variable. Standard types of regression, such as ordinary least squares, have favourable properties if their underlying assumptions are true, but can give misleading results otherwise. Robust regression methods are designed to limit the effect that violations of assumptions by the underlying data-generating process have on regression estimates.

Spatial analysis is any of the formal techniques which studies entities using their topological, geometric, or geographic properties. Spatial analysis includes a variety of techniques using different analytic approaches, especially spatial statistics. In may be applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, or to chip fabrication engineering, with its use of "place and route" algorithms to build complex wiring structures. In a more restricted sense, spatial analysis is geospatial analysis, the technique applied to structures at the human scale, most notably in the analysis of geographic data. It may also be applied to genomics, as in transcriptomics data.
In applied mathematics, the Wiener–Khinchin theorem or Wiener–Khintchine theorem, also known as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem, states that the autocorrelation function of a wide-sense-stationary random process has a spectral decomposition given by the power spectrum of that process.
In statistics, sequential analysis or sequential hypothesis testing is statistical analysis where the sample size is not fixed in advance. Instead data are evaluated as they are collected, and further sampling is stopped in accordance with a pre-defined stopping rule as soon as significant results are observed. Thus a conclusion may sometimes be reached at a much earlier stage than would be possible with more classical hypothesis testing or estimation, at consequently lower financial and/or human cost.
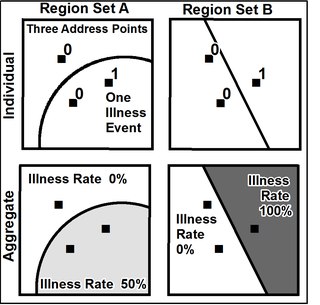
The modifiable areal unit problem (MAUP) is a source of statistical bias that can significantly impact the results of statistical hypothesis tests. MAUP affects results when point-based measures of spatial phenomena are aggregated into spatial partitions or areal units as in, for example, population density or illness rates. The resulting summary values are influenced by both the shape and scale of the aggregation unit.
Spatial epidemiology is a subfield of epidemiology focused on the study of the spatial distribution of health outcomes; it is closely related to health geography.
Joseph Michael Hilbe was an American statistician and philosopher, founding President of the International Astrostatistics Association(IAA) and one of the most prolific authors of books on statistical modeling in the early twenty-first century. Hilbe was an elected Fellow of the American Statistical Association as well as an elected member of the International Statistical Institute (ISI), for which he founded the ISI astrostatistics committee in 2009. Hilbe was also a Fellow of the Royal Statistical Society and Full Member of the American Astronomical Society.
A boundary problem in analysis is a phenomenon in which geographical patterns are differentiated by the shape and arrangement of boundaries that are drawn for administrative or measurement purposes. The boundary problem occurs because of the loss of neighbors in analyses that depend on the values of the neighbors. While geographic phenomena are measured and analyzed within a specific unit, identical spatial data can appear either dispersed or clustered depending on the boundary placed around the data. In analysis with point data, dispersion is evaluated as dependent of the boundary. In analysis with areal data, statistics should be interpreted based upon the boundary.

In probability, statistics and related fields, a Poisson point process is a type of random mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The Poisson point process is often called simply the Poisson process, but it is also called a Poisson random measure, Poisson random point field or Poisson point field. This point process has convenient mathematical properties, which has led to its being frequently defined in Euclidean space and used as a mathematical model for seemingly random processes in numerous disciplines such as astronomy, biology, ecology, geology, seismology, physics, economics, image processing, and telecommunications.

The growth curve model in statistics is a specific multivariate linear model, also known as GMANOVA. It generalizes MANOVA by allowing post-matrices, as seen in the definition.
Sudipto Banerjee is an Indian-American statistician best known for his work on Bayesian hierarchical modeling and inference for spatial data analysis. He is Professor and Chair of the Department of Biostatistics in the School of Public Health at the University of California, Los Angeles. He served as the 2022 President of the International Society for Bayesian Analysis.
Noel Andrew Cressie is an Australian and American statistician. He is Distinguished Professor and Director, Centre for Environmental Informatics, at the University of Wollongong in Wollongong, Australia.
References
- ↑ Ripley, B.D. (2005). Spatial Statistics. Wiley Series in Probability and Statistics. Wiley. ISBN 978-0-471-72520-6 . Retrieved 2023-04-04.
- ↑ van Lieshout, M.N.M. (2019). Theory of Spatial Statistics: A Concise Introduction. Chapman & Hall/CRC Texts in Statistical Science. CRC Press. ISBN 978-0-429-62867-2 . Retrieved 2023-04-04.
- ↑ Cressie, N. (2015). Statistics for Spatial Data. Wiley Series in Probability and Statistics. Wiley. ISBN 978-1-119-11518-2 . Retrieved 2023-04-04.
- ↑ Gelfand, A.E.; Diggle, P.; Guttorp, P.; Fuentes, M. (2010). Handbook of Spatial Statistics. Chapman & Hall/CRC Handbooks of Modern Statistical Methods. CRC Press. ISBN 978-1-4200-7288-4 . Retrieved 2023-04-04.