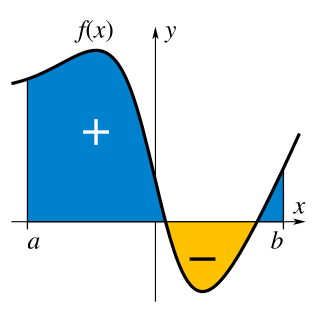
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.
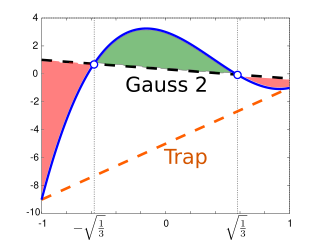
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration. An n-point Gaussian quadrature rule, named after Carl Friedrich Gauss, is a quadrature rule constructed to yield an exact result for polynomials of degree 2n − 1 or less by a suitable choice of the nodes xi and weights wi for i = 1, …, n. The modern formulation using orthogonal polynomials was developed by Carl Gustav Jacobi in 1826. The most common domain of integration for such a rule is taken as [−1, 1], so the rule is stated as

In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of definite integrals.

In numerical analysis, the Newton–Cotes formulas, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulas for numerical integration based on evaluating the integrand at equally spaced points. They are named after Isaac Newton and Roger Cotes.
The VEGAS algorithm, due to G. Peter Lepage, is a method for reducing error in Monte Carlo simulations by using a known or approximate probability distribution function to concentrate the search in those areas of the integrand that make the greatest contribution to the final integral.
Basic Linear Algebra Subprograms (BLAS) is a specification that prescribes a set of low-level routines for performing common linear algebra operations such as vector addition, scalar multiplication, dot products, linear combinations, and matrix multiplication. They are the de facto standard low-level routines for linear algebra libraries; the routines have bindings for both C and Fortran. Although the BLAS specification is general, BLAS implementations are often optimized for speed on a particular machine, so using them can bring substantial performance benefits. BLAS implementations will take advantage of special floating point hardware such as vector registers or SIMD instructions.
The GNU Scientific Library is a software library for numerical computations in applied mathematics and science. The GSL is written in C; wrappers are available for other programming languages. The GSL is part of the GNU Project and is distributed under the GNU General Public License.

Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.
Adaptive Simpson's method, also called adaptive Simpson's rule, is a method of numerical integration proposed by G.F. Kuncir in 1962. It is probably the first recursive adaptive algorithm for numerical integration to appear in print, although more modern adaptive methods based on Gauss–Kronrod quadrature and Clenshaw–Curtis quadrature are now generally preferred. Adaptive Simpson's method uses an estimate of the error we get from calculating a definite integral using Simpson's rule. If the error exceeds a user-specified tolerance, the algorithm calls for subdividing the interval of integration in two and applying adaptive Simpson's method to each subinterval in a recursive manner. The technique is usually much more efficient than composite Simpson's rule since it uses fewer function evaluations in places where the function is well-approximated by a cubic function.
Clenshaw–Curtis quadrature and Fejér quadrature are methods for numerical integration, or "quadrature", that are based on an expansion of the integrand in terms of Chebyshev polynomials. Equivalently, they employ a change of variables and use a discrete cosine transform (DCT) approximation for the cosine series. Besides having fast-converging accuracy comparable to Gaussian quadrature rules, Clenshaw–Curtis quadrature naturally leads to nested quadrature rules, which is important for both adaptive quadrature and multidimensional quadrature (cubature).
Adaptive quadrature is a numerical integration method in which the integral of a function is approximated using static quadrature rules on adaptively refined subintervals of the region of integration. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well behaved" integrands, but are also effective for "badly behaved" integrands for which traditional algorithms may fail.
Tanh-sinh quadrature is a method for numerical integration introduced by Hidetoshi Takahashi and Masatake Mori in 1974. It is especially applied where singularities or infinite derivatives exist at one or both endpoints.
The Gauss–Kronrod quadrature formula is an adaptive method for numerical integration. It is a variant of Gaussian quadrature, in which the evaluation points are chosen so that an accurate approximation can be computed by re-using the information produced by the computation of a less accurate approximation. It is an example of what is called a nested quadrature rule: for the same set of function evaluation points, it has two quadrature rules, one higher order and one lower order. The difference between these two approximations is used to estimate the calculational error of the integration.
In numerical analysis Gauss–Laguerre quadrature is an extension of the Gaussian quadrature method for approximating the value of integrals of the following kind:
SLATEC Common Mathematical Library is a FORTRAN 77 library of over 1400 general purpose mathematical and statistical routines. The code was developed at US Government research laboratories and is therefore public domain software.
GPOPS-II is a general-purpose MATLAB software for solving continuous optimal control problems using hp-adaptive Gaussian quadrature collocation and sparse nonlinear programming. The acronym GPOPS stands for "General Purpose OPtimal Control Software", and the Roman numeral "II" refers to the fact that GPOPS-II is the second software of its type.
Bayesian quadrature is a numerical method for solving numerical integration problems which falls within the class of probabilistic numerical methods. Bayesian quadrature views numerical integration as a Bayesian inference task, where function evaluations are used to estimate the integral of that function. For this reason, it is sometimes also referred to as "Bayesian probabilistic numerical integration" or "Bayesian numerical integration". The name "Bayesian cubature" is also sometimes used when the integrand is multi-dimensional. A potential advantage of this approach is that it provides probabilistic uncertainty quantification for the value of the integral.







