In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering. The pseudopotential approximation was first introduced by Hans Hellmann in 1934. [1]
The pseudopotential is an attempt to replace the complicated effects of the motion of the core (i.e. non-valence) electrons of an atom and its nucleus with an effective potential, or pseudopotential, so that the Schrödinger equation contains a modified effective potential term instead of the Coulombic potential term for core electrons normally found in the Schrödinger equation.
The pseudopotential is an effective potential constructed to replace the atomic all-electron potential (full-potential) such that core states are eliminated and the valence electrons are described by pseudo-wavefunctions with significantly fewer nodes. This allows the pseudo-wavefunctions to be described with far fewer Fourier modes, thus making plane-wave basis sets practical to use. In this approach usually only the chemically active valence electrons are dealt with explicitly, while the core electrons are 'frozen', being considered together with the nuclei as rigid non-polarizable ion cores. It is possible to self-consistently update the pseudopotential with the chemical environment that it is embedded in, having the effect of relaxing the frozen core approximation, although this is rarely done. In codes using local basis functions, like Gaussian, often effective core potentials are used that only freeze the core electrons.
First-principles pseudopotentials are derived from an atomic reference state, requiring that the pseudo- and all-electron valence eigenstates have the same energies and amplitude (and thus density) outside a chosen core cut-off radius .
Pseudopotentials with larger cut-off radius are said to be softer, that is more rapidly convergent, but at the same time less transferable, that is less accurate to reproduce realistic features in different environments.
Motivation:
Approximations:
Early applications of pseudopotentials to atoms and solids based on attempts to fit atomic spectra achieved only limited success. Solid-state pseudopotentials achieved their present popularity largely because of the successful fits by Walter Harrison to the nearly free electron Fermi surface of aluminum (1958) and by James C. Phillips to the covalent energy gaps of silicon and germanium (1958). Phillips and coworkers (notably Marvin L. Cohen and coworkers) later extended this work to many other semiconductors, in what they called "semiempirical pseudopotentials". [4]
Norm-conserving and ultrasoft are the two most common forms of pseudopotential used in modern plane-wave electronic structure codes. They allow a basis-set with a significantly lower cut-off (the frequency of the highest Fourier mode) to be used to describe the electron wavefunctions and so allow proper numerical convergence with reasonable computing resources. An alternative would be to augment the basis set around nuclei with atomic-like functions, as is done in LAPW. Norm-conserving pseudopotential was first proposed by Hamann, Schlüter, and Chiang (HSC) in 1979. [5] The original HSC norm-conserving pseudopotential takes the following form:
where projects a one-particle wavefunction, such as one Kohn-Sham orbital, to the angular momentum labeled by . is the pseudopotential that acts on the projected component. Different angular momentum states then feel different potentials, thus the HSC norm-conserving pseudopotential is non-local, in contrast to local pseudopotential which acts on all one-particle wave-functions in the same way.
Norm-conserving pseudopotentials are constructed to enforce two conditions.
1. Inside the cut-off radius , the norm of each pseudo-wavefunction be identical to its corresponding all-electron wavefunction: [6]
2. All-electron and pseudo wavefunctions are identical outside cut-off radius .
Ultrasoft pseudopotentials relax the norm-conserving constraint to reduce the necessary basis-set size further at the expense of introducing a generalized eigenvalue problem. [7] With a non-zero difference in norms we can now define:
and so a normalised eigenstate of the pseudo Hamiltonian now obeys the generalized equation
where the operator is defined as
where are projectors that form a dual basis with the pseudo reference states inside the cut-off radius, and are zero outside:
A related technique [8] is the projector augmented wave (PAW) method.
Enrico Fermi introduced a pseudopotential, , to describe the scattering of a free neutron by a nucleus. [9] The scattering is assumed to be s-wave scattering, and therefore spherically symmetric. Therefore, the potential is given as a function of radius, :
where is the Planck constant divided by , is the mass, is the Dirac delta function, is the bound coherent neutron scattering length, and the center of mass of the nucleus. [10] The Fourier transform of this -function leads to the constant neutron form factor.
James Charles Phillips developed a simplified pseudopotential while at Bell Labs useful for describing silicon and germanium. [11]
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense fervent in the development of quantum mechanics.
Density functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier in 1937. Wannier functions are the localized molecular orbitals of crystalline systems.
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset.
The diabatic representation as a mathematical tool for theoretical calculations of atomic collisions and of molecular interactions.
Time-dependent density-functional theory (TDDFT) is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.
In quantum mechanics, the exchange operator, also known as permutation operator, is a quantum mechanical operator that acts on states in Fock space. The exchange operator acts by switching the labels on any two identical particles described by the joint position quantum state . Since the particles are identical, the notion of exchange symmetry requires that the exchange operator be unitary.
The Gross–Pitaevskii equation describes the ground state of a quantum system of identical bosons using the Hartree–Fock approximation and the pseudopotential interaction model.
Within computational chemistry, the Slater–Condon rules express integrals of one- and two-body operators over wavefunctions constructed as Slater determinants of orthonormal orbitals in terms of the individual orbitals. In doing so, the original integrals involving N-electron wavefunctions are reduced to sums over integrals involving at most two molecular orbitals, or in other words, the original 3N dimensional integral is expressed in terms of many three- and six-dimensional integrals.
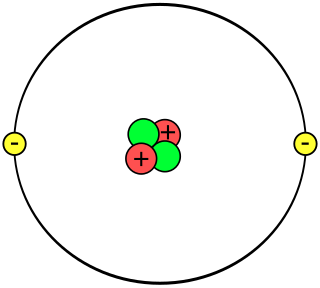
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.
In physics, Berry connection and Berry curvature are related concepts which can be viewed, respectively, as a local gauge potential and gauge field associated with the Berry phase or geometric phase. The concept was first introduced by S. Pancharatnam as geometric phase and later elaborately explained and popularized by Michael Berry in a paper published in 1984 emphasizing how geometric phases provide a powerful unifying concept in several branches of classical and quantum physics.
In quantum mechanics, orbital magnetization, Morb, refers to the magnetization induced by orbital motion of charged particles, usually electrons in solids. The term "orbital" distinguishes it from the contribution of spin degrees of freedom, Mspin, to the total magnetization. A nonzero orbital magnetization requires broken time-reversal symmetry, which can occur spontaneously in ferromagnetic and ferrimagnetic materials, or can be induced in a non-magnetic material by an applied magnetic field.
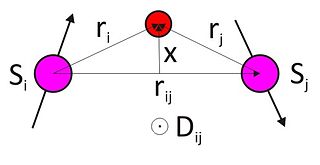
In Physics, antisymmetric exchange, also known as the Dzyaloshinskii–Moriya interaction (DMI), is a contribution to the total magnetic exchange interaction between two neighboring magnetic spins, and . Quantitatively, it is a term in the Hamiltonian which can be written as
The projector augmented wave method (PAW) is a technique used in ab initio electronic structure calculations. It is a generalization of the pseudopotential and linear augmented-plane-wave methods, and allows for density functional theory calculations to be performed with greater computational efficiency.
Surface hopping is a mixed quantum-classical technique that incorporates quantum mechanical effects into molecular dynamics simulations. Traditional molecular dynamics assume the Born-Oppenheimer approximation, where the lighter electrons adjust instantaneously to the motion of the nuclei. Though the Born-Oppenheimer approximation is applicable to a wide range of problems, there are several applications, such as photoexcited dynamics, electron transfer, and surface chemistry where this approximation falls apart. Surface hopping partially incorporates the non-adiabatic effects by including excited adiabatic surfaces in the calculations, and allowing for 'hops' between these surfaces, subject to certain criteria.
The Peierls substitution method, named after the original work by Rudolf Peierls is a widely employed approximation for describing tightly-bound electrons in the presence of a slowly varying magnetic vector potential.
In solid state physics, the Luttinger–Ward functional, proposed by Joaquin Mazdak Luttinger and John Clive Ward in 1960, is a scalar functional of the bare electron-electron interaction and the renormalized one-particle propagator. In terms of Feynman diagrams, the Luttinger–Ward functional is the sum of all closed, bold, two-particle irreducible diagrams, i.e., all diagrams without particles going in or out that do not fall apart if one removes two propagator lines. It is usually written as or , where is the one-particle Green's function and is the bare interaction.
In quantum computing, Mølmer–Sørensen gate scheme refers to an implementation procedure for various multi-qubit quantum logic gates used mostly in trapped ion quantum computing. This procedure is based on the original proposition by Klaus Mølmer and Anders Sørensen in 1999-2000.
The linearized augmented-plane-wave method (LAPW) is an implementation of Kohn-Sham density functional theory (DFT) adapted to periodic materials. It typically goes along with the treatment of both valence and core electrons on the same footing in the context of DFT and the treatment of the full potential and charge density without any shape approximation. This is often referred to as the all-electron full-potential linearized augmented-plane-wave method (FLAPW). It does not rely on the pseudopotential approximation and employs a systematically extendable basis set. These features make it one of the most precise implementations of DFT, applicable to all crystalline materials, regardless of their chemical composition. It can be used as a reference for evaluating other approaches.
