Operation of computed tomography

Spiral computed tomography
Spiral computed tomography
MeSH	D036542

Last updated November 27, 2022

CT scanner with cover removed to show internal components. Legend:
T: X-ray tube
D: X-ray detectors
X: X-ray beam
R: Gantry rotation Ct-internals.jpg — CT scanner with cover removed to show internal components. Legend:
T: X-ray tube
D: X-ray detectors
X: X-ray beam
R: Gantry rotation

X-ray computed tomography operates by using an X-ray generator that rotates around the object; X-ray detectors are positioned on the opposite side of the circle from the X-ray source.

Structure
Contrast media
Schematic configuration and motion
Statements
Motion of parallel beam irradiation optical system
Increment/Table speed
Obtaining transmission image ‘s’
Tomographic reconstruction
Basic principle
Spiral CT
Single-slice and multi-slice Spiral CT
Pitch
Helical (or spiral) cone beam computed tomography
History
References
Notes
External links

A visual representation of the raw data obtained is called a sinogram, yet it is not sufficient for interpretation. Once the scan data has been acquired, the data must be processed using a form of tomographic reconstruction, which produces a series of cross-sectional images. In terms of mathematics, the raw data acquired by the scanner consists of multiple "projections" of the object being scanned. These projections are effectively the Radon transformation of the structure of the object. Reconstruction essentially involves solving the inverse Radon transformation.

Structure

In conventional CT machines, an X-ray tube and detector are physically rotated behind a circular shroud (see the image above right). An alternative, short lived design, known as electron beam tomography (EBT), used electromagnetic deflection of an electron beam within a very large conical X-ray tube and a stationary array of detectors to achieve very high temporal resolution, for imaging of rapidly moving structures, for example the coronary arteries. Systems with a very large number of detector rows, such that the z-axis coverage is comparable to the xy-axis coverage are often termed cone beam CT , due to the shape of the X-ray beam (strictly, the beam is pyramidal in shape, rather than conical). Cone-beam CT is commonly found in medical fluoroscopy equipment; by rotating the fluoroscope around the patient, a geometry similar to CT can be obtained, and by treating the 2D X-ray detector in a manner similar to a CT detector with a massive number of rows, it is possible to reconstruct a 3D volume from a single rotation using suitable software.

Contrast media

Contrast mediums used for X-ray CT, as well as for plain film X-ray, are called radiocontrasts. Radiocontrasts for X-ray CT are, in general, iodine-based.^[2] This is useful to highlight structures such as blood vessels that otherwise would be difficult to delineate from their surroundings. Using contrast material can also help to obtain functional information about tissues. Often, images are taken both with and without radiocontrast.

Schematic configuration and motion

In this section, the schematic configuration and motion of the parallel beam irradiation optical system configured to obtain the p(s,θ) of above-mentioned (eq. 5) will be explained. In this section, how to obtain the p(s,θ) of (eq.5) by utilizing parallel beam irradiation optical system will also be explained. Configuration and motions of parallel beam irradiation optical system, referring Fig. 3.

Statements

Numbers (1)–(7) shown in Fig. 3 (see the numbers within the parentheses) respectively indicate: (1) = an object; (2) = the parallel beam light source; (3) = the screen; (4) = transmission beam; (5) = the datum circle (a datum feature); (6) = the origin (a datum feature); and (7) = a fluoroscopic image (a one-dimensional image; p (s, θ)).

Two datum coordinate systems xy and ts are imagined in order to explain the positional relations and movements of features (0)–(7) in the figure. The xy and ts coordinate systems share the origin (6) and they are positioned on the same plane. That is, the xy plane and the ts plane are the same plane. Henceforth, this virtual plane will be called “the datum plane”. In addition, a virtual circle centered at the abovementioned origin (6) is set on the datum plane (it will be called “the datum circle” henceforth). This datum circle (5) will be represents the orbit of the parallel beam irradiation optical system. Naturally, the origin (6), the datum circle (5), and the datum coordinate systems are virtual features which are imagined for mathematical purposes.

The μ(x,y) is absorption coefficient of the object (3) at each (x,y), p(s,θ) (7) is the collection of fluoroscopic images.

Motion of parallel beam irradiation optical system

The parallel beam irradiation optical system is the key component of a CT scanner. It consists of a parallel beam X-ray source (2) and the screen (3). They are positioned so that they face each other in parallel with the origin (6) in between, both being in contact with the datum circle (6).

These two features ((2) and (3)) can rotate counterclockwise ^{[Notes 1]} around the origin (6) together with the ts coordinate system while maintaining the relative positional relations between themselves and with the ts coordinate system (so, these two features ((2) and (3)) are always opposed each other). The ts plane is positioned so that the direction from a collimated X-ray source (2) to the screen (3) matches the positive direction of the t-axis while the s-axis parallels these two features. Henceforth, the angle between the x- and the s-axes will be indicated as θ. That is, parallel beam irradiation optical system where the angle between the object and the transmission beam equals θ. This datum circle (6) will be represents the orbit of the parallel beam irradiation optical system.

On the other hand, the object (1) will be scanned by CT scanner is fixed to xy coordination system. Hence, object (1) will not be moved while the parallel beam irradiation optical system are rotated around the object (1). The object (1) must be smaller than datum circle.

Increment/Table speed

The distance the table moves for every 360° rotation of the X-ray generator is called the increment or table feed for axial scan modes. For helical scan modes, it is called table speed.^[3] Setting an increment that is smaller than the slice thickness results in overlap between the slices. A beneficial effect of this is a smoother transition between images when scrolling through the stack.^[4]

Obtaining transmission image ‘s’

During the above-mentioned motion (that is pivoting around the object(1)) of parallel beam irradiation optical system, the collimated X-ray source (2) emits transmission beam (4) which are effectively “parallel rays” in a geometrical optical sense. The traveling direction of each ray of the transmission beam (4) is parallel to the t-axis. The transmission beam (4), emitted by the X-ray source (2), penetrates the object and reaches the screen (3) after attenuation due to absorption by the object.

Optical transmission can be presumed to occur ideally. That is, transmission beam penetrates without diffraction, diffusion, or reflection although it is absorbed by the object and its attenuation is assumed to occur in accordance with the Beer-Lambert law.

Consequently, a fluoroscopic image (7) is recorded on the screen as a one-dimensional image (one image is recorded for every θ corresponding to all s values). When the angle between the object and transmission beam is θ and if the intensity of transmission beam (4) having reached each "s" point on the screen is expressed as p(s, θ), it expresses a fluoroscopic image (7) corresponding to each θ.

Tomographic reconstruction

The technique of filtered back projection is one of the most established algorithmic techniques for this problem. It is conceptually simple, tunable and deterministic. It is also computationally undemanding, with modern scanners requiring only a few milliseconds per image. However, this is not the only technique available: the original EMI scanner solved the tomographic reconstruction problem by linear algebra, but this approach was limited by its high computational complexity, especially given the computer technology available at the time. More recently, manufacturers have developed iterative physical model-based maximum likelihood expectation maximization techniques. These techniques are advantageous because they use an internal model of the scanner's physical properties and of the physical laws of X-ray interactions. Earlier methods, such as filtered back projection, assume a perfect scanner and highly simplified physics, which leads to a number of artifacts, high noise and impaired image resolution. Iterative techniques provide images with improved resolution, reduced noise and fewer artifacts, as well as the ability to greatly reduce the radiation dose in certain circumstances.^[5] The disadvantage is a very high computational requirement, but advances in computer technology and high-performance computing techniques, such as use of highly parallel GPU algorithms or use of specialized hardware such as FPGAs or ASICs, now allow practical use.

Basic principle

In this section, the basic principle of tomography in the case that especially uses tomography utilizing the parallel beam irradiation optical system will be explained.

Tomography is a technology that uses a tomographic optical system to obtain virtual 'slices' (a tomographic image) of specific cross section of a scanned object, allowing the user to see inside the object without cutting. There are several types of tomographic optical system including the parallel beam irradiation optical system. Parallel beam irradiation optical system may be the easiest and most practical example of a tomographic optical system therefore, in this article, explanation of "How to obtain the Tomographic image" will be based on "the parallel beam irradiation optical system". The resolution in tomography is typically described by the Crowther criterion.

Fig. 3 is intended to illustrate the mathematical model and to illustrate the principle of tomography. In Fig.3, absorption coefficient at a cross-sectional coordinate (x, y) of the subject is modeled as μ(x, y). Consideration based on the above assumptions may clarify the following items. Therefore, in this section, the explanation is advanced according to the order as follows:

(1)Results of measurement, i.e. a series of images obtained by transmitted light are expressed (modeled) as a function p (s,θ) obtained by performing radon transform to μ(x, y), and
(2)μ(x, y) is restored by performing inverse radon transform to measurement results.

(1) The Results of measurement of p(s,θ) in a parallel beam irradiation optical system

Consider the mathematical model where the absorption coefficient of the object at each point $(x,y)$ is represented by the function $\mu (x,y)$ and suppose that the transmission beam penetrates without diffraction, diffusion, or reflection. Also assume the beam is absorbed by the object and its attenuation occurs in accordance with the Beer-Lambert law. What we want to know then is the values of the function $\mu$ . What we can measure will be the values of the function $p(s,\theta )$ .

When the attenuation conforms to the Beer-Lambert law, the relation between ${I}_{0}$ and $I$ is given by equation ( 1 ) and the absorbance $p_{l}$ along the light beam path $l(t)$ is given by equation ( 2 ). Here ${I}_{0}$ is the intensity of the light beam before transmission, while $I$ is the beam intensity after transmission.

${\begin{aligned}I=I_{0}\exp \left({-\int \mu (x,y)\,dl}\right)=I_{0}\exp \left({-{\int }_{-\infty }^{\infty }\mu (l(t))\,|{\dot {l}}(t)|dt}\right)\end{aligned}}$

(1)

${\begin{aligned}p_{l}=\ln(I/I_{0})=-\int \mu (x,y)\,dl=-{\int }_{-\infty }^{\infty }\mu (l(t))\,|{\dot {l}}(t)|dt\end{aligned}}$

(2)

Here, the direction from the light source toward the screen is defined as the $t$ direction and that perpendicular to the $t$ direction and parallel with the screen is defined as the $s$ direction. (Both the $(t,s)$ and $(x,y)$ coordinate systems are chosen such that they are reflections of each other without mirror-reflective transformation.)^{[ clarification needed ]}

By using a parallel beam irradiation optical system, one can experimentally obtain the series of fluoroscopic images (these are one-dimensional images $p_{\theta }(s)$ of a specific cross section of a scanned object) for each angle $\theta$ between the object and the transmitted light beam. In Fig.3, the $(x,y)$ plane rotates counter clockwise. ^{[Notes 1]} around the point of origin in the plane in such a way “to keep mutual positional relationship between the light source (2) and screen (7) passing through the trajectory (5).” Rotation angle of this case is same as above-mentioned θ.

The beam having an angle $\theta$ is the collection of lines ${l}_{\theta ,s}(t)$ , represented by equation ( 3 ) below.

${l}_{\theta ,s}(t)=t{\begin{bmatrix}-\sin \theta \\\cos \theta \\\end{bmatrix}}+{\begin{bmatrix}s\cos \theta \\s\sin \theta \\\end{bmatrix}}$

(3)

The function $p_{\theta }(s)$ is defined by equation ( 4 ). That $p_{\theta }(s)$ is equal to the line integral of μ(x,y) along ${l}_{[\theta ,s]}(t)$ of (eq. 3) as the same manner of (eq.2). This means that, $p(s,\theta )$ of following (eq. 5) is a resultant of Radon transformation of μ(x,y).

$p_{\theta }(s)=-{\int }_{-\infty }^{\infty }\mu (s\cos \theta -t\sin \theta ,s\sin \theta +t\cos \theta )\,dt$

(4)

One can define following function of two variables ( 5 ). In this article, $p(s,\theta )$ is the collection of fluoroscopic images.

$p(s,\theta )=p_{\theta }(s)$

(5)

(2)μ(x, y) is restored by performing inverse radon transform to measurement results

“What we want to know (μ(x,y))” can be reconstructed from “What we measured ( p(s,θ))” by using inverse radon transformation . In the above-mentioned descriptions, “What we measured” is p(s,θ) . On the other hand, “What we want to know ” is μ(x,y). So, the next will be "How to reconstruct μ(x,y) from p(s,θ)".

Spiral CT

Spiral computed tomography, or helical computed tomography, is a computed tomography (CT) technology in which the source and detector travel along a helical path relative to the object. Typical implementations involve moving the patient couch through the bore of the scanner whilst the gantry rotates. Spiral CT can achieve improved image resolution for a given radiation dose, compared to individual slice acquisition. Most modern hospitals currently use spiral CT scanners.

Willi Kalender is credited with invention of the technique, and uses the term spiral CT.^[6] Kalender argues that the terms spiral and helical are synonymous and equally acceptable.^[7]

There are a class of image artifacts specific to helical acquisition.^[8]

Single-slice and multi-slice Spiral CT

Since its invention by Kalender in the 1980s, helical scan CT machines have steadily increased the number of rows of detectors (slices) they deploy. The prototype 16 multi-slice scanner was introduced in 2001 and in 2004, 64 multislice scanners are on the market. These can produce an image in less than a second and thus can obtain images of the heart and its blood vessels (coronary vessels) as if frozen in time.

In order to illuminate multiple rows of detector elements in a multi-slice scanner, the x-ray source must emit a beam which is divergent along the axial direction (i.e. a cone beam instead of a fan beam).

Pitch

A helical CT beam trajectory is characterized by its pitch, which is equal to the table feed distance along the scan range over one gantry rotation divided by the section collimation.^[9] When pitch is greater than 1, the radiation dose for a given axial field of view (FOV) is decreased compared to conventional CT. At high pitches there is, however, a trade-off in terms of noise and longitudinal resolution.^[10]

Helical (or spiral) cone beam computed tomography

In cone-beam computed tomography (commonly abbreviated CBCT), the X-ray beam is conical.^[11]

Helical (or spiral) cone beam computed tomography is a type of three-dimensional computed tomography (CT) in which the source (usually of X-rays) describes a helical trajectory relative to the object while a two-dimensional array of detectors measures the transmitted radiation on part of a cone of rays emanating from the source.

In practical helical cone beam X-ray CT machines, the source and array of detectors are mounted on a rotating gantry while the patient is moved axially at a uniform rate. Earlier X-ray CT scanners imaged one slice at a time by rotating source and one-dimensional array of detectors while the patient remained static. The helical scan method reduces the X-ray dose to the patient required for a given resolution while scanning more quickly. This is, however, at the cost of greater mathematical complexity in the reconstruction of the image from the measurements.

History

The earliest sensors were scintillation detectors, with photomultiplier tubes excited by (typically) cesium iodide crystals. Cesium iodide was replaced during the 1980s by ion chambers containing high-pressure xenon gas. These systems were in turn replaced by scintillation systems based on photodiodes instead of photomultipliers and modern scintillation materials (for example rare-earth garnet or rare-earth oxide ceramics) with more desirable characteristics.

Initial machines would rotate the X-ray source and detectors around a stationary object. Following a complete rotation, the object would be moved along its axis, and the next rotation started. Newer machines permitted continuous rotation with the object to be imaged slowly and smoothly slid through the X-ray ring. These are called helical or spiral CT machines. A subsequent development of helical CT was multi-slice (or multi-detector) CT; instead of a single row of detectors, multiple rows of detectors are used effectively capturing multiple cross-sections simultaneously.

Related Research Articles

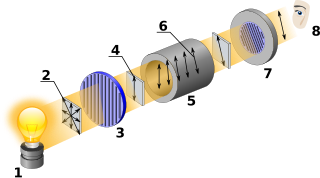
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes or metamaterials.

A computed tomography scan is a medical imaging technique used to obtain detailed internal images of the body. The personnel that perform CT scans are called radiographers or radiology technologists.

Medical imaging is the technique and process of imaging the interior of a body for clinical analysis and medical intervention, as well as visual representation of the function of some organs or tissues (physiology). Medical imaging seeks to reveal internal structures hidden by the skin and bones, as well as to diagnose and treat disease. Medical imaging also establishes a database of normal anatomy and physiology to make it possible to identify abnormalities. Although imaging of removed organs and tissues can be performed for medical reasons, such procedures are usually considered part of pathology instead of medical imaging.

<span class="mw-page-title-main">Single-photon emission computed tomography</span> Nuclear medicine tomographic imaging technique

Single-photon emission computed tomography is a nuclear medicine tomographic imaging technique using gamma rays. It is very similar to conventional nuclear medicine planar imaging using a gamma camera, but is able to provide true 3D information. This information is typically presented as cross-sectional slices through the patient, but can be freely reformatted or manipulated as required.

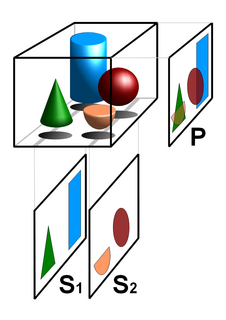
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, astrophysics, quantum information, and other areas of science. The word tomography is derived from Ancient Greek τόμος tomos, "slice, section" and γράφω graphō, "to write" or, in this context as well, "to describe." A device used in tomography is called a tomograph, while the image produced is a tomogram.

Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of rays. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances.

Technicare, formerly known as Ohio Nuclear, made CT, DR and MRI scanners and other medical imaging equipment. Its headquarters was in Solon, Ohio. Originally an independent company which became publicly traded, it was later purchased by Johnson & Johnson. At the time, Invacare was also owned by Technicare. A Harvard Business Case was written about the challenges that precipitated the transition. The company did not do well under Johnson & Johnson and in 1986, under economic pressure following unrelated losses from two Tylenol product tampering cases, J&J folded the company, selling the intellectual property and profitable service business to General Electric, a competitor.

Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.

<span class="mw-page-title-main">X-ray microtomography</span>

X-ray microtomography, like tomography and X-ray computed tomography, uses X-rays to create cross-sections of a physical object that can be used to recreate a virtual model without destroying the original object. The prefix micro- is used to indicate that the pixel sizes of the cross-sections are in the micrometre range. These pixel sizes have also resulted in the terms high-resolution X-ray tomography, micro–computed tomography, and similar terms. Sometimes the terms high-resolution CT (HRCT) and micro-CT are differentiated, but in other cases the term high-resolution micro-CT is used. Virtually all tomography today is computed tomography.

Computed tomography laser mammography (CTLM) is the trademark of Imaging Diagnostic Systems, Inc. for its optical tomographic technique for female breast imaging.

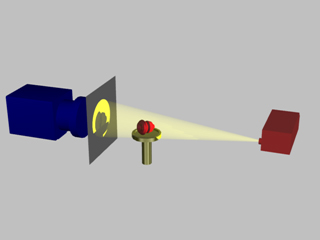
<span class="mw-page-title-main">Cone beam reconstruction</span>

In microtomography X-ray scanners, cone beam reconstruction is one of two common scanning methods, the other being Fan beam reconstruction.

An X-ray microscope uses electromagnetic radiation in the soft X-ray band to produce images of very small objects.

<span class="mw-page-title-main">Monte Carlo method for photon transport</span>

Modeling photon propagation with Monte Carlo methods is a flexible yet rigorous approach to simulate photon transport. In the method, local rules of photon transport are expressed as probability distributions which describe the step size of photon movement between sites of photon-matter interaction and the angles of deflection in a photon's trajectory when a scattering event occurs. This is equivalent to modeling photon transport analytically by the radiative transfer equation (RTE), which describes the motion of photons using a differential equation. However, closed-form solutions of the RTE are often not possible; for some geometries, the diffusion approximation can be used to simplify the RTE, although this, in turn, introduces many inaccuracies, especially near sources and boundaries. In contrast, Monte Carlo simulations can be made arbitrarily accurate by increasing the number of photons traced. For example, see the movie, where a Monte Carlo simulation of a pencil beam incident on a semi-infinite medium models both the initial ballistic photon flow and the later diffuse propagation.

The computed tomography dose index (CTDI) is a commonly used radiation exposure index in X-ray computed tomography (CT), first defined in 1981. The unit of CTDI is the gray (Gy) and it can be used in conjunction with patient size to estimate the absorbed dose. The CTDI and absorbed dose may differ by more than a factor of two for small patients such as children.

Industrial computed tomography (CT) scanning is any computer-aided tomographic process, usually X-ray computed tomography, that uses irradiation to produce three-dimensional internal and external representations of a scanned object. Industrial CT scanning has been used in many areas of industry for internal inspection of components. Some of the key uses for industrial CT scanning have been flaw detection, failure analysis, metrology, assembly analysis and reverse engineering applications. Just as in medical imaging, industrial imaging includes both nontomographic radiography and computed tomographic radiography.

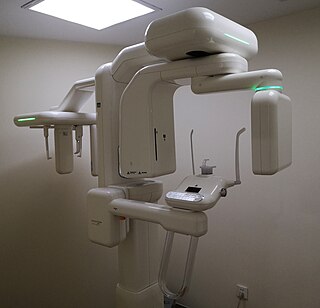
Cone beam computed tomography is a medical imaging technique consisting of X-ray computed tomography where the X-rays are divergent, forming a cone.

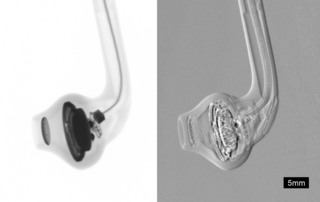
<span class="mw-page-title-main">Phase-contrast X-ray imaging</span> Imaging systems using changes in phase

Phase-contrast X-ray imaging or phase-sensitive X-ray imaging is a general term for different technical methods that use information concerning changes in the phase of an X-ray beam that passes through an object in order to create its images. Standard X-ray imaging techniques like radiography or computed tomography (CT) rely on a decrease of the X-ray beam's intensity (attenuation) when traversing the sample, which can be measured directly with the assistance of an X-ray detector. However, in phase contrast X-ray imaging, the beam's phase shift caused by the sample is not measured directly, but is transformed into variations in intensity, which then can be recorded by the detector.

The problem of reconstructing a multidimensional signal from its projection is uniquely multidimensional, having no 1-D counterpart. It has applications that range from computer-aided tomography to geophysical signal processing. It is a problem which can be explored from several points of view—as a deconvolution problem, a modeling problem, an estimation problem, or an interpolation problem.

Photon-counting computed tomography (PCCT) is a form of X-ray computed tomography (CT) in which X-rays are detected using a photon-counting detector (PCD) which registers the interactions of individual photons. By keeping track of the deposited energy in each interaction, the detector pixels of a PCD each record an approximate energy spectrum, making it a spectral or energy-resolved CT technique. In contrast, more conventional CT scanners use energy-integrating detectors (EIDs), where the total energy deposited in a pixel during a fixed period of time is registered. These EIDs thus register only photon intensity, comparable to black-and-white photography, whereas PCDs register also spectral information, similar to color photography.

<span class="mw-page-title-main">History of computed tomography</span> History of CT scanning technology

The history of X-ray computed tomography dates back to at least 1917 with the mathematical theory of the Radon transform In October 1963, William H. Oldendorf received a U.S. patent for a "radiant energy apparatus for investigating selected areas of interior objects obscured by dense material". The first clinical CT scan was performed in 1971 using a scanner invented by Sir Godfrey Hounsfield.

References

↑ Jun, Kyungtaek; Yoon, Seokhwan (2017). "Alignment Solution for CT Image Reconstruction using Fixed Point and Virtual Rotation Axis". Scientific Reports. 7: 41218. arXiv: 1605.04833 . Bibcode:2017NatSR...741218J. doi:10.1038/srep41218. ISSN 2045-2322. PMC 5264594 . PMID 28120881.
↑ Webb, W. Richard; Brant, Wiliam E.; Major, Nancy M. (2014). Fundamentals of Body CT. Elsevier Health Sciences. p. 152. ISBN 9780323263580.
↑ "CT scan parameters: Translation of terms for different manufacturers" (PDF). IAEA . American Association of Physicists in Medicine. 2011-08-11.
↑ Page 310 in: Kristen M. Waterstram-Rich; David Gilmore (2016). Nuclear Medicine and PET/CT: Technology and Techniques (8 ed.). Elsevier Health Sciences. ISBN 9780323400350.
↑ Barkan, O; Weill, J; Averbuch, A; Dekel, S. "Adaptive Compressed Tomography Sensing". In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2013 (pp. 2195–2202).
↑ Kalender WA (1994). "Technical foundations of spiral CT" Semin Ultrasound CT MR 15: (2) 81-89.
↑ Kalender WA (1994). "Spiral or helical CT: right or wrong?" Radiology Archived 2010-10-11 at the Wayback Machine 193: (2) 583.
↑ Barrett and Keat (2004) RadioGraphics 24:1679-1691 https://dx.doi.org/10.1148/rg.246045065
↑ Heiken et al. (1993) Radiology 189:647-656 https://dx.doi.org/10.1148/radiology.189.3.8234684
↑ Maldjian and Goldman (2013) AJR 200:741-747 https://dx.doi.org/10.2214/AJR.12.9768
↑ Helical+Cone-Beam+CT at the US National Library of Medicine Medical Subject Headings (MeSH)

Notes

1 2 In this article, the following discussion is developed based on anticlockwise motion. But, whether the direction of the rotation is anti-clockwise or a clockwise is not an essential problem. Even if the rotational direction is assumed to be in an opposite direction, no specific impact is caused on essential level except for some minor deformation of formula including reversing a part of positive or negative signs.

External links

Principles of Computerized Tomographic Imaging

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Jun, Kyungtaek; Yoon, Seokhwan (2017). "Alignment Solution for CT Image Reconstruction using Fixed Point and Virtual Rotation Axis". Scientific Reports. 7: 41218. arXiv: 1605.04833 . Bibcode:2017NatSR...741218J. doi:10.1038/srep41218. ISSN 2045-2322. PMC 5264594 . PMID 28120881.

[2] Webb, W. Richard; Brant, Wiliam E.; Major, Nancy M. (2014). Fundamentals of Body CT. Elsevier Health Sciences. p. 152. ISBN 9780323263580.

[4] "CT scan parameters: Translation of terms for different manufacturers" (PDF). IAEA . American Association of Physicists in Medicine. 2011-08-11.

[5] Page 310 in: Kristen M. Waterstram-Rich; David Gilmore (2016). Nuclear Medicine and PET/CT: Technology and Techniques (8 ed.). Elsevier Health Sciences. ISBN 9780323400350.

[ata-6] Barkan, O; Weill, J; Averbuch, A; Dekel, S. "Adaptive Compressed Tomography Sensing". In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2013 (pp. 2195–2202).

[7] Kalender WA (1994). "Technical foundations of spiral CT" Semin Ultrasound CT MR 15: (2) 81-89.

[8] Kalender WA (1994). "Spiral or helical CT: right or wrong?" Radiology Archived 2010-10-11 at the Wayback Machine 193: (2) 583.

[9] Barrett and Keat (2004) RadioGraphics 24:1679-1691 https://dx.doi.org/10.1148/rg.246045065

[10] Heiken et al. (1993) Radiology 189:647-656 https://dx.doi.org/10.1148/radiology.189.3.8234684

[11] Maldjian and Goldman (2013) AJR 200:741-747 https://dx.doi.org/10.2214/AJR.12.9768

[12] Helical+Cone-Beam+CT at the US National Library of Medicine Medical Subject Headings (MeSH)

[n1-3] 1 2 In this article, the following discussion is developed based on anticlockwise motion. But, whether the direction of the rotation is anti-clockwise or a clockwise is not an essential problem. Even if the rotational direction is assumed to be in an opposite direction, no specific impact is caused on essential level except for some minor deformation of formula including reversing a part of positive or negative signs.

[2]

[Notes 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]