First-order logic—also called predicate logic, predicate calculus, quantificational logic—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables. Rather than propositions such as "all men are mortal", in first-order logic one can have expressions in the form "for all x, if x is a man, then x is mortal"; where "for all x" is a quantifier, x is a variable, and "... is a man" and "... is mortal" are predicates. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.

The proof of Gödel's completeness theorem given by Kurt Gödel in his doctoral dissertation of 1929 is not easy to read today; it uses concepts and formalisms that are no longer used and terminology that is often obscure. The version given below attempts to represent all the steps in the proof and all the important ideas faithfully, while restating the proof in the modern language of mathematical logic. This outline should not be considered a rigorous proof of the theorem.
In mathematical logic, a universal quantification is a type of quantifier, a logical constant which is interpreted as "given any", "for all", or "for any". It expresses that a predicate can be satisfied by every member of a domain of discourse. In other words, it is the predication of a property or relation to every member of the domain. It asserts that a predicate within the scope of a universal quantifier is true of every value of a predicate variable.
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a variable may be said to be either free or bound. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. A free variable is a notation (symbol) that specifies places in an expression where substitution may take place and is not a parameter of this or any container expression. The idea is related to a placeholder, or a wildcard character that stands for an unspecified symbol.
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.
A formula of the predicate calculus is in prenex normal form (PNF) if it is written as a string of quantifiers and bound variables, called the prefix, followed by a quantifier-free part, called the matrix. Together with the normal forms in propositional logic, it provides a canonical normal form useful in automated theorem proving.
In mathematical logic, a formula of first-order logic is in Skolem normal form if it is in prenex normal form with only universal first-order quantifiers.

Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book.
In logic and analytic philosophy, an atomic sentence is a type of declarative sentence which is either true or false and which cannot be broken down into other simpler sentences. For example, "The dog ran" is an atomic sentence in natural language, whereas "The dog ran and the cat hid" is a molecular sentence in natural language.
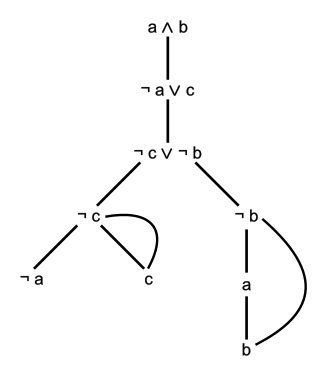
In proof theory, the semantic tableau, also called an analytic tableau, truth tree, or simply tree, is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.
In mathematical logic, a propositional variable is an input variable of a truth function. Propositional variables are the basic building-blocks of propositional formulas, used in propositional logic and higher-order logics.
Independence-friendly logic is an extension of classical first-order logic (FOL) by means of slashed quantifiers of the form and , where is a finite set of variables. The intended reading of is "there is a which is functionally independent from the variables in ". IF logic allows one to express more general patterns of dependence between variables than those which are implicit in first-order logic. This greater level of generality leads to an actual increase in expressive power; the set of IF sentences can characterize the same classes of structures as existential second-order logic.
In mathematical logic, a sentence of a predicate logic is a Boolean-valued well-formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that must be true or false. The restriction of having no free variables is needed to make sure that sentences can have concrete, fixed truth values: as the free variables of a (general) formula can range over several values, the truth value of such a formula may vary.
Circumscription is a non-monotonic logic created by John McCarthy to formalize the common sense assumption that things are as expected unless otherwise specified. Circumscription was later used by McCarthy in an attempt to solve the frame problem. To implement circumscription in its initial formulation, McCarthy augmented first-order logic to allow the minimization of the extension of some predicates, where the extension of a predicate is the set of tuples of values the predicate is true on. This minimization is similar to the closed-world assumption that what is not known to be true is false.
In mathematical logic, a tautology is a formula that is true regardless of the interpretation of its component terms, with only the logical constants having a fixed meaning. For example, a formula that states, "the ball is green or the ball is not green," is always true, regardless of what a ball is and regardless of its colour. Tautology is usually, though not always, used to refer to valid formulas of propositional logic.
In logic, the monadic predicate calculus is the fragment of first-order logic in which all relation symbols in the signature are monadic, and there are no function symbols. All atomic formulas are thus of the form , where is a relation symbol and is a variable.
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier in the first order formula expresses that everything in the domain satisfies the property denoted by . On the other hand, the existential quantifier in the formula expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable.
In mathematical logic, the spectrum of a sentence is the set of natural numbers occurring as the size of a finite model in which a given sentence is true. By a result in descriptive complexity, a set of natural numbers is a spectrum if and only if it can be recognized in non-deterministic exponential time.
In mathematical logic, fixed-point logics are extensions of classical predicate logic that have been introduced to express recursion. Their development has been motivated by descriptive complexity theory and their relationship to database query languages, in particular to Datalog.





