In Western musical notation, a key signature is a set of sharp, flat, or rarely, natural symbols placed on the staff at the beginning of a section of music. The initial key signature in a piece is placed immediately after the clef at the beginning of the first line. If the piece contains a section in a different key, the new key signature is placed at the beginning of that section.
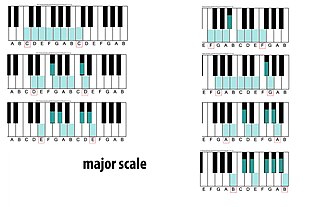
The major scale is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at double its frequency so that it is called a higher octave of the same note.
In music, an octave or perfect octave is a series of eight notes occupying the interval between two notes, one having twice the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave have the same name and are of the same pitch class.
In musical notation, an accidental is a symbol that indicates an alteration of a given pitch. The most common accidentals are the flat and the sharp, which represent alterations of a semitone, and the natural, which cancels a sharp or flat. Accidentals alter the pitch of individual scale tones in a given key signature; the sharps or flats in the key signature itself are not considered accidentals.
C or Do is the first note of the C major scale, the third note of the A minor scale, and the fourth note of the Guidonian hand, commonly pitched around 261.63 Hz. The actual frequency has depended on historical pitch standards, and for transposing instruments a distinction is made between written and sounding or concert pitch. It has enharmonic equivalents of B♯ and D.
In music, two written notes have enharmonic equivalence if they produce the same pitch but are notated differently. Similarly, written intervals, chords, or key signatures are considered enharmonic if they represent identical pitches that are notated differently. The term derives from Latin enharmonicus, in turn from Late Latin enarmonius, from Ancient Greek ἐναρμόνιος, from ἐν ('in') and ἁρμονία ('harmony').
In music, sharp – eqv. dièse or diesis – means higher in pitch. The sharp symbol, ♯, indicates that the note to which the symbol is applied is played one semitone higher. The opposite of sharp is flat, indicating a lowering of pitch. The ♯ symbol derives from a square form of the letter b.

In music theory, the circle of fifths is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music, the sequence is: C, G, D, A, E, B, F♯/G♭, C♯/D♭, G♯/A♭, D♯/E♭, A♯/B♭, F, and C. This order places the most closely related key signatures adjacent to one another.
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave position." Important to musical set theory, a pitch class is "all pitches related to each other by octave, enharmonic equivalence, or both." Thus, using scientific pitch notation, the pitch class "C" is the set

In music, letter notation is a system of representing a set of pitches, for example, the notes of a scale, by letters. For the complete Western diatonic scale, for example, these would be the letters A-G, possibly with a trailing symbol to indicate a half-step raise or a half-step lowering. This is the most common way of specifying a note in speech or in written text in English or German. In Germany, Scandinavia, and parts of Central and Eastern Europe, H is used instead of B, and B is used instead of B♭. In traditional Irish music, where almost all tunes are restricted to two octaves, notes in the lower octave are written in lower case while those in the upper octave are written in upper case.

Scientific pitch notation (SPN), also known as American standard pitch notation (ASPN) and international pitch notation (IPN), is a method of specifying musical pitch by combining a musical note name and a number identifying the pitch's octave.
This is a list of the fundamental frequencies in hertz (cycles per second) of the keys of a modern 88-key standard or 108-key extended piano in twelve-tone equal temperament, with the 49th key, the fifth A (called A4), tuned to 440 Hz (referred to as A440). Every octave is made of twelve steps called semitones. A jump from the lowest semitone to the highest semitone in one octave doubles the frequency (for example, the fifth A is 440 Hz and the sixth A is 880 Hz). The frequency of a pitch is derived by multiplying (ascending) or dividing (descending) the frequency of the previous pitch by the twelfth root of two (approximately 1.059463). For example, to get the frequency one semitone up from A4 (A♯4), multiply 440 Hz by the twelfth root of two. To go from A4 up two semitones (one whole tone) to B4, multiply 440 twice by the twelfth root of two (or once by the sixth root of two, approximately 1.122462). To go from A4 up three semitones to C5 (a minor third), multiply 440 Hz three times by the twelfth root of two (or once by the fourth root of two, approximately 1.189207). For other tuning schemes, refer to musical tuning.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Traditionally, there are two most common comma; the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
A is a musical note equivalent to 440 Hz in typical A440 tuning. It is the sixth note of La and the tenth semitone of the fixed-do solfège.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21 ∕ 53 , or 22.6415 cents, an interval sometimes called the Holdrian comma.
MIDI Tuning Standard (MTS) is a specification of precise musical pitch agreed to by the MIDI Manufacturers Association in the MIDI protocol. MTS allows for both a bulk tuning dump message, giving a tuning for each of 128 notes, and a tuning message for individual notes as they are played.
E is the third note and the fifth semitone of the C major scale, and mi in fixed-do solfège. It has enharmonic equivalents of F♭ [(F-flat) which is by definition a diatonic semitone above E♭] and D, amongst others.

F♯ is the seventh semitone of the solfège.
C♯ (C-sharp) is a musical note lying a chromatic semitone above C and a diatonic semitone below D; it is the second semitone of the solfège. C-sharp is thus enharmonic to D♭. It is the second semitone in the French solfège and is known there as do dièse. In some European notations, it is known as Cis. In equal temperament it is also enharmonic with B.

B♭ (B-flat), or, in some European countries, B, is the eleventh step of the Western chromatic scale. It lies a diatonic semitone above A and a chromatic semitone below B, thus being enharmonic to A♯, even though in some musical tunings, B♭ will have a different sounding pitch than A♯. B-flat is also enharmonic to C.








![Logarithmic plot of frequency in hertz versus pitch of a chromatic scale starting on middle C. Each subsequent note has a pitch equal to the frequency of the prior note's pitch multiplied by [?]2. Frequency vs name.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/6/65/Frequency_vs_name.svg/228px-Frequency_vs_name.svg.png)

















