In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.

Chaos theory is a branch of mathematics focusing on the study of chaos — dynamical systems whose apparently random states of disorder and irregularities are actually governed by underlying patterns and deterministic laws that are highly sensitive to initial conditions. Chaos theory is an interdisciplinary theory stating that, within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnectedness, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Texas can cause a hurricane in China.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written

In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

In fluid dynamics, a vortex is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil.

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.

In fluid dynamics, the Taylor–Couette flow consists of a viscous fluid confined in the gap between two rotating cylinders. For low angular velocities, measured by the Reynolds number Re, the flow is steady and purely azimuthal. This basic state is known as circular Couette flow, after Maurice Marie Alfred Couette, who used this experimental device as a means to measure viscosity. Sir Geoffrey Ingram Taylor investigated the stability of Couette flow in a ground-breaking paper. Taylor's paper became a cornerstone in the development of hydrodynamic stability theory and demonstrated that the no-slip condition, which was in dispute by the scientific community at the time, was the correct boundary condition for viscous flows at a solid boundary.

Chua's circuit is a simple electronic circuit that exhibits classic chaotic behavior. This means roughly that it is a "nonperiodic oscillator"; it produces an oscillating waveform that, unlike an ordinary electronic oscillator, never "repeats". It was invented in 1983 by Leon O. Chua, who was a visitor at Waseda University in Japan at that time. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system, leading some to declare it "a paradigm for chaos".
In dynamical systems theory, a period-doubling bifurcation occurs when a slight change in a system's parameters causes a new periodic trajectory to emerge from an existing periodic trajectory—the new one having double the period of the original. With the doubled period, it takes twice as long for the numerical values visited by the system to repeat themselves.

In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics, or different forms of chaotic dynamics.

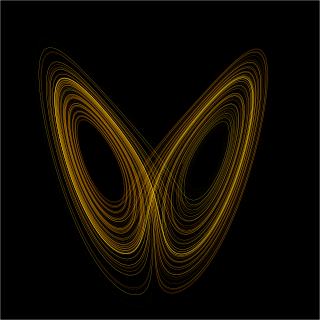
The Lorenz system is a system of ordinary differential equations first studied by Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, i.e. that in any physical system, in the absence of perfect knowledge of the initial conditions, our ability to predict its future course will always fail. This underscores that physical systems can be completely deterministic and yet still be inherently unpredictable even in the absence of quantum effects. The shape of the Lorenz attractor itself, when plotted graphically, may also be seen to resemble a butterfly.
In lab experiments that study chaos theory, approaches designed to control chaos are based on certain observed system behaviors. Any chaotic attractor contains an infinite number of unstable, periodic orbits. Chaotic dynamics, then, consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different unstable, periodic orbit where it remains for a limited time, and so forth. This results in a complicated and unpredictable wandering over longer periods of time.

The standard map is an area-preserving chaotic map from a square with side onto itself. It is constructed by a Poincaré's surface of section of the kicked rotator, and is defined by:
Synchronization of chaos is a phenomenon that may occur when two, or more, dissipative chaotic systems are coupled.
A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases.
In physics, the history of centrifugal and centripetal forces illustrates a long and complex evolution of thought about the nature of forces, relativity, and the nature of physical laws.

Stellar pulsations are caused by expansions and contractions in the outer layers as a star seeks to maintain equilibrium. These fluctuations in stellar radius cause corresponding changes in the luminosity of the star. Astronomers are able to deduce this mechanism by measuring the spectrum and observing the Doppler effect. Many intrinsic variable stars that pulsate with large amplitudes, such as the classical Cepheids, RR Lyrae stars and large-amplitude Delta Scuti stars show regular light curves.
![Plots of the trajectories of the centers of mass of the above two wheels, left and right respectively, after the same extended period of time. In each plot, the center of mass
M
[?]
R
2
{\displaystyle M\in \mathbb {R} ^{2}}
is the vector
(
M
x
,
M
y
)
T
{\displaystyle (M_{x},M_{y})^{T}}
, where
M
x
{\displaystyle M_{x}}
and
M
y
{\displaystyle M_{y}}
are the
x
{\displaystyle x}
and
y
{\displaystyle y}
components, respectively. The system indeed appears to exhibit a great dependence on initial conditions, a defining property of chaotic systems; moreover, two attractors of the system are seen in both plots. Plots of centers of mass of two Malkus waterwheels with slightly varied initial condition.jpg](http://upload.wikimedia.org/wikipedia/commons/thumb/0/0f/Plots_of_centers_of_mass_of_two_Malkus_waterwheels_with_slightly_varied_initial_condition.jpg/627px-Plots_of_centers_of_mass_of_two_Malkus_waterwheels_with_slightly_varied_initial_condition.jpg)
















