Magnitude (mathematics)

Last updated

In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an ordering (or ranking) of the class of objects to which it belongs. Magnitude as a concept dates to Ancient Greece and has been applied as a measure of distance from one object to another. For numbers, the absolute value of a number is commonly applied as the measure of units between a number and zero.

Contents

In vector spaces, the Euclidean norm is a measure of magnitude used to define a distance between two points in space. In physics, magnitude can be defined as quantity or distance. An order of magnitude is typically defined as a unit of distance between one number and another's numerical places on the decimal scale.

History

Ancient Greeks distinguished between several types of magnitude, [1] including:

They proved that the first two could not be the same, or even isomorphic systems of magnitude. [2] They did not consider negative magnitudes to be meaningful, and magnitude is still primarily used in contexts in which zero is either the smallest size or less than all possible sizes.

Numbers

The magnitude of any number is usually called its absolute value or modulus, denoted by . [3]

Real numbers

The absolute value of a real number r is defined by: [4]

Absolute value may also be thought of as the number's distance from zero on the real number line. For example, the absolute value of both 70 and −70 is 70.

Complex numbers

A complex number z may be viewed as the position of a point P in a 2-dimensional space, called the complex plane. The absolute value (or modulus ) of z may be thought of as the distance of P from the origin of that space. The formula for the absolute value of z = a + bi is similar to that for the Euclidean norm of a vector in a 2-dimensional Euclidean space: [5]

where the real numbers a and b are the real part and the imaginary part of z, respectively. For instance, the modulus of −3 + 4i is . Alternatively, the magnitude of a complex number z may be defined as the square root of the product of itself and its complex conjugate, , where for any complex number , its complex conjugate is .

(where ).

Vector spaces

Euclidean vector space

A Euclidean vector represents the position of a point P in a Euclidean space. Geometrically, it can be described as an arrow from the origin of the space (vector tail) to that point (vector tip). Mathematically, a vector x in an n-dimensional Euclidean space can be defined as an ordered list of n real numbers (the Cartesian coordinates of P): x = [x1, x2, ..., xn]. Its magnitude or length, denoted by , [6] is most commonly defined as its Euclidean norm (or Euclidean length): [7]

For instance, in a 3-dimensional space, the magnitude of [3, 4, 12] is 13 because This is equivalent to the square root of the dot product of the vector with itself:

The Euclidean norm of a vector is just a special case of Euclidean distance: the distance between its tail and its tip. Two similar notations are used for the Euclidean norm of a vector x:

A disadvantage of the second notation is that it can also be used to denote the absolute value of scalars and the determinants of matrices, which introduces an element of ambiguity.

Normed vector spaces

By definition, all Euclidean vectors have a magnitude (see above). However, a vector in an abstract vector space does not possess a magnitude.

A vector space endowed with a norm, such as the Euclidean space, is called a normed vector space. [8] The norm of a vector v in a normed vector space can be considered to be the magnitude of v.

Pseudo-Euclidean space

In a pseudo-Euclidean space, the magnitude of a vector is the value of the quadratic form for that vector.

Logarithmic magnitudes

When comparing magnitudes, a logarithmic scale is often used. Examples include the loudness of a sound (measured in decibels), the brightness of a star, and the Richter scale of earthquake intensity. Logarithmic magnitudes can be negative. In the natural sciences, a logarithmic magnitude is typically referred to as a level .

Order of magnitude

Orders of magnitude denote differences in numeric quantities, usually measurements, by a factor of 10—that is, a difference of one digit in the location of the decimal point.

Other mathematical measures

This section is an excerpt from Measure (mathematics).[ edit ]
Informally, a measure has the property of being monotone in the sense that if A {\displaystyle A} is a subset of B , {\displaystyle B,} the measure of A {\displaystyle A} is less than or equal to the measure of B . {\displaystyle B.} Furthermore, the measure of the empty set is required to be 0. A simple example is a volume (how big an object occupies a space) as a measure. Measure illustration (Vector).svg
Informally, a measure has the property of being monotone in the sense that if is a subset of the measure of is less than or equal to the measure of Furthermore, the measure of the empty set is required to be 0. A simple example is a volume (how big an object occupies a space) as a measure.

In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as magnitude, mass, and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general.

The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. [9] [10] But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Constantin Carathéodory, and Maurice Fréchet, among others.

See also

Related Research Articles

<span class="mw-page-title-main">Absolute value</span> Distance from zero to a number

In mathematics, the absolute value or modulus of a real number , denoted , is the non-negative value of without regard to its sign. Namely, if is a positive number, and if is negative, and . For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero.

In mathematics, more specifically in ring theory, a Euclidean domain is an integral domain that can be endowed with a Euclidean function which allows a suitable generalization of Euclidean division of integers. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them. In particular, the existence of efficient algorithms for Euclidean division of integers and of polynomials in one variable over a field is of basic importance in computer algebra.

<span class="mw-page-title-main">Normed vector space</span> Vector space on which a distance is defined

In mathematics, a normed vector space or normed space is a vector space over the real or complex numbers on which a norm is defined. A norm is a generalization of the intuitive notion of "length" in the physical world. If is a vector space over , where is a field equal to or to , then a norm on is a map , typically denoted by , satisfying the following four axioms:

  1. Non-negativity: for every ,.
  2. Positive definiteness: for every , if and only if is the zero vector.
  3. Absolute homogeneity: for every and ,
  4. Triangle inequality: for every and ,
<span class="mw-page-title-main">Euclidean vector</span> Geometric object that has length and direction

In mathematics, physics, and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Euclidean vectors can be added and scaled to form a vector space. A vector quantity is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a directed line segment. A vector is frequently depicted graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by

<span class="mw-page-title-main">Distance</span> Separation between two points

Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria. The term is also frequently used metaphorically to mean a measurement of the amount of difference between two similar objects or a degree of separation. Most such notions of distance, both physical and metaphorical, are formalized in mathematics using the notion of a metric space.

<span class="mw-page-title-main">Quaternion</span> Noncommutative extension of the complex numbers

In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by H, or in blackboard bold by Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form

<span class="mw-page-title-main">Euclidean distance</span> Length of a line segment

In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance.

<span class="mw-page-title-main">Triangle inequality</span> Property of geometry, also used to generalize the notion of "distance" in metric spaces

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If a, b, and c are the lengths of the sides of a triangle then the triangle inequality states that

<span class="mw-page-title-main">Curvature</span> Mathematical measure of how much a curve or surface deviates from flatness

In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers, and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space.

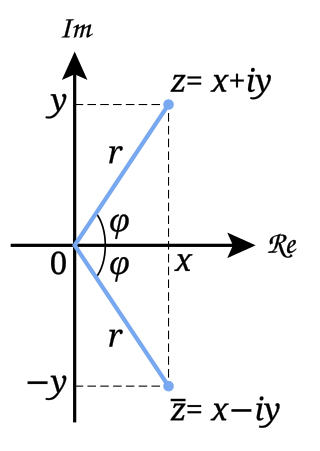
<span class="mw-page-title-main">Complex conjugate</span> Fundamental operation on complex numbers

In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if and are real numbers, then the complex conjugate of is The complex conjugate of is often denoted as or .

<span class="mw-page-title-main">Taxicab geometry</span> Type of metric geometry

Taxicab geometry or Manhattan geometry is geometry where the familiar Euclidean distance is ignored, and the distance between two points is instead defined to be the sum of the absolute differences of their respective Cartesian coordinates, a distance function called the taxicab distance, Manhattan distance, or city block distance. The name refers to the island of Manhattan, or generically any planned city with a rectangular grid of streets, in which a taxicab can only travel along grid directions. In taxicab geometry, the distance between any two points equals the length of their shortest grid path. This different definition of distance also leads to a different definition of the length of a curve, for which a line segment between any two points has the same length as a grid path between those points rather than its Euclidean length.

In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself.

<span class="mw-page-title-main">Real coordinate space</span> Space formed by the n-tuples of real numbers

In mathematics, the real coordinate space or real coordinate n-space, of dimension n, denoted Rn or , is the set of all ordered n-tuples of real numbers, that is the set of all sequences of n real numbers, also known as coordinate vectors. Special cases are called the real lineR1, the real coordinate planeR2, and the real coordinate three-dimensional spaceR3. With component-wise addition and scalar multiplication, it is a real vector space.

<span class="mw-page-title-main">Three-dimensional space</span> Geometric model of the physical space

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called 3-manifolds. The term may also refer colloquially to a subset of space, a three-dimensional region, a solid figure.

In data analysis, cosine similarity is a measure of similarity between two non-zero vectors defined in an inner product space. Cosine similarity is the cosine of the angle between the vectors; that is, it is the dot product of the vectors divided by the product of their lengths. It follows that the cosine similarity does not depend on the magnitudes of the vectors, but only on their angle. The cosine similarity always belongs to the interval For example, two proportional vectors have a cosine similarity of 1, two orthogonal vectors have a similarity of 0, and two opposite vectors have a similarity of -1. In some contexts, the component values of the vectors cannot be negative, in which case the cosine similarity is bounded in .

In functional analysis, the dual norm is a measure of size for a continuous linear function defined on a normed vector space.

<span class="mw-page-title-main">Hilbert space</span> Type of topological vector space


In mathematics, a Hilbert space generalizes the notion of Euclidean space. It extends the methods of linear algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is a vector space equipped with an inner product operation, which allows lengths and angles to be defined. Furthermore, Hilbert spaces are complete, which means that there are enough limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space.

Six-dimensional space is any space that has six dimensions, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the environment. Of particular interest is six-dimensional Euclidean space, in which 6-polytopes and the 5-sphere are constructed. Six-dimensional elliptical space and hyperbolic spaces are also studied, with constant positive and negative curvature.

In mathematics, an algebraic number field is an extension field of the field of rational numbers such that the field extension has finite degree . Thus is a field that contains and has finite dimension when considered as a vector space over .

References

  1. ↑ Heath, Thomas Smd. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.
  2. ↑ Bloch, Ethan D. (2011), The Real Numbers and Real Analysis, Springer, p. 52, ISBN   9780387721774 – via Google Books, The idea of incommensurable pairs of lengths of line segments was discovered in ancient Greece.
  3. ↑ "Magnitude Definition (Illustrated Mathematics Dictionary)". mathsisfun.com. Retrieved 2020-08-23.
  4. ↑ Mendelson, Elliott (2008). Schaum's Outline of Beginning Calculus. McGraw-Hill Professional. p. 2. ISBN   978-0-07-148754-2.
  5. ↑ Ahlfors, Lars V. (1953). Complex Analysis . Tokyo: McGraw Hill Kogakusha.
  6. ↑ Nykamp, Duane. "Magnitude of a vector definition". Math Insight. Retrieved August 23, 2020.
  7. ↑ Howard Anton; Chris Rorres (12 April 2010). Elementary Linear Algebra: Applications Version. John Wiley & Sons. ISBN   978-0-470-43205-1 – via Google Books.
  8. ↑ Golan, Johnathan S. (January 2007), The Linear Algebra a Beginning Graduate Student Ought to Know (2nd ed.), Springer, ISBN   978-1-4020-5494-5
  9. ↑ Archimedes Measuring the Circle
  10. ↑ Heath, T. L. (1897). "Measurement of a Circle". The Works Of Archimedes. Osmania University, Digital Library Of India. Cambridge University Press. pp. 91–98.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.