Glueball

Last updated

In particle physics, a glueball (also gluonium, gluon-ball) is a hypothetical composite particle. [1] It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction between themselves. Glueballs are extremely difficult to identify in particle accelerators, because they mix with ordinary meson states. [2] [3] In pure gauge theory, glueballs are the only states of the spectrum and some of them are stable. [4]

Contents

Theoretical calculations show that glueballs should exist at energy ranges accessible with current collider technology. However, due to the aforementioned difficulty (among others), they have so far not been observed and identified with certainty, [5] although phenomenological calculations have suggested that an experimentally identified glueball candidate, denoted , has properties consistent with those expected of a Standard Model glueball. [6]

The prediction that glueballs exist is one of the most important predictions of the Standard Model of particle physics that has not yet been confirmed experimentally. [7] [ failed verification ] Glueballs are the only particles predicted by the Standard Model with total angular momentum (J) (sometimes called "intrinsic spin") that could be either 2 or 3 in their ground states.

Experimental evidence was announced in 2021, by the TOTEM collaboration at the LHC in collaboration with the DØ collaboration at the former Tevatron collider at Fermilab, of odderon (a composite gluonic particle with odd C-parity) exchange. This exchange, associated with a quarkless three-gluon vector glueball, was identified in the comparison of proton–proton and proton–antiproton scattering. [8] [9] [10] In 2024, the X(2370) particle was determined to have mass and spin parity consistent with that of a glueball. [11] However, other exotic particle candidates such as a tetraquark could not be ruled out. [12]

Properties

In principle, it is theoretically possible for all properties of glueballs to be calculated exactly and derived directly from the equations and fundamental physical constants of quantum chromodynamics (QCD) without further experimental input. So, the predicted properties of these hypothetical particles can be described in exquisite detail using only Standard Model physics that have wide acceptance in the theoretical physics literature. But, there is considerable uncertainty in the measurement of some of the relevant key physical constants, and the QCD calculations are so difficult that solutions to these equations are almost always numerical approximations (calculated using several very different methods). This can lead to variation in theoretical predictions of glueball properties, like mass and branching ratios in glueball decays.

Constituent particles and color charge

Theoretical studies of glueballs have focused on glueballs consisting of either two gluons or three gluons, by analogy to mesons and baryons that have two and three quarks respectively. As in the case of mesons and baryons, glueballs would be QCD color charge neutral. The baryon number of a glueball is zero.

Total angular momentum

Double-gluon glueballs can have total angular momentum J = 0 (which are either scalar or pseudo-scalar) or J = 2 (tensor). Triple-gluon glueballs can have total angular momentum J = 1 (vector boson) or 3 (third-order tensor boson). All glueballs have integer total angular momentum that implies that they are bosons rather than fermions.

Glueballs are the only particles predicted by the Standard Model with total angular momentum (J) (sometimes called "intrinsic spin") that could be either 2 or 3 in their ground states, although mesons made of two quarks with J = 0 and J = 1 with similar masses have been observed and excited states of other mesons can have these values of total angular momentum.

Electric charge

All glueballs would have an electric charge of zero, as gluons themselves do not have an electric charge.

Mass and parity

Glueballs are predicted by quantum chromodynamics to be massive, despite the fact that gluons themselves have zero rest mass in the Standard Model. Glueballs with all four possible combinations of quantum numbers P (spatial parity) and C (charge parity) for every possible total angular momentum have been considered, producing at least fifteen possible glueball states including excited glueball states that share the same quantum numbers but have differing masses with the lightest states having masses as low as 1.4 GeV/c2 (for a glueball with quantum numbers J = 0, P = +1, C = +1, or equivalently J PC = 0++), and the heaviest states having masses as great as almost 5 GeV/c2 (for a glueball with quantum numbers J = 0, P = +1, C = −1, or J PC = 0+−). [5]

These masses are on the same order of magnitude as the masses of many experimentally observed mesons and baryons, as well as to the masses of the tau lepton, charm quark, bottom quark, some hydrogen isotopes, and some helium isotopes.

Stability and decay channels

Just as all Standard Model mesons and baryons, except the proton, are unstable in isolation, all glueballs are predicted by the Standard Model to be unstable in isolation, with various QCD calculations predicting the total decay width (which is functionally related to half-life) for various glueball states. QCD calculations also make predictions regarding the expected decay patterns of glueballs. [13] [14] For example, glueballs would not have radiative or two photon decays, but would have decays into pairs of pions, pairs of kaons, or pairs of eta mesons. [13]

Practical impact on macroscopic low energy physics

Feynman diagram of a glueball (G) decaying to two pions ( p ). Such decays help the study of and search for glueballs. Feynmann Diagram Glueball-to-Pion.svg
Feynman diagram of a glueball (G) decaying to two pions (
π
). Such decays help the study of and search for glueballs.

Because Standard Model glueballs are so ephemeral (decaying almost immediately into more stable decay products) and are only generated in high energy physics, glueballs only arise synthetically in the natural conditions found on Earth that humans can easily observe. They are scientifically notable mostly because they are a testable prediction of the Standard Model, and not because of phenomenological impact on macroscopic processes, or their engineering applications.

Lattice QCD simulations

Lattice QCD provides a way to study the glueball spectrum theoretically and from first principles. Some of the first quantities calculated using lattice QCD methods (in 1980) were glueball mass estimates. [16] Morningstar and Peardon [17] computed in 1999 the masses of the lightest glueballs in QCD without dynamical quarks. The three lowest states are tabulated below. The presence of dynamical quarks would slightly alter these data, but also makes the computations more difficult. Since that time calculations within QCD (lattice and sum rules) find the lightest glueball to be a scalar with mass in the range of about 1000–1700 MeV/c2. [5] Lattice predictions for scalar and pseudoscalar glueballs, including their excitations, were confirmed by Dyson–Schwinger/Bethe–Salpeter equations in Yang–Mills theory. [18]

J P C mass
0++1730±80  MeV/c2
2++2400±120 MeV/c2
0−+2590±130 MeV/c2

Experimental candidates

Particle accelerator experiments are often able to identify unstable composite particles and assign masses to those particles to a precision of approximately 10 MeV/c2, without being able to immediately assign to the particle resonance that is observed all of the properties of that particle. Scores of such particles have been detected, although particles detected in some experiments but not others can be viewed as doubtful.

Many of these candidates have been the subject of active investigation for at least eighteen years. [13] The GlueX experiment has been specifically designed to produce more definitive experimental evidence of glueballs. [19]

Some of the candidate particle resonances that could be glueballs, although the evidence is not definitive, include the following:

Vector, pseudo-vector, or tensor glueball candidates

Scalar glueball candidates

Other candidates

See also

Related Research Articles

<span class="mw-page-title-main">Gluon</span> Elementary particle that mediates the strong force

A gluon is a type of massless elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a spin of 1. Through the strong interaction, gluons bind quarks into groups according to quantum chromodynamics (QCD), forming hadrons such as protons and neutrons.

<span class="mw-page-title-main">Hadron</span> Composite subatomic particle

In particle physics, a hadron is a composite subatomic particle made of two or more quarks held together by the strong interaction. They are analogous to molecules, which are held together by the electric force. Most of the mass of ordinary matter comes from two hadrons: the proton and the neutron, while most of the mass of the protons and neutrons is in turn due to the binding energy of their constituent quarks, due to the strong force.

<span class="mw-page-title-main">Nucleon</span> Particle that makes up the atomic nucleus (proton or neutron)

In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.

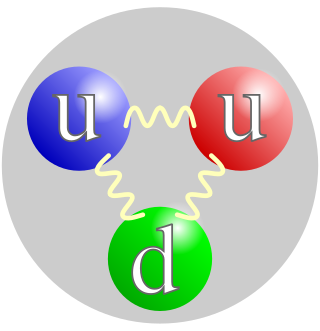
<span class="mw-page-title-main">Quark</span> Elementary particle, main constituent of matter

A quark is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. All commonly observable matter is composed of up quarks, down quarks and electrons. Owing to a phenomenon known as color confinement, quarks are never found in isolation; they can be found only within hadrons, which include baryons and mesons, or in quark–gluon plasmas. For this reason, much of what is known about quarks has been drawn from observations of hadrons.

<span class="mw-page-title-main">Quantum chromodynamics</span> Theory of the strong nuclear interactions

In theoretical physics, quantum chromodynamics (QCD) is the study of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of quantum field theory called a non-abelian gauge theory, with symmetry group SU(3). The QCD analog of electric charge is a property called color. Gluons are the force carriers of the theory, just as photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of particle physics. A large body of experimental evidence for QCD has been gathered over the years.

<span class="mw-page-title-main">Standard Model</span> Theory of forces and subatomic particles

The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

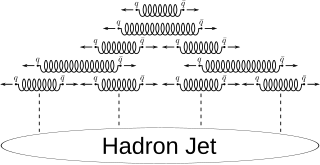
<span class="mw-page-title-main">Color confinement</span> Phenomenon in quantum chromodynamics

In quantum chromodynamics (QCD), color confinement, often simply called confinement, is the phenomenon that color-charged particles cannot be isolated, and therefore cannot be directly observed in normal conditions below the Hagedorn temperature of approximately 2 terakelvin. Quarks and gluons must clump together to form hadrons. The two main types of hadron are the mesons and the baryons. In addition, colorless glueballs formed only of gluons are also consistent with confinement, though difficult to identify experimentally. Quarks and gluons cannot be separated from their parent hadron without producing new hadrons.

<span class="mw-page-title-main">Exotic meson</span> Meson particles which do not fit into the quark model

In particle physics, exotic mesons are mesons that have quantum numbers not possible in the quark model; some proposals for non-standard quark model mesons could be:

<span class="mw-page-title-main">Quarkonium</span> Meson whose constituents are a quark and its own antiquark of the same flavor

In particle physics, quarkonium is a flavorless meson whose constituents are a heavy quark and its own antiquark, making it both a neutral particle and its own antiparticle. The name "quarkonium" is analogous to positronium, the bound state of electron and anti-electron. The particles are short-lived due to matter-antimatter annihilation.

<span class="mw-page-title-main">Pseudoscalar meson</span> Meson with total spin 0 and odd parity

In high-energy physics, a pseudoscalar meson is a meson with total spin 0 and odd parity . Pseudoscalar mesons are commonly seen in proton-proton scattering and proton-antiproton annihilation, and include the pion, kaon, eta, and eta prime particles, whose masses are known with great precision.

In high energy physics, a scalar meson is a meson with total spin 0 and even parity (usually noted as JP=0+). In contrast, pseudoscalar mesons have odd parity. The first known scalar mesons have been observed since the late 1950s, with observations of numerous light states and heavier states proliferating since the 1980s. Scalar mesons are most often observed in proton-antiproton annihilation, radiative decays of vector mesons, and meson-meson scattering.

The QCD vacuum is the quantum vacuum state of quantum chromodynamics (QCD). It is an example of a non-perturbative vacuum state, characterized by non-vanishing condensates such as the gluon condensate and the quark condensate in the complete theory which includes quarks. The presence of these condensates characterizes the confined phase of quark matter.

<span class="mw-page-title-main">Exotic hadron</span> Subatomic particles consisting of quarks and gluons

Exotic hadrons are subatomic particles composed of quarks and gluons, but which – unlike "well-known" hadrons such as protons, neutrons and mesons – consist of more than three valence quarks. By contrast, "ordinary" hadrons contain just two or three quarks. Hadrons with explicit valence gluon content would also be considered exotic. In theory, there is no limit on the number of quarks in a hadron, as long as the hadron's color charge is white, or color-neutral.

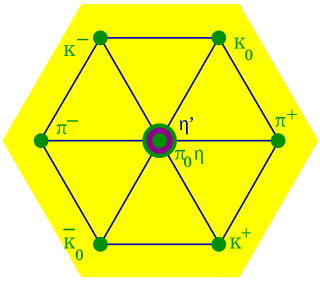
<span class="mw-page-title-main">Quark model</span> Classification scheme of hadrons

In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks that give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eightfold Way, the successful classification scheme organizing the large number of lighter hadrons that were being discovered starting in the 1950s and continuing through the 1960s. It received experimental verification beginning in the late 1960s and is a valid and effective classification of them to date. The model was independently proposed by physicists Murray Gell-Mann, who dubbed them "quarks" in a concise paper, and George Zweig, who suggested "aces" in a longer manuscript. André Petermann also touched upon the central ideas from 1963 to 1965, without as much quantitative substantiation. Today, the model has essentially been absorbed as a component of the established quantum field theory of strong and electroweak particle interactions, dubbed the Standard Model.

In particle physics, chiral symmetry breaking generally refers to the dynamical spontaneous breaking of a chiral symmetry associated with massless fermions. This is usually associated with a gauge theory such as quantum chromodynamics, the quantum field theory of the strong interaction, and it also occurs through the Brout-Englert-Higgs mechanism in the electroweak interactions of the standard model. This phenomenon is analogous to magnetization and superconductivity in condensed matter physics. The basic idea was introduced to particle physics by Yoichiro Nambu, in particular, in the Nambu–Jona-Lasinio model, which is a solvable theory of composite bosons that exhibits dynamical spontaneous chiral symmetry when a 4-fermion coupling constant becomes sufficiently large. Nambu was awarded the 2008 Nobel prize in physics "for the discovery of the mechanism of spontaneous broken symmetry in subatomic physics".

Hadron spectroscopy is the subfield of particle physics that studies the masses and decays of hadrons. Hadron spectroscopy is also an important part of the new nuclear physics. The properties of hadrons are a consequence of a theory called quantum chromodynamics (QCD).

<span class="mw-page-title-main">Stephan Narison</span> Malagasy physicist

Stephan Narison is a Malagasy theoretical high-energy physicist specialized in quantum chromodynamics (QCD), the gauge theory of strong interactions. He is the founder of the Series of International Conferences in Quantum Chromodynamics (QCD-Montpellier) and of the Series of International Conferences in High-Energy Physics (HEPMAD-Madagascar).

References

  1. ↑ Close, Frank; Page, Phillip R. (November 1998). "Glueballs". Scientific American. 279 (5): 80–85. Bibcode:1998SciAm.279e..80C. doi:10.1038/scientificamerican1198-80. JSTOR   26058158.
  2. ↑ Mathieu, Vincent; Kochelev, Nikolai; Vento, Vicente (2009). "The Physics of Glueballs". International Journal of Modern Physics E . 18 (1): 1–49. arXiv: 0810.4453 . Bibcode:2009IJMPE..18....1M. doi:10.1142/S0218301309012124. S2CID   119229404.
  3. ↑ Glueball on arxiv.org
  4. ↑ Shuryak, E. (2021). "Chapter 9". Nonperturbative Topological Phenomena in QCD and Related Theories. Springer. p. 233. ISBN   978-3030629892.
  5. 1 2 3 4 5 6 7 8 9 Ochs, Wolfgang (2013). "The status of glueballs". Journal of Physics G . 40 (4): 043001. arXiv: 1301.5183 . Bibcode:2013JPhG...40d3001O. doi:10.1088/0954-3899/40/4/043001. S2CID   73696704.
  6. ↑ Brünner, Frederic; Rebhan, Anton (2015-09-21). "Nonchiral Enhancement of Scalar Glueball Decay in the Witten–Sakai–Sugimoto Model". Physical Review Letters. 115 (13): 131601. arXiv: 1504.05815 . Bibcode:2015PhRvL.115m1601B. doi:10.1103/PhysRevLett.115.131601. PMID   26451541. S2CID   14043746.
  7. 1 2 Hsiao, Y.K.; Geng, C.Q. (2013). "Identifying glueball at 3.02 GeV in baryonic B decays". Physics Letters B. 727 (1–3): 168–171. arXiv: 1302.3331 . Bibcode:2013PhLB..727..168H. doi:10.1016/j.physletb.2013.10.008. S2CID   119235634.
  8. ↑ D0 collaboration; TOTEM Collaboration; Abazov, V. M.; Abbott, B.; Acharya, B. S.; Adams, M.; Adams, T.; Agnew, J. P.; Alexeev, G. D.; Alkhazov, G.; Alton, A. (2021-08-04). "Odderon Exchange from Elastic Scattering Differences between pp and pp Data at 1.96 TeV and from pp Forward Scattering Measurements". Physical Review Letters. 127 (6): 062003. arXiv: 2012.03981 . doi:10.1103/PhysRevLett.127.062003. hdl: 10138/333366 . PMID   34420329. S2CID   237267938.
  9. ↑ Chalmers, Matthew (9 March 2021). "Odderon discovered". CERN Courier. Retrieved 13 April 2021.
  10. ↑ Csörgő, T.; Novák, T.; Ster, A.; Szanyi, I. (23 February 2021). "Evidence of Odderon-exchange from scaling properties of elastic scattering at TeV energies". The European Physical Journal C. 81 (180). Springer Nature Switzerland AG.: 180. arXiv: 1912.11968 . Bibcode:2021EPJC...81..180C. doi: 10.1140/epjc/s10052-021-08867-6 . ISSN   1434-6052.
  11. ↑ Ablikim, M.; et al. (BESIII Collaboration) (May 2024). "Determination of Spin-Parity Quantum Numbers of X(2370) as 0−+ from J/ψ → γK0
    S    K0
    η′". Physical Review Letters. 132 (18): 181901. arXiv: 2312.05324 . doi:10.1103/PhysRevLett.132.181901.
  12. ↑ "New particle at last! Physicists detect the first "glueball"". Big Think. 2024-05-07. Retrieved 2024-05-08.
  13. 1 2 3 Taki, Walter (1996). "Search for Glueballs" (PDF). Stanford Linear Accelerator. Stanford University.
  14. ↑ Eshraim, Walaa I.; Janowski, Stanislaus (2013). "Branching ratios of the pseudoscalar glueball with a mass of 2.6 GeV". arXiv: 1301.3345 [hep-ph].
  15. ↑ Cohen, Thomas; Llanes-Estrada, Felipe J.; Pelaez, J. R.; Ruiz De Elvira, J. (2014). "Non-ordinary light meson couplings and the 1/Nc expansion". Physical Review D. 90 (3): 036003. arXiv: 1405.4831 . Bibcode:2014PhRvD..90c6003C. doi:10.1103/PhysRevD.90.036003. S2CID   53313057.
  16. ↑ Berg, B. (1980). "Plaquette-plaquette correlations in the SU(2) lattice gauge theory". Physics Letters B. 97 (3–4): 401–404. Bibcode:1980PhLB...97..401B. doi:10.1016/0370-2693(80)90628-0.
  17. ↑ Morningstar, Colin J.; Peardon, Mike (1999). "Glueball spectrum from an anisotropic lattice study". Physical Review D . 60 (3): 034509. arXiv: hep-lat/9901004 . Bibcode:1999PhRvD..60c4509M. doi:10.1103/PhysRevD.60.034509. S2CID   18787544.
  18. ↑ Huber, Markus Q.; Fischer, Christian S.; Sanchis-Alepuz, Hèlios (2020). "Spectrum of scalar and pseudoscalar glueballs from functional methods". The European Physical Journal C. 80 (11): 1077. arXiv: 2004.00415 . Bibcode:2020EPJC...80.1077H. doi:10.1140/epjc/s10052-020-08649-6. PMID   33239962.
  19. ↑ "The Physics of GlueX". Archived from the original on 2020-02-22. Retrieved 2015-05-07.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.