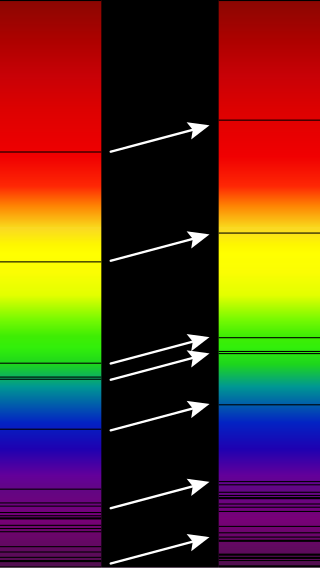
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation. The opposite change, a decrease in wavelength and increase in frequency and energy, is known as a blueshift, or negative redshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. The main causes of electromagnetic redshift in astronomy and cosmology are the relative motions of radiation sources, which give rise to the relativistic Doppler effect, and gravitational potentials, which gravitationally redshift escaping radiation. All sufficiently distant light sources show cosmological redshift corresponding to recession speeds proportional to their distances from Earth, a fact known as Hubble's law that implies the universe is expanding.

Observations show that the expansion of the universe is accelerating, such that the velocity at which a distant galaxy recedes from the observer is continuously increasing with time. The accelerated expansion of the universe was discovered in 1998 by two independent projects, the Supernova Cosmology Project and the High-Z Supernova Search Team, which used distant type Ia supernovae to measure the acceleration. The idea was that as type Ia supernovae have almost the same intrinsic brightness, and since objects that are farther away appear dimmer, the observed brightness of these supernovae can be used to measure the distance to them. The distance can then be compared to the supernovae's cosmological redshift, which measures how much the universe has expanded since the supernova occurred; the Hubble law established that the farther away that an object is, the faster it is receding. The unexpected result was that objects in the universe are moving away from one another at an accelerating rate. Cosmologists at the time expected that recession velocity would always be decelerating, due to the gravitational attraction of the matter in the universe. Three members of these two groups have subsequently been awarded Nobel Prizes for their discovery. Confirmatory evidence has been found in baryon acoustic oscillations, and in analyses of the clustering of galaxies.
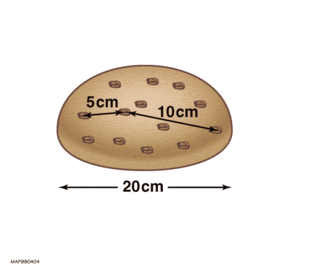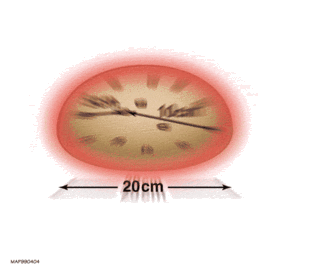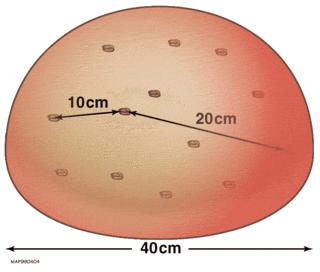
Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving away from Earth. The velocity of the galaxies has been determined by their redshift, a shift of the light they emit toward the red end of the visible light spectrum. The discovery of Hubble's law is attributed to Edwin Hubble's work published in 1929.

A gravitational singularity, spacetime singularity or simply singularity is a condition in which gravity is predicted to be so intense that spacetime itself would break down catastrophically. As such, a singularity is by definition no longer part of the regular spacetime and cannot be determined by "where" or "when". Gravitational singularities exist at a junction between general relativity and quantum mechanics; therefore, the properties of the singularity cannot be described without an established theory of quantum gravity. Trying to find a complete and precise definition of singularities in the theory of general relativity, the current best theory of gravity, remains a difficult problem. A singularity in general relativity can be defined by the scalar invariant curvature becoming infinite or, better, by a geodesic being incomplete.
The particle horizon is the maximum distance from which light from particles could have traveled to the observer in the age of the universe. Much like the concept of a terrestrial horizon, it represents the boundary between the observable and the unobservable regions of the universe, so its distance at the present epoch defines the size of the observable universe. Due to the expansion of the universe, it is not simply the age of the universe times the speed of light, but rather the speed of light times the conformal time. The existence, properties, and significance of a cosmological horizon depend on the particular cosmological model.

The Friedmann–Lemaître–Robertson–Walker metric is a metric based on an exact solution of the Einstein field equations of general relativity. The metric describes a homogeneous, isotropic, expanding universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are variously grouped as Friedmann, Friedmann–Robertson–Walker (FRW), Robertson–Walker (RW), or Friedmann–Lemaître (FL). This model is sometimes called the Standard Model of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. The FLRW model was developed independently by the named authors in the 1920s and 1930s.
The expansion of the universe is parametrized by a dimensionless scale factor. Also known as the cosmic scale factor or sometimes the Robertson–Walker scale factor, this is a key parameter of the Friedmann equations.

The Lambda-CDM, Lambda cold dark matter, or ΛCDM model is a mathematical model of the Big Bang theory with three major components:
- a cosmological constant, denoted by lambda (Λ), associated with dark energy
- the postulated cold dark matter, denoted by CDM
- ordinary matter

The flatness problem is a cosmological fine-tuning problem within the Big Bang model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that small deviations from these values would have extreme effects on the appearance of the universe at the current time.

The Friedmann equations, also known as the Friedmann–Lemaître (FL) equations, are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity. They were first derived by Alexander Friedmann in 1922 from Einstein's field equations of gravitation for the Friedmann–Lemaître–Robertson–Walker metric and a perfect fluid with a given mass density ρ and pressure p. The equations for negative spatial curvature were given by Friedmann in 1924.
The Gödel metric, also known as the Gödel solution or Gödel universe, is an exact solution, found in 1949 by Kurt Gödel, of the Einstein field equations in which the stress–energy tensor contains two terms: the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a negative cosmological constant.
In general relativity, the metric tensor is the fundamental object of study. The metric captures all the geometric and causal structure of spacetime, being used to define notions such as time, distance, volume, curvature, angle, and separation of the future and the past.
In physical cosmology, cosmological perturbation theory is the theory by which the evolution of structure is understood in the Big Bang model. Cosmological perturbation theory may be broken into two categories: Newtonian or general relativistic. Each case uses its governing equations to compute gravitational and pressure forces which cause small perturbations to grow and eventually seed the formation of stars, quasars, galaxies and clusters. Both cases apply only to situations where the universe is predominantly homogeneous, such as during cosmic inflation and large parts of the Big Bang. The universe is believed to still be homogeneous enough that the theory is a good approximation on the largest scales, but on smaller scales more involved techniques, such as N-body simulations, must be used. When deciding whether to use general relativity for perturbation theory, note that Newtonian physics is only applicable in some cases such as for scales smaller than the Hubble horizon, where spacetime is sufficiently flat, and for which speeds are non-relativistic.

The expansion of the universe is the increase in distance between gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion, so it does not mean that the universe expands "into" anything or that space exists "outside" it. To any observer in the universe, it appears that all but the nearest galaxies recede at speeds that are proportional to their distance from the observer, on average. While objects cannot move faster than light, this limitation applies only with respect to local reference frames and does not limit the recession rates of cosmologically distant objects.

The deceleration parameter in cosmology is a dimensionless measure of the cosmic acceleration of the expansion of space in a Friedmann–Lemaître–Robertson–Walker universe. It is defined by: where is the scale factor of the universe and the dots indicate derivatives by proper time. The expansion of the universe is said to be "accelerating" if , and in this case the deceleration parameter will be negative. The minus sign and name "deceleration parameter" are historical; at the time of definition was expected to be negative, so a minus sign was inserted in the definition to make positive in that case. Since the evidence for the accelerating universe in the 1998–2003 era, it is now believed that is positive therefore the present-day value is negative. In general varies with cosmic time, except in a few special cosmological models; the present-day value is denoted .
The Milne model was a special-relativistic cosmological model proposed by Edward Arthur Milne in 1935. It is mathematically equivalent to a special case of the FLRW model in the limit of zero energy density and it obeys the cosmological principle. The Milne model is also similar to Rindler space in that both are simple re-parameterizations of flat Minkowski space.

Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly observable, but is more convenient for calculations. The distance measures discussed here all reduce to the common notion of Euclidean distance at low redshift.

In cosmology, baryon acoustic oscillations (BAO) are fluctuations in the density of the visible baryonic matter of the universe, caused by acoustic density waves in the primordial plasma of the early universe. In the same way that supernovae provide a "standard candle" for astronomical observations, BAO matter clustering provides a "standard ruler" for length scale in cosmology. The length of this standard ruler is given by the maximum distance the acoustic waves could travel in the primordial plasma before the plasma cooled to the point where it became neutral atoms, which stopped the expansion of the plasma density waves, "freezing" them into place. The length of this standard ruler can be measured by looking at the large scale structure of matter using astronomical surveys. BAO measurements help cosmologists understand more about the nature of dark energy by constraining cosmological parameters.
In astrophysics, the virial mass is the mass of a gravitationally bound astrophysical system, assuming the virial theorem applies. In the context of galaxy formation and dark matter halos, the virial mass is defined as the mass enclosed within the virial radius of a gravitationally bound system, a radius within which the system obeys the virial theorem. The virial radius is determined using a "top-hat" model. A spherical "top hat" density perturbation destined to become a galaxy begins to expand, but the expansion is halted and reversed due to the mass collapsing under gravity until the sphere reaches equilibrium – it is said to be virialized. Within this radius, the sphere obeys the virial theorem which says that the average kinetic energy is equal to minus one half times the average potential energy, , and this radius defines the virial radius.
















