
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal.
A discrete element method (DEM), also called a distinct element method, is any of a family of numerical methods for computing the motion and effect of a large number of small particles. Though DEM is very closely related to molecular dynamics, the method is generally distinguished by its inclusion of rotational degrees-of-freedom as well as stateful contact, particle deformation and often complicated geometries. With advances in computing power and numerical algorithms for nearest neighbor sorting, it has become possible to numerically simulate millions of particles on a single processor. Today DEM is becoming widely accepted as an effective method of addressing engineering problems in granular and discontinuous materials, especially in granular flows, powder mechanics, ice and rock mechanics. DEM has been extended into the Extended Discrete Element Method taking heat transfer, chemical reaction and coupling to CFD and FEM into account.

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.
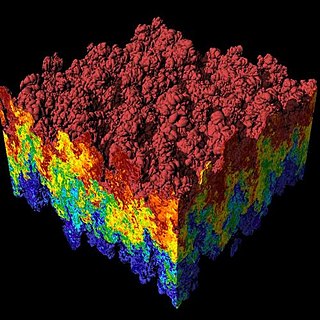
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used, to distinguish over hybrid systems such as those that combine neural nets and fuzzy logic, or electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.
Torsional vibration is the angular vibration of an object - commonly a shaft - along its axis of rotation. Torsional vibration is often a concern in power transmission systems using rotating shafts or couplings, where it can cause failures if not controlled. A second effect of torsional vibrations applies to passenger cars. Torsional vibrations can lead to seat vibrations or noise at certain speeds. Both reduce the comfort.

Fluid–structure interaction (FSI) is the interaction of some movable or deformable structure with an internal or surrounding fluid flow. Fluid–structure interactions can be stable or oscillatory. In oscillatory interactions, the strain induced in the solid structure causes it to move such that the source of strain is reduced, and the structure returns to its former state only for the process to repeat.
Discontinuous deformation analysis (DDA) is a type of discrete element method (DEM) originally proposed by Shi in 1988. DDA is somewhat similar to the finite element method for solving stress-displacement problems, but accounts for the interaction of independent particles (blocks) along discontinuities in fractured and jointed rock masses. DDA is typically formulated as a work-energy method, and can be derived using the principle of minimum potential energy or by using Hamilton's principle. Once the equations of motion are discretized, a step-wise linear time marching scheme in the Newmark family is used for the solution of the equations of motion. The relation between adjacent blocks is governed by equations of contact interpenetration and accounts for friction. DDA adopts a stepwise approach to solve for the large displacements that accompany discontinuous movements between blocks. The blocks are said to be "simply deformable". Since the method accounts for the inertial forces of the blocks' mass, it can be used to solve the full dynamic problem of block motion.
Multibody system is the study of the dynamic behavior of interconnected rigid or flexible bodies, each of which may undergo large translational and rotational displacements.
Dynamic simulation is the use of a computer program to model the time-varying behavior of a dynamical system. The systems are typically described by ordinary differential equations or partial differential equations. A simulation run solves the state-equation system to find the behavior of the state variables over a specified period of time. The equation is solved through numerical integration methods to produce the transient behavior of the state variables. Simulation of dynamic systems predicts the values of model-system state variables, as they are determined by the past state values. This relationship is found by creating a model of the system.
In rigid-body dynamics, the Painlevé paradox is the paradox that results from inconsistencies between the contact and Coulomb models of friction. It is named for former French prime minister and mathematician Paul Painlevé.
The material point method (MPM) is a numerical technique used to simulate the behavior of solids, liquids, gases, and any other continuum material. Especially, it is a robust spatial discretization method for simulating multi-phase (solid-fluid-gas) interactions. In the MPM, a continuum body is described by a number of small Lagrangian elements referred to as 'material points'. These material points are surrounded by a background mesh/grid that is used to calculate terms such as the deformation gradient. Unlike other mesh-based methods like the finite element method, finite volume method or finite difference method, the MPM is not a mesh based method and is instead categorized as a meshless/meshfree or continuum-based particle method, examples of which are smoothed particle hydrodynamics and peridynamics. Despite the presence of a background mesh, the MPM does not encounter the drawbacks of mesh-based methods which makes it a promising and powerful tool in computational mechanics.
In mathematics, differential inclusions are a generalization of the concept of ordinary differential equation of the form
Nanomechanics is a branch of nanoscience studying fundamental mechanical properties of physical systems at the nanometer scale. Nanomechanics has emerged on the crossroads of biophysics, classical mechanics, solid-state physics, statistical mechanics, materials science, and quantum chemistry. As an area of nanoscience, nanomechanics provides a scientific foundation of nanotechnology.
In contact mechanics, the term unilateral contact, also called unilateral constraint, denotes a mechanical constraint which prevents penetration between two rigid/flexible bodies. Constraints of this kind are omnipresent in non-smooth multibody dynamics applications, such as granular flows, legged robot, vehicle dynamics, particle damping, imperfect joints, or rocket landings. In these applications, the unilateral constraints result in impacts happening, therefore requiring suitable methods to deal with such constraints.
Non-smooth mechanics is a modeling approach in mechanics which does not require the time evolutions of the positions and of the velocities to be smooth functions. Due to possible impacts, the velocities of the mechanical system are allowed to undergo jumps at certain time instants in order to fulfill the kinematical restrictions. Consider for example a rigid model of a ball which falls on the ground. Just before the impact between ball and ground, the ball has non-vanishing pre-impact velocity. At the impact time instant, the velocity must jump to a post-impact velocity which is at least zero, or else penetration would occur. Non-smooth mechanical models are often used in contact dynamics.

SICONOS is an Open Source scientific software primarily targeted at modeling and simulating non-smooth dynamical systems (NSDS):

Jean Jacques Moreau was a French mathematician and mechanician. He normally published under the name J. J. Moreau.
Multibody simulation (MBS) is a method of numerical simulation in which multibody systems are composed of various rigid or elastic bodies. Connections between the bodies can be modeled with kinematic constraints or force elements. Unilateral constraints and Coulomb-friction can also be used to model frictional contacts between bodies. Multibody simulation is a useful tool for conducting motion analysis. It is often used during product development to evaluate characteristics of comfort, safety, and performance. For example, multibody simulation has been widely used since the 1990s as a component of automotive suspension design. It can also be used to study issues of biomechanics, with applications including sports medicine, osteopathy, and human-machine interaction.

MSC ADAMS is a multibody dynamics simulation software system. It is currently owned by MSC Software Corporation. The simulation software solver runs mainly on Fortran and more recently C++ as well. According to the publisher, Adams is the most widely used multibody dynamics simulation software. The software package runs on both Windows and Linux.












