Bond convexity

Last updated

In finance, bond convexity is a measure of the non-linear relationship of bond prices to changes in interest rates, and is defined as the second derivative of the price of the bond with respect to interest rates (duration is the first derivative). In general, the higher the duration, the more sensitive the bond price is to the change in interest rates. Bond convexity is one of the most basic and widely used forms of convexity in finance. Convexity was based on the work of Hon-Fei Lai and popularized by Stanley Diller. [1]

Contents

Calculation of convexity

Duration is a linear measure or 1st derivative of how the price of a bond changes in response to interest rate changes. As interest rates change, the price is not likely to change linearly, but instead it would change over some curved function of interest rates. The more curved the price function of the bond is, the more inaccurate duration is as a measure of the interest rate sensitivity. [2]

Convexity is a measure of the curvature or 2nd derivative of how the price of a bond varies with interest rate, i.e. how the duration of a bond changes as the interest rate changes. [3] Specifically, one assumes that the interest rate is constant across the life of the bond and that changes in interest rates occur evenly. Using these assumptions, duration can be formulated as the first derivative of the price function of the bond with respect to the interest rate in question. Then the convexity would be the second derivative of the price function with respect to the interest rate. [2]

Convexity does not assume the relationship between Bond value and interest rates to be linear. [4] In actual markets, the assumption of constant interest rates and even changes is not correct, and more complex models are needed to actually price bonds. However, these simplifying assumptions allow one to quickly and easily calculate factors which describe the sensitivity of the bond prices to interest rate changes. [5]

Why bond convexities may differ

The price sensitivity to parallel changes in the term structure of interest rates is highest with a zero-coupon bond and lowest with an amortizing bond (where the payments are front-loaded). [6] Although the amortizing bond and the zero-coupon bond have different sensitivities at the same maturity, if their final maturities differ so that they have identical bond durations then they will have identical sensitivities. [7] That is, their prices will be affected equally by small, first-order, (and parallel) yield curve shifts. They will, however, start to change by different amounts with each further incremental parallel rate shift due to their differing payment dates and amounts. [8]

For two bonds with the same par value, coupon, and maturity, convexity may differ depending on what point on the price yield curve they are located. [9]

Mathematical definition

If the flat floating interest rate is r and the bond price is B, then the convexityC is defined as [10]

Another way of expressing C is in terms of the modified duration D:

Therefore,

leaving

Where D is a Modified Duration

How bond duration changes with a changing interest rate

Return to the standard definition of modified duration: [11]

where P(i) is the present value of coupon i, and t(i) is the future payment date.

As the interest rate increases, the present value of longer-dated payments declines in relation to earlier coupons (by the discount factor between the early and late payments). [12] However, bond price also declines when interest rate increases, but changes in the present value of sum of each coupons times timing (the numerator in the summation) are larger than changes in the bond price (the denominator in the summation). Therefore, increases in r must decrease the duration (or, in the case of zero-coupon bonds, leave the unmodified duration constant). [13] [14] Note that the modified duration D differs from the regular duration by the factor one over 1 + r (shown above), which also decreases as r is increased.

Given the relation between convexity and duration above, conventional bond convexities must always be positive. [15]

The positivity of convexity can also be proven analytically for basic interest rate securities. For example, under the assumption of a flat yield curve one can write the value of a coupon-bearing bond as , where Ci stands for the coupon paid at time ti. Then it is easy to see that

Note that this conversely implies the negativity of the derivative of duration by differentiating .

Application of convexity

  1. Convexity is a risk management figure, used similarly to the way 'gamma' is used in derivatives risks management; it is a number used to manage the market risk a bond portfolio is exposed to. If the combined convexity and duration of a trading book is high, so is the risk. [16] However, if the combined convexity and duration are low, the book is hedged, and little money will be lost even if fairly substantial interest movements occur. (Parallel in the yield curve) [17]
  2. The second-order approximation of bond price movements due to rate changes uses the convexity:

Effective convexity

For a bond with an embedded option, a yield to maturity based calculation of convexity (and of duration) does not consider how changes in the yield curve will alter the cash flows due to option exercise. To address this, an effective convexity must be calculated numerically. [18] Effective convexity is a discrete approximation of the second derivative of the bond's value as a function of the interest rate: [18]

where is the bond value as calculated using an option pricing model, is the amount that yield changes, and are the values that the bond will take if the yield falls by or rises by , respectively (a parallel shift).

These values are typically found using a tree-based model, built for the entire yield curve, and therefore capturing exercise behavior at each point in the option's life as a function of both time and interest rates; [19] [20] see Lattice model (finance) § Interest rate derivatives.

See also

Related Research Articles

In mathematical finance, the Greeks are the quantities representing the sensitivity of the price of a derivative instrument such as an option to changes in one or more underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are denoted by Greek letters. Collectively these have also been called the risk sensitivities, risk measures or hedge parameters.

In finance, a convertible bond, convertible note, or convertible debt is a type of bond that the holder can convert into a specified number of shares of common stock in the issuing company or cash of equal value. It is a hybrid security with debt- and equity-like features. It originated in the mid-19th century, and was used by early speculators such as Jacob Little and Daniel Drew to counter market cornering.

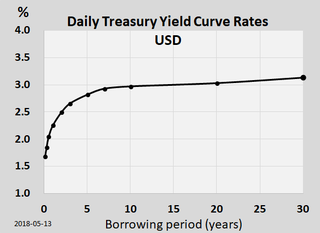
<span class="mw-page-title-main">Yield curve</span> Relationships among bond yields of different maturities

In finance, the yield curve is a graph which depicts how the yields on debt instruments – such as bonds – vary as a function of their years remaining to maturity. Typically, the graph's horizontal or x-axis is a time line of months or years remaining to maturity, with the shortest maturity on the left and progressively longer time periods on the right. The vertical or y-axis depicts the annualized yield to maturity.

Rational pricing is the assumption in financial economics that asset prices – and hence asset pricing models – will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away". This assumption is useful in pricing fixed income securities, particularly bonds, and is fundamental to the pricing of derivative instruments.

Bond valuation is the process by which an investor arrives at an estimate of the theoretical fair value, or intrinsic worth, of a bond. As with any security or capital investment, the theoretical fair value of a bond is the present value of the stream of cash flows it is expected to generate. Hence, the value of a bond is obtained by discounting the bond's expected cash flows to the present using an appropriate discount rate.

In finance, the duration of a financial asset that consists of fixed cash flows, such as a bond, is the weighted average of the times until those fixed cash flows are received. When the price of an asset is considered as a function of yield, duration also measures the price sensitivity to yield, the rate of change of price with respect to yield, or the percentage change in price for a parallel shift in yields.

<span class="mw-page-title-main">Short-rate model</span>

A short-rate model, in the context of interest rate derivatives, is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written .

In finance, interest rate immunization is a portfolio management strategy designed to take advantage of the offsetting effects of interest rate risk and reinvestment risk.

In Finance, and accounting, and particularly in asset and liability management (ALM), the duration gap is the difference between the duration - i.e. the average maturity - of assets and liabilities held by a financial entity. A related approach is to see the "duration gap" as the difference in the price sensitivity of interest-yielding assets and the price sensitivity of liabilities to a change in market interest rates (yields).

Monte Carlo methods are used in corporate finance and mathematical finance to value and analyze (complex) instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining the distribution of their value over the range of resultant outcomes. This is usually done by help of stochastic asset models. The advantage of Monte Carlo methods over other techniques increases as the dimensions of the problem increase.

The forward rate is the future yield on a bond. It is calculated using the yield curve. For example, the yield on a three-month Treasury bill six months from now is a forward rate.

Fixed income analysis is the process of determining the value of a debt security based on an assessment of its risk profile, which can include interest rate risk, risk of the issuer failing to repay the debt, market supply and demand for the security, call provisions and macroeconomic considerations affecting its value in the future. It also addresses the likely price behavior in hedging portfolios. Based on such an analysis, a fixed income analyst tries to reach a conclusion as to whether to buy, sell, hold, hedge or avoid the particular security.

The Z-spread, ZSPRD, zero-volatility spread, or yield curve spread of a bond is the parallel shift or spread over the zero-coupon Treasury yield curve required for discounting a pre-determined cash flow schedule to arrive at its present market price. The Z-spread is also widely used in the credit default swap (CDS) market as a measure of credit spread that is relatively insensitive to the particulars of specific corporate or government bonds.

<span class="mw-page-title-main">Cox–Ingersoll–Ross model</span> Stochastic model for the evolution of financial interest rates

In mathematical finance, the Cox–Ingersoll–Ross (CIR) model describes the evolution of interest rates. It is a type of "one factor model" as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives. It was introduced in 1985 by John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model.

Fixed-income attribution is the process of measuring returns generated by various sources of risk in a fixed income portfolio, particularly when multiple sources of return are active at the same time.

In finance, bootstrapping is a method for constructing a (zero-coupon) fixed-income yield curve from the prices of a set of coupon-bearing products, e.g. bonds and swaps.

<span class="mw-page-title-main">Black–Scholes equation</span> Partial differential equation in mathematical finance

In mathematical finance, the Black–Scholes equation is a partial differential equation (PDE) governing the price evolution of derivatives under the Black–Scholes model. Broadly speaking, the term may refer to a similar PDE that can be derived for a variety of options, or more generally, derivatives.

In finance, par yield is the yield on a fixed income security assuming that its market price is equal to par value. Par yield is used to derive the U.S. Treasury’s daily official “Treasury Par Yield Curve Rates”, which are used by investors to price debt securities traded in public markets, and by lenders to set interest rates on many other types of debt, including bank loans and mortgages.

An affine term structure model is a financial model that relates zero-coupon bond prices to a spot rate model. It is particularly useful for deriving the yield curve – the process of determining spot rate model inputs from observable bond market data. The affine class of term structure models implies the convenient form that log bond prices are linear functions of the spot rate.

In finance, a zero coupon swap (ZCS) is an interest rate derivative (IRD). In particular it is a linear IRD, that in its specification is very similar to the much more widely traded interest rate swap (IRS).

References

  1. ↑ Diller, Stanley (1991), Parametric Analysis of Fixed Income Securities, in Dattatreya, Ravi (ed.) Fixed Income Analytics: State-of-the-Art Debt Analysis and Valuation Modeling, Probus Publishing
  2. 1 2 Brooks, Robert; Attinger, Bill (1992-07-01). "Using Duration and Convexity in the Analysis of Callable Convertible Bonds". Financial Analysts Journal. 48 (4): 74–77. doi:10.2469/faj.v48.n4.74. ISSN   0015-198X.
  3. ↑ Pelsser, Antoon (2003-02-04). "Mathematical foundation of convexity correction". Quantitative Finance. 3 (1). doi:10.1088/1469-7688/3/1/306/meta. eISSN   1469-7696 . Retrieved 2023-09-30.
  4. ↑ Udegbunam, Raphael I.; Oaikhenan, Hassan E. (2012-03-13). "Interest Rate Risk of Stock Prices in Nigeria: Empirical Test of the Duration and Convexity Model". Journal of Emerging Market Finance. 11 (1): 93–113. doi:10.1177/097265271101100104. ISSN   0972-6527.
  5. ↑ Weil, Lawrence Fisher, Roman L. (1982), "Coping with the Risk of Interest-Rate Fluctuations: Returns to Bondholders From Naïve and Optimal Strategies*", Bond Duration and Immunization, Routledge, doi:10.4324/9781315145976-11/coping-risk-interest-rate-fluctuations-returns-bondholders-na%C3%AFve-optimal-strategies-lawrence-fisher-roman-weil, ISBN   978-1-315-14597-6 , retrieved 2023-10-02{{citation}}: CS1 maint: multiple names: authors list (link)
  6. ↑ Dai, Qiang; Singleton, Kenneth J.; Yang, Wei (2007-04-12). "Regime Shifts in a Dynamic Term Structure Model of U.S. Treasury Bond Yields". Review of Financial Studies. 20 (5): 1669–1706. doi:10.1093/rfs/hhm021. ISSN   0893-9454.
  7. ↑ Whittingham, M. (1997). "The Canadian market for zero-coupon bonds" (PDF). Bank of Canada Review: 47–62.
  8. ↑ Phoa, Wesley; Shearer, Michael (1997-12-31). "A Note on Arbitrary Yield Curve Reshaping Sensitivities Using Key Rate Durations". The Journal of Fixed Income. 7 (3): 67–71. doi:10.3905/jfi.1997.408212. ISSN   1059-8596.
  9. ↑ Livingston, Miles (1979-03-01). "Bond Taxation and the Shape of the Yield‐to‐Maturity Curve". The Journal of Finance. 34 (1): 189–196. doi:10.1111/j.1540-6261.1979.tb02079.x. ISSN   0022-1082.
  10. ↑ Fong, H. Gifford; Vasicek, Oldrich A. (1991-07-31). "Fixed–income volatility management". The Journal of Portfolio Management. 17 (4): 41–46. doi:10.3905/jpm.1991.409345. ISSN   0095-4918.
  11. ↑ Fabozzi, Frank J., ed. (2008-09-15). Handbook of Finance (1 ed.). Wiley. doi:10.1002/9780470404324.hof003014. ISBN   978-0-470-04256-4.
  12. ↑ Shea, Gary S. (1984). "Pitfalls in Smoothing Interest Rate Term Structure Data: Equilibrium Models and Spline Approximations". The Journal of Financial and Quantitative Analysis. 19 (3): 253–269. doi:10.2307/2331089. ISSN   0022-1090.
  13. ↑ Geiger, Felix (2011), Geiger, Felix (ed.), "The Theory of the Term Structure of Interest Rates", The Yield Curve and Financial Risk Premia: Implications for Monetary Policy, Lecture Notes in Economics and Mathematical Systems, Berlin, Heidelberg: Springer, pp. 43–82, doi:10.1007/978-3-642-21575-9_3, ISBN   978-3-642-21575-9 , retrieved 2023-11-06
  14. ↑ Swishchuk, Anatoliy (2009-01-04). "Levy-Based Interest Rate Derivatives: Change of Time Method and PIDEs" (PDF). Econometrics: Single Equation Models eJournal. doi:10.2139/ssrn.1322532 – via SSRN.
  15. ↑ Grantier, Bruce J. (1988-11-01). "Convexity and Bond Performance: The Benter the Better". Financial Analysts Journal. 44 (6): 79–81. doi:10.2469/faj.v44.n6.79. ISSN   0015-198X.
  16. ↑ Fong, H. Gifford; Vasicek, Oldrich A. (1991-07-31). "Fixed–income volatility management". The Journal of Portfolio Management. 17 (4): 41–46. doi:10.3905/jpm.1991.409345. ISSN   0095-4918.
  17. ↑ Smit, Linda; Swart, Barbara (2006-01-31). "Calculating the Price of Bond Convexity". The Journal of Portfolio Management. 32 (2): 99–106. doi:10.3905/jpm.2006.611809. ISSN   0095-4918.
  18. 1 2 Fabozzi, Frank J., ed. (2008-09-15). Handbook of Finance (1 ed.). Wiley. doi:10.1002/9780470404324.hof003014. ISBN   978-0-470-04256-4.
  19. ↑ Choudhry, Moorad (2004-01-01), Choudhry, Moorad (ed.), "3 - The dynamics of asset prices", Advanced Fixed Income Analysis, Oxford: Butterworth-Heinemann, pp. 35–54, doi:10.1016/b978-075066263-5.50005-7, ISBN   978-0-7506-6263-5 , retrieved 2023-11-06
  20. ↑ Miltersen, Kristian R.; Schwartz, Eduardo S. (1998). "Pricing of Options on Commodity Futures with Stochastic Term Structures of Convenience Yields and Interest Rates". The Journal of Financial and Quantitative Analysis. 33 (1): 33–59. doi:10.2307/2331377. ISSN   0022-1090.

Further reading

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.