Banked turn

This article needs additional citations for verification . Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources:  "Banked turn"  –  news · newspapers · books · scholar · JSTOR (February 2009) ( Learn how and when to remove this message )

A banked turn (or banking turn) is a turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn. For a road or railroad this is usually due to the roadbed having a transverse down-slope towards the inside of the curve. The bank angle is the angle at which the vehicle is inclined about its longitudinal axis with respect to the horizontal.

Contents

• Turn on flat surfaces
• Frictionless banked turn
• Banked turn with friction
• Banked turn in aeronautics
• Banked turn in athletics
• See also
• References
• Further reading
• External links

Turn on flat surfaces

If the bank angle is zero, the surface is flat and the normal force is vertically upward. The only force keeping the vehicle turning on its path is friction, or traction. This must be large enough to provide the centripetal force, a relationship that can be expressed as an inequality, assuming the car is driving in a circle of radius ${\displaystyle r}$:

${\displaystyle \mu mg>{mv^{2} \over r}.}$

The expression on the right hand side is the centripetal acceleration multiplied by mass, the force required to turn the vehicle. The left hand side is the maximum frictional force, which equals the coefficient of friction ${\displaystyle \mu }$ multiplied by the normal force. Rearranging the maximum cornering speed is

${\displaystyle v<{\sqrt {r\mu g}}.}$

Note that ${\displaystyle \mu }$ can be the coefficient for static or dynamic friction. In the latter case, where the vehicle is skidding around a bend, the friction is at its limit and the inequalities becomes equations. This also ignores effects such as downforce, which can increase the normal force and cornering speed.

Frictionless banked turn

As opposed to a vehicle riding along a flat circle, inclined edges add an additional force that keeps the vehicle in its path and prevents a car from being "dragged into" or "pushed out of" the circle (or a railroad wheel from moving sideways so as to nearly rub on the wheel flange). This force is the horizontal component of the vehicle's normal force (N). In the absence of friction, the normal force is the only one acting on the vehicle in the direction of the center of the circle. Therefore, as per Newton's second law, we can set the horizontal component of the normal force equal to mass multiplied by centripetal acceleration: ^[1]

${\displaystyle {mv^{2} \over r}=N\sin \theta }$

Because there is no motion in the vertical direction, the sum of all vertical forces acting on the system must be zero. Therefore, we can set the vertical component of the vehicle's normal force equal to its weight: ^[1]

${\displaystyle N\cos \theta =mg}$

Solving the above equation for the normal force and substituting this value into our previous equation, we get:

${\displaystyle {mv^{2} \over r}={mg\tan \theta }}$

This is equivalent to:

${\displaystyle {v^{2} \over r}={g\tan \theta }}$

Solving for velocity we have:

${\displaystyle v={\sqrt {rg\tan \theta }}}$

This provides the velocity that in the absence of friction and with a given angle of incline and radius of curvature, will ensure that the vehicle will remain in its designated path. The magnitude of this velocity is also known as the "rated speed" (or "balancing speed" for railroads) of a turn or curve. ^[2] Notice that the rated speed of the curve is the same for all massive objects, and a curve that is not inclined will have a rated speed of 0.

Banked turn with friction

When considering the effects of friction on the system, once again we need to note which way the friction force is pointing. When calculating a maximum velocity for our automobile, friction will point down the incline and towards the center of the circle. Therefore, we must add the horizontal component of friction to that of the normal force. The sum of these two forces is our new net force in the direction of the center of the turn (the centripetal force):

${\displaystyle \underbrace {{mv^{2} \over r}=N\sin \theta } _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\cos \theta } _{\text{Friction term}}}$

Once again, there is no motion in the vertical direction, allowing us to set all opposing vertical forces equal to one another. These forces include the vertical component of the normal force pointing upwards and both the car's weight and the vertical component of friction pointing downwards:

${\displaystyle \underbrace {N\cos \theta =mg} _{\text{Frictionless formula}}+\underbrace {\mu _{s}N\sin \theta } _{\text{Friction term}}}$

By solving the above equation for mass and substituting this value into our previous equation we get:

${\displaystyle {\frac {{\frac {N\cos \theta -\mu _{s}N\sin \theta }{g}}v^{2}}{r}}=N\sin \theta +\mu _{s}N\cos \theta }$

Solving for ${\displaystyle v}$ we get:

${\displaystyle v_{\mathrm {max} }={\sqrt {rg\left(\sin \theta +\mu _{s}\cos \theta \right) \over \cos \theta -\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta +\mu _{s}}{1-\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta +\theta _{\mathrm {crit} })}}}$

Where ${\displaystyle \theta _{\mathrm {crit} }}$ is the critical angle, such that ${\displaystyle \tan \theta _{\mathrm {crit} }=\mu _{s}}$. This equation provides the maximum velocity for the automobile with the given angle of incline, coefficient of static friction and radius of curvature. By a similar analysis of minimum velocity, the following equation is rendered:

${\displaystyle v_{\mathrm {min} }={\sqrt {rg\left(\sin \theta -\mu _{s}\cos \theta \right) \over \cos \theta +\mu _{s}\sin \theta }}={\sqrt {rg{\frac {\tan \theta -\mu _{s}}{1+\mu _{s}\tan \theta }}}}={\sqrt {rg\tan(\theta -\theta _{\mathrm {crit} })}}}$

Notice

${\displaystyle {\frac {v_{\mathrm {min} }}{v_{\mathrm {max} }}}={\sqrt {\frac {\tan(\theta -\theta _{\mathrm {crit} })}{\tan(\theta +\theta _{\mathrm {crit} })}}}}$

The difference in the latter analysis comes when considering the direction of friction for the minimum velocity of the automobile (towards the outside of the circle). Consequently, opposite operations are performed when inserting friction into equations for forces in the centripetal and vertical directions.

Improperly banked road curves increase the risk of run-off-road and head-on crashes. A 2% deficiency in superelevation (say, 4% superelevation on a curve that should have 6%) can be expected to increase crash frequency by 6%, and a 5% deficiency will increase it by 15%. ^[3] Up until now, highway engineers have been without efficient tools to identify improperly banked curves and to design relevant mitigating road actions. A modern profilograph can provide data of both road curvature and cross slope (angle of incline). A practical demonstration of how to evaluate improperly banked turns was developed in the EU Roadex III project. See the linked referenced document below.

Banked turn in aeronautics

When a fixed-wing aircraft is making a turn (changing its direction) the aircraft must roll to a banked position so that its wings are angled towards the desired direction of the turn. When the turn has been completed the aircraft must roll back to the wings-level position in order to resume straight flight. ^[4]

When any moving vehicle is making a turn, it is necessary for the forces acting on the vehicle to add up to a net inward force, to cause centripetal acceleration. In the case of an aircraft making a turn, the force causing centripetal acceleration is the horizontal component of the lift acting on the aircraft.

In straight, level flight, the lift acting on the aircraft acts vertically upwards to counteract the weight of the aircraft which acts downwards. If the aircraft is to continue in level flight (i.e. at constant altitude), the vertical component must continue to equal the weight of the aircraft and so the pilot must pull back on the stick to apply the elevators to pitch the nose up, and therefore increase the angle of attack, generating an increase in the lift of the wing. The total (now angled) lift is greater than the weight of the aircraft, The excess lift is the horizontal component of the total lift, which is the net force causing the aircraft to accelerate inward and execute the turn.

Because centripetal acceleration is:

${\displaystyle a={v^{2} \over r}}$

During a balanced turn where the angle of bank is ${\displaystyle \theta }$ the lift acts at an angle ${\displaystyle \theta }$ away from the vertical. It is useful to resolve the lift into a vertical component and a horizontal component.

Newton's second law in the horizontal direction can be expressed mathematically as:

${\displaystyle L\sin \theta ={mv^{2} \over r}}$

where:

${\displaystyle L}$ is the lift acting on the aircraft

${\displaystyle \theta }$ is the angle of bank of the aircraft

${\displaystyle m}$ is the mass of the aircraft

${\displaystyle v}$ is the true airspeed of the aircraft

${\displaystyle r}$ is the radius of the turn

In straight level flight, lift is equal to the aircraft weight. In turning flight the lift exceeds the aircraft weight, and is equal to the weight of the aircraft (${\displaystyle g}$) divided by the cosine of the angle of bank:

${\displaystyle L={mg \over {\cos \theta }}}$

where ${\displaystyle g}$ is the gravitational field strength.

The radius of the turn can now be calculated: ^[5]

${\displaystyle r={v^{2} \over {g\tan \theta }}}$

This formula shows that the radius of turn is proportional to the square of the aircraft's true airspeed. With a higher airspeed the radius of turn is larger, and with a lower airspeed the radius is smaller.

This formula also shows that the radius of turn decreases with the angle of bank. With a higher angle of bank the radius of turn is smaller, and with a lower angle of bank the radius is greater.

In a banked turn at constant altitude, the load factor is equal to ${\displaystyle {\frac {1}{\cos \theta }}}$. We can see that the load factor in straight and level flight is ${\displaystyle 1}$, since ${\displaystyle \cos(0)=1}$, and to generate sufficient lift to maintain constant altitude, the load factor must approach infinity as the bank angle approaches ${\displaystyle 90^{\circ }}$ and ${\displaystyle \cos \theta }$ approaches ${\displaystyle 0}$. This is physically impossible, because structural limitations of the aircraft or physical endurance of the occupants will be exceeded well before then.

Banked turn in athletics

Most indoor track and field venues have banked turns since the tracks are smaller than outdoor tracks. The tight turns on these small tracks are usually banked to allow athletes to lean inward and neutralize the centrifugal force as they race around the curve; the lean is especially noticeable on sprint events. ^[6]

• 
  Sprinters leaning into a turn on a banked indoor track

See also

Related Research Articles

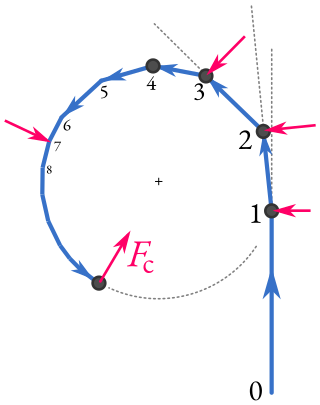
A centripetal force is a force that makes a body follow a curved path. The direction of the centripetal force is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. Isaac Newton described it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits.

In particle physics, the electroweak interaction or electroweak force is the unified description of two of the four known fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single force. Thus, if the temperature is high enough – approximately 10¹⁵ K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 10¹⁵ K has not been seen widely throughout the universe since before the quark epoch, and currently the highest human-made temperature in thermal equilibrium is around 5.5×10¹² K (from the Large Hadron Collider).

The Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by French engineer and physicist Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, when no one realized that the waves were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.

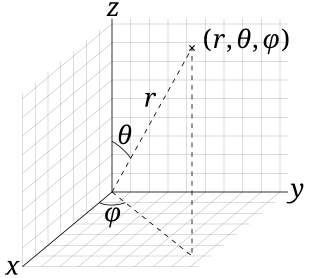
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

An inclined plane, also known as a ramp, is a flat supporting surface tilted at an angle from the vertical direction, with one end higher than the other, used as an aid for raising or lowering a load. The inclined plane is one of the six classical simple machines defined by Renaissance scientists. Inclined planes are used to move heavy loads over vertical obstacles. Examples vary from a ramp used to load goods into a truck, to a person walking up a pedestrian ramp, to an automobile or railroad train climbing a grade.

Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of gravity (cg), known as pitch, roll and yaw. These are collectively known as aircraft attitude, often principally relative to the atmospheric frame in normal flight, but also relative to terrain during takeoff or landing, or when operating at low elevation. The concept of attitude is not specific to fixed-wing aircraft, but also extends to rotary aircraft such as helicopters, and dirigibles, where the flight dynamics involved in establishing and controlling attitude are entirely different.

A sub-orbital spaceflight is a spaceflight in which the spacecraft reaches outer space, but its trajectory intersects the surface of the gravitating body from which it was launched. Hence, it will not complete one orbital revolution, will not become an artificial satellite nor will it reach escape velocity.

The angle of repose, or critical angle of repose, of a granular material is the steepest angle of descent or dip relative to the horizontal plane on which the material can be piled without slumping. At this angle, the material on the slope face is on the verge of sliding. The angle of repose can range from 0° to 90°. The morphology of the material affects the angle of repose; smooth, rounded sand grains cannot be piled as steeply as can rough, interlocking sands. The angle of repose can also be affected by additions of solvents. If a small amount of water is able to bridge the gaps between particles, electrostatic attraction of the water to mineral surfaces increases the angle of repose, and related quantities such as the soil strength.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible.

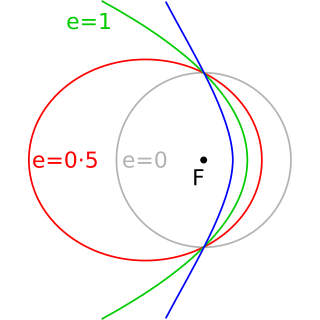
In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.

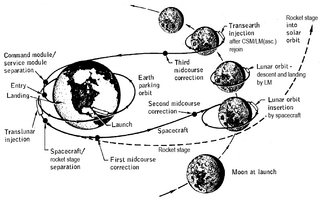
Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles of the sphere. Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.

A conical pendulum consists of a weight fixed on the end of a string or rod suspended from a pivot. Its construction is similar to an ordinary pendulum; however, instead of swinging back and forth along a circular arc, the bob of a conical pendulum moves at a constant speed in a circle or ellipse with the string tracing out a cone. The conical pendulum was first studied by the English scientist Robert Hooke around 1660 as a model for the orbital motion of planets. In 1673 Dutch scientist Christiaan Huygens calculated its period, using his new concept of centrifugal force in his book Horologium Oscillatorium. Later it was used as the timekeeping element in a few mechanical clocks and other clockwork timing devices.

A pendulum is a body suspended from a fixed support such that it freely swings back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.

There are several equivalent ways for defining trigonometric functions, and the proofs of the trigonometric identities between them depend on the chosen definition. The oldest and most elementary definitions are based on the geometry of right triangles. The proofs given in this article use these definitions, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

Sliding is a type of motion between two surfaces in contact. This can be contrasted to rolling motion. Both types of motion may occur in bearings.

The capstan equation or belt friction equation, also known as Euler-Eytelwein formula, relates the hold-force to the load-force if a flexible line is wound around a cylinder.

In optics, polarization mixing refers to changes in the relative strengths of the Stokes parameters caused by reflection or scattering—see vector radiative transfer—or by changes in the radial orientation of the detector.

In statistics, the Behrens–Fisher distribution, named after Ronald Fisher and Walter Behrens, is a parameterized family of probability distributions arising from the solution of the Behrens–Fisher problem proposed first by Behrens and several years later by Fisher. The Behrens–Fisher problem is that of statistical inference concerning the difference between the means of two normally distributed populations when the ratio of their variances is not known.

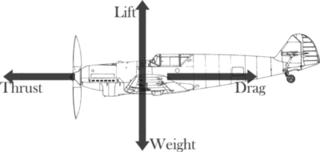
Steady flight, unaccelerated flight, or equilibrium flight is a special case in flight dynamics where the aircraft's linear and angular velocity are constant in a body-fixed reference frame. Basic aircraft maneuvers such as level flight, climbs and descents, and coordinated turns can be modeled as steady flight maneuvers. Typical aircraft flight consists of a series of steady flight maneuvers connected by brief, accelerated transitions. Because of this, primary applications of steady flight models include aircraft design, assessment of aircraft performance, flight planning, and using steady flight states as the equilibrium conditions around which flight dynamics equations are expanded.

References

Further reading

Surface vehicles

• Serway, Raymond. Physics for Scientists and Engineers. Cengage Learning, 2010.
• Health and Safety Issues, the EU Roadex III project on health and safety issues raised by poorly maintained road networks.

Aeronautics

• Kermode, A.C. (1972) Mechanics of Flight, Chapter 8, 10th Edition, Longman Group Limited, London ISBN   0-582-23740-8
• Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London ISBN   0-273-01120-0
• Hurt, H.H. Jr, (1960), Aerodynamics for Naval Aviators, A National Flightshop Reprint, Florida

External links

Surface vehicles

• http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/carbank.gif
• https://web.archive.org/web/20051222173550/http://whitts.alioth.net/
• http://www.batesville.k12.in.us/physics/PHYNET/Mechanics/Circular%20Motion/banked_no_friction.htm

Aeronautics

• NASA: Guidance on banking turns
• aerospaceweb.org: Bank Angle and G's (math)
• Pilot’s Handbook of Aeronautical Knowledge

https://edu-physics.com/2021/05/08/how-banking-of-road-will-help-the-vehicle-to-travel-along-a-circular-path-2/