Alternating decision tree

An alternating decision tree (ADTree) is a machine learning method for classification. It generalizes decision trees and has connections to boosting.

Contents

• History
• Motivation
• Alternating decision tree structure
• Example
• Description of the algorithm
• Empirical results
• References
• External links

An ADTree consists of an alternation of decision nodes, which specify a predicate condition, and prediction nodes, which contain a single number. An instance is classified by an ADTree by following all paths for which all decision nodes are true, and summing any prediction nodes that are traversed.

History

ADTrees were introduced by Yoav Freund and Llew Mason. ^[1] However, the algorithm as presented had several typographical errors. Clarifications and optimizations were later presented by Bernhard Pfahringer, Geoffrey Holmes and Richard Kirkby. ^[2] Implementations are available in Weka and JBoost.

Motivation

Original boosting algorithms typically used either decision stumps or decision trees as weak hypotheses. As an example, boosting decision stumps creates a set of ${\displaystyle T}$ weighted decision stumps (where ${\displaystyle T}$ is the number of boosting iterations), which then vote on the final classification according to their weights. Individual decision stumps are weighted according to their ability to classify the data.

Boosting a simple learner results in an unstructured set of ${\displaystyle T}$ hypotheses, making it difficult to infer correlations between attributes. Alternating decision trees introduce structure to the set of hypotheses by requiring that they build off a hypothesis that was produced in an earlier iteration. The resulting set of hypotheses can be visualized in a tree based on the relationship between a hypothesis and its "parent."

Another important feature of boosted algorithms is that the data is given a different distribution at each iteration. Instances that are misclassified are given a larger weight while accurately classified instances are given reduced weight.

Alternating decision tree structure

An alternating decision tree consists of decision nodes and prediction nodes. Decision nodes specify a predicate condition. Prediction nodes contain a single number. ADTrees always have prediction nodes as both root and leaves. An instance is classified by an ADTree by following all paths for which all decision nodes are true and summing any prediction nodes that are traversed. This is different from binary classification trees such as CART (Classification and regression tree) or C4.5 in which an instance follows only one path through the tree.

Example

The following tree was constructed using JBoost on the spambase dataset ^[3] (available from the UCI Machine Learning Repository). ^[4] In this example, spam is coded as 1 and regular email is coded as −1.

The following table contains part of the information for a single instance.

An instance to be classified

Feature	Value
char_freq_bang	0.08
word_freq_hp	0.4
capital_run_length_longest	4
char_freq_dollar	0
word_freq_remove	0.9
word_freq_george	0
Other features	...

The instance is scored by summing all of the prediction nodes through which it passes. In the case of the instance above, the score is calculated as

Score for the above instance

Iteration	0	1	2	3	4	5	6
Instance values	—	.08 < .052 = f	.4 < .195 = f	0 < .01 = t	0 < 0.005 = t	—	.9 < .225 = f
Prediction	-0.093	0.74	-1.446	-0.38	0.176	0	1.66

The final score of 0.657 is positive, so the instance is classified as spam. The magnitude of the value is a measure of confidence in the prediction. The original authors list three potential levels of interpretation for the set of attributes identified by an ADTree:

• Individual nodes can be evaluated for their own predictive ability.
• Sets of nodes on the same path may be interpreted as having a joint effect
• The tree can be interpreted as a whole.

Care must be taken when interpreting individual nodes as the scores reflect a re weighting of the data in each iteration.

Description of the algorithm

The inputs to the alternating decision tree algorithm are:

• A set of inputs ${\displaystyle (x_{1},y_{1}),\ldots ,(x_{m},y_{m})}$ where ${\displaystyle x_{i}}$ is a vector of attributes and ${\displaystyle y_{i}}$ is either -1 or 1. Inputs are also called instances.
• A set of weights ${\displaystyle w_{i}}$ corresponding to each instance.

The fundamental element of the ADTree algorithm is the rule. A single rule consists of a precondition, a condition, and two scores. A condition is a predicate of the form "attribute <comparison> value." A precondition is simply a logical conjunction of conditions. Evaluation of a rule involves a pair of nested if statements:

1  if (precondition) 2      if (condition) 3          return score_one 4      else 5          return score_two 6      end if 7  else 8      return 0 9  end if

Several auxiliary functions are also required by the algorithm:

• ${\displaystyle W_{+}(c)}$ returns the sum of the weights of all positively labeled examples that satisfy predicate ${\displaystyle c}$
• ${\displaystyle W_{-}(c)}$ returns the sum of the weights of all negatively labeled examples that satisfy predicate ${\displaystyle c}$
• ${\displaystyle W(c)=W_{+}(c)+W_{-}(c)}$ returns the sum of the weights of all examples that satisfy predicate ${\displaystyle c}$

The algorithm is as follows:

1  function ad_tree 2  input Set of m training instances 3  4  wi = 1/m for all i 5  ${\displaystyle a={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(true)}{W_{-}(true)}}}$ 6  R0 = a rule with scores a and 0, precondition "true" and condition "true." 7  ${\displaystyle {\mathcal {P}}=\{true\}}$ 8  ${\displaystyle {\mathcal {C}}=}$ the set of all possible conditions 9  for${\displaystyle j=1\dots T}$ 10      ${\displaystyle p\in {\mathcal {P}},c\in {\mathcal {C}}}$ get valuesthat minimize ${\displaystyle z=2\left({\sqrt {W_{+}(p\wedge c)W_{-}(p\wedge c)}}+{\sqrt {W_{+}(p\wedge \neg c)W_{-}(p\wedge \neg c)}}\right)+W(\neg p)}$ 11      ${\displaystyle {\mathcal {P}}+=p\wedge c+p\wedge \neg c}$ 12      ${\displaystyle a_{1}={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(p\wedge c)+1}{W_{-}(p\wedge c)+1}}}$ 13      ${\displaystyle a_{2}={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(p\wedge \neg c)+1}{W_{-}(p\wedge \neg c)+1}}}$ 14      Rj = new rule with precondition p, condition c, and weights a1 and a2 15      ${\displaystyle w_{i}=w_{i}e^{-y_{i}R_{j}(x_{i})}}$ 16  end for 17  return set of Rj

The set ${\displaystyle {\mathcal {P}}}$ grows by two preconditions in each iteration, and it is possible to derive the tree structure of a set of rules by making note of the precondition that is used in each successive rule.

Empirical results

Figure 6 in the original paper ^[1] demonstrates that ADTrees are typically as robust as boosted decision trees and boosted decision stumps. Typically, equivalent accuracy can be achieved with a much simpler tree structure than recursive partitioning algorithms.

Related Research Articles

Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions.

In statistics, naive Bayes classifiers are a family of simple "probabilistic classifiers" based on applying Bayes' theorem with strong (naive) independence assumptions between the features. They are among the simplest Bayesian network models, but coupled with kernel density estimation, they can achieve high accuracy levels.

Hoare logic is a formal system with a set of logical rules for reasoning rigorously about the correctness of computer programs. It was proposed in 1969 by the British computer scientist and logician Tony Hoare, and subsequently refined by Hoare and other researchers. The original ideas were seeded by the work of Robert W. Floyd, who had published a similar system for flowcharts.

Decision tree learning is a supervised learning approach used in statistics, data mining and machine learning. In this formalism, a classification or regression decision tree is used as a predictive model to draw conclusions about a set of observations.

The set cover problem is a classical question in combinatorics, computer science, operations research, and complexity theory. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972.

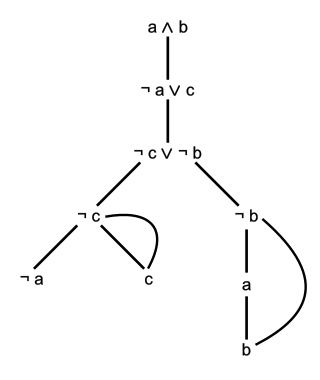
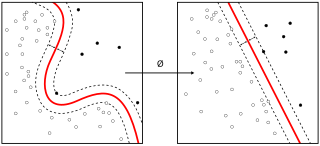
In proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.

Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned. Random decision forests correct for decision trees' habit of overfitting to their training set. Random forests generally outperform decision trees, but their accuracy is lower than gradient boosted trees. However, data characteristics can affect their performance.

Predicate transformer semantics were introduced by Edsger Dijkstra in his seminal paper "Guarded commands, nondeterminacy and formal derivation of programs". They define the semantics of an imperative programming paradigm by assigning to each statement in this language a corresponding predicate transformer: a total function between two predicates on the state space of the statement. In this sense, predicate transformer semantics are a kind of denotational semantics. Actually, in guarded commands, Dijkstra uses only one kind of predicate transformer: the well-known weakest preconditions.

AdaBoost, short for Adaptive Boosting, is a statistical classification meta-algorithm formulated by Yoav Freund and Robert Schapire in 1995, who won the 2003 Gödel Prize for their work. It can be used in conjunction with many other types of learning algorithms to improve performance. The output of the other learning algorithms is combined into a weighted sum that represents the final output of the boosted classifier. Usually, AdaBoost is presented for binary classification, although it can be generalized to multiple classes or bounded intervals on the real line.

In statistics, the k-nearest neighbors algorithm (k-NN) is a non-parametric supervised learning method first developed by Evelyn Fix and Joseph Hodges in 1951, and later expanded by Thomas Cover. It is used for classification and regression. In both cases, the input consists of the k closest training examples in a data set. The output depends on whether k-NN is used for classification or regression:

A multilayer perceptron (MLP) is a fully connected class of feedforward artificial neural network (ANN). The term MLP is used ambiguously, sometimes loosely to mean any feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons ; see § Terminology. Multilayer perceptrons are sometimes colloquially referred to as "vanilla" neural networks, especially when they have a single hidden layer.

Answer set programming (ASP) is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers—programs for generating stable models—are used to perform search. The computational process employed in the design of many answer set solvers is an enhancement of the DPLL algorithm and, in principle, it always terminates.

In decision theory, a scoring rule provides a summary measure for the evaluation of probabilistic predictions or forecasts. It is applicable to tasks in which predictions assign probabilities to events, i.e. one issues a probability distribution as prediction. This includes probabilistic classification of a set of mutually exclusive outcomes or classes.

Linear Programming Boosting (LPBoost) is a supervised classifier from the boosting family of classifiers. LPBoost maximizes a margin between training samples of different classes and hence also belongs to the class of margin-maximizing supervised classification algorithms. Consider a classification function

BrownBoost is a boosting algorithm that may be robust to noisy datasets. BrownBoost is an adaptive version of the boost by majority algorithm. As is true for all boosting algorithms, BrownBoost is used in conjunction with other machine learning methods. BrownBoost was introduced by Yoav Freund in 2001.

In computer science and graph theory, Karger's algorithm is a randomized algorithm to compute a minimum cut of a connected graph. It was invented by David Karger and first published in 1993.

Gradient boosting is a machine learning technique used in regression and classification tasks, among others. It gives a prediction model in the form of an ensemble of weak prediction models, which are typically decision trees. When a decision tree is the weak learner, the resulting algorithm is called gradient-boosted trees; it usually outperforms random forest. A gradient-boosted trees model is built in a stage-wise fashion as in other boosting methods, but it generalizes the other methods by allowing optimization of an arbitrary differentiable loss function.

The Boolean satisfiability problem can be stated formally as: given a Boolean expression with variables, finding an assignment of the variables such that is true. It is seen as the canonical NP-complete problem. While no efficient algorithm is known to solve this problem in the general case, there are certain heuristics, informally called 'rules of thumb' in programming, that can usually help solve the problem reasonably efficiently.

In machine learning, multiple-instance learning (MIL) is a type of supervised learning. Instead of receiving a set of instances which are individually labeled, the learner receives a set of labeled bags, each containing many instances. In the simple case of multiple-instance binary classification, a bag may be labeled negative if all the instances in it are negative. On the other hand, a bag is labeled positive if there is at least one instance in it which is positive. From a collection of labeled bags, the learner tries to either (i) induce a concept that will label individual instances correctly or (ii) learn how to label bags without inducing the concept.

The multiplicative weights update method is an algorithmic technique most commonly used for decision making and prediction, and also widely deployed in game theory and algorithm design. The simplest use case is the problem of prediction from expert advice, in which a decision maker needs to iteratively decide on an expert whose advice to follow. The method assigns initial weights to the experts, and updates these weights multiplicatively and iteratively according to the feedback of how well an expert performed: reducing it in case of poor performance, and increasing it otherwise. It was discovered repeatedly in very diverse fields such as machine learning, optimization, theoretical computer science, and game theory.

References

External links

• An introduction to Boosting and ADTrees (Has many graphical examples of alternating decision trees in practice).
• JBoost software implementing ADTrees.