JP2005091660A - Anamorphic optical system - Google Patents
Anamorphic optical system Download PDFInfo
- Publication number
- JP2005091660A JP2005091660A JP2003324072A JP2003324072A JP2005091660A JP 2005091660 A JP2005091660 A JP 2005091660A JP 2003324072 A JP2003324072 A JP 2003324072A JP 2003324072 A JP2003324072 A JP 2003324072A JP 2005091660 A JP2005091660 A JP 2005091660A
- Authority
- JP
- Japan
- Prior art keywords
- optical system
- anamorphic
- axis direction
- lenses
- lens
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Pending
Links
Images
Landscapes
- Microscoopes, Condenser (AREA)
- Lenses (AREA)
Abstract
Description
本発明はアナモフィック光学系に関するものであり、特に、安価で高性能・高アナモ比のアナモフィック光学系、並びにそれを有する照明光学系及び照明装置に関するものである。 The present invention relates to an anamorphic optical system, and more particularly to an inexpensive anamorphic optical system having high performance and a high anamorphic ratio, and an illumination optical system and an illumination apparatus having the anamorphic optical system.
アナモフィック光学系は様々な分野で利用されており、例えば、縦横の拡大率を変えた像の観察、矩形形状の物体面や光学素子面(例えば表示素子面)に対する効率的な照明等に用いられている。このため、従来より提案されているアナモフィック光学系のタイプも様々であり(例えば、特許文献1,2参照。)、回転対称光学系を含んだタイプのアナモフィック光学系も提案されている(例えば、特許文献3参照。)。
ここで、アナモフィック光学系で矩形形状の物体面を照明する場合を考えてみる。光源からの光を楕円面鏡で集光したときの光束の断面形状は、円形又は楕円形である。このため、そこからそのまま矩形形状に光束を切り出したのでは、矩形形状の物体面を効率良く照明することができない。特に、矩形形状の縦横比が大きければ、なおさらその傾向は強くなる。使用するアナモフィック光学系を、矩形形状の短辺方向には縮小倍率(又は等倍より低い拡大倍率)とし、矩形形状の長辺方向には大きな拡大倍率とすれば、円形の光束からの光の利用効率を高くすることができる。 Here, consider a case where a rectangular object surface is illuminated by an anamorphic optical system. The cross-sectional shape of the light beam when the light from the light source is collected by the ellipsoidal mirror is circular or elliptical. For this reason, if the light beam is cut out into a rectangular shape as it is, the rectangular object surface cannot be efficiently illuminated. In particular, the tendency becomes stronger if the aspect ratio of the rectangular shape is large. If the anamorphic optical system to be used has a reduction magnification (or an enlargement magnification lower than the same magnification) in the short side direction of the rectangular shape and a large enlargement magnification in the long side direction of the rectangular shape, the light from the circular light beam Utilization efficiency can be increased.
しかしながら、特許文献1〜3で提案されているような従来のアナモフィック光学系では、この縦横の拡大率の比(すなわちアナモ比)があまり大きくないため、縦横比の非常に大きな物体面や光学素子面の照明には対応することができない。さらに、縦横の大きさの比が大きく歪んだ像を元の歪みのない像として観察する場合、逆に像の縦横の大きさの比を大きく歪ませて観察する場合には、従来のアナモフィック光学系では対応することができない。また、単純にアナモ比を大きくしようとすると、同等のレンズ枚数では性能が著しく低下してしまい、逆に、アナモ比が大きく高性能なアナモフィック光学系を実現しようとすると、レンズ枚数が極端に多くなってしまう。そしてレンズ枚数が多くなると、アナモフィック光学系は非常に高価なものとなり、さらに全長が大きくなってコンパクト化が困難になる。 However, in the conventional anamorphic optical systems proposed in Patent Documents 1 to 3, since the ratio of the aspect ratio (that is, the anamorphic ratio) is not so large, an object surface or an optical element having a very large aspect ratio. It cannot cope with surface illumination. Furthermore, when observing a distorted image with a large vertical / horizontal ratio as an original image without distortion, or conversely when observing with a large distortion of the vertical / horizontal ratio, the conventional anamorphic optics The system cannot handle it. Also, simply trying to increase the anamorphic ratio results in a significant decrease in performance with the same number of lenses, and conversely, when trying to realize a high-performance anamorphic optical system with a large anamorphic ratio, the number of lenses is extremely large. turn into. If the number of lenses increases, the anamorphic optical system becomes very expensive, and the overall length becomes larger, making it difficult to make the system compact.
本発明はこのような状況に鑑みてなされたものであって、その目的は、少ないレンズ枚数で高い光学性能を保持しながら、大きなアナモ比を有するアナモフィック光学系を提供することにある。 The present invention has been made in view of such circumstances, and an object thereof is to provide an anamorphic optical system having a large anamorphic ratio while maintaining high optical performance with a small number of lenses.
上記目的を達成するために、第1の発明のアナモフィック光学系は、光軸に対して回転対称な回転対称レンズと、互いに垂直な方向の曲率が異なる面を含むアナモフィックレンズと、をそれぞれ1枚以上有するとともに、互いに垂直な方向の倍率が異なるアナモフィック光学系であって、倍率の絶対値の大きい方向を長軸方向、倍率の絶対値の小さい方向を短軸方向とするとき、以下の条件式(1)を満足することを特徴とする。 In order to achieve the above object, an anamorphic optical system according to a first invention includes a rotationally symmetric lens rotationally symmetric with respect to an optical axis and an anamorphic lens including surfaces having different curvatures in directions perpendicular to each other. An anamorphic optical system having the above and different magnifications in directions perpendicular to each other, where the direction of large absolute value of the magnification is the major axis direction and the direction of small absolute value of the magnification is the minor axis direction, the following conditional expression It is characterized by satisfying (1).
1.90<|fXall/fsym|<20.00 …(1)
ただし、
fXall:アナモフィック光学系の長軸方向の焦点距離、
fsym:全回転対称レンズのみから成るレンズ群の焦点距離、
である。
1.90 <| fXall / fsym | <20.00… (1)
However,
fXall: Focal length in the long axis direction of the anamorphic optical system,
fsym: focal length of a lens group consisting only of all rotationally symmetric lenses,
It is.
第2の発明のアナモフィック光学系は、上記第1の発明において、以下の条件式(2)を満足することを特徴とする。 The anamorphic optical system of the second invention is characterized in that, in the first invention, the following conditional expression (2) is satisfied.
6.4<|βlong/βshort|<30.0 …(2)
ただし、
βlong:アナモフィック光学系の長軸方向の倍率、
βshort:アナモフィック光学系の短軸方向の倍率、
である。
6.4 <| βlong / βshort | <30.0 (2)
However,
βlong: magnification in the long axis direction of the anamorphic optical system,
βshort: magnification in the minor axis direction of the anamorphic optical system,
It is.
第3の発明のアナモフィック光学系は、光軸に対して回転対称な回転対称レンズと、互いに垂直な方向の曲率が異なる面を含むアナモフィックレンズと、をそれぞれ1枚以上有するとともに、互いに垂直な方向の倍率が異なるアナモフィック光学系であって、倍率の絶対値の大きい方向を長軸方向、倍率の絶対値の小さい方向を短軸方向とするとき、以下の条件式(2)を満足することを特徴とする。 An anamorphic optical system according to a third aspect of the present invention has at least one rotationally symmetric lens that is rotationally symmetric with respect to the optical axis and one or more anamorphic lenses that include surfaces having different curvatures in directions perpendicular to each other, and directions perpendicular to each other. When the anamorphic optical system has different magnifications, the major axis direction is the direction where the absolute value of the magnification is larger, and the minor axis direction is the direction where the absolute value of the magnification is smaller.The following conditional expression (2) is satisfied: Features.
6.4<|βlong/βshort|<30.0 …(2)
ただし、
βlong:アナモフィック光学系の長軸方向の倍率、
βshort:アナモフィック光学系の短軸方向の倍率、
である。
6.4 <| βlong / βshort | <30.0 (2)
However,
βlong: magnification in the long axis direction of the anamorphic optical system,
βshort: magnification in the minor axis direction of the anamorphic optical system,
It is.
第4の発明のアナモフィック光学系は、上記第3の発明において、以下の条件式(1)を満足することを特徴とする。 An anamorphic optical system according to a fourth invention is characterized in that, in the third invention, the following conditional expression (1) is satisfied.
1.90<|fXall/fsym|<20.00 …(1)
ただし、
fXall:アナモフィック光学系の長軸方向の焦点距離、
fsym:全回転対称レンズのみから成るレンズ群の焦点距離、
である。
1.90 <| fXall / fsym | <20.00… (1)
However,
fXall: Focal length in the long axis direction of the anamorphic optical system,
fsym: focal length of a lens group consisting only of all rotationally symmetric lenses,
It is.
第5の発明の照明光学系は、光源からの光を被照射面に導く照明光学系であって、前記光源が第1焦点近傍に位置するように配置された楕円面鏡と、その楕円面鏡の第2焦点近傍に入射端面を持つオプティカルインテグレータと、そのオプティカルインテグレータの射出端面の像を被照射面上に形成する結像光学系とを有し、前記結像光学系が上記第1〜第4のいずれか1つの発明に係るアナモフィック光学系から成ることを特徴とする。 An illumination optical system according to a fifth aspect of the present invention is an illumination optical system that guides light from a light source to an irradiated surface, the ellipsoidal mirror disposed so that the light source is located in the vicinity of the first focal point, and the elliptical surface thereof. An optical integrator having an incident end face in the vicinity of the second focal point of the mirror, and an imaging optical system for forming an image of the exit end face of the optical integrator on the irradiated surface. It comprises an anamorphic optical system according to any one of the fourth inventions.
第6の発明の照明装置は、楕円面鏡と、その楕円面鏡の第1焦点近傍に配置された光源と、前記楕円面鏡の第2焦点近傍に入射端面を持つオプティカルインテグレータと、そのオプティカルインテグレータの射出端面の像を被照射面上に形成する結像光学系とを有し、前記結像光学系が上記第1〜第4のいずれか1つの発明に係るアナモフィック光学系から成ることを特徴とする。 An illumination device according to a sixth aspect of the present invention includes an ellipsoidal mirror, a light source disposed near the first focal point of the ellipsoidal mirror, an optical integrator having an incident end surface near the second focal point of the ellipsoidal mirror, and an optical device thereof. An imaging optical system that forms an image of the exit end face of the integrator on the irradiated surface, and the imaging optical system comprises the anamorphic optical system according to any one of the first to fourth inventions. Features.
本発明によれば、回転対称レンズとアナモフィックレンズを共に有する特徴的な光学構成になっているため、少ないレンズ枚数で高い光学性能を保持しながら、大きなアナモ比を有する安価なアナモフィック光学系を実現することができる。そして、本発明に係るアナモフィック光学系を用いて照明光学系や照明装置を構成すれば、これらの軽量・コンパクト化,低コスト化,高性能化,光利用効率の向上等に寄与することができる。 According to the present invention, since it has a characteristic optical configuration having both a rotationally symmetric lens and an anamorphic lens, it realizes an inexpensive anamorphic optical system having a large anamorphic ratio while maintaining high optical performance with a small number of lenses. can do. If an illuminating optical system or an illuminating device is configured using the anamorphic optical system according to the present invention, it is possible to contribute to such lightness, compactness, low cost, high performance, and improvement of light utilization efficiency. .
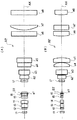
以下、本発明を実施したアナモフィック光学系等を、図面を参照しつつ説明する。図1〜図4に、アナモフィック光学系の第1〜第4の実施の形態のレンズ構成をそれぞれ光学断面で示す。図1〜図4において、(A)は長軸方向(すなわち倍率の絶対値の大きい方向)のレンズ構成、(B)は短軸方向(すなわち倍率の絶対値の小さい方向)のレンズ構成をそれぞれ示しており、APは互いに垂直な方向(つまり長軸方向と短軸方向)の倍率が異なるアナモフィック光学系、ti(i=1,2,3,...)は光軸AXに対して回転対称な第i回転対称レンズ、aj(j=1,2,3,...)は互いに垂直な方向の曲率が異なる面を含む第jアナモフィックレンズ、STは絞り、SXは長軸方向絞り、SYは短軸方向絞りをそれぞれ示している。 Hereinafter, an anamorphic optical system and the like embodying the present invention will be described with reference to the drawings. 1 to 4 show the lens configurations of the first to fourth embodiments of the anamorphic optical system in optical sections, respectively. 1 to 4, (A) shows the lens configuration in the major axis direction (that is, the direction in which the absolute value of the magnification is large), and (B) shows the lens configuration in the minor axis direction (that is, the direction in which the absolute value of the magnification is small). In the figure, AP is an anamorphic optical system having different magnifications in directions perpendicular to each other (that is, the major axis direction and the minor axis direction), and ti (i = 1, 2, 3,...) Rotates with respect to the optical axis AX. Symmetric i-th rotationally symmetric lens, aj (j = 1, 2, 3,...) Is a jth anamorphic lens including surfaces having different curvatures in directions perpendicular to each other, ST is a stop, SX is a long-axis direction stop, SY indicates a short-axis direction stop, respectively.
第1の実施の形態(図1)のアナモフィック光学系APは、長軸方向の縮小側から順に、第1〜第4回転対称レンズt1〜t4と、第1,第2アナモフィックレンズa1,a2と、長軸方向絞りSXと、第3〜第5アナモフィックレンズa3〜a5と、短軸方向絞りSYと、第6〜第10アナモフィックレンズa6〜a10と、から成っている。第1回転対称レンズt1は正パワーを有する平凸レンズであり、第2回転対称レンズt2は負パワーを有する平凹レンズであり、第3,第4回転対称レンズt3,t4は正パワーを有する平凸レンズである。第1アナモフィックレンズa1は長軸方向に負パワーを有するシリンドリカルレンズであり、第2〜第4アナモフィックレンズa2〜a4は長軸方向に正パワーを有するシリンドリカルレンズであり、第5,第6アナモフィックレンズa5,a6は短軸方向に正パワーを有するシリンドリカルレンズであり、第7アナモフィックレンズa7は短軸方向に負パワーを有するシリンドリカルレンズであり、第8〜第10アナモフィックレンズa8〜a10は短軸方向に正パワーを有するシリンドリカルレンズである。 The anamorphic optical system AP of the first embodiment (FIG. 1) includes, in order from the reduction side in the long axis direction, first to fourth rotationally symmetric lenses t1 to t4, first and second anamorphic lenses a1 and a2. And a long axis direction diaphragm SX, third to fifth anamorphic lenses a3 to a5, a short axis direction diaphragm SY, and sixth to tenth anamorphic lenses a6 to a10. The first rotationally symmetric lens t1 is a planoconvex lens having positive power, the second rotationally symmetric lens t2 is a planoconcave lens having negative power, and the third and fourth rotationally symmetric lenses t3 and t4 are planoconvex lenses having positive power. It is. The first anamorphic lens a1 is a cylindrical lens having negative power in the major axis direction, and the second to fourth anamorphic lenses a2 to a4 are cylindrical lenses having positive power in the major axis direction, and the fifth and sixth anamorphic lenses. a5 and a6 are cylindrical lenses having positive power in the minor axis direction, the seventh anamorphic lens a7 is a cylindrical lens having negative power in the minor axis direction, and the eighth to tenth anamorphic lenses a8 to a10 are in the minor axis direction. Is a cylindrical lens having positive power.
第2の実施の形態(図2)のアナモフィック光学系APは、長軸方向の縮小側から順に、第1〜第6回転対称レンズt1〜t6と、絞りSTと、第1アナモフィックレンズa1と、第7回転対称レンズt7と、第2〜第8アナモフィックレンズa2〜a8と、から成っている。第1回転対称レンズt1は負パワーを有するメニスカスレンズであり、第2回転対称レンズt2は負パワーを有する両凹レンズであり、第3〜第6回転対称レンズt3〜t6は正パワーを有する平凸レンズであり、第7回転対称レンズt7は負パワーを有するメニスカスレンズである。第1アナモフィックレンズa1は短軸方向に負パワーを有するシリンドリカルレンズであり、第2,第3アナモフィックレンズa2,a3は長軸方向に正パワーを有するシリンドリカルレンズであり、第4〜第6アナモフィックレンズa4〜a6は短軸方向に正パワーを有するシリンドリカルレンズであり、第7アナモフィックレンズa7は長軸方向に正パワーを有するシリンドリカルレンズであり、第8アナモフィックレンズa8は短軸方向に正パワーを有するシリンドリカルレンズである。 The anamorphic optical system AP of the second embodiment (FIG. 2) includes, in order from the reduction side in the long axis direction, first to sixth rotationally symmetric lenses t1 to t6, a diaphragm ST, a first anamorphic lens a1, The lens includes a seventh rotationally symmetric lens t7 and second to eighth anamorphic lenses a2 to a8. The first rotationally symmetric lens t1 is a meniscus lens having negative power, the second rotationally symmetric lens t2 is a biconcave lens having negative power, and the third to sixth rotationally symmetric lenses t3 to t6 are planoconvex lenses having positive power. The seventh rotationally symmetric lens t7 is a meniscus lens having negative power. The first anamorphic lens a1 is a cylindrical lens having negative power in the minor axis direction, the second and third anamorphic lenses a2 and a3 are cylindrical lenses having positive power in the major axis direction, and the fourth to sixth anamorphic lenses. a4 to a6 are cylindrical lenses having positive power in the minor axis direction, the seventh anamorphic lens a7 is a cylindrical lens having positive power in the major axis direction, and the eighth anamorphic lens a8 has positive power in the minor axis direction. It is a cylindrical lens.
第3の実施の形態(図3)のアナモフィック光学系APは、長軸方向の縮小側から順に、第1〜第3回転対称レンズt1〜t3と、長軸方向絞りSXと、第4,第5回転対称レンズt4,t5と、第1〜第3アナモフィックレンズa1〜a3と、短軸方向絞りSYと、第4,第5アナモフィックレンズa4,a5と、から成っている。第1回転対称レンズt1は正パワーを有するメニスカスレンズであり、第2回転対称レンズt2は正パワーを有する両凸レンズであり、第3回転対称レンズt3は正パワーを有する平凸レンズであり、第4,第5回転対称レンズt4,t5は負パワーを有する両凹レンズである。第1,第2アナモフィックレンズa1,a2は長軸方向に正パワーを有するシリンドリカルレンズであり、第3,第4アナモフィックレンズa3,a4は短軸方向に正パワーを有するシリンドリカルレンズであり、第5アナモフィックレンズa5は長軸方向に正パワーを有するシリンドリカルレンズである。 The anamorphic optical system AP of the third embodiment (FIG. 3) includes, in order from the reduction side in the long axis direction, first to third rotationally symmetric lenses t1 to t3, a long axis direction stop SX, and fourth and fourth. It consists of five rotationally symmetric lenses t4 and t5, first to third anamorphic lenses a1 to a3, a short-axis direction stop SY, and fourth and fifth anamorphic lenses a4 and a5. The first rotationally symmetric lens t1 is a meniscus lens having positive power, the second rotationally symmetric lens t2 is a biconvex lens having positive power, the third rotationally symmetric lens t3 is a planoconvex lens having positive power, and the fourth The fifth rotationally symmetric lenses t4 and t5 are biconcave lenses having negative power. The first and second anamorphic lenses a1 and a2 are cylindrical lenses having positive power in the major axis direction, and the third and fourth anamorphic lenses a3 and a4 are cylindrical lenses having positive power in the minor axis direction. The anamorphic lens a5 is a cylindrical lens having positive power in the long axis direction.
第4の実施の形態(図4)のアナモフィック光学系APは、長軸方向の縮小側から順に、第1〜第3回転対称レンズt1〜t3と、長軸方向絞りSXと、第4,第5回転対称レンズt4,t5と、第1〜第3アナモフィックレンズa1〜a3と、短軸方向絞りSYと、第4,第5アナモフィックレンズa4,a5と、から成っている。第1回転対称レンズt1は正パワーを有するメニスカスレンズであり、第2回転対称レンズt2は正パワーを有する両凸レンズであり、第3回転対称レンズt3は正パワーを有する平凸レンズであり、第4,第5回転対称レンズt4,t5は負パワーを有する両凹レンズである。第1,第2アナモフィックレンズa1,a2は長軸方向に正パワーを有するシリンドリカルレンズであり、第3,第4アナモフィックレンズa3,a4は短軸方向に正パワーを有するシリンドリカルレンズであり、第5アナモフィックレンズa5は長軸方向に正パワーを有するシリンドリカルレンズである。 The anamorphic optical system AP of the fourth embodiment (FIG. 4) includes, in order from the reduction side in the long axis direction, first to third rotationally symmetric lenses t1 to t3, a long axis direction stop SX, and fourth and fourth. It consists of five rotationally symmetric lenses t4 and t5, first to third anamorphic lenses a1 to a3, a short-axis direction stop SY, and fourth and fifth anamorphic lenses a4 and a5. The first rotationally symmetric lens t1 is a meniscus lens having positive power, the second rotationally symmetric lens t2 is a biconvex lens having positive power, the third rotationally symmetric lens t3 is a planoconvex lens having positive power, and the fourth The fifth rotationally symmetric lenses t4 and t5 are biconcave lenses having negative power. The first and second anamorphic lenses a1 and a2 are cylindrical lenses having positive power in the major axis direction, and the third and fourth anamorphic lenses a3 and a4 are cylindrical lenses having positive power in the minor axis direction. The anamorphic lens a5 is a cylindrical lens having positive power in the long axis direction.
全体としてアナモ比(=|長軸方向の倍率/短軸方向の倍率|)が大きく、かつ、レンズ枚数が少ないアナモフィック光学系を構成するには、光軸に対して回転対称な回転対称レンズと、互いに垂直な方向の曲率が異なる面を含むアナモフィックレンズと、をそれぞれ1枚以上有する構成にするのが好ましい。その場合、例えば第1の実施の形態のように、1枚以上の回転対称レンズから成る回転対称レンズ群t1〜t4と、1枚以上のアナモフィックレンズから成るアナモフィックレンズ群a1〜a10と、が独立して存在する配置にしてもよく、第2の実施の形態のように、1枚以上の回転対称レンズから成る回転対称レンズ群t1〜t7と、1枚以上のアナモフィックレンズから成るアナモフィックレンズ群a1〜a8と、が混在した配置にしてもよい。 To construct an anamorphic optical system having a large anamorphic ratio (= | magnification in the major axis direction / magnification in the minor axis direction |) as a whole and a small number of lenses, a rotationally symmetric lens that is rotationally symmetric with respect to the optical axis is used. It is preferable to have a configuration in which at least one anamorphic lens including surfaces having different curvatures in directions perpendicular to each other is included. In that case, for example, as in the first embodiment, rotationally symmetric lens groups t1 to t4 composed of one or more rotationally symmetric lenses and anamorphic lens groups a1 to a10 composed of one or more anamorphic lenses are independent. As in the second embodiment, the rotationally symmetric lens groups t1 to t7 composed of one or more rotationally symmetric lenses and the anamorphic lens group a1 composed of one or more anamorphic lenses, as in the second embodiment. -A8 may be mixed.
アナモフィック光学系を構成する場合、すべてのレンズを長軸方向か短軸方向のどちらかにパワーを持つシリンドリカルレンズのみで構成すると、倍率の異なる2本の光学系を持つことと等価になるため、レンズ枚数が倍増してしまう。また、長軸方向と短軸方向の両方にパワーを持つトロイダルレンズを使用すると、レンズ枚数は少なくできるが、個々のトロイダルレンズは製作が難しく高価であるため、結局は高価な光学系になってしまう。さらに、倍率の異なるアナモフィック光学系の各レンズ間隔を等しくしなければならず、像面の補正や歪曲の補正に対し不利になる。 When configuring an anamorphic optical system, if all lenses are composed of only cylindrical lenses having power in either the major axis direction or the minor axis direction, it is equivalent to having two optical systems with different magnifications. The number of lenses will double. In addition, if a toroidal lens having power in both the long axis direction and the short axis direction is used, the number of lenses can be reduced. However, since individual toroidal lenses are difficult to manufacture and are expensive, it eventually becomes an expensive optical system. End up. Furthermore, it is necessary to make the lens intervals of the anamorphic optical systems having different magnifications equal, which is disadvantageous for image plane correction and distortion correction.
したがって、アナモフィック光学系のレンズ枚数を少なくしてもコストアップを招かないようにするには、回転対称レンズとアナモフィックレンズとを共に有する構成にすることが好ましい。例えば各実施の形態のように、光軸AXに対して回転対称な回転対称レンズtiと、互いに垂直な方向の曲率が異なる面を含むアナモフィックレンズajと、をそれぞれ1枚以上有する構成が好ましい。こうすることにより、アナモフィックレンズのみで構成するよりも、レンズ枚数の削減を効果的に行うことができる。また、短軸方向と長軸方向の倍率に起因する収差の発生に対しても、アナモフィックレンズ部分の構成の自由度があるため、収差補正が容易になる。なお、上記アナモフィックレンズはシリンドリカルレンズに限定されない。アナモフィックレンズとしてトロイダルレンズを含む構成でもよく、その場合でも同様の効果を得ることができる。 Therefore, in order not to increase the cost even if the number of lenses of the anamorphic optical system is reduced, it is preferable to have a configuration having both a rotationally symmetric lens and an anamorphic lens. For example, as in each embodiment, it is preferable to have at least one rotationally symmetric lens ti that is rotationally symmetric with respect to the optical axis AX and one or more anamorphic lenses aj that include surfaces having different curvatures in directions perpendicular to each other. In this way, the number of lenses can be reduced more effectively than when only an anamorphic lens is used. In addition, the aberration correction can be easily performed because there is a degree of freedom in the configuration of the anamorphic lens portion even with respect to the occurrence of aberration due to the magnification in the minor axis direction and the major axis direction. The anamorphic lens is not limited to a cylindrical lens. A configuration including a toroidal lens as the anamorphic lens may be used, and even in this case, the same effect can be obtained.
回転対称レンズとアナモフィックレンズとを共に有するアナモフィック光学系においては、回転対称レンズ群(すなわち全回転対称レンズのみから成るレンズ群)とアナモフィックレンズ群(すなわち全アナモフィックレンズのみから成るレンズ群)とに対して適切にパワーを振り分けることが重要になる。全系に占める回転対称レンズ群のパワーと、全系に占めるアナモフィックレンズ群のパワーと、を適切に配分することにより、更にコンパクトかつ効率的でレンズ枚数の少ないアナモフィック光学系を実現することができる。また、両者に共通のパワーを回転対称レンズ群に負担させることにより、長軸方向だけ又は短軸方向だけで各方向のパワーを負担するよりも、効率的なパワー配置が可能となる。 In an anamorphic optical system having both a rotationally symmetric lens and an anamorphic lens, a rotationally symmetric lens group (that is, a lens group that includes only all rotationally symmetric lenses) and an anamorphic lens group (that is, a lens group that includes only all anamorphic lenses). It is important to distribute power appropriately. By appropriately allocating the power of the rotationally symmetric lens group occupying the entire system and the power of the anamorphic lens group occupying the entire system, it is possible to realize a more compact and efficient anamorphic optical system with a small number of lenses. . In addition, by causing the rotationally symmetric lens group to share power common to both, it is possible to arrange power more efficiently than to bear power in each direction only in the long axis direction or only in the short axis direction.
また、収差補正の観点から考えると、長軸方向と短軸方向とに共通の収差補正を回転対称レンズ群で行い、その残りの収差と倍率の差に起因する収差とについては、アナモフィックレンズ群で補正を行う方がより効率的であり好ましい。両者に共通する収差の大部分を回転対称レンズ群で行えば、アナモフィックレンズ群で長軸方向,短軸方向共に収差補正を行う必要がなくなる。したがってレンズ枚数の削減が可能となり、さらにアナモフィック光学系の高性能化が可能となる。 From the viewpoint of aberration correction, the aberration correction common to the major axis direction and the minor axis direction is performed by the rotationally symmetric lens group, and the remaining aberration and the aberration caused by the difference in magnification are analyzed by the anamorphic lens group. It is more efficient and preferable to perform the correction. If most of the aberrations common to both are performed by the rotationally symmetric lens group, it is not necessary to correct aberrations in the major axis direction and the minor axis direction by the anamorphic lens group. Therefore, the number of lenses can be reduced, and further the performance of the anamorphic optical system can be improved.
前記パワー配分に関しては、以下の条件式(1)を満足することが望ましい。 Regarding the power distribution, it is desirable that the following conditional expression (1) is satisfied.
1.90<|fXall/fsym|<20.00 …(1)
ただし、
fXall:アナモフィック光学系の長軸方向の焦点距離、
fsym:全回転対称レンズのみから成るレンズ群の焦点距離、
である。
1.90 <| fXall / fsym | <20.00… (1)
However,
fXall: Focal length in the long axis direction of the anamorphic optical system,
fsym: focal length of a lens group consisting only of all rotationally symmetric lenses,
It is.
条件式(1)は、回転対称レンズ群のパワー(=1/fsym)が長軸方向における全系のパワー(=1/fXall)に占める割合の好ましい範囲を規定している。条件式(1)の下限を越えて回転対称レンズ群のパワーが弱くなると、アナモフィック光学系全体に占める回転対称レンズの枚数は少なくて済むが、長軸方向・短軸方向に共通のパワー配分が減るため、アナモフィックレンズの枚数が増加し、アナモフィック光学系が高価になってしまう。また、両方向に共通な収差補正が不十分になるため、やはりアナモフィックレンズの枚数が増加し、アナモフィック光学系が高価になってしまうか、あるいはコンパクト化が困難になる。逆に、条件式(1)の上限を越えて回転対称レンズ群のパワーが強くなると、両方向に共通な収差補正が過剰になるか、あるいは新たな収差が発生し、その補正のためにアナモフィックレンズの枚数が増加し、アナモフィック光学系が高価になってしまうか、あるいは高性能化が困難になる。 Conditional expression (1) defines a preferable range of the ratio of the power (= 1 / fsym) of the rotationally symmetric lens group to the total system power (= 1 / fXall) in the major axis direction. If the power of the rotationally symmetric lens group becomes weaker than the lower limit of conditional expression (1), the number of rotationally symmetric lenses in the entire anamorphic optical system can be reduced, but there is a common power distribution in the major axis direction and minor axis direction. Therefore, the number of anamorphic lenses increases, and the anamorphic optical system becomes expensive. In addition, since aberration correction common to both directions becomes insufficient, the number of anamorphic lenses also increases, and the anamorphic optical system becomes expensive or difficult to downsize. Conversely, if the power of the rotationally symmetric lens group increases beyond the upper limit of conditional expression (1), aberration correction common to both directions becomes excessive, or new aberration occurs, and anamorphic lenses are used for the correction. This increases the number of the anamorphic optical systems, or makes it difficult to achieve high performance.
以下の条件式(1a)を満足することが更に望ましい。条件式(1a)は、上記条件式(1)が規定している条件範囲のなかでも、上記観点等に基づいてより一層好ましい条件範囲を規定している。 It is more desirable to satisfy the following conditional expression (1a). Conditional expression (1a) defines a more preferable condition range based on the above viewpoints, etc., among the condition ranges defined by conditional expression (1).
2.00<|fXall/fsym|<10.00 …(1a) 2.00 <| fXall / fsym | <10.00… (1a)
前記アナモ比に関しては、以下の条件式(2)を満足することが望ましい。また、レンズ枚数の削減及び光学性能の向上とのバランスをとりながら大きなアナモ比を得るためには、前記条件式(1)とともに条件式(2)を満足することが更に望ましい。 Regarding the anamorphic ratio, it is desirable to satisfy the following conditional expression (2). In order to obtain a large anamorphic ratio while balancing the reduction in the number of lenses and the improvement in optical performance, it is more desirable to satisfy conditional expression (2) together with conditional expression (1).
6.4<|βlong/βshort|<30.0 …(2)
ただし、
βlong:アナモフィック光学系の長軸方向の倍率、
βshort:アナモフィック光学系の短軸方向の倍率、
である。
6.4 <| βlong / βshort | <30.0 (2)
However,
βlong: magnification in the long axis direction of the anamorphic optical system,
βshort: magnification in the minor axis direction of the anamorphic optical system,
It is.
条件式(2)は、レンズ枚数の削減,光学性能の向上及びアナモ比の増大を両立させる上で好ましいアナモ比の範囲を規定している。条件式(2)の下限を越えてアナモ比が小さくなると、アナモフィック光学系のメリットが少なくなる。例えば、縦横比の非常に大きな物体面や光学素子面(例えば表示素子面)の照明に対応することができなくなる。また、縦横の大きさの比が大きく歪んだ像を元の歪みのない像として観察する場合、逆に像の縦横の大きさの比を大きく歪ませて観察する場合に対応することができなくなる。条件式(2)の上限を越えてアナモ比が大きくなると、収差補正が困難になり、その補正のためにアナモフィック光学系が大型化してしまう。また、レンズ枚数も飛躍的に増えてしまうため、アナモフィック光学系は高価になってしまう。 Conditional expression (2) defines a preferable range of the anamorphic ratio in order to achieve both a reduction in the number of lenses, an improvement in optical performance, and an increase in the anamorphic ratio. When the anamorphic ratio is reduced beyond the lower limit of conditional expression (2), the merit of the anamorphic optical system is reduced. For example, it becomes impossible to deal with illumination of an object surface or an optical element surface (for example, a display element surface) having a very large aspect ratio. In addition, when observing an image with a large ratio of vertical and horizontal size as a distortion-free image, it is not possible to cope with a case where the image is observed with a large distortion of the vertical and horizontal size. . If the anamorphic ratio increases beyond the upper limit of conditional expression (2), it becomes difficult to correct aberrations, and the anamorphic optical system becomes large due to the correction. In addition, the number of lenses increases dramatically, and the anamorphic optical system becomes expensive.
以下の条件式(2a)を満足することが更に望ましい。条件式(2a)は、上記条件式(2)が規定している条件範囲のなかでも、上記観点等に基づいてより一層好ましい条件範囲を規定している。 It is more desirable to satisfy the following conditional expression (2a). Conditional expression (2a) defines a more preferable condition range based on the above viewpoints, etc., among the condition ranges defined by conditional expression (2).
10.0<|βlong/βshort|<20.0 …(2a) 10.0 <| βlong / βshort | <20.0… (2a)
図9に、アナモフィック光学系APとして第1の実施の形態(図1)を備えた照明光学系の概略光学構成を短軸方向について示す。この照明光学系は、光源1からの光を被照射面IMに導く照明光学系であって、光源1が第1焦点F1近傍に位置するように配置された楕円面鏡2と、その楕円面鏡2の第2焦点F2近傍に入射端面3aを持つオプティカルインテグレータ3と、そのオプティカルインテグレータ3の射出端面3bの像を被照射面IM上に形成するアナモフィック光学系APと、を有しており、光源1を含めた状態で照明装置の主要部を構成している。
FIG. 9 shows a schematic optical configuration of the illumination optical system provided with the first embodiment (FIG. 1) as the anamorphic optical system AP in the minor axis direction. This illumination optical system is an illumination optical system that guides light from the light source 1 to the irradiated surface IM, and an
集光光学系として機能する楕円面鏡2は、2つの焦点F1,F2を持つ回転楕円形状の反射面を有しており、楕円面鏡2に近い側の第1焦点F1に位置する光源1からの光を集光して、第2焦点F2位置に2次光源を形成する。光源1としては、例えば、ハロゲンランプ,水銀ランプ,レーザー光源等、様々なタイプのものが利用可能であり、特定の光源に限定されない。なお、楕円面鏡2の代わりに回転放物面鏡や球面鏡等を用いてもよいが、その場合、光源からの光を集光するために、集光レンズ等と組み合わせて集光光学系を構成する必要がある。
The
楕円面鏡2の第2焦点F2近傍にはオプティカルインテグレータ3の入射端面3aが位置しているので、楕円面鏡2から射出した光はオプティカルインテグレータ3の入射端面3a近傍で結像することになる。図9に示すオプティカルインテグレータ3は、4枚の平面ミラーを貼り合わせて成る中空ロッド方式のオプティカルインテグレータ(いわゆるオプティカルインテグレータロッド)であり、入射端面3aから入射してきた光を側面(すなわち内壁面)で何度も繰り返し反射させることによりミキシングし、光の空間的なエネルギー分布を均一化して射出端面3bから射出する。その射出端面3bと被照射面IMとはアナモフィック光学系APに関して共役な関係になっているため、射出端面3b位置の均一な光強度分布状態はアナモフィック光学系APにより被照射面IMに転写される。したがって、上記ミキシング効果により射出端面3bでの光強度分布が均一化された光束は、被照射面IMを効率良く均一に照明することになる。なお、被照射面IMとしては、物体面,光学素子面(例えば表示素子面)等が挙げられるが、それらに限定するものではなく、照明が必要とされるものすべてが対象となる。
Since the
一般的なオプティカルインテグレータの形状は、加工のし易さ,均一性の確保等の観点から直方体になっている。そのため、オプティカルインテグレータの入射端面形状や射出端面形状は共に長方形であることが多い。しかし、図9に示す照明光学系の場合、第2焦点F2近傍での光束断面形状が円形に近くなることを考慮して、光利用効率を良くするために、オプティカルインテグレータ3の入射端面3aを光束断面よりも大きい正方形としている。射出端面3bの形状も、加工のし易さ,均一性の確保等の観点から入射端面3aと同様に正方形としているが、これに限定するものではない。この照明光学系では、照明を必要とする被照射面IMの形状に射出端面3bの形状を適合させる必要がないからである。一般に、照明を必要とする被照射面の形状は様々であり、例えば、表示素子面の形状は正方形の場合もあれば長方形の場合もある。また、表示素子面を構成する画素の集まりを照明する場合も同様であり、その照明を必要とする領域が正方形の場合もあれば長方形の場合もある。いずれにしても照明を必要とする領域の縦横比は多様であり、その領域の形状がオプティカルインテグレータの射出端面の形状と相似でなければ、通常の回転対称光学系を使用した照明では光利用効率が非常に低くなってしまう。
The shape of a general optical integrator is a rectangular parallelepiped from the viewpoint of ease of processing and ensuring uniformity. Therefore, both the incident end face shape and the exit end face shape of the optical integrator are often rectangular. However, in the case of the illumination optical system shown in FIG. 9, in consideration of the fact that the cross-sectional shape of the light beam in the vicinity of the second focal point F2 is almost circular, the
図9に示す照明光学系では、照明を必要とする領域の形状とオプティカルインテグレータの射出端面の形状との不適合を、アナモフィック光学系APを用いることにより解消している。つまり、正方形の射出端面3bから射出した光束を、アナモフィック光学系APで被照射面IMの照明を必要とする領域の形状に近づけることにより、光利用効率を高めているのである。オプティカルインテグレータ3の射出端面3bが被照射面IM上で結像する構成に変わりはないので、光強度分布の均一性も保たれる。このようにアナモフィック光学系を用いて照明光学系や照明装置を構成すれば、これらの軽量・コンパクト化,低コスト化,高性能化,光利用効率の向上等に寄与することができる。特に、照明を必要とする領域の形状が縦横比の大きい長方形である場合には有効である。
In the illumination optical system shown in FIG. 9, the incompatibility between the shape of the area requiring illumination and the shape of the exit end face of the optical integrator is eliminated by using the anamorphic optical system AP. That is, the light utilization efficiency is improved by bringing the light beam emitted from the square
以下、本発明を実施したアナモフィック光学系を、コンストラクションデータ等を挙げて更に具体的に説明する。ここで挙げる実施例1〜4は、前述した第1〜第4の実施の形態にそれぞれ対応する数値実施例であり、第1〜第4の実施の形態を表すレンズ構成図(図1〜図4)は、対応する実施例1〜4のレンズ構成をそれぞれ示している。 Hereinafter, the anamorphic optical system embodying the present invention will be described more specifically with reference to construction data and the like. Examples 1 to 4 listed here are numerical examples corresponding to the first to fourth embodiments, respectively, and are lens configuration diagrams showing the first to fourth embodiments (FIGS. 1 to 4). 4) shows the lens configurations of the corresponding Examples 1 to 4, respectively.
各実施例のコンストラクションデータでは、各レンズ構成図の(A)に対応する長軸方向のレンズ構成データと、各レンズ構成図の(B)に対応する短軸方向のレンズ構成データと、を挙げている。各コンストラクションデータにおいて、ri(i=1,2,3,...)は物体側から数えてi番目の面の曲率半径(mm)、di(i=1,2,3,...)は物体側から数えてi番目の軸上面間隔(mm)を示しており、Ni(i=1,2,3,...),νi(i=1,2,3,...)は物体側から数えてi番目のレンズのd線に対する屈折率(Nd),アッベ数(νd)を示している。また、全系の倍率β,開口数NA,物体距離S1{すなわち第1面(r1)から物体までの距離(mm)}及び設計波長λ(nm)を他のデータとあわせて示し、表1に各条件式規定のパラメータに対応するデータを各実施例について示す。 In the construction data of each example, the lens configuration data in the major axis direction corresponding to (A) in each lens configuration diagram and the lens configuration data in the minor axis direction corresponding to (B) in each lens configuration diagram are given. ing. In each construction data, ri (i = 1,2,3, ...) is the radius of curvature (mm) of the i-th surface counting from the object side, di (i = 1,2,3, ...) Indicates the i-th axis top surface distance (mm) counted from the object side, and Ni (i = 1,2,3, ...), νi (i = 1,2,3, ...) is The refractive index (Nd) and Abbe number (νd) for the d-line of the i-th lens counted from the object side are shown. Table 1 shows the magnification β, numerical aperture NA, object distance S1 {that is, the distance from the first surface (r1) to the object (mm)}, and the design wavelength λ (nm) together with other data. The data corresponding to the parameters defined in each conditional expression are shown for each example.
図5〜図8は、実施例1〜実施例4に対応する収差図である。図5〜図8中、(A)〜(C)は長軸方向の収差図、(D)〜(F)は短軸方向の収差図であり、(A)と(D)は球面収差図、(B)と(E)は非点収差図、(C)と(F)は歪曲収差図である{NA:開口数,Y':最大像高(mm)}。球面収差図において、実線は設計波長λに対する球面収差量(mm)を表しており、破線SCは正弦条件不満足量(mm)を表している。非点収差図において、破線DMはメリディオナル面、実線DSはサジタル面でのd線に対する各非点収差(mm)を表している。また、歪曲収差図において実線はd線に対する歪曲(%)を表している。 5 to 8 are aberration diagrams corresponding to Examples 1 to 4. FIG. 5 to 8, (A) to (C) are aberration diagrams in the major axis direction, (D) to (F) are aberration diagrams in the minor axis direction, and (A) and (D) are spherical aberration diagrams. , (B) and (E) are astigmatism diagrams, and (C) and (F) are distortion diagrams {NA: numerical aperture, Y ′: maximum image height (mm)}. In the spherical aberration diagram, the solid line represents the spherical aberration amount (mm) with respect to the design wavelength λ, and the broken line SC represents the sine condition unsatisfactory amount (mm). In the astigmatism diagram, the broken line DM represents the meridional surface, and the solid line DS represents each astigmatism (mm) with respect to the d-line on the sagittal surface. In the distortion diagram, the solid line represents the distortion (%) with respect to the d-line.
《実施例1の長軸方向データ》
β=-6.6,NA=0.085,S1=-1.5,λ=435.84
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= ∞
d1= 9.900 N1= 1.52667 ν1= 64.20(t1)
r2= -18.088
d2= 0.300
r3= ∞
d3= 3.000 N2= 1.52667 ν2= 64.20(t2)
r4= 62.016
d4= 2.633
r5= ∞
d5= 11.400 N3= 1.52667 ν3= 64.20(t3)
r6= -25.840
d6= 0.300
r7= ∞
d7= 13.000 N4= 1.52667 ν4= 64.20(t4)
r8= -36.176
d8= 11.183
r9= ∞
d9= 3.000 N5= 1.52667 ν5= 64.20(a1)
r10= 51.680
d10= 2.865
r11= ∞
d11= 6.000 N6= 1.52667 ν6= 64.20(a2)
r12= -77.520
d12= 7.178
r13= ∞(SX)
d13= 0.500
r14= ∞
d14= 5.000 N7= 1.52667 ν7= 64.20(a3)
r15=-103.360
d15=29.363
r16= ∞
d16= 6.000 N8= 1.52667 ν8= 64.20(a4)
r17= -77.520
d17=78.749
r18= ∞
d18= 6.000 N9= 1.52667 ν9= 64.20(a5)
r19= ∞
d19= 0.300
r20= ∞(SY)
d20= 0.300
r21= ∞
d21= 6.000 N10=1.52667 ν10=64.20(a6)
r22= ∞
d22=12.172
r23= ∞
d23= 3.000 N11=1.52667 ν11=64.20(a7)
r24= ∞
d24=49.527
r25= ∞
d25= 4.000 N12=1.52667 ν12=64.20(a8)
r26= ∞
d26=14.525
r27= ∞
d27= 8.000 N13=1.52667 ν13=64.20(a9)
r28= ∞
d28= 0.300
r29= ∞
d29= 8.000 N14=1.52667 ν14=64.20(a10)
r30= ∞
<< Long axis direction data of Example 1 >>
β = -6.6, NA = 0.085, S1 = -1.5, λ = 435.84
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = ∞
d1 = 9.900 N1 = 1.52667 ν1 = 64.20 (t1)
r2 = -18.088
d2 = 0.300
r3 = ∞
d3 = 3.000 N2 = 1.52667 ν2 = 64.20 (t2)
r4 = 62.016
d4 = 2.633
r5 = ∞
d5 = 11.400 N3 = 1.52667 ν3 = 64.20 (t3)
r6 = -25.840
d6 = 0.300
r7 = ∞
d7 = 13.000 N4 = 1.52667 ν4 = 64.20 (t4)
r8 = -36.176
d8 = 11.183
r9 = ∞
d9 = 3.000 N5 = 1.52667 ν5 = 64.20 (a1)
r10 = 51.680
d10 = 2.865
r11 = ∞
d11 = 6.000 N6 = 1.52667 ν6 = 64.20 (a2)
r12 = -77.520
d12 = 7.178
r13 = ∞ (SX)
d13 = 0.500
r14 = ∞
d14 = 5.000 N7 = 1.52667 ν7 = 64.20 (a3)
r15 = -103.360
d15 = 29.363
r16 = ∞
d16 = 6.000 N8 = 1.52667 ν8 = 64.20 (a4)
r17 = -77.520
d17 = 78.749
r18 = ∞
d18 = 6.000 N9 = 1.52667 ν9 = 64.20 (a5)
r19 = ∞
d19 = 0.300
r20 = ∞ (SY)
d20 = 0.300
r21 = ∞
d21 = 6.000 N10 = 1.52667 ν10 = 64.20 (a6)
r22 = ∞
d22 = 12.172
r23 = ∞
d23 = 3.000 N11 = 1.52667 ν11 = 64.20 (a7)
r24 = ∞
d24 = 49.527
r25 = ∞
d25 = 4.000 N12 = 1.52667 ν12 = 64.20 (a8)
r26 = ∞
d26 = 14.525
r27 = ∞
d27 = 8.000 N13 = 1.52667 ν13 = 64.20 (a9)
r28 = ∞
d28 = 0.300
r29 = ∞
d29 = 8.000 N14 = 1.52667 ν14 = 64.20 (a10)
r30 = ∞
《実施例1の短軸方向データ》
β=-1.3,NA=0.43,S1=-1.5,λ=435.84
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= ∞
d1= 9.900 N1= 1.52667 ν1= 64.20(t1)
r2= -18.088
d2= 0.300
r3= ∞
d3= 3.000 N2= 1.52667 ν2= 64.20(t2)
r4= 62.016
d4= 2.633
r5= ∞
d5= 11.400 N3= 1.52667 ν3= 64.20(t3)
r6= -25.840
d6= 0.300
r7= ∞
d7= 13.000 N4= 1.52667 ν4= 64.20(t4)
r8= -36.176
d8= 11.183
r9= ∞
d9= 3.000 N5= 1.52667 ν5= 64.20(a1)
r10= ∞
d10= 2.865
r11= ∞
d11= 6.000 N6= 1.52667 ν6= 64.20(a2)
r12= ∞
d12= 7.178
r13= ∞(SX)
d13= 0.500
r14= ∞
d14= 5.000 N7= 1.52667 ν7= 64.20(a3)
r15= ∞
d15=29.363
r16= ∞
d16= 6.000 N8= 1.52667 ν8= 64.20(a4)
r17= ∞
d17=78.749
r18= ∞
d18= 6.000 N9= 1.52667 ν9= 64.20(a5)
r19= -77.520
d19= 0.300
r20= ∞(SY)
d20= 0.300
r21= 77.520
d21= 6.000 N10=1.52667 ν10=64.20(a6)
r22= ∞
d22=12.172
r23= -51.680
d23= 3.000 N11=1.52667 ν11=64.20(a7)
r24= ∞
d24=49.527
r25= 155.040
d25= 4.000 N12=1.52667 ν12=64.20(a8)
r26= ∞
d26=14.525
r27= 51.680
d27= 8.000 N13=1.52667 ν13=64.20(a9)
r28= ∞
d28= 0.300
r29= 51.680
d29= 8.000 N14=1.52667 ν14=64.20(a10)
r30= ∞
<< Short Axis Data of Example 1 >>
β = -1.3, NA = 0.43, S1 = -1.5, λ = 435.84
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = ∞
d1 = 9.900 N1 = 1.52667 ν1 = 64.20 (t1)
r2 = -18.088
d2 = 0.300
r3 = ∞
d3 = 3.000 N2 = 1.52667 ν2 = 64.20 (t2)
r4 = 62.016
d4 = 2.633
r5 = ∞
d5 = 11.400 N3 = 1.52667 ν3 = 64.20 (t3)
r6 = -25.840
d6 = 0.300
r7 = ∞
d7 = 13.000 N4 = 1.52667 ν4 = 64.20 (t4)
r8 = -36.176
d8 = 11.183
r9 = ∞
d9 = 3.000 N5 = 1.52667 ν5 = 64.20 (a1)
r10 = ∞
d10 = 2.865
r11 = ∞
d11 = 6.000 N6 = 1.52667 ν6 = 64.20 (a2)
r12 = ∞
d12 = 7.178
r13 = ∞ (SX)
d13 = 0.500
r14 = ∞
d14 = 5.000 N7 = 1.52667 ν7 = 64.20 (a3)
r15 = ∞
d15 = 29.363
r16 = ∞
d16 = 6.000 N8 = 1.52667 ν8 = 64.20 (a4)
r17 = ∞
d17 = 78.749
r18 = ∞
d18 = 6.000 N9 = 1.52667 ν9 = 64.20 (a5)
r19 = -77.520
d19 = 0.300
r20 = ∞ (SY)
d20 = 0.300
r21 = 77.520
d21 = 6.000 N10 = 1.52667 ν10 = 64.20 (a6)
r22 = ∞
d22 = 12.172
r23 = -51.680
d23 = 3.000 N11 = 1.52667 ν11 = 64.20 (a7)
r24 = ∞
d24 = 49.527
r25 = 155.040
d25 = 4.000 N12 = 1.52667 ν12 = 64.20 (a8)
r26 = ∞
d26 = 14.525
r27 = 51.680
d27 = 8.000 N13 = 1.52667 ν13 = 64.20 (a9)
r28 = ∞
d28 = 0.300
r29 = 51.680
d29 = 8.000 N14 = 1.52667 ν14 = 64.20 (a10)
r30 = ∞
《実施例2の長軸方向データ》
β=-6.6,NA=0.03,S1=-1.5,λ=435.84
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -15.631
d1= 2.430 N1= 1.79149 ν1= 27.51(t1)
r2= -452.227
d2= 4.010
r3= -42.111
d3= 2.000 N2= 1.70011 ν2= 32.10(t2)
r4= 19.316
d4= 0.861
r5= ∞
d5= 6.700 N3= 1.52667 ν3= 64.20(t3)
r6= -12.980
d6= 0.647
r7= ∞
d7= 5.600 N4= 1.52667 ν4= 64.20(t4)
r8= -15.570
d8= 3.703
r9= ∞
d9= 3.400 N5= 1.52667 ν5= 64.20(t5)
r10= -36.330
d10= 0.300
r11= ∞
d11= 3.200 N6= 1.52667 ν6= 64.20(t6)
r12= -41.520
d12= 0.300
r13= ∞(ST)
d13= 0.500
r14= ∞
d14= 2.300 N7= 1.52667 ν7= 64.20(a1)
r15= ∞
d15=17.668
r16= 452.227
d16= 2.430 N8= 1.79149 ν8= 27.51(t7)
r17= 15.631
d17= 2.920
r18= ∞
d18= 6.000 N9= 1.52667 ν9= 64.20(a2)
r19= -77.520
d19= 1.036
r20= 51.680
d20= 8.000 N10=1.52667 ν10=64.20(a3)
r21= ∞
d21= 5.632
r22= ∞
d22= 7.000 N11=1.52667 ν11=64.20(a4)
r23= ∞
d23= 0.300
r24= ∞
d24= 8.000 N12=1.52667 ν12=64.20(a5)
r25= ∞
d25=37.369
r26= ∞
d26= 8.000 N13=1.52667 ν13=64.20(a6)
r27= ∞
d27= 2.680
r28= 51.680
d28= 8.000 N14=1.52667 ν14=64.20(a7)
r29= ∞
d29=17.837
r30= ∞
d30= 8.000 N15=1.52667 ν15=64.20(a8)
r31= ∞
<< Long-axis direction data of Example 2 >>
β = -6.6, NA = 0.03, S1 = -1.5, λ = 435.84
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -15.631
d1 = 2.430 N1 = 1.79149 ν1 = 27.51 (t1)
r2 = -452.227
d2 = 4.010
r3 = -42.111
d3 = 2.000 N2 = 1.70011 ν2 = 32.10 (t2)
r4 = 19.316
d4 = 0.861
r5 = ∞
d5 = 6.700 N3 = 1.52667 ν3 = 64.20 (t3)
r6 = -12.980
d6 = 0.647
r7 = ∞
d7 = 5.600 N4 = 1.52667 ν4 = 64.20 (t4)
r8 = -15.570
d8 = 3.703
r9 = ∞
d9 = 3.400 N5 = 1.52667 ν5 = 64.20 (t5)
r10 = -36.330
d10 = 0.300
r11 = ∞
d11 = 3.200 N6 = 1.52667 ν6 = 64.20 (t6)
r12 = -41.520
d12 = 0.300
r13 = ∞ (ST)
d13 = 0.500
r14 = ∞
d14 = 2.300 N7 = 1.52667 ν7 = 64.20 (a1)
r15 = ∞
d15 = 17.668
r16 = 452.227
d16 = 2.430 N8 = 1.79149 ν8 = 27.51 (t7)
r17 = 15.631
d17 = 2.920
r18 = ∞
d18 = 6.000 N9 = 1.52667 ν9 = 64.20 (a2)
r19 = -77.520
d19 = 1.036
r20 = 51.680
d20 = 8.000 N10 = 1.52667 ν10 = 64.20 (a3)
r21 = ∞
d21 = 5.632
r22 = ∞
d22 = 7.000 N11 = 1.52667 ν11 = 64.20 (a4)
r23 = ∞
d23 = 0.300
r24 = ∞
d24 = 8.000 N12 = 1.52667 ν12 = 64.20 (a5)
r25 = ∞
d25 = 37.369
r26 = ∞
d26 = 8.000 N13 = 1.52667 ν13 = 64.20 (a6)
r27 = ∞
d27 = 2.680
r28 = 51.680
d28 = 8.000 N14 = 1.52667 ν14 = 64.20 (a7)
r29 = ∞
d29 = 17.837
r30 = ∞
d30 = 8.000 N15 = 1.52667 ν15 = 64.20 (a8)
r31 = ∞
《実施例2の短軸方向データ》
β=-1.0,NA=0.021,S1=-1.5,λ=435.84
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -15.631
d1= 2.430 N1= 1.79149 ν1= 27.51(t1)
r2= -452.227
d2= 4.010
r3= -42.111
d3= 2.000 N2= 1.70011 ν2= 32.10(t2)
r4= 19.316
d4= 0.861
r5= ∞
d5= 6.700 N3= 1.52667 ν3= 64.20(t3)
r6= -12.980
d6= 0.647
r7= ∞
d7= 5.600 N4= 1.52667 ν4= 64.20(t4)
r8= -15.570
d8= 3.703
r9= ∞
d9= 3.400 N5= 1.52667 ν5= 64.20(t5)
r10= -36.330
d10= 0.300
r11= ∞
d11= 3.200 N6= 1.52667 ν6= 64.20(t6)
r12= -41.520
d12= 0.300
r13= ∞(ST)
d13= 0.500
r14= ∞
d14= 2.300 N7= 1.52667 ν7= 64.20(a1)
r15= 12.980
d15=17.668
r16= 452.227
d16= 2.430 N8= 1.79149 ν8= 27.51(t7)
r17= 15.631
d17= 2.920
r18= ∞
d18= 6.000 N9= 1.52667 ν9= 64.20(a2)
r19= ∞
d19= 1.036
r20= ∞
d20= 8.000 N10=1.52667 ν10=64.20(a3)
r21= ∞
d21= 5.632
r22= ∞
d22= 7.000 N11=1.52667 ν11=64.20(a4)
r23= -25.950
d23= 0.300
r24= ∞
d24= 8.000 N12=1.52667 ν12=64.20(a5)
r25= -51.680
d25=37.369
r26= 103.360
d26= 8.000 N13=1.52667 ν13=64.20(a6)
r27= ∞
d27= 2.680
r28= ∞
d28= 8.000 N14=1.52667 ν14=64.20(a7)
r29= ∞
d29=17.837
r30= 51.680
d30= 8.000 N15=1.52667 ν15=64.20(a8)
r31= ∞
<< Short Axis Data of Example 2 >>
β = -1.0, NA = 0.021, S1 = -1.5, λ = 435.84
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -15.631
d1 = 2.430 N1 = 1.79149 ν1 = 27.51 (t1)
r2 = -452.227
d2 = 4.010
r3 = -42.111
d3 = 2.000 N2 = 1.70011 ν2 = 32.10 (t2)
r4 = 19.316
d4 = 0.861
r5 = ∞
d5 = 6.700 N3 = 1.52667 ν3 = 64.20 (t3)
r6 = -12.980
d6 = 0.647
r7 = ∞
d7 = 5.600 N4 = 1.52667 ν4 = 64.20 (t4)
r8 = -15.570
d8 = 3.703
r9 = ∞
d9 = 3.400 N5 = 1.52667 ν5 = 64.20 (t5)
r10 = -36.330
d10 = 0.300
r11 = ∞
d11 = 3.200 N6 = 1.52667 ν6 = 64.20 (t6)
r12 = -41.520
d12 = 0.300
r13 = ∞ (ST)
d13 = 0.500
r14 = ∞
d14 = 2.300 N7 = 1.52667 ν7 = 64.20 (a1)
r15 = 12.980
d15 = 17.668
r16 = 452.227
d16 = 2.430 N8 = 1.79149 ν8 = 27.51 (t7)
r17 = 15.631
d17 = 2.920
r18 = ∞
d18 = 6.000 N9 = 1.52667 ν9 = 64.20 (a2)
r19 = ∞
d19 = 1.036
r20 = ∞
d20 = 8.000 N10 = 1.52667 ν10 = 64.20 (a3)
r21 = ∞
d21 = 5.632
r22 = ∞
d22 = 7.000 N11 = 1.52667 ν11 = 64.20 (a4)
r23 = -25.950
d23 = 0.300
r24 = ∞
d24 = 8.000 N12 = 1.52667 ν12 = 64.20 (a5)
r25 = -51.680
d25 = 37.369
r26 = 103.360
d26 = 8.000 N13 = 1.52667 ν13 = 64.20 (a6)
r27 = ∞
d27 = 2.680
r28 = ∞
d28 = 8.000 N14 = 1.52667 ν14 = 64.20 (a7)
r29 = ∞
d29 = 17.837
r30 = 51.680
d30 = 8.000 N15 = 1.52667 ν15 = 64.20 (a8)
r31 = ∞
《実施例3の長軸方向データ》
β=-7.3,NA=0.025,S1=-28.174,λ=436
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -34.868
d1= 5.800 N1= 1.76502 ν1= 44.78(t1)
r2= -22.674
d2= 0.300
r3= 37.278
d3= 6.470 N2= 1.50036 ν2= 83.58(t2)
r4= -50.107
d4= 3.461
r5= 15.570
d5= 5.600 N3= 1.52665 ν3= 64.20(t3)
r6= ∞
d6= 2.071
r7= ∞(SX)
d7= 0.822
r8= -42.111
d8= 2.000 N4= 1.70006 ν4= 32.10(t4)
r9= 19.316
d9= 13.451
r10= -42.111
d10= 2.000 N5= 1.70006 ν5= 32.10(t5)
r11= 19.316
d11=19.225
r12= ∞
d12= 7.000 N6= 1.52665 ν6= 64.20(a1)
r13= -25.950
d13=65.706
r14= 155.040
d14= 4.000 N7= 1.52665 ν7= 64.20(a2)
r15= ∞
d15=44.038
r16= ∞
d16= 5.000 N8= 1.52665 ν8= 64.20(a3)
r17= ∞
d17=182.653
r18= ∞(SY)
d18= 70.024
r19= ∞
d19= 6.000 N9= 1.52665 ν9= 64.20(a4)
r20= ∞
d20= 5.903
r21= 129.200
d21= 4.500 N10=1.52665 ν10=64.20(a5)
r22= ∞
<< Long-axis data of Example 3 >>
β = -7.3, NA = 0.025, S1 = -28.174, λ = 436
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -34.868
d1 = 5.800 N1 = 1.76502 ν1 = 44.78 (t1)
r2 = -22.674
d2 = 0.300
r3 = 37.278
d3 = 6.470 N2 = 1.50036 ν2 = 83.58 (t2)
r4 = -50.107
d4 = 3.461
r5 = 15.570
d5 = 5.600 N3 = 1.52665 ν3 = 64.20 (t3)
r6 = ∞
d6 = 2.071
r7 = ∞ (SX)
d7 = 0.822
r8 = -42.111
d8 = 2.000 N4 = 1.70006 ν4 = 32.10 (t4)
r9 = 19.316
d9 = 13.451
r10 = -42.111
d10 = 2.000 N5 = 1.70006 ν5 = 32.10 (t5)
r11 = 19.316
d11 = 19.225
r12 = ∞
d12 = 7.000 N6 = 1.52665 ν6 = 64.20 (a1)
r13 = -25.950
d13 = 65.706
r14 = 155.040
d14 = 4.000 N7 = 1.52665 ν7 = 64.20 (a2)
r15 = ∞
d15 = 44.038
r16 = ∞
d16 = 5.000 N8 = 1.52665 ν8 = 64.20 (a3)
r17 = ∞
d17 = 182.653
r18 = ∞ (SY)
d18 = 70.024
r19 = ∞
d19 = 6.000 N9 = 1.52665 ν9 = 64.20 (a4)
r20 = ∞
d20 = 5.903
r21 = 129.200
d21 = 4.500 N10 = 1.52665 ν10 = 64.20 (a5)
r22 = ∞
《実施例3の短軸方向データ》
β=-0.5,NA=0.025,S1=-28.174,λ=436
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -34.868
d1= 5.800 N1= 1.76502 ν1= 44.78(t1)
r2= -22.674
d2= 0.300
r3= 37.278
d3= 6.470 N2= 1.50036 ν2= 83.58(t2)
r4= -50.107
d4= 3.461
r5= 15.570
d5= 5.600 N3= 1.52665 ν3= 64.20(t3)
r6= ∞
d6= 2.071
r7= ∞(SX)
d7= 0.822
r8= -42.111
d8= 2.000 N4= 1.70006 ν4= 32.10(t4)
r9= 19.316
d9= 13.451
r10= -42.111
d10= 2.000 N5= 1.70006 ν5= 32.10(t5)
r11= 19.316
d11=19.225
r12= ∞
d12= 7.000 N6= 1.52665 ν6= 64.20(a1)
r13= ∞
d13=65.706
r14= ∞
d14= 4.000 N7= 1.52665 ν7= 64.20(a2)
r15= ∞
d15=44.038
r16= ∞
d16= 5.000 N8= 1.52665 ν8= 64.20(a3)
r17= -77.850
d17=182.653
r18= ∞(SY)
d18= 70.024
r19= 31.140
d19= 6.000 N9= 1.52665 ν9= 64.20(a4)
r20= ∞
d20= 5.903
r21= ∞
d21= 4.500 N10=1.52665 ν10=64.20(a5)
r22= ∞
<< Short Axis Data of Example 3 >>
β = -0.5, NA = 0.025, S1 = -28.174, λ = 436
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -34.868
d1 = 5.800 N1 = 1.76502 ν1 = 44.78 (t1)
r2 = -22.674
d2 = 0.300
r3 = 37.278
d3 = 6.470 N2 = 1.50036 ν2 = 83.58 (t2)
r4 = -50.107
d4 = 3.461
r5 = 15.570
d5 = 5.600 N3 = 1.52665 ν3 = 64.20 (t3)
r6 = ∞
d6 = 2.071
r7 = ∞ (SX)
d7 = 0.822
r8 = -42.111
d8 = 2.000 N4 = 1.70006 ν4 = 32.10 (t4)
r9 = 19.316
d9 = 13.451
r10 = -42.111
d10 = 2.000 N5 = 1.70006 ν5 = 32.10 (t5)
r11 = 19.316
d11 = 19.225
r12 = ∞
d12 = 7.000 N6 = 1.52665 ν6 = 64.20 (a1)
r13 = ∞
d13 = 65.706
r14 = ∞
d14 = 4.000 N7 = 1.52665 ν7 = 64.20 (a2)
r15 = ∞
d15 = 44.038
r16 = ∞
d16 = 5.000 N8 = 1.52665 ν8 = 64.20 (a3)
r17 = -77.850
d17 = 182.653
r18 = ∞ (SY)
d18 = 70.024
r19 = 31.140
d19 = 6.000 N9 = 1.52665 ν9 = 64.20 (a4)
r20 = ∞
d20 = 5.903
r21 = ∞
d21 = 4.500 N10 = 1.52665 ν10 = 64.20 (a5)
r22 = ∞
《実施例4の長軸方向データ》
β=-7.3,NA=0.025,S1=-24.105,λ=436
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -34.868
d1= 5.800 N1= 1.76502 ν1= 44.78(t1)
r2= -22.674
d2= 3.479
r3= 37.278
d3= 6.470 N2= 1.50036 ν2= 83.58(t2)
r4= -50.107
d4= 0.650
r5= 15.570
d5= 5.600 N3= 1.52665 ν3= 64.20(t3)
r6= ∞
d6= 2.475
r7= ∞(SX)
d7= 1.155
r8= -42.111
d8= 2.000 N4= 1.70006 ν4= 32.10(t4)
r9= 19.316
d9= 7.358
r10= -42.111
d10= 2.000 N5= 1.70006 ν5= 32.10(t5)
r11= 19.316
d11=18.032
r12= ∞
d12= 7.000 N6= 1.52665 ν6= 64.20(a1)
r13= -25.950
d13= 1.161
r14= 103.360
d14= 5.000 N7= 1.52665 ν7= 64.20(a2)
r15= ∞
d15=105.837
r16= ∞
d16= 5.000 N8= 1.52665 ν8= 64.20(a3)
r17= ∞
d17=152.871
r18= ∞(SY)
d18= 71.725
r19= ∞
d19= 6.000 N9= 1.52665 ν9= 64.20(a4)
r20= ∞
d20= 6.390
r21= 103.360
d21= 5.000 N10=1.52665 ν10=64.20(a5)
r22= ∞
<< Long-axis data of Example 4 >>
β = -7.3, NA = 0.025, S1 = -24.105, λ = 436
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -34.868
d1 = 5.800 N1 = 1.76502 ν1 = 44.78 (t1)
r2 = -22.674
d2 = 3.479
r3 = 37.278
d3 = 6.470 N2 = 1.50036 ν2 = 83.58 (t2)
r4 = -50.107
d4 = 0.650
r5 = 15.570
d5 = 5.600 N3 = 1.52665 ν3 = 64.20 (t3)
r6 = ∞
d6 = 2.475
r7 = ∞ (SX)
d7 = 1.155
r8 = -42.111
d8 = 2.000 N4 = 1.70006 ν4 = 32.10 (t4)
r9 = 19.316
d9 = 7.358
r10 = -42.111
d10 = 2.000 N5 = 1.70006 ν5 = 32.10 (t5)
r11 = 19.316
d11 = 18.032
r12 = ∞
d12 = 7.000 N6 = 1.52665 ν6 = 64.20 (a1)
r13 = -25.950
d13 = 1.161
r14 = 103.360
d14 = 5.000 N7 = 1.52665 ν7 = 64.20 (a2)
r15 = ∞
d15 = 105.837
r16 = ∞
d16 = 5.000 N8 = 1.52665 ν8 = 64.20 (a3)
r17 = ∞
d17 = 152.871
r18 = ∞ (SY)
d18 = 71.725
r19 = ∞
d19 = 6.000 N9 = 1.52665 ν9 = 64.20 (a4)
r20 = ∞
d20 = 6.390
r21 = 103.360
d21 = 5.000 N10 = 1.52665 ν10 = 64.20 (a5)
r22 = ∞
《実施例4の短軸方向データ》
β=-0.5,NA=0.025,S1=-24.105,λ=436
[曲率半径] [軸上面間隔] [屈折率] [アッベ数]
r1= -34.868
d1= 5.800 N1= 1.76502 ν1= 44.78(t1)
r2= -22.674
d2= 3.479
r3= 37.278
d3= 6.470 N2= 1.50036 ν2= 83.58(t2)
r4= -50.107
d4= 0.650
r5= 15.570
d5= 5.600 N3= 1.52665 ν3= 64.20(t3)
r6= ∞
d6= 2.475
r7= ∞(SX)
d7= 1.155
r8= -42.111
d8= 2.000 N4= 1.70006 ν4= 32.10(t4)
r9= 19.316
d9= 7.358
r10= -42.111
d10= 2.000 N5= 1.70006 ν5= 32.10(t5)
r11= 19.316
d11=18.032
r12= ∞
d12= 7.000 N6= 1.52665 ν6= 64.20(a1)
r13= ∞
d13= 1.161
r14= ∞
d14= 5.000 N7= 1.52665 ν7= 64.20(a2)
r15= ∞
d15=105.837
r16= ∞
d16= 5.000 N8= 1.52665 ν8= 64.20(a3)
r17= -67.470
d17=152.871
r18= ∞(SY)
d18= 71.725
r19= 31.140
d19= 6.000 N9= 1.52665 ν9= 64.20(a4)
r20= ∞
d20= 6.390
r21= ∞
d21= 5.000 N10=1.52665 ν10=64.20(a5)
r22= ∞
<< Short Axis Data of Example 4 >>
β = -0.5, NA = 0.025, S1 = -24.105, λ = 436
[Curve radius] [Axis spacing] [Refractive index] [Abbe number]
r1 = -34.868
d1 = 5.800 N1 = 1.76502 ν1 = 44.78 (t1)
r2 = -22.674
d2 = 3.479
r3 = 37.278
d3 = 6.470 N2 = 1.50036 ν2 = 83.58 (t2)
r4 = -50.107
d4 = 0.650
r5 = 15.570
d5 = 5.600 N3 = 1.52665 ν3 = 64.20 (t3)
r6 = ∞
d6 = 2.475
r7 = ∞ (SX)
d7 = 1.155
r8 = -42.111
d8 = 2.000 N4 = 1.70006 ν4 = 32.10 (t4)
r9 = 19.316
d9 = 7.358
r10 = -42.111
d10 = 2.000 N5 = 1.70006 ν5 = 32.10 (t5)
r11 = 19.316
d11 = 18.032
r12 = ∞
d12 = 7.000 N6 = 1.52665 ν6 = 64.20 (a1)
r13 = ∞
d13 = 1.161
r14 = ∞
d14 = 5.000 N7 = 1.52665 ν7 = 64.20 (a2)
r15 = ∞
d15 = 105.837
r16 = ∞
d16 = 5.000 N8 = 1.52665 ν8 = 64.20 (a3)
r17 = -67.470
d17 = 152.871
r18 = ∞ (SY)
d18 = 71.725
r19 = 31.140
d19 = 6.000 N9 = 1.52665 ν9 = 64.20 (a4)
r20 = ∞
d20 = 6.390
r21 = ∞
d21 = 5.000 N10 = 1.52665 ν10 = 64.20 (a5)
r22 = ∞
AP アナモフィック光学系(結像光学系)
ti 第i回転対称レンズ
aj 第jアナモフィックレンズ
ST 絞り
SX 長軸方向絞り
SY 短軸方向絞り
1 光源
2 楕円面鏡
F1 第1焦点
F2 第2焦点
3 オプティカルインテグレータ
3a 入射端面
3b 射出端面
IM 被照射面
AX 光軸
AP Anamorphic optical system (imaging optical system)
ti i th rotationally symmetric lens aj j anamorphic lens ST stop SX long axis direction stop SY short axis direction stop 1
Claims (6)
1.90<|fXall/fsym|<20.00 …(1)
ただし、
fXall:アナモフィック光学系の長軸方向の焦点距離、
fsym:全回転対称レンズのみから成るレンズ群の焦点距離、
である。 An anamorphic optical system having at least one rotationally symmetric lens that is rotationally symmetric with respect to an optical axis and one or more anamorphic lenses that include surfaces having different curvatures in directions perpendicular to each other, and having different magnifications in directions perpendicular to each other. An anamorphic optical system characterized by satisfying the following conditional expression (1) when the direction in which the absolute value of magnification is the major axis direction and the direction in which the absolute value of magnification is the minor axis direction:
1.90 <| fXall / fsym | <20.00… (1)
However,
fXall: Focal length in the long axis direction of the anamorphic optical system,
fsym: focal length of a lens group consisting only of all rotationally symmetric lenses,
It is.
6.4<|βlong/βshort|<30.0 …(2)
ただし、
βlong:アナモフィック光学系の長軸方向の倍率、
βshort:アナモフィック光学系の短軸方向の倍率、
である。 The anamorphic optical system according to claim 1, wherein the following conditional expression (2) is satisfied:
6.4 <| βlong / βshort | <30.0 (2)
However,
βlong: magnification in the long axis direction of the anamorphic optical system,
βshort: magnification in the minor axis direction of the anamorphic optical system,
It is.
6.4<|βlong/βshort|<30.0 …(2)
ただし、
βlong:アナモフィック光学系の長軸方向の倍率、
βshort:アナモフィック光学系の短軸方向の倍率、
である。 An anamorphic optical system having at least one rotationally symmetric lens that is rotationally symmetric with respect to an optical axis and one or more anamorphic lenses that include surfaces having different curvatures in directions perpendicular to each other, and having different magnifications in directions perpendicular to each other. An anamorphic optical system characterized by satisfying the following conditional expression (2) when a direction in which the absolute value of magnification is a major axis direction and a direction in which the absolute value of magnification is a minor axis direction:
6.4 <| βlong / βshort | <30.0 (2)
However,
βlong: magnification in the long axis direction of the anamorphic optical system,
βshort: magnification in the minor axis direction of the anamorphic optical system,
It is.
1.90<|fXall/fsym|<20.00 …(1)
ただし、
fXall:アナモフィック光学系の長軸方向の焦点距離、
fsym:全回転対称レンズのみから成るレンズ群の焦点距離、
である。 The anamorphic optical system according to claim 3, wherein the following conditional expression (1) is satisfied:
1.90 <| fXall / fsym | <20.00… (1)
However,
fXall: Focal length in the long axis direction of the anamorphic optical system,
fsym: focal length of a lens group consisting only of all rotationally symmetric lenses,
It is.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2003324072A JP2005091660A (en) | 2003-09-17 | 2003-09-17 | Anamorphic optical system |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2003324072A JP2005091660A (en) | 2003-09-17 | 2003-09-17 | Anamorphic optical system |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| JP2005091660A true JP2005091660A (en) | 2005-04-07 |
Family
ID=34454928
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2003324072A Pending JP2005091660A (en) | 2003-09-17 | 2003-09-17 | Anamorphic optical system |
Country Status (1)
| Country | Link |
|---|---|
| JP (1) | JP2005091660A (en) |
Cited By (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2013045109A (en) * | 2011-08-24 | 2013-03-04 | Palo Alto Research Center Inc | Single-pass imaging system using spatial light modulator and catadioptric anamorphic optical system |
| JP2013050716A (en) * | 2011-08-24 | 2013-03-14 | Palo Alto Research Center Inc | Single-pass imaging system with anamorphic optical system |
-
2003
- 2003-09-17 JP JP2003324072A patent/JP2005091660A/en active Pending
Cited By (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2013045109A (en) * | 2011-08-24 | 2013-03-04 | Palo Alto Research Center Inc | Single-pass imaging system using spatial light modulator and catadioptric anamorphic optical system |
| JP2013050716A (en) * | 2011-08-24 | 2013-03-14 | Palo Alto Research Center Inc | Single-pass imaging system with anamorphic optical system |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP2000009997A (en) | Zoom lens | |
| JP2004085600A (en) | Wide angle zoom lens system | |
| JP4776948B2 (en) | Variable magnification optical system | |
| JPH05203874A (en) | Telecentric image formation optical system | |
| JP2004070092A (en) | Zoom photography optical system | |
| JP2000089110A (en) | Zoom lens | |
| JP4634578B2 (en) | Endoscope objective variable magnification optical system | |
| JP2014102426A (en) | Zoom lens and image projection device having the same | |
| US8482862B2 (en) | Variable power optical system for stereomicroscope | |
| JP3309998B2 (en) | Compact zoom lens | |
| KR20020062779A (en) | A zoom lens system | |
| JP4380158B2 (en) | Zoom lens | |
| JPH116958A (en) | Zoom lens | |
| JP2000275524A (en) | Zoom lens | |
| JP2007052273A (en) | Zoom lens | |
| JP2005091660A (en) | Anamorphic optical system | |
| JP2009053326A (en) | Zoom lens | |
| JP3984231B2 (en) | Zoom lens | |
| JP2004037921A (en) | Zoom lens system | |
| JPH08262325A (en) | Zoom lens | |
| US20020097503A1 (en) | Zoom lens system | |
| JP2004133338A (en) | Projection lens for projector | |
| JP6355414B2 (en) | Optical system and image projection apparatus having the same | |
| JP6296724B2 (en) | Zoom lens and image projection apparatus having the same | |
| US6282035B1 (en) | Image forming optical system in which the effects of ghosting are minimized |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A711 | Notification of change in applicant |
Effective date: 20050615 Free format text: JAPANESE INTERMEDIATE CODE: A712 |
|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20050622 |