- Text
- Chapter
- El Colegio de México
- pp. 1-46
-
- View Citation
- Additional Information
1. Introducción
Los objetivos centrales de este trabajo son dos: i) establecer un conjunto de principios que nos permitan traducir a modelos matemáticos las proposiciones teóricas que originan variables cualitativas y ii) analizar los problemas de ajuste que se encuentran involucrados en su estimación.
Veamos un poco más de cerca ambos propósitos. El primero dice relación directa con un cambio de lenguaje. En efecto, la formalización puede ser vista como un problema de traducción a términos matemáticos de las hipótesis teóricas, las que normalmente en las ciencias sociales son expresadas en lenguaje natural. Pero no nos interesa cualquier tipo de formalización sino aquel que origina un modelo matemático en que los factores explicativos son cualitativos. Otra restricción a este primer objetivó del trabajo se refiere a que sólo nos preocuparemos por aquel tipo de proposiciones teóricas que dan pie a la construcción de modelos uniecuacionales y lineales o susceptibles de ser linealizados.
En consecuencia nuestro interés es bastante limitado por cuanto se restringe a sólo aquellas hipótesis teóricas que: i) sean susceptibles de ser traducidas a un lenguaje matemático (aquellas que no se puedan llevar al campo de las matemáticas no tienen cabida en este escrito), ii) que el modelo así construido sea uniecuacional y posible de ser llevado a la forma lineal y iii) que todos o algunos de los factores explicativos sean de naturaleza cualitativa.
Para estimar el modelo matemático (segundo objetivo central de este trabajo) es necesario asociarle un modelo estadístico que incorpore los parámetros característicos del primero. Los requisitos que hemos perfilado para el tipo de ecuación que nos preocupa, tienen su correspondencia estadística inmediata en el modelo de regresión lineal, pero no se trataría del modelo ordinario sino de uno que tiene la particularidad de incorporar variables cualitativas.
Lo anterior entra en abierta contradicción con lo sostenido en algunos libros de texto que han tenido amplia repercusión1 los cuales han difundido la noción que postula que una de las limitaciones más importantes en la aplicación del modelo de regresión a los problemas característicos de las ciencias sociales radicaría en el nivel de medición de las variables: sólo se podría estimar una ecuación de regresión si todas y cada una de sus variables han sido expresadas a nivel métrico.
Dentro de esta línea argumental es que se promueve el uso del análisis de asociación y de covarianzas de Lazarsfeld en aqúellos casos en que las variables son nominales u ordinales. La construcción y estimación de modelos de regresión que incorporan variables cualitativas (normalmente denominadas mudas o ficticias y que corresponden al vocablo inglés dummy) pueden ser pensadas como una manera alternativa de analizar el grado de relación que une a dos o más variables. El intento de reemplazar un tipo de instrumento estadístico por otro encuentra su justificación en el mayor poder analítico que caracteriza al modelo de regresión.
En cuanto a la estrategia de exposición hemos decidido destacar en las primeras secciones el enlace entre el pensamiento teórico y su expresión matemática. Para ello supondremos la existencia de hipótesis sustantivas que orienten la descomposición de la variable explicada2 en términos de los factores explicativos y a partir de ella preguntarnos por la ecuación matemática y el modelo de regresión que mejor la refleja. Desde el séptimo apartado en adelante nos dedicamos al estudio de los problemas de estimación que son característicos de los modelos de regresión con variables mudas.
Si bien en la primera parte destacamos los problemas de formalización y en la segunda los de estimación, esto no quiere decir que la separación sea taxativa, lo que acontece es que la mezcla en un momento adquiere un tono mayor de formalización y en otro una coloración menor. Además, el orden que seguiremos tiene que ver con una gradación en el orden de dificultad para acceder a la comprensión del material que se entrega. Las últimas secciones requieren que el lector posea un cierto nivel de formación previa en inferencia estadística y en algunos tópicos econométricos, en tanto que las primeras sólo exigen una lectura atenta y detenida.
2. Estimación de la función escalonada
Con el objeto de darle contenido al problema que abordaremos, supongamos que un analista social, después de una serie de operaciones teóricas, llega a establecer que existe una relación entre el grado de urbanización y el volumen de producción industrial. La vinculación entre estas variables descansa en la noción de que las calidades asociadas al espacio físico condicionarían la actividad industrial. En este sentido pareciera ser evidente el papel que juegan las disponibilidades de servicios fundamentales como por ejemplo, energía eléctrica, agua, etc., así como las facilidades de comunicación física con el ambiente exterior, en todo lo que tiene que ver con el movimiento de los insumos y los productos terminados.
Esta aseveración de carácter general se especifica en el momento en que el investigador sostiene que, si bien esta relación existe, ella no es continua. Vale decir, entre determinados niveles de urbanización, la producción industrial es relativamente constante, pero a partir de cierto punto, o de cierto grado de urbanización en adelante, la producción industrial sufre un aumento manteniéndose constante hasta que alcanza otro punto, donde nuevamente experimenta una modificación importante. Este proceso se repite un gran número de veces.
La expresión gráfica correspondiente a esta forma de pensamiento es: donde el eje de abscisas mide el grado de urbanización (X) y, el de las ordenadas, el volumen de la producción (Y)3, expresada en términos per cápita.
La función representada en la gráfica se denomina función escalonada y sirve para expresar matemáticamente una situación perfectamente general. Al establecer clases estadísticas se introducen dos elementos que las caracterizan: i) como mínimo un cierto nivel de homogeneidad interna con respecto a la variable que nos interesa y ii) un cierto grado de diferenciación entre ellas.
En otras palabras, se puede hablar de una clase estadística en la medida que la variabilidad intraclase sea mínima a la vez que la interclase sea significativa. Aun cuando generalmente se requiere de más de una característica o variable para definir una clase estadística, supondremos, en un comienzo, que ello es posible haciendo uso de sólo una variable. Posteriormente complicaremos el análisis.
Definido el problema en estos términos, tenemos dos alternativas para ajustar una función a la gráfica en cuestión.
Una de ellas consiste en ajustar a las observaciones un polinomio de grado elevado.4 Normalmente esta solución tiene un alto costo en términos de grados de libertad, lo que no la hace aconsejable. La otra alternativa es la de usar variables mudas (dummy), la cual, como veremos más adelante, si bien también tiene un costo en términos de grados de libertad, en la mayoría de los casos es bastante menor que el que hay que pagar cuando se ajusta un polinomio.
Para el caso en que tenemos tres clases o categorías (ver gráfica) definidas de la manera siguiente:
Clase A, está formada por todos aquellos X, tales que:
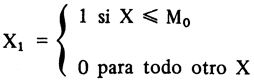
Clase B, formada por todas las observaciones en que:

Clase C, se define para todo X, tal que
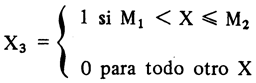
abordaremos el problema de ajuste postulando un modelo de regresión lineal múltiple. En concreto se trata de ajustar la función:

en que el término e simboliza el error estocástico y se agrega al valor esperado para dar cuenta de la variabilidad intraclase. Por lo tanto, puede ser utilizado como un indicador del éxito o fracaso al definir las clases.5
Los supuestos clásicos respecto al término de error son:
1. E(e) = 0
2. Var(e) = σ2, donde = σ2 simboliza a la varianza y se supone constante.
3. Cov(e) = 0; es decir, ausencia de correlación entre los residuos. Si estas tres condiciones se cumplen al procedimiento más adecuado de ajuste es el mínimo cuadrático ordinario. Pero antes de avanzar en esta dirección hagamos uso del supuesto E(e) = 0 para escribir el modelo (1) en la forma:

Si suponemos que X≤M0, vale decir, X es tal que pertenece a la clase A, entonces X1 asumirá el valor 1 y, X2 y X3 tomarán valores cero. Aplicando la ecuación (2) tenemos:

donde E{Y/A}, es el valor esperado de Y dado que la observación pertenece a la clase A. Por lo tanto, β1 puede ser interpretado como el efecto esperado sobre la variable explicada, de la pertenencia a la clase A. Según este modelo cualquier observación que cumpla con la desigualdad X≤M0, tendrá el mismo impacto sobre Y, es decir, el efecto de la clase es constante. Justamente ésta es una de las propiedades básicas que caracteriza a las funciones escalonadas y que deseábamos capturar algebraicamente.
Si la observación pertenece a la clase B, entonces:

donde β2 es el efecto esperado de la pertenencia a la clase B sobre la variable industrialización.
Del mismo modo se tiene: E{Y/C} = β3 donde β3 es el efecto de pertenencia a la clase C.
Estos resultados implican que en el ejemplo que hemos usado como ilustraciónβ1 es el efecto del primer nivel de urbanización sobré la industrialización; β2 simboliza el impacto del segundo nivel; β3 es el del tercer nivel. Por analogía se puede extender el procedimiento sobre cualquier número de clases. La única limitación para el ajuste radicará en las disponibilidades de información numérica.
Las ecuaciones normales que se deben calcular para realizar el ajuste son:

Sabemos por la manera en que hemos definido las variables mudas que para todos los X pertenecientes a la clase A, X1 = 1, en tanto que X2 = X3 = 0. Al aplicar estas condiciones sobre las ecuaciones tenemos que la primera se transforma en:
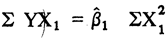
mientras que la segunda y tercera se hacen iguales a cero. Las sumatorias de ella se extienden sobre todos los X, que pertenecen a la clase estadística A. Si suponemos que el tamaño de esta clase es NA tendremos:

debido a que X1 = 1, por lo tanto, 

En el caso que se trabaje con las observaciones correspondientes a la clase B, la segunda ecuación normal toma la forma:
mientras que la primera y tercera ecuaciones se hacen idénticamente iguales a cero.
Por medio de un procedimiento análogo se llega a:

En conclusión los estimadores mínimos-cuadráticos de los efectos de pertenencia a clase son las medias aritméticas de la variable explicada en cada clase.
Como la ecuación (1) no incluye un término libre y es usual que cualquier modelo de regresión sí lo incorpore, supongamos que se introduce en el modelo de la forma siguiente:

en que X0 es siempre igual a 1. Luego, esta misma ecuación puede asumir la siguiente forma:

En este caso la inclusión del término libre nos crea un problema bastante serio, por cuanto, siempre se cumplirá que:

lo que genera un problema denominado técnicamente “multicolinealidad” que en esencia se traduce en que las ecuaciones normales no sean linealmente independientes y, por consiguiente tenemos más incógnitas que ecuaciones, por lo que no es posible determinar los estimadores mínimo-cuadráticos.
Luego, al ajustar una función escalonada no se debe incluir un término libre.
Un lector inquieto puede preguntarse acerca de la dependencia de los resultados encontrados respecto a la forma de definición de las variables. Es claro que, aun cuando se acepte las variables dicotómicas como una forma de simbolizar presencia o ausencia de atributos hay varias formas de definirlas. Con el propósito de estudiar la sensibilidad de los resultados respecto a la manera como se definen las variables mudas consideremos que:

En este caso, aún sigue siendo válida la ecuación (1) y sus correspondientes ecuaciones normales. Sin embargo, hay que recordar que el regresor6 X1 es igual a 1, para todas las clases. Este hecho nos introduce una ligera modificación sobre las ecuaciones normales.
Al reemplazar estos nuevos valores de las variables mudas en las sumatorias constituyentes de las ecuaciones normales obtenemos:
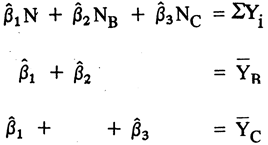
donde N representa el total de las observaciones, mientras que NB y NC simbolizan los tamaños de las clases B y C respectivamente.
Resolviendo el sistema de ecuaciones se llega a:

Al comparar estas ecuaciones con las que obtuvimos a partir del primer conjunto de variables mudas pareciera concluirse que las estimaciones que se obtengan dependerán de la manera como se definan las variables. Si los resultados variasen de acuerdo con el conjunto arbitrario de definiciones, los procedimientos señalados gozarían de un dudoso valor aplicado. Sin embargo, las expresiones aparentemente distintas que asumen los estimadores mínimos cuadráticos en uno y otro caso se debe a que están midiendo “cosas” diferentes. Como consecuencia los resultados deben ser distintos. En efecto, el primer conjunto de variables mudas mide el impacto absoluto de cada clase estadística sobre la variable explicada, mientras que el segundo mide el impacto relativo, tomando como base de comparación la primera clase.
Las definiciones utilizadas en el primer conjunto de variables mudas conducen a que los estimadores mínimos cuadráticos de la ecuación de regresión midan las alturas dela siguiente gráfica.
en tanto que, con el segundo conjunto se mide el efecto diferencial de cada categoría, comparada con la primera tal como se señala en la siguiente gráfica:

En el caso que la interpretación gráfica que hemos expuesto sea correcta al sumar β^1 y β^2 obtenidas a partir del segundo conjunto de variables mudas, debe llegarse al mismo resultado que el de β^2 calculado sobre la base de las definiciones del primer conjunto de variables ficticias. Lo mismo debe ocurrir al sumar β^1 a β^2 para el segundo conjunto. Es decir, la suma tiene que ser igual al β^3, correspondiente a las primeras definiciones.
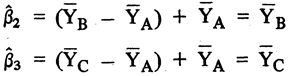
Por consiguiente, podemos concluir que si aceptamos representar presencia o ausencia de atributos por medio de variables dicotómicas, entonces los resultados de las estimaciones pueden variar pero sólo en el caso que se estén midiendo efectos distintos.
Supongamos que para estudiar el impacto de la urbanización sobre la industrialización, tricotomizamos la primera variable en los niveles bajo, medio y alto. Por lo tanto, nuestra medición se hará sobre unidades geográficas que se clasificarán por urbanización en una de las tres categorías. Esperamos que el nivel de industrialización correspondiente a cada categoría de la variable X sea similar. Es decir, que los niveles de desarrollo industrial sólo se diferencien en términos de factores aleatorios.
El primer conjunto de variables mudas nos lleva a interpretar los valores de los estimadores mínimo-cuadráticos como el efecto absoluto de cada una de las categorías de la variable urbanización. El segundo conjunto, muestra el impacto diferencial (o relativo) de los niveles medio y alto, en comparación al del nivel bajo. La elección de la base de comparación es arbitraria, también podríamos haber elegido la categoría media o la alta, pero, lo que no es arbitrario es la definición de las variables para cada caso.
3. Estimación de un modelo de regresión con dos variables explicativas cualitativas
Supongamos que una vez que nuestro investigador ha aplicado la técnica expuesta en la sección 2, no se encuentra satisfecho con los resultados obtenidos. La variabilidad intraclase es demasiado grande y, por lo tanto, el coeficiente de determinación es bajo.
Planteado el problema ha revisado su esquema teórico y después de un análisis detenido decide incluir una variable clasificatoria adicional.
En términos estadísticos esto significa que no se ha tenido éxito en definir las clases. La variabilidad interna es demasiado grande. La constitución del estrato depende de más de una variable.
La decisión del teórico es la de incluir la variable región. Su argumento básico es que el uso de los servicios necesarios para la producción, es una función de las disponibilidades de recursos de cada región. Para simplificar la exposición supongamos que este país se caracteriza porque la zona norte es esencialmente minera, la zona central es un complejo de actividades mineras, agrícolas, de servicios, e industriales. La zona sur es esencialmente agrícola.
En resumen, se pretende explicar o estimar el impacto que tiene sobre el nivel de industrialización la urbanización condicionada por la región en la cual se desarrolla. En este momento nuestro investigador necesita elaborar un poco más su esquema teórico. Veremos que la técnica en sí plantea algunas interrogantes que reenvían sobre la teoría realizando preguntas muy específicas.
La forma típica de presentación de la información, es una tabla como la siguiente:
La variable Y simboliza el nivel de industrialización. El subíndice k, es variable por cuanto el número de observaciones por casillas es distinto y es igual a n1 para la primera; n2 para la segunda y así sucesivamente llegar a n9 para la última casilla. Además se cumple que;

Para estar en condiciones de continuar con el análisis es necesario preguntar respecto a la forma de concebir el impacto de las variables. ¿Sus impactos son agregativos?; ¿son interactivos? Si son interactivos, ¿Dónde o a qué niveles se produce la interacción?, etc. Es claro que las respuestas deben buscarse al nivel teórico haciendo uso de los conocimientos disponibles. En todo caso, lo que nos interesa en este trabajo es exponer algunas alternativas de análisis y por consiguiente, supondremos que la técnica estadística es capaz de abrir un abanico de posibilidades.
Caso 1: Un modelo agregativo simple
Supongamos que se argumenta que el impacto de la urbanización sobre la industrialización es el mismo en cualquier región y que esto también es válido para la variable región, es decir, que el efecto de los recursos y calidades espaciales sobre la producción industrial es independiente del nivel de urbanización que haya alcanzado cada unidad geográfica.
En virtud de estas consideraciones podemos construir una tabla en que se expresen los efectos esperados de las variables explicativas sobre la explicada:
β1 representa el nivel de industrialización esperado en las localidades con bajos niveles de urbanización y que además se encuentran situadas en la zona norte. Esta categoría es la que se usa como base de comparación.
Si restamos a la segunda línea la primera, nos encontramos con que para los tres pares de casillas dicha diferencia es igual a β2. Ello significa que este parámetro indica el impacto relativo asociado a la categoría centro. Manteniendo constante el nivel de urbanización, esperamos un efecto igual a β2, por el hecho de que la localidad se encuentre en la zona central en lugar de la zona norte. Además, suponemos que este impacto es independiente del nivel de urbanización. El parámetro β2 es el mismo para cualquier nivel de urbanización.
Una interpretación similar se puede realizar para β3 ; β3es un parámetro que captura el efecto relativo de la zona sur sobre el nivel de industrialización. Relativo porque se toma como base de comparación la zona norte. β4, se puede obtener restando a la segunda columna la primera. Por lo tanto, permite representar el efecto relativo de la clase estadística urbanización media, sobre el nivel de industrialización. Sin embargo, en este caso usamos como base de comparación el nivel bajo de urbanización. Por otra parte como β4 es el mismo para cualquier región, entonces el nivel de urbanización es independiente de la región.
El parámetro β5, se interpreta de manera similar que β4. Es decir, representa el impacto relativo del grado alto de urbanización sobre la industrialización. La base de comparación es el nivel bajo de la misma variable.
En esta forma de descomponer la variable explicada o a explicar, hemos realizado dos supuestos básicos: 1) la variable industrialización se puede descomponer en una serie de factores agregativos; 2) el impacto de la variable explicativa urbanización es independiente del nivel de la variable regionalización. La aseveración inversa también es válida.
Estas afirmaciones son supuestos para la construcción del modelo. Sin embargo, desde el punto de vista teórico constituyen hipótesis a demostrar. Normalmente, estas hipótesis son o deben ser obtenidas con base en el desarrollo del esquema teórico.
Una vez establecido el modelo que descompone la variable industrialización en una serie de electos simbolizados por los distintos valores de β, debemos proceder a la estimación de ellos.
A continuación examinaremos la manera como podemos pasar desde la descomposición teórica de la variable explicada (que se ha expuesto en la tabla) a una ecuación de regresión. Con este propósito consideremos:

Si el primer elemento del par ordenado (i, j) simboliza las líneas y el segundo las columnas entonces cuando una observación cae en la casilla (1,1) las variables asumen los siguientes valores:

Al reemplazarlos en la ecuación (3) tenemos:

Este resultado es idéntico con el de la casilla (1,1), de la tabla en que se descompone la variable urbanización en “efectos”.
En consecuencia el modelo estadístico representará adecuadamente el efecto esperado de las variables explicativas sobre la explicada en la casilla (1,1) si asignamos ese conjunto de valores a cada unidad geográfica que cumpla con las características de nivel bajo de urbahización y que se ubique en la zona norte.
Al establecer las correspondencias entre la ecuación de regresión y la déscomposición en efectos desarrollada en la tabla, encontramos que el conjunto típico de valores que tendremos que asignar a las distintas variables para lograr una equivalencia exacta en cada una de las casillas deben ser:

Para realizar el ajuste mínimo-cuadrático disponemos de un conjunto n de valores de variables en que habrá n1 iguales a la primera línea de la tabla, n2 iguales a la segunda línea y así hasta n9 iguales a la de la última línea de la tabla.
Con el listado correspondiente a las variables explicativas y explicada, podemos aplicar los procedimientos tradicionales de estimación mínimo-cuadrática, obteniéndose de ese modo las estimaciones de los parámetros.
Caso 2: La interacción en modelos agregativos:
Consideremos a continuación el caso en que no existe independencia entre las variables explicativas, urbanización y regionalización. Supongamos que desde el punto de vista teórico se establece que para todas aquellas unidades geográficas que se encuentran en la zona central y, que poseen un nivel medio de urbanización, la variable industrialización está compuesta no sólo por los impactos individuales de cada variable sino que también hay que considerar un efecto inducido por la conjunción de ambas categorías.
En este caso la tabla teórica de descomposición de la variable explicada (industrialización) asume la siguiente forma:

La única diferencia con la tabla que refleja la descomposición de la variable producción industrial en el caso 1 radica en que en ésta hemos agregado un coeficiente(β6) que representa el impacto sobre la industrialización de la interacción entre las categorías zona central y urbanización media. Para incorporar este nuevo componente en el modelo de regresión debemos incluir un nuevo parámetro (β6,) asociado a una nueva variable muda (X6) que asumirá el valor 1 en la casilla (2,2) y el valor cero en todas las demás. Por lo tanto, el modelo adquiere ahora la siguiente forma:
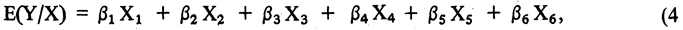
y el listado de las observaciones típicas será:
En el modelo de regresión comúnmente utilizado (es decir aquel en que todas las variables explicativas son métricas) se acostumbra representar la interacción por medio del producto de dos o más variables. Nótese que lo mismo acontece cuando el modelo contiene variables cualitativas: X6 podría haber sido definida como X2X4.
Siguiendo un procedimiento similar al expuesto se podría continuar considerando interacciones entre las distintas categorías. El límite estará dado por un modelo en que se considere interacciones entre todos los niveles de las variables. Si deseamos trabajar con esteorden de generalidad no hay razones para considerar el conjunto de observaciones como si fuesen una sola unidad. En este caso lo más conveniente es trabajar cada casilla de manera separada utilizando la técnica expuesta en la sección 2.
Si bien los cases expuestos sólo constituyen un par de ejemplos tomados entre un sinnúmero de maneras de descomponer la variable explicada (industrialización), pensamos que en el transcurso de la exposición hemos sentado principios relativamente generales7 que nos permiten establecer una correspondencia entre una tabla en que se expresa la descomposición teóricamente esperada de la variable explicada y un modelo de regresión.
En el próximo apartado nos preocuparemos por aplicar esos principios a la construcción, análisis y estimación de modelos en que la variable explicada es una proporción o un porcentaje. Este caso amerita un tratamiento particular en la medida que se levanta como un instrumento analíticamente más potente que el tan popular análisis de asociación o de porcentajes.
4. Una alternativa al análisis porcentual
En la sección anterior hemos considerado el caso en que la variable explicada es métrica. En ésta estudiaremos la forma de plantear el modelo cuando la variable Y es dicotómica y se sustituye por una variable cuantitativa, al definirla en términos de proporciones o porcentajes. Además de plantear algunos modelos alternativos de análisis, los cuales deben ser entendidos como complementarios a los desarrollados en la sección anterior, consideraremos los problemas de estimación que son característicos en este tipo de módelos.
Con el propósito de adscribir un cierto contenido sustantivo a las ideas estadísticas que entregaremos usaremos un ejemplo tomado de la sociodemografía. Creemos que no está demás señalar que por no ser éste un trabajo de naturaleza teórica, sólo presentaremos una versión extremadamente reducida de los planteamientos teóricos. Esto lleva implícito el riesgo de entregar una caricatura de cada postura sustantiva, pero tiene la virtud de focalizar lo medular de la formalización, cuestión que sí constituye uno de nuestros objetivos centrales.
4.1. Un breve resumen de una teoría
Para intentar explicar la migración rural-urbana se dispone de algunas nociones teóricas las cuales se pueden sintetizar en ideas relativas al grado de modernismo del campesino, consideraciones de carácter estructural y, por último, factores particulares de expulsión de mano de obra campesina.
La conclusión última del primer enfoque es que la tasa de migración es mayor a medida que mayor es el nivel de modernización del campesino. El enfoque estructural establece que la proporción de migrantes potenciales depende de las relaciones de producción y de las relaciones sociales que se establecen al interior de la explotación agrícola. En concreto, si ha existido un proceso de reforma agraria que ha producido cambios estructurales y observamos las tasas o proporciones de migración al interior del área reformada éstas serán sustancialmente menores que las de las explotaciones agrícolas tradicionales.
Por otra parte la investigación de Omar Argüello8 establece que el grado de modernización de los campesinos afecta a la migración en aquellos contextos sociales que no han sufrido cambios estructurales. Mientras que las variaciones estructurales juegan un papel fundamental en la explicación de la migración cuando se han llevado a cabo reales procesos de Reforma Agraria.
Además de estas ideas, existen otras explicaciones en que se considera el papel de variables aisladas. Por ejemplo, se plantea que el nivel de ingreso o que la educación, etc., juegan un “papel”. Para nuestros objetivos consideraremos que la migración potencial puede ser explicada por las características estructurales de la explotación agrícola; por el grado de modernización del campesino y por el nivel de ingreso.
En relación a los factores estructurales distinguiremos dos categorías; a saber, explotaciones pertenecientes al área no reformada y reformada. La variable modernización será dicotomizada en moderno y no moderno y consideraremos tres niveles de ingreso: alto, medio y bajo. La variable a explicar es la proporción de migrantes potenciales.
4.2. Algunos modelos
Tal vez algunos de los modelos ya presentados podrían revelarse útiles para el análisis de la migración. Sin embargo para los propósitos de este trabajo preferimos plantear otras maneras de descomponer la variable explicada. A estos efectos permítasenos considerar el siguiente esquema de descomposición de la variable a ser explicada:
El parámetro β1 representa el efecto absoluto sobre la migración potencial de las categorías área no reformada, nivel de ingreso bajo y modernismo de los campesinos. El valor de él se usa como base de comparación.
β2 y, β3 toman én cuenta el impacto relativo de los niveles de ingreso medio y alto respectivamente sobre la migración potencial, y se caracterizan por ser independientes del tipo de explotación productiva agrícola.
β12 nos indica el efecto esperado de la caída del nivel de modernización en el área no reformada sobre la migración.
Al interior del área reformada, se siguen manteniendo los efectos agregativos del nivel de ingresos. Sin embargo, el impacto de la categoría “área reformada” sobre la migración potencial es diferencial dependiendo del nivel de modernismo del campesino. En efecto, el área reformada produce un impacto diferente si interactúa con la categoría moderno, que si lo hace con la de no moderno. En el primer caso dicho impacto es β21 y, en el segundo β22.
Siguiendo un procedimiento similar al empleado en la sección anterior podemos establecer el modelo:

en que el listado exhaustivo de las variables es como se muestra en la tabla siguiente.
Desde el punto de vista de la estimación, este modelo presenta una importante diferencia respecto a los anteriormente expuestos: en lugar de que el número de casos sea igual a la cantidad de observaciones realizadas resulta ser igual al número de casillas de la tabla, lo que implica una reducción en los grados de libertad con los que se realiza el ajuste. En efecto en la tercera sección trabajamos con un conjunto de n observaciones, pero al considerar las proporciones asociadas a cada casilla nos movemos desde una situación en que para llevar a cabo la estimación contábamos con n observaciones a una en que el n resulta ser el total de celdas de la tabla. En el ejemplo que estamos utilizando, el número de observaciones es 12 independientemente de la cantidad de unidades que constituyen la muestra.
Por otra parte, el ajuste mínimo-cuadrático presenta algunas complicaciones que estudiaremos en el próximo apartado.
Con el propósito de presentar otras maneras de descomponer una variable, supongamos que el investigador establece que la proporción de migrantes potenciales sigue el esquema representado por la tabla siguiente:

en que las interpretaciones para β1, β2 y β3 son las mismas que en el caso anterior. La diferencia entre esta manera de descomponer la variable explicada y la recién expuesta estriba en los términos del tipo α Ύ
Según este modelo de descomposición de la migración potencial, el parámetro Ύ1, puede interpretarse como el efecto del nivel de modernización del campesinado. Sin embargo, su impacto final depende del contexto productivo en que opera, ya que hemos supuesto que en el área no reformada actúa sobre un nivel α1 en tanto que en el área reformada, sobre un nivel α2, el cual se caracteriza por ser distinto a α1. La diferencia entre casillas análogas, definidas en los dos tipos de contextos productivos, nos muestra que para el mismo nivel de modernización e ingresos se cumple que (α1 — α2) Ύ1, es decir, el impacto del tipo de organización productiva sobre la migración potencial, está condicionado por el hecho de que el campesino presente características que lleven a catalogarlo de moderno.
El Modelo se puede expresar como:
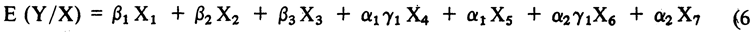
y el listado exhaustivo de las variables será:

4.3. Problemas de estimación
El tipo de modelos que hemos analizado se caracteriza por el hecho que la variable explicada está expresada en términos porcentuales o como proporciones lo que implica que su rango de variación se encuentre limitado al intervalo definido por 0 y 100 en un caso y en el otro por 0 y 1.
Para garantizar que se cumplan estos límites de variación en la estimación de la variable explicada, podemos recurrir al expediente de utilizar sólo funciones que cumplan con dicho requisito. Esta alternativa tiene un costo expresado en cantidad de funciones disponibles.9
Otra forma de lograr el mismo propósito es por medio de la transformación de la variable explicada de manera tal que desaparezcan las restricciones de recorrido. Hay varias alternativas disponibles, como la transformación probit,10 la transformación tangente y la transformación logit.11 Desde el punto de vista matemático estas tres transformaciones tienen propiedades equivalentes y en consecuencia la exposición se puede centrar en sólo una de ellas sin que se manifieste en una pérdida de generalidad. Nosotros hemos preferido de entre las tres a la transformación logit.
Sea Pij, la probabilidad correspondiente a la casilla ubicada en la i-ésima línea y j-ésima columna. El logit de Pij se define como:
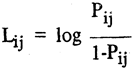
donde la razón Pij/1-Pij, mide las chances a favor de la variable en cuestión. Por ejemplo si Pij = 0.8 entonces Pij/1-Pij = 4/1.
Si P se refiere a la proporción de migrantes potenciales dicho valor nos dice que por cada 5 campesinos hay 4 dispuestos a migrar y sólo uno está en la situación contraria.
La función logit responde a la siguiente representación gráfica:

A partir de esta gráfica debemos destacar dos hechos notables: i) al realizar la transformación han desaparecido las restricciones del recorrido de la variable, el logit varía entre más y menos infinito y ii) los aumentos absolutos de la misma magnitud, en general, tienen efectos distintos sobre el logit. En la gráfica12 distancia entre 1/2 y A0, es igual a la distancia entre A1 y A2. Sin embargo, el efecto de variaciones absolutas iguales en las probabilidades, tiene efectos distintos sobre el logit: dada la forma de la función, siempre L2 será mayor que L1. Esta propiedad da contenido a la idea de que los aumentos porcentuales de un mismo tamaño tienen sentido distinto dependiendo del nivel sobre el cual se aplican. Un aumento del 3%, tiene una importancia relativa menor cuando se produce a consecuencia de un aumento de 50% a 53%, que en el caso en que se trata de un aumento entre 90% y 93%.
Antes de aplicar esta transformación a las ecuaciones (5) y (6), debemos tomar en cuenta que en la mayoría de las aplicaciones prácticas las proporciones P no son directamente observables, lo que sí podemos medir son las frecuencias relativas h, por lo tanto, el modelo (5) lo podemos escribir como:

y en el (6):

Para aplicar los procedimientos tradicionales de estimación, debe cumplirse que la esperanza del término de error (log. h/1-h — log P/1-P), debe ser igual a cero, su varianza debe ser constante y los errores no deben estar autocorrelacionados.
Siguiendo el argumento de Theil13 en que se supone que las observaciones de cada celda han sido obtenidas independientemente y que el número de observaciones por casilla sea lo suficientemente grande, se puede demostrar que la esperanza del término de error será cero. La ausencia de correlación entre los residuos está garantizada por haber considerado muestras independientes. Sin embargo, hay dificultades con el supuesto de varianza constante (homocedasticidad).
Bajo el supuesto que las casillas se han conformado por una serie de muestras aleatorias de distintos tamaños en que se cumple la condición de independencia estadística14 y la característica de dicotomía, podemos considerar que las observaciones en cada una de ellas han sido generadas por un modelo probabilístico binomial. La teoría de las distribuciones de probabilidades nos dice que en este modelo la varianza de la proporción es igual a:
Esta expresión nos permite establecer la varianza de la proporción muestral en cada celda y como en general, tanto los P como los tamaños de muestras por casilla (n) serán distintos, entonces las varianzas de las proporciones para cada casilla serán necesariamente diferentes. Sobre la base de este resultado se puede demostrar que si el número de observaciones por casilla es suficientemente grande la varianza del término de error de los modelos (7) y (8) es aproximadamente igual a: 1 /nh (1 — h), en que tanto n como h se refieren a una sola casilla.15
Al romperse el supuesto de varianza constante (o equivalentemente si el modelo es heterocedástico) el método más eficiente de estimación es el mínimo cuadrático ponderado.16 La idea básica en este procedimiento de ajuste, es la de otorgar menos importancia a las observaciones con mayor varianza y más importancia a aquellas con varianzas menores. La aplicación de este principio lleva al resultado de que las varianzas serán todas iguales.
Si para realizar el ajuste multiplicamos cada igualdad de las que componen los sistemas de ecuaciones representados por (7) y (8) por 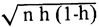
Dado el carácter de este trabajo sólo hemos bosquejado el problema y su solución debido a que es parte del conocimiento básico de aquellas personas especializadas en este tipo de temas. Los no iniciados deben recurrir a un buen programa de computación.
5. Consideraciones técnicas adicionales
El análisis de una tabla de contingencia a través del método de regresión presenta una serie apreciable de ventajas que derivan básicamente de un conjuntó de conceptos que le dan su riqueza analítica. Dentro de esos conceptos, en este apartado, pondremos especial interés en el coeficiente de determinación y en la prueba χ2.
Es sabido que en análisis de asociación existen una serie de coeficientes que intentan capturar la fuerza de la relación entre dos o más variables. El problema se presenta en el momento en que todos ellos entregan valores distintos llegándose en algunos casos extremos a diferencias sustanciales. Las personas que han trabajado sobre el tema parecen haber llegado al acuerdo de que los valores numéricos son distintos porque los coeficientes miden “cosas” diferentés.17
Al aplicar el análisis de regresión obtenemos el coeficiente de determinación (R2) como subproducto de la estimación de parámetros. Conceptualmente esta medida se interpreta como la proporción de la varianza total que es explicada por el modelo. En consecuencia el valor que alcance el coeficiente de determinación será una función de la forma de la relación y del tipo de variables que se usan para realizar el ajuste. También puede ser interpretado como el grado de ajuste que se ha alcanzado entre los valores predichos por el modelo y los valores observados.
Definamos R2 como:

en que e simboliza a la discrepancia entre los valores observados y los pronosticados por el modelo.
Si simbolizamos la frecuencia estimada por h, y operamos algebraicamente sobre la ecuación (7):

despejando ĥ se llega a: α2Ύ1X6 + α2X7 −1)−1}

Como e = h — h, en que h representa a las frecuencias relativas observadas, disponemos de todos los elementos necesarios para calcular R2. Operando de la misma forma sobre la ecuación (8) se llega a:
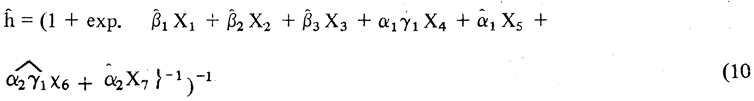
Los modelos que hemos considerado no toman en cuenta el número de observaciones por casilla (en el ejemplo hemos reemplazado el total de observaciones por 12. Por lo tanto, el término de error estimado e (discrepancia entre valores observados y estimados), nos da sólo una indicación respecto al grado de ajuste de nuestro modelo respecto a las proporciones en cada celda, pero no toma en cuenta el número de observaciones que hay en cada una de ellas.
Se puede derivar un test χ2 que sea sensible al número de observaciones por casilla. Para ello partamos de uno de los teoremas básicos de la estadística matemática que establece que si el tamaño de muestra es lo suficientemente grande entonces la distribución binomial tiende a la normal.18
Por otra parte, χ2 se define como una suma de variables aleatorias normales independientes elevadas al cuadrado, donde los grados de libertad igualan al número de sumandos.19
Como hemos supuesto que al interior de cada casilla de nuestra tabla, se cumplen las condiciones necesarias para aplicar la distribución binomial entonces para cada una de ellas la expresión:
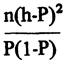
seguirá una distribución χ2, con un grado de libertad. Ahora bien, como a la vez hemos supuesto que las muestras se han obtenido independientemente, entonces las distinas χ2 serán estadísticamente independientes y como en nuestro ejemplo tenemos doce casillas, entonces tendremos que la suma:

o bien,

sigue una distribución χ2, con doce grados de libertad.
Podríamos someter a prueba la consistencia entre las frecuencias relativas observadas h y las proporciones teóricas P, pero como éstas no las conocemos y sólo disponemos de estimaciones (obtenidas por las ecuaciones del tipo (9) y (10)) podemos reemplazar los P por los ĥ. Sin embargo, hay que corregir el cálculo de grados de libertad, por cuanto hay un teorema que nos dice que debemos restar un grado de libertad por cada parámetro de χ2 que hayamos estimado.20 En el caso del modelo (7) hemos estimado 6 parámetros, por lo tanto, tenemos 6 grados de libertad. En el caso del modelo (8) hemos estimado 7 parámetros, lo que origina 5 grados de libertad. En todos los demás aspectos ésta es una prueba χ2 tradicional, donde la región crítica se encuentra ubicada en la cola derecha de la distribución.
6. Estimación de modelos mixtos
En las secciones anteriores hemos centrado nuestro interés sobre las potencialidades que se derivan de la formalización y hemos puesto especial énfasis en la consideracióñ de expresiones matemáticas que permitan incorporar factores explicativos de naturaleza cualitativa. Los problemas de estimación han jugado un papel secundario. Pero de aquí en adelante cambiaremos el eje de nuestra preocupación por lo que acentuaremos el tratamiento de las dificultades que surgen de la estimación de modelos cualitativos. Pero sólo tomaremos en cuenta aquellos problemas que sobrepasen los límites establecidos por el método mínimo cuadrático. Ello no quiere decir que nos olvidemos de la formalization sino que debe entenderse en el sentido de un cambio de énfasis. Aún más, introduciremos en esta sección, un tipo de discurso teórico que genera una nueva clase de ecuaciones de regresión. Hasta ahora hemos considerado sólo modelos en que todas y cada una de las variables explicativas son cualitativas, es decir, nos hemos preocupado por modelos absolutamente cualitativos. Ahora nos introduciremos en las peculiaridades que presenta la estimación de modelos que combinan variables cualitativas y cuantitativas. Podemos tomar como ejemplo un modelo en que la variable a explicar sea el número de hijos por familia y entre las explicativas aparezcan variables cualitativas como son las categorías ocupacionales y ciudades, y entre las cuantitativas, la edad actual de la mujer, edad al casarse, socialización etc.
Si las variables definidas se han construido sobre la base de observaciones individuales se nos plantean dos alternativas de análisis.
Por una parte, podemos cruzar las variables cualitativas de manera de definir un conjunto de subpobíaciones o submuestras y realizar un análisis de regresión entre las variables cuantitativas al interior de cada una de ellas.
La otra posibilidad consiste en la incorporación de las variables cualitativas al interior del modelo, para hacerlo se recurre a la definición de variables mudas. Una vez que establecemos estas variables, se pueden usar ios procedimientos de estimación ordinarios por lo que estaremos en condiciones de calcular todas las medidas estadísticas asociadas al modelo de regresión.
La diferencia esencial que existe entre ambos tipos de modelos es que el segundo nos permite medir directamente el impacto que tienen las variables cualitativas sobre la variable explicada.
Desde el punto de vista gráfico el primer tipo de modelos consiste en el ajuste independiente de un conjunto de hiperplanos de regresión. Uno para cada casilla definida por el cruce de las variables cualitativas. En cambio, el segundo es más restrictivo en la medida que considera un ajuste relacionado de los mismos. La asociación está dada por el hecho de que los distintos hiperplanos poseen las mismas inclinaciones y se diferencian por sus niveles, son estos últimos los que recogen los impactos de las variables mudas.
Por lo tanto, el modelo absolutamente cuantitativo (en la medida que sólo incorpora dicho tipo de variables en calidad de factores explicativos) se puede caracterizar por el hecho de que los coeficientes de regresión variarán de subpoblación a subpoblación. El modelo mixto impone la restricción de que los impactos de las variables métricas son los mismos para todas y cada una de la subpoblaciones y que el efecto de las variables cualitativas sólo modifica el término libre.
Ya hemos dicho que el modelo que orienta la exposición de esta sección ha sido ca lificado como mixto por cuanto las variables explicativas son tanto de naturaleza cualitativa como cuantitativa. La variable a explicar es el número de hijos por familia, las variables explicativas cualitativas son las categorías ocupacional del jefe de familia y algunas de las principales ciudades latinoamericanas. Las cuantitativas son: edad actual de la mujer, edad de la mujer al casarse, socialización urbana de la pareja, feminismo, religiosidad, tipo de matrimonio y participación ocupacional de la mujer.
El análisis se desarrolla al nivel de observaciones individuales, las cuales se disponen en una tabla de doble entrada construida sobre la base de las variables cualitativas. Al interior de cada una de las casillas tenemos un conjunto de observaciones individuales referidas a la variable a ser explicada (número de hijos por familia) y a las variables explicativas métricas. El número de observaciones por casillas (nij) es igual al tamaño de cada una de las submuestras.
En el modelo teórico de descomposición de la variable explicada las variables cuantitativas se han denotado por Z. Es así como Z1 define la edad actual de la mujer, Z2 la edad de la mujer al casarse y así sucesivamente hasta llegar a Z7; participación ocupacional de la mujer.
El modelo escrito de manera explícita es:

En que X1, X2..., X9 denotan las variables mudas que se construyen con el propósito de incorporar en la explicación el papel que teóricamente jugarán las ciudades y los grupos laborales.
En la tabla de descomposición teórica (esperada) sepuede ver que a mide el número esperado de hijos para los obreros no especializados residentes en Guayaquil. Los coeficientes gammas se refieren al efecto de “ciudades” tomando como base de comparación Guayaquil. De este modo γ2 representa el impacto que tiene sobre el número de hijos el hecho de que jefe de familia resida en Quito en lugar de Guayaquil y así sucesivamente hasta llegar a γ10 que muestra el efecto que tiene sobre la variable explicada el hecho de residir en Buenos Aires en comparación con Guayaquil.
Los coeficientes beltas expresan el impacto sobre el número de hijos de la categoría ócupacional tomando como basé de comparación fija la categoría de obreros no especializados. Por ejemplo, el coeficiente βr, captura el efecto relativo que tiene sobre el número de hijos el hecho de que el jefe de familia sea empleado en vez de obrero no especializado.
Los coeficientes delta representan el impacto lineal que tienen las variables métricas sobre el número de hijos. Esta interpretación es válida para todos los deltas a excepción de δ1 y δ2 por cuanto el efecto de la variable edad de la mujer(Z1)es no lineal. El impacto de Z1 sobre Y manteniendo constantes todos los otros regresores es:

es decir, su efecto depende del nivel de Z1 y de los dos parámetros deltas, en que δ1 muestra la parte constante de la variación y δ2 la mitad de la tasa de cambio-delmismo (aceleración). La variación de la tasa de cambio es constante e igual a 2δ2, como se puede apreciar por medio de:



Una vez descrito el modelo debemos preocuparnos por su estimación. Con este objeto escribamos el modelo (11) de manera compacta haciendo uso de matrices:

W es una matriz de orden nxk y de rango completo, en cuyas columnas podemos distinguir los regresores del tipo X y los del tipo Z. n es el número de observaciones y k es en número de parámetros.
Y y e son vectores columnas de orden nxl, y B es el vector columna que contiene los parámetros y su orden es kxl.
Si a este modelo le agregamos los supuestos tradicionales respecto al término de error:

completamos su especificación teórica.
A pesar de que en este momento estamos en condiciones de proceder al ajuste, puede resultar de cierto interés plantear el mismo modelo desde otro ángulo.
Si a la matriz W la particionamos distinguiendo las variables mudas y las cuantitativas y realizamos la misma operación sobre el vector de parámetros en que distinguimos, de una parte, los coeficientes betas y gammas y de otra los deltas, tendremos:

Realizando la operación del producto matricial indicada concluimos que el sistema de ecuaciones representado por (13) se transforma en:

Sabemos que la aplicación del criterio mínimo cuadrático a la ecuación (13) entrega por resultado:

Realizando operaciones convenientes sobre (15):

Una vez que se invierte la matriz particionada y después de un tedioso pero no difícil proceso de manipulación algebraica obtenemos fórmulas que nos permiten estimar por separado los coeficientes de regresión asociados a las variables mudas y a los regresores métricos:

en que M y N se definen como:

Es evidente que en el ajuste del modelo expuesto en esta sección pueden aparecer algunos problemas econométricos que dificultan el proceso de estimación, por ello en la octava sección haremos una breve discusión de aquellos que a nuestro juicio tienen una mayor probabilidad de surgir en investigaciones que envían sobre este tipo de ecuaciones así como también aparecen en las que expondremos a continuación.
7. Estimación de ecuaciones de regresión individuales a partir de datos agregados
Trataremos este problema de estimación como punto de partida aun cuando no tenga relación directa con los modelos que hemos presentado en las secciones anteriores. Sin embargo, nos permite relevar y entregar una solución fácil al tipo de problemas que debemos enfrentar posteriormente.
Supongamos que nos interesa ajustar un modelo lineal en que todas y cada una de las variables se han construido á partir de observaciones individuales. En términos generales podemos representar la relación entre el conjunto de observaciones y regreso-res por medio de:

donde X es una matriz de orden (nxk) y de rango k (n es el número de observaciones y k es el número de parámetros a estimar) y k es menor o igual que n. Y y e son vectores columna de orden (nxl) y B es un vector de orden (kxl).
Además se agregan los supuestos tradicionales relativos al término de error, vale decir:
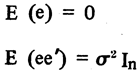
Ahora bien, supongamos que en lugar de disponer deja información original sólo contamos con las medias de X, e Y simbolizadas por X̄, Ȳ. Si hemos formado m grupos (k > m > n) podemos establecer el modelo:

Con los datos que disponemos no tendremos dificultades para realizar el ajuste del modelo (18) ni en estimar sus correspondientes coeficientes de regresión. Si embargo, el vector así estimado no guarda una conexión tan directa como parece a primera vista coa B de la ecuación (17). Para establecer algún gradó de correspondencia entre ambos vectores paramétricos y analizár los problemas de estimación que aquejan a la ecuación (18) es necesario que estudiemos el procedimiento por medio dd cual a partir de (17) se llega a (18).
Para ello definamos una matriz de agrupamiento P de orden (mxn) cuya característica es que cada línea se refiere a un grupo y los elementos de ellas son tanto las frecuencias relativas al interior de cada grupo cuanto ceros. Las primeras aparecen cuando las observaciones se encuentran incluidas en el grupo y los ceros cuando la observación no corresponde al grupo a que se refiere la iínpa. Tomemos como ejemplo la tercera linea de P, es decir el tercer grupo. Si este agregado está formado por ties observaciones: la cuarta, séptima y n-ésima, entonces el tercero, séptimo y n-ésimo elementos de la tercera línea de P serán iguales a un tercio y todos los restantes serán iguales a cero.
Dada la matriz P estamos en condiciones de establecer las siguientes relaciones entre las variables individuales y agrupadas:

Dadas estas ecuaciones podemos reexaminar los supuestos relativos al vector estocástico de error.21

Resulta claro que no se introducen modificaciones en torno al primer supuesto, sin embargo, la matriz de varianzas y covarianzas de los errores se ha modificado. Dada la naturaleza de la matriz P el producto matricial PP’ da origen a una matriz diagonal de orden mxm. Como, en general, estos términos serán distintos entre sí se concluye que la transformación lineal operada sobre las variables individuales ha generado un problema de heterocedasticidad el cual afecta a la propiedad de varianza mínima. En consecuencia, el método de estimación mínimo cuadrático ordinario ya no gozará de una de las propiedades que lo han hecho tan popular lo que ha llevado a que bajo estas circunstancias se prefiera utilizar los estimados mínimos cuadráticos generalizados, también conocidos bajo el nombre de estimadores de Aitken.22
Al aplicar este método de estimación, las expresiones correspondientes al vector de estimadores (b) y a la matriz de varianzas y covarianzas {var (b)} son:

Por lo tanto si deseamos estimar la relación que existe entre un conjunto de variables individuales y sólo contamos con información grupal debemos tomar en cuenta que el agrupamiento destruye la propiedad de homocedasticidad que se ha supuesto al nivel individual. Debido a ello el procedimiento de estimación más adecuado es el mínimo cuadrático generalizado.
Antes de abandonar está sección debemos realizar algunas acotaciones adicionales.
i) En la definición de la matriz de regresores X no se impone ninguna restricción sobre el tipo de variables, por lo tanto, puede estar compuesta tanto por variables métricas como por variables mudas de modo que las conclusiones obtenidas son de carácter general.
ii) Al aplicar el procedimiento de estimación recomendado, se genera un problema de predicción cuya solución se debe a A. Goldberger.23 Este autor demuestra que el mejor predictor lineal e insesgado (mejor en el sentido varianza mínima) en aquellos casos en que se ha usado el procedimiento de Aitken es:

donde X0 es un vector línea que contiene los regresores de predicción. W, es un vector columna definido por:

en que e0 es el residuo estocástico correspondiente al vector de predicción X0. El vector columna e es el que contiene los errores correspondientes a la aplicación del método de estimación mínimo-cuadrático generalizado.
8. Estimación de un modelo agregativo y cualitativo
Supongamos que nos interesa estimar efectos de variables cualitativas sobre variables cuantitativas agregadas. Nuestro problema se centra en la estimación de un modelo de regresión en que para explicar el número medio de hijos utilizamos como variables explicativas categorías ocupacionales y ciudades importantes de algunos países latinoamericanos.
Ahora bien, por medio del cruce de las variables cualitativas podemos construir la tabla de la página siguiente, en cuyo interior tenemos la descomposición teórica del número medio de hijos por familia.
Todos los coeficientes de esta tabla exceptuando α, miden impactos relativos, en que por construcción del modelo las categorías tienen efectos independientes, es decir, no se consideran interacciones. Sabemos por lo dicho en la tercera sección que esto no constituye una limitación inherente al uso de variables mudas. Sólo significa que no las hemos considerado en este modelo. La descomposición teórica que hemos presentado en la tabla nos permite asignar las siguientes definiciones a los parámetros: α representa el número medio esperado de hijos de las familias cuya cabeza es obrero no especializado y residente de Guayaquil.
β1 puede interpretarse como el impacto que tiene sobre la variable explicada el hecho de que el jefe de familia sea obrero especializado en lugar de no especializado.
β2 mide el efecto de ser empleado en lugar de obrero especializado.
β3 indica el impacto que tiene sobre el número medio de hijos el hecho de que el jefe de familia sea directivo en lugar de empleado.
Los coeficientes γ se refieren a los efectos relativos de ciudades. De este modo, γ1 γ2 γ3 reflejan los impactos de residir en Caracas en lugar de Guayaquil; en Río de Janeiro en vez de Caracas y en Buenos Aires en lugar de hacerlo en Río de Janeiro respectivamente.
Nótese que en este caso hemos definido los parámetros en términos de efectos relativos con base variable (siempre se compara con la casilla vecina) en lugar de utilizar una base fija tal como lo habíamos hecho hasta ahora.
Una vez planteada la descomposición teórica del número medio de hijos debemos proceder a la asignación de un conjunto de variables mudas o regresores que nos permita movernos a través de las distintas casillas de la tabla Los regresores definidos son los siguientes:
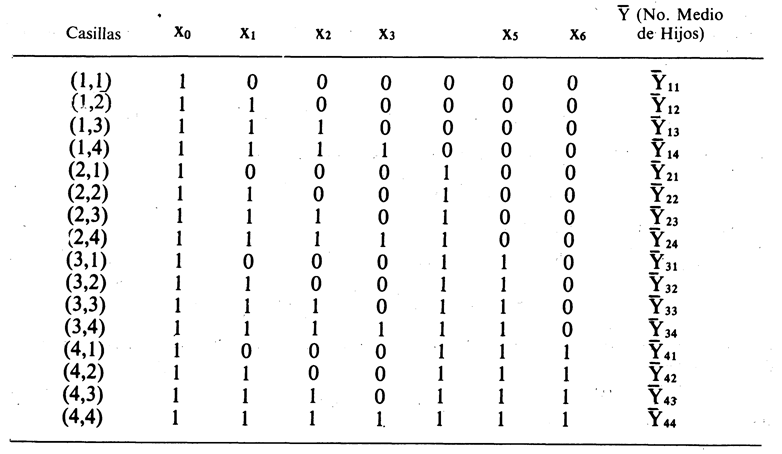
El mejor procedimiento de estimación del modelo:

es el mínimo cuadrático generalizado por cuanto debemos tomar en cuenta que las varianzas de las medias muéstrales para cada una de las casillas serán en general distintas, por consiguiente no podemos mantener el supuesto de homocedasticidad.24
Las varianzas estimadas de la variable a explicar están dadas por la fórmula:

en que 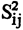
Estas varianzas estimadas se pueden disponer en una matriz diagonal:

En este caso las fórmulas del vector de estimadores y de la matriz de varianza y covarianza son:

Los elementos de la diagonal principal de la matriz de varianza y covarianza son los cuadrados de los errores estándares de los estimadores. De este modo, la raíz cuadrada del primer término de la diagonal de V entrega el error estandard de α^, del segundo el de β^1 y del séptimo el de γ^3.
Los elementos de la matriz de varianza y covarianza se determinan sobre la base de las fórmulas correspondientes a la varianza de la variable explicada. Así, si la variable que pretendemos explicar son proporciones en lugar de medias aritméticas debemos utilizar:

Por otra parte, debemos agregar que en aquellos casos en que la variable explicada tiene limitaciones en su recorrido es recomendable someterla a transformaciones matemáticas. En el apartado 4.3 hemos examinado con algún detenimiento la transformación logit aplicada sobre la variable a explicar y hemos bosquejado los problemas de estimación que se desprenden de ella por lo que no insistiremos sobre este punto.
En resumen, el procedimiento que hemos utilizado en esta sección se puede describir en los siguientes términos:
1) Disponemos de un cuadro que contiene 16 observaciones. Siguiendo una de las normas básicas del trabajo estadístico, planteamos un modelo de análisis que permita describir de manera resumida los tipos de conexiones entre las variables, originándose de este modo, un conjunto sintético de medidas. Estos son esencialmente los coeficientes de regresión los cuales nos permiten discernir conceptualmente los efectos de las variables cualitativas.
2) Al establecer un modelo en los términos planteados, se generan algunos problemas de estimación debido a que se rompe el supuesto de homocedasticidad. Por ello recurrimos al procedimiento de estimación mínimo cuadrático generalizado.
3) Si bien el modelo que hemos desarrollado no impone, desde el punto de vista teórico, ninguna restricción en el recorrido de la variable explicada, no existen mayores dificultades al considerar variables con recorrido limitado. Para ello es recomendable someter previamente dichas variables a alguna transformación matemática.
9. Algunos problemas de estimación usuales en modelos de regresión con variables mudas
En esta sección recopilamos una serie de problemas susceptibles de presentarse en la estimación de modelos cualitativos o mixtos ya sea que para ello se cuente con información agregada o desagregada.
Además de plantear la denominada “trampa de las variables mudas”, dedicamos espacio a las formas específicas que pueden asumir la multicolinealidad y la heterocedasticidad. Agregamos a ello, las implicaciones que se derivan de la presencia de dichos problemas de manera que el investigador tenga medios que le permitan reconocerlos y detectarlos así como también mostramos algunos caminos para su solución.
Por último, nos preocuparemos por mostrar la manera adecuada de proceder al cálculo del coeficiente de determinación.
9.1. La trampa de las variables mudas
En los modelos que incluyen variables mudas no hemos considerado explícitamente un término libre. Por ejemplo, en la ecuación (11) se puede apreciar que todos y cada uno de los parámetros se encuentran afectados por una variable X. Si hubiésemos incluido explícitamente el coeficiente de posición se generaría un problema de multicolinealidad perfecta. En efecto, agregar una constante implica adicionar un regresor (por ejemplo X1) que siempre asume el valor unitario. Como el regresor X1 siempre será igual a 1 en la matriz de regresores aparecerán dos columnas idénticas y, por lo tanto, no se podrá calcular la inversa de XX.
Si bien este problema se presenta con mucha claridad al plantear el modelo teórico y es susceptible de ser eliminado con facilidad, desde el punto de vista computacional pueden surgir algunas complicaciones que nos obligan a estar alertas.
En algunos programas de computación no existe la opción de incluir o no un término libre sino que lo asigna automáticamente a cualquier modelo. Por lo tanto, si disponemos de un programa que incorpora una columna de valores unitarios en la matriz de observaciones X, y el usuario alimenta a la máquina con todos los valores de los regresores —incluido X1 que se caracteriza por asumir sólo el valor unitario—, entonces habrá dificultades en la estimación. En efecto, el programa es de naturaleza tal, que a la matriz de observaciones que contiene a los k regresores le agrega una columna de unos, lo que conduce a que por una parte, dispongamos de las estimaciones correspondientes a k + 1 parámetros —en circunstancias que sólo se han definido teóricamente k de ellos— y, por otra, se materialice un problema de rango en la matriz de observaciones. Esta dificultad genera un problema de estimación que se conoce con el nombre de colinealidad, o de multicolinealidad.
Ahora bien, si el modelo a ser ajustado sólo incorpora regresores mudos, el problema se detecta fácilmente a posteriori. El computador no entregará resultados y nos alertará respecto a la singularidad de la matriz de observaciones.
Sin embargo, si el modelo es tal que combina variables mudas con variables métricas, suele suceder que a pesar de haberse cometido el error señalado podemos obtener resultados de todas las medidas que nos interesan: estimaciones de coeficientes de regresión, R2, errores estándares de los parámetros, etc. Esto se debe a que en el cálculo de la matriz inversa se recurre a una serie de aproximaciones de manera tal que se obtienen resultados a pesar de la singularidad. Pero, si se pide el cálculo del producto (X’X) (X’X’)-1 acontece que el resultado dista bastante de la matriz identidad.
Si el investigador no es cuidadoso en el control de la información que ingresa al computador puede no darse cuenta de que algo anda mal. El peligro es aún mayor en aquellos casos en que se toman los resultados y se comienza el análisis sin detenerse previamente en la consideración de los problemas econométricos fundamentales que suelen aquejar al modelo de regresión.
A modo de resumen, podemos afirmar que si pretendemos estimar ecuaciones del tipo de la relación (11) y el programa de computación produce automáticamente el coeficiente de posición el listado de variables debe excluir los regresores del tipo de X1.
En todo caso, siempre es conveniente investigar respecto a multicolinealidad, considerando los frecuentes errores de entrada de datos y la colinealidad real que puede existir entre las variables explicativas métricas.
9.2. Algunas consideraciones sobre multicolinealidad
En el tipo de modelos que estamos tratando, este problema puede surgir desde varías fuentes.
Tal como se ha visto en la segunda sección en los modelos cualitativos se puede generar a raíz de una mala asignación de valores a las variables mudas o como se ha consignado en 9.1, puede ser inducido por programas de computación que agregan una constante a la ecuación. En los modelos mixtos además de estas dos fuentes hay que reconocer que su génesis puede radicar en la relación lineal estrecha que exista entre algunos de los regresores métricos.
En todo caso, lo que importa en una primera aproximación es reconocer la existencia del problema. Cuando hay multicolinealidad perfecta la matriz que se debe invertir para obtener los estimadores de los parámetros y la matriz de varianza y covarianza es de rango incompleto. Esto, significa que la inversa no existe y, por lo tanto, no es posible obtener las estimaciones.
Este caso se relativiza bastante en la medida en que la multicolinealidad no es perfecta. Cuando ello ocurre es posible obtener los valores de los estimadores de los parámetros, sus varianzas, calcular el coeficiente de determinación, etc. Pero, debido a la relación lineal estrecha, las varianzas de los estimadores resultan ser exageradamente grandes. Generalmente, los resultados son hasta cierto punto contradictorios ya que por una parte, tenemos coeficientes de regresión estimados no significativos; y de otra, suele aparecer un coeficiente de determinación elevado.
La solución econométrica a este problema radica en acopiar información externa al modelo que permita establecer una relación de proporcionalidad entre los parámetros que están asociados a las variables colineales. Si dicha relación es conocida por medio de simples sustituciones algebraicas se pueden evitar las dificultades.
Además, consignamos que la solución de uso cotidiano en la investigación empírica radica en la eliminación de una de las variables colineales. Esta forma de abordar el problema no es recomendable en la medida que se presentan dificultades en la asignación de contenido a los parámetros.25
En secciones anteriores hemos visto que este problema se genera esencialmente en la agregación.
Además, hemos argumentado que en aquellas situaciones en que no se puede sustentar el supuesto de homocedasticidad el método de estimación más eficiente es el mínimo cuadrático generalizado. Si aplicamos los mínimos cuadráticos ordinarios las varianzas de los estimadores resultarán ser mayores. Por lo tanto, el procedimiento de estimación de uso corriente será más impreciso que el mínimo cuadrático generalizado.
El procedimiento de Aitken se basa en el principio de dar menos ponderación a aquellas observaciones que tienen mayor dispersión que a las que tienen menor. Se “eree” menos a aquellas observaciones que generan mayores errores observados que a las que generan menores errores.
Otra fuente que origina heterocedasticidad es la relación que en ocasiones se puede observar entre los residuos y las variables explicativas. En aquellos casos en que existe este tipo de vínculos no sólo se generan problemas de sesgo en los estimadores sino también de consistencia.26
La solución corriente a este problema se encuentra en el uso del método mínimo cuadrático generalizado a pesar de que surgen algunas dificultades en la determinación de los elementos de la matriz de varianza y covarianza.
Si por ejemplo, hemos establecido una relación proporcional entre un regresor y el término de error:

podemos reemplazar los elementos de la matriz diagonal V:
y posteriormente proceder a aplicar el método general. La dificultad estriba en llegar a establecer la forma de la relación entre los errores y uno, o una combinación lineal de regresores.
En todo caso antes de intentar una solución a un problema, es necesario tener elementos para detectarlo. En esta línea hay dos tipos de pruebas de hipótesis que prestan utilidad.
Se puede recurrir a la prueba de Goldfield y Quandt,27 la cual sólo presenta utilidad práctica para aquellos casos en que tenemos un reducido número de datos (los programas de regresión disponibles presentan restricciones).
Pero cuando la cantidad de observaciones es elevada resulta más conveniente recurrir a la prueba de igualdad de varias varianzas. Esta prueba se realiza con la F de Snedecor y presenta la dificultad de que sus resultados dependen de los grupos que se formen para calcular las varianzas. Sin embargo, en nuestros modelos mixtos supuestamente no tenemos tal dificultad por cuanto los agrupamientos realizados tienen plena validez teórica.
En resumen, el problema de heterocedasticudad se encuentra controlado en el caso de los modelos cualitativos agregados. En los modelos mixtos hay que investigar respecto a la dependencia de la varianza de los errores respecto a las variables métricas. Para ello lo más conveniente es aplicar la prueba F. Una vez detectado el problema debe investigarse la naturaleza de la relación. Una vez que la conocemos definimos la matriz V y, por último, aplicamos el método mínimo cuadrático generalizado.
9.4. El coeficiente de determinación
Si consideramos que la selección de formas funcionales alternativas envuelven un compromiso entre varios criterios, incluyendo los sustantivos y los de simpleza de la función, es posible argumentar que a menor número de parámetros mayor simpleza. Es convencional recoger esta idea y comparar coeficientes de determinaciones corregidos mediante la fórmula:

Este coeficiente penaliza a aquellas funciones que tienen un gran número de parámetros (k).
Por lo tanto, si debemos comparar el grado de bondad de ajuste de modelos alternativos y con distinto número de regresores se hace necesario entregar tanto el coefir dente de determinación ordinario como el corregido.
10. Conclusiones
Las dos primeras secciones de carácter sustantivo nos han permitido mostrar una equivalencia analítica entre el análisis de varianza y el análisis de regresión con variables mudas. Este resultado es ampliamente conocido en la literatura técnica.28
A continuación, nos hemos preocupado por las complejidades que surgen en el proceso de estimación si la variable explicada es una proporción o un porcentaje. Para el tratamiento de las denominadas tablas de contingencia o tablas de entradas múltiples se han desarrollado una serie de instrumentos de análisis que cubren desde el análisis de asociación hasta el análisis de variables múltiples a la Lazarsfeld. Tal vez la limitación más importante de dichas técnicas radica en la imposibilidad de medir el efecto que tiene cada categoría sobre la variable explicada. Como hemos visto a lo largo de este trabajo, la ventaja fundamental del análisis de regresión con variables mudas radica en la descomposición de la variable explicada en un conjunto de impactos o efectos, asociados a las categorías de las variables explicativas. Además, estos efectos pueden ser independientes o interactivos.
Al realizar un análisis de regresión sobre una tabla de contingencia, podemos calcular no sólo los impactos de cada una de las categorías o de cada uno de los regresores, sino también intervalos de confianza, intervalos de predicción, etc.
Además, obtenemos una medida para la fuerza de la relación: el coeficiente de determinación R2. Este coeficiente se interpreta como el porcentaje de la varianza total que explica el modelo. En general, se abren las puertas para hacer uso de todos los conceptos elaborados en torno al poderoso modelo de regresión.
La diferencia básica entre el modelo de regresión tradicional y el que usa variables mudas, radica en que en la mayoría de los casos el primero, permite estimar efectos de variables, en tanto que el segundo sólo permite estimar efectos de regresores. En todos los desarrollos que hemos presentado se han establecido reglas de correspondencia entre regresores y categorías. A pesar de ello, podemos investigar la significación del efecto de una variable.
Supongamos que, al aplicar el modelo (5) nos preguntamos acerca de la significación de la variable ingreso. Se puede levantar una respuesta estableciendo la hipótesis nula:

en contra de la alternativa:

La respuesta que se entregue dependerá del resultado de la prueba de hipótesis.
Sabemos que una de las limitaciones fundamentales en el análisis de tablas de contingencias viene dada por el número de observaciones. El número de casillas aumenta en forma multiplicativa en relación al número de variables cruzadas y al número de categorías por variable. Esta restricción es común a todas las técnicas de análisis de contingencia y por lo tanto, es perfectamente aplicable al modelo de regresión con variables mudas. Pero hay una diferencia en cuanto a las consecuencias que acarrea la pérdida de grados de libertad en un análisis x2 y en uno de regresión. En el primero se agotan en las pruebas de hipótesis mientras que en el segundo repercute a través de todo el modelo.
Estas consideraciones tienen especial relevancia si recordamos que en el análisis de la cuarta sección, hemos reemplazado las n observaciories originales por un número igual al de casillas. Por lo tanto, hemos sufrido una pérdida importante de grados de libertad, la que se manifestará en todas las medidas que usualmente se calculan en torno al modelo de regresión.
Queremos destacar que aun cuando no hemos estudiado todas las posibilidades de descomposición de la variable explicada, hemos entregado una serie de principios que nos permiten expresarla como la suma de un conjunto de efectos y a partir de ellos construimos un modelo matemático. En realidad el procedimiento que hemos utilizado contiene los siguientes pasos:
1) Descomponga la variable explicada en una suma de efectos. Se supone que para ello se hace uso de la teoría.
2) Asocie a cada efecto o parámetro un regresor X.
3) Escriba el modelo. Es decir, plantee una ecuación que consista de parámetros y variables X.
4) Imponga valores numéricos a las distintas X, de manera que se pueda realizar una asociación entre el conjunto de valores de X y cada casilla de la tabla de contingencia.
5) Una vez definido el modelo y conocidos los valores de las variables proceda al ajuste. Si la variable a explicar es una proporción, recuerde que debe usar el criterio mínimo cuadrático ponderado y la conveniencia de la transformación de la variable.
6) Finalmente, proceda al análisis de resultados. Tenga en cuenta que sus resultados no son independientes de su teoría.
A partir de la séptima sección hemos cargado el énfasis de la exposición en favor de los problemas de estimación. En buenas cuentas lo único que hemos hecho ha sido aplicar sistemáticamente los principios que deberán orientar toda investigación en que el análisis de los datos se realiza a través del modelo de regresión:
i) Investigar hasta qué punto se cumple el conjunto de supuestos en que descansa el método de estimación mínimo cuadrático ordinario.
ii) Desarrollar las formas alternativas de detección de problemas de estimación, y
iii) Aplicar, en consecuencia, los mejores métodos de estimación disponibles.
La parte (i) de los principios, nos ha llevado a plantear los problemas de multicolinealidad y heterocedasticidad.
La multicolinealidad se introdujo a raíz de la “trampa de las variables mudas” y se dedicó algún espacio a su posible presencia en los modelos que sirven de referencia a este trabajo.
El tratamiento de heterocedasticidad se incorpora a raíz de la agregación de observaciones, así como a la posible relación funcional entre los residuos y los regresores.
La parte (ii) nos ha enviado sobre una breve discusión respecto a la forma más adecuada de someter a prueba la presencia de esos problemas. En cuanto a las fuentes de heterocedasticidad hemos planteado dos alternativas. Una que podemos calificar como esencialmente teórica que consiste en reconocer que si trabajamos con datos agregados es difícil sostener el supuesto de homocedasticidad, bajo la condición de haberlo aceptado para datos individuales. La otra, puede ser denominada cofno fuente empírica por cuanto descansa en la existencia de relación funcional entre la va-Tianza del error y a lo menos uno de los regresores. Cuando éste es el caso, hemos concluido que es posible aplicar la prueba tradicional de igualdad de varias varianzas.
La presencia de relación iineal entre los regresores, se detecta a través del examen de los errores estándares estimados, o bien, por medio de las correspondientes pruebas de hipótesis de los parámetros. El habitual examen de la matriz de intercorrelaciones, que normalmente se realiza con el propósito de detectar multicolinealidad, puede llevar a resultados engañosos: el hecho de que las correlaciones simples se distribuyan en el entorno del valor cero, no necesariamente implica ausencia de colinealidad. En efecto, a veces se desliza al interior del modelo a consecuencia de combinaciones lineales estrechas entre un conjunto de regresores.
Debido a la presencia de heterocedasticidad ha sido necesario incorporar el método de estimación mínimo cuadrático generalizado. En cada caso nos hemos preocupado por especificar la forma que asume la matriz de ponderaciones que ha sido simbolizada indistintamente por P o por V.
El símbolo P ha sido utilizado en el modelo que pretende estimar la relación entre variables individuales, pero la información disponible es la media de ios agregados. Los elementos de la matriz diagonal P están definidos por el peso relativo de cada observación en el grupo a que pertenece. Hemos utilizado el símbolo V cuando los elementos de la matriz de ponderaciones son varianzas.
Por último, hemos tratado una serie de tópicos de menor trascendencia. Hemos considerado una prueba ji-cuadrado que nos permite evaluar la bondad de la especificación del modelo, así como nos preocupamos por establecer la necesidad de encontrar el contenido sustantivo de los coeficientes de regresión asociados a las variables mudas. Esto último es de importancia fundamental por cuanto nos permite adscribir un sentido teórico a las pruebas de hipótesis aplicadas sobre los parámetros.
Notas al pie
N. del A.: Agradezco los comentarios y sugerencias realizados por Rosa María Rubalcava, que se han traducido en claridad de exposición y en rigor conceptual. Las imprecisiones q-ue aún subsistan así como las deficiencias que encuentre el lector son de responsabilidad exclusiva del autor.
1 Un ejemplo conspicuo se encuentra en el libro de Sydney Siegel, Nonparametric Statistics for the Behavioral Science, McGraw Hill, 1956.
2 En lugar del término variable dependiente usaremos los vocablos variable a explicar o explicada, y en lugar de variable independiente el de variable explicativa. Ello se debe, por una parte, a que si bien en las matemáticas es posible plantearse la existencia de una variable que se mueva independientemente, lo mismo difícilmente puede ser sostenido para las variables sociales. Y por otra parte, la diferencia terminológica también alude al hecho que el mpdelo trata de explicar un fenómeno (representado por una variable) sobre la base del comportamiento de otros fenómenos que son usados como explicativos del primero.
3 Con el único propósito de facilitar la redacción, usaremos como sinónimo las expresiones: volumen de producción industrial e industrialización.
4 En general un polinomio es una expresión matemática que contiene más de dos términos. En este texto nos referimos específicamente a igualdades del tipo:

Sabemos que dados dos puntos es único el polinomio de grado uno que pasa por ellos, dados tres puntos es único el polinomio de grado dos y que a través de (n + 1) puntos puede hacerse pasar un polinomio de grado n.
5 En particular, el término de error observado é, se usa como uno de los elementos del coeficiente de determinación R2.
6 El término regresor que se aplica normalmente a las variables del lado derecho de una ecuación de regresión permite llamar la atención sobre la posible no correspondencia entre aquellas y una variable sustantiva. Por ejemplo una variable tricotómica cualquiera (como sería el caso de las preferencias partidarias tricotomizadas en centro, derecha e izquierda) sólo puede ser incorporada dentro del modelo por dos o tres regresores, según las definiciones de variables mudas que se utilicen.
7 Los que se sistematizan en las conclusiones
8 Argüello, Omar: “Estructura agraria, participación y migraciones internas.” Migración y Desarrollo, No. 3, CLACSO, Buenos Aires, 1974.
9 Goldberg, Arthur, Econometric Theory, John Willey, New York 1964, págs. 222-224.
10 Goldberg, Arthur, op. cit., págs. 248-251.
11 Theil, Henry, Statistical Decomposition Analysis, North Holland, Amsterdam, 1972, págs. 166-173.
12 Nótese que las ecuaciones (7) y (8) se derivan directamente de las (5) y (6) sumando log 
13 Theil, op. cit., págs. 176-177.
14 Tanto en el interior de cada una de las casillas cuanto entre elias.
15 Ver Theil, op. cit., págs. 174-178.
16 Este método de estimación es equivalente al método mínimo cuadrático generalizado.
17 Ver, L. Goodman y W. Kruskall: Measures of Association for Cross Classification. Journal of the American Statistical Association. Vol. 49, No. 268, diciembre 1954, págs. 732-764. También, Hildebrand, David, et al., Analysis of Ordinal Data Sage publications Inc. California, 1977.
18 Estrictamente con n →∞ y P fijo ya que si n →∞ v P →0 entonces la distribución binomial tiende a la función de Poisson.
19 Ver, por ejemplo, John E. Freund, Mathematical Statistics. Prentice - Hall. Englewood. N.Y. 1962, cap. 8.
20 Hoel Paul. Introduction to Mathematical Statistics. John Wiley. New York, 1962. pág. 250.
21 Recuérdese que al especificar el modelo para las observaciones individuales hemos supuesto que: E(e) = 0 y E(ee’) =σ2In.
22 A. C. Aitken: On Least-Squares and linear combinations of observations. Pro. Royal. Soc., Vol. 55, págs. 42-48, 1934.
23 Referencia tomada de J. Johnston: Econometric Methods. John Wiley, New York, 1972. págs. 212-213.
24 En el modelo de regresión se cumple que la varianza del término de error es igual a la varianza de la variable explicada:
Sea,
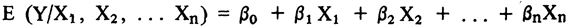
el valor esperado de Y dado el conjunto de regresóres X. Además, tenembs:

Restando la primera de la segunda ecuación:

El término de la izquierda es la varianza de la variable explicada y el de la derecha es la varianza del término de error ya que:

Por lo tanto: Var (Y) = Var(e)
25 Para evaluar las consecuencias de la eliminación de una variable explicativa en caso de relación lineal estrecha entre ios regresores, consideremos el modelo:

Ahora bien, partamos del supuesto que la teoría que origina esta ecuación nos señala que ambas son variables “relevantes” y que estamos interesados en evaluar el efecto de X1 sobre Y, manteniendo constante X2 (β1)y el impacto de X2 controlando X1 (β2). En el ajuste del modelo constatamos que existe una relación lineal estrecha entre los regresores:

la cual nos impide encontrar resultados estadísticamente signiñcativos. Supongamos que decidimos eliminar X1 del modelo original. Debido a que la eliminación no significa control tendremos problemas en asignar contenido sustantivo a los valores estimados de los parámetros:
Reemplazando la segunda ecuación en la primera:

Luego el coeficiente de X2 no mide el impacto de X2 manteniendo constante X1 sino que es una combinación lineal de ese efecto y el impacto de X1 (β1) a través de la relación entre X2 y X1 (β1 b). De forma similar se puede interpretar la estimación del término libre.
Nótese que si b = 0, el coeficiente estimado tiene el mismo sentido que en la relación original.
26 Wonnacott y Wonnacott, Econometrics. John Wiley, New York, 1970. págs. 149-155
27 Goldfield, S. M. y Quandt, R. E.: Some Tests For Homosedasticity, Journal of the American Statistical Association 60, págs. 539-547.
28 Ver, por ejemplo, Wonnacott and Wonnacott, Econometrics, op. cit., págs. 77-79.