[Paper] [Documentation]

The Python package of differential nearest neighbors regression (DNNR): Raising KNN-regression to levels of gradient boosting methods.

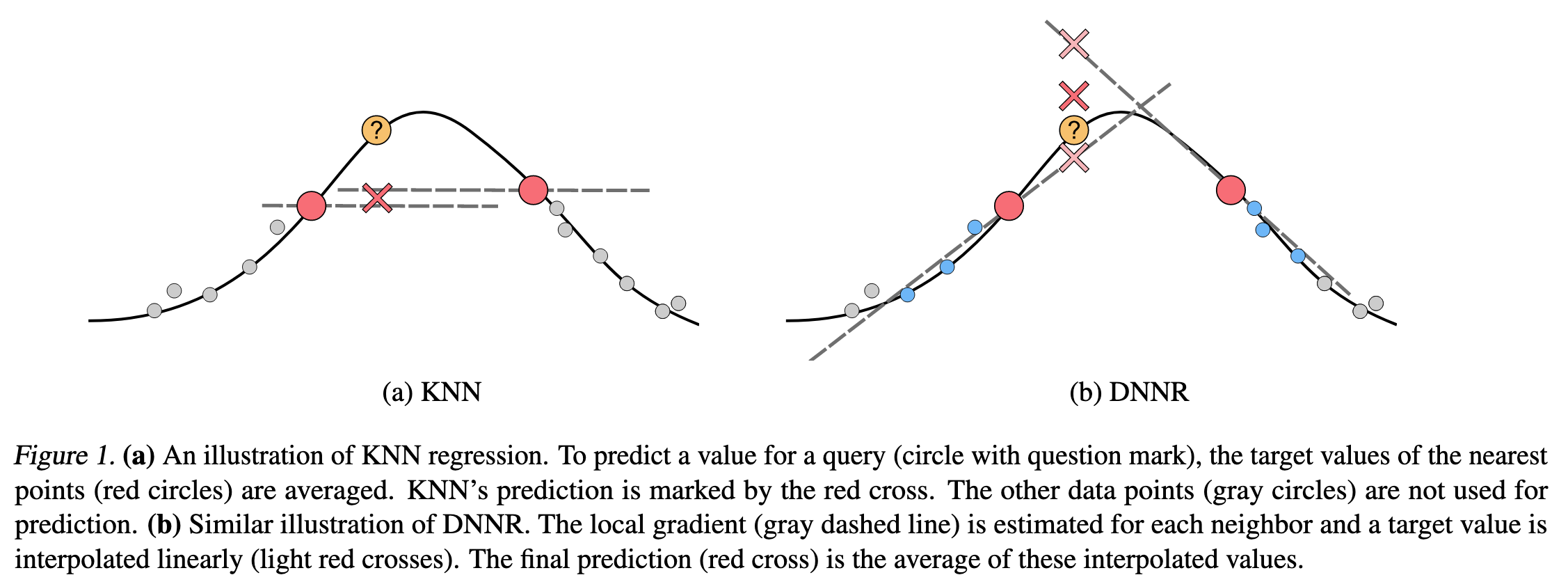
Whereas KNN regression only uses the averaged value, DNNR also uses the gradient or even higher-order derivatives:

Our implementation uses numpy, sklearn, and the annoy approximate nearest neighbor index. Using annoy is optional, as you can also use sklearn's KDTree as index. We support Python 3.7 to 3.10.

To install this project, run:

pip install dnnr

import numpy as np
from dnnr import DNNR

X = np.array([[0], [1], [2], [3]])
y = np.array([0, 0, 1, 1])

model = DNNR(n_neighbors=1, n_derivative_neighbors=3)
model.fit(X, y)
model.predict([[1.5]])
# Will output: 0.25

Also check out our Jupiter Notebook on how to use DNNR.

DNNR has three main hyperparameters:

• n_neighbors: number of nearest neighbors to use. The default value of 3 is usually a good choice.
• n_derivative_neighbors: number of neighbors used in approximating the derivatives. As a default value, we choose 3 * dim, where dim is the input dimension.
• order: Taylor approximation order, one of 1, 2, 2diag, 3diag. The preferable option here is 1. Sometimes 2diag can deliver small improvements. 2 and 3diag are implemented but usually do not yield significant improvements.

We recommend a hyperparameter search over the n_derivative_neighbors variable to archive the best performance.

For all options, see the documentation of the DNNR class.

python3 -m venv venv      # create a virtual environment
source venv/bin/activate  # and load it
git clone https://github.com/younader/dnnr.git
cd dnnr
pip install -U pip wheel poetry
poetry install
make test                 # to run the tests

If you use this library for a scientific publication, please use the following BibTex entry to cite our work:

@InProceedings{pmlr-v162-nader22a,
  title = 	 {{DNNR}: Differential Nearest Neighbors Regression},
  author =       {Nader, Youssef and Sixt, Leon and Landgraf, Tim},
  booktitle = 	 {Proceedings of the 39th International Conference on Machine Learning},
  pages = 	 {16296--16317},
  year = 	 {2022},
  editor = 	 {Chaudhuri, Kamalika and Jegelka, Stefanie and Song, Le and Szepesvari, Csaba and Niu, Gang and Sabato, Sivan},
  volume = 	 {162},
  series = 	 {Proceedings of Machine Learning Research},
  month = 	 {17--23 Jul},
  publisher =    {PMLR},
  pdf = 	 {https://proceedings.mlr.press/v162/nader22a/nader22a.pdf},
  url = 	 {https://proceedings.mlr.press/v162/nader22a.html},
}