1 Introduction
Over the years,
Next Basket Recommendation (NBR) has received a considerable amount of interest from the research community [
6,
33,
43]. Baskets, or sets of items that are purchased or consumed together, are pervasive in many real-world services, with e-commerce and grocery shopping as prominent examples [
18,
32]. Given a sequence of baskets that a user has purchased or consumed in the past, the goal of an NBR system is to generate the basket of items that the user would like to purchase or consume next. Within a basket, items have no temporal order and are equally important. A key difference between NBR and session-based or sequential item recommendations is that NBR systems need to deal with multiple items in one set. Therefore, models designed for item-based recommendation are not fit for basket-based recommendation, and dedicated NBR methods have been proposed [
16,
20,
21,
25,
31,
34,
41,
43].
1.1 Types of Recommendation Methods
Over the years, we have seen the development of a wide range of recommendation methods.
Frequency-based methods continue to play an important role, as they are able to capture global statistics concerning popularity of items; this holds true for item-based recommendation scenarios as well as for NBR scenarios. Similarly,
nearest neighbor based methods have long been used for both item-based and basket-based recommendation scenarios. More recently, deep learning techniques have been developed to address sequential item recommendation problems, building on the capacity of deep learning based methods to capture hidden relations and automatically learn representations [
7]. Recent years have also witnessed proposals to address different aspects of the NBR task with deep learning based methods, such as item-to-item relations [
25], cross-basket relations [
44], and noise within a basket [
31].
Recent analyses indicate that deep learning based approaches may not be the best performing for all recommendation tasks and under all conditions [
22]. For the task of generating a personalized ranked list of items, linear models and nearest neighbor based approaches outperform deep learning based methods [
14]. For sequential recommendation problems, deep learning based methods may be outperformed by simple nearest neighbor or graph-based baselines [
15]. What about the task of NBR? Here, the unit of retrieval—a basket—is more complex than in the recommendation scenarios considered in other works [
14,
15,
22], with complex dependencies between items and baskets, across time, thus creating a potential for sophisticated representation learning based approaches to NBR to yield performance gains. In this article, we take a closer look at the field to see if this is actually true.
1.2 A New Analysis Perspective
We find important gaps and flaws in the literature on NBR. These include weak or missing baselines, the use of different datasets in different papers, and of non-standard metrics. We evaluate the performance of three families of state-of-the-art NBR models (frequency based, nearest neighbor based, and deep learning based) on three benchmark datasets, and find that no NBR method consistently outperforms all other methods across all settings.
Given these outcomes, we propose a more thorough analysis of the successes and failures of NBR methods. As we show in Figure
1, baskets recommended in an NBR scenario consist of
repeat items (items that the user has consumed before, in previous baskets) and
explore items (items that are new to the user). The novelty of recommended items has been studied before, and related metrics have also been proposed [
36], but novelty-oriented metrics are not NBR specific and only focus on one aspect (i.e., evaluating the novelty of the list of recommendations). To improve our understanding of the relative performance of NBR models, especially regarding repeat items and explore items, we introduce a set of task-specific metrics for NBR. Our newly proposed metrics help us understand which types of items are present in the recommended basket and assess the performance of NBR models when proposing new items vs. already-purchased items.
1.3 Main Findings
Equipped with our newly proposed metrics for NBR, we repeat our large-scale comparison of NBR models and arrive at the following important findings:
•
No NBR method consistently outperforms all other methods across different datasets.
•
All published methods are heavily skewed toward either repetition or exploration compared to the ground truth, which might harm long-term engagement.
•
There is a large NBR performance gap between repetition and exploration; repeat item recommendation is much easier.
•
In many settings, deep learning based NBR methods are outperformed by frequency-based baselines that fill a basket with the most frequent items in a user’s history, possibly complemented with items that are most frequent across all users.
•
A bias toward repeat items accounts for most of the performance gains of recently published methods, even though many complex modules or strategies specifically target explore items.
•
We propose a new protocol for evaluating NBR methods, with a new frequency-based NBR baseline as well as new metrics to assess the potential performance gains of NBR methods.
•
Existing NBR methods have different treatment effects on user performance and item exposure for users with different repetition ratios and items with different frequencies, respectively.
Overall, our work sheds light on the state of the art of NBR, provides suggestions to improve our evaluation methodology for NBR, helps us understand the reasons underlying performance differences, and provides insights to inform the design of future NBR models.
4 Performance Comparison Using Conventional Metrics
4.1 Conventional NBR Metrics
To analyze the performance of NBR methods, we first consider three conventional metrics: recall, Normalized Discounted Cumulative Gain (NDCG) and Personalized Hit Ratio (PHR), all of which are commonly used in previous NBR studies [
20,
21,
44]. We do not consider the F1 and Precision metrics in this article, since we focus on the basket recommendation with a fixed basket size
\(K\), which means the Precision@
\(K\) and F1@
\(K\) are proportional to Recall@
\(K\) for each user. F1@
\(K\) and Precision@
\(K\) are more suitable for NBR with a dynamic basket size for each user. Notations used throughout this work are presented in Table
3.
Recall measures the ability to find all relevant items and is calculated as follows:
where
\(P_{u_j}\) is the predicted basket with
\(K\) recommended items and
\(T_{u_j}\) is the ground-truth basket for user
\(u_j\). The average recall score of all users is adopted as the recall performance.
NDCG is a ranking quality measurement metric, which takes item order into consideration and it is calculated as follows, for a user
\(u \in U\) and its ground-truth basket
\(T_u\):
where
\(p_k\) equals 1 if
\(P_{u_j}^k\in T_u\), and otherwise
\(p_k=0\).
\(P_u^k\) denotes the
\(k\)-th item in the predicted basket
\(P_u\). The average score across all users is the NDCG performance of the algorithm.
PHR focuses on user-level performance and calculates the ratio of predictions that capture at least one item in the ground-truth basket as follows:
where
\(N\) is the number of test users, and
\(\varphi (P_{u_j}, T_{u_j})\) returns 1 when
\(P_{u_j} \cap T_{u_j} \ne \emptyset\) and otherwise returns 0.
4.2 Results with Conventional NBR Metrics
Performance results for the conventional NBR metrics are shown in Table
4. The performance of different methods varies across datasets; there is no method that consistently outperforms all other methods, independent of dataset and basket size. This calls for a further analysis of the factors impacting performance, which we conduct in the next section.
Among the frequency-based baselines, P-TopFreq outperforms G-TopFreq in all scenarios, which indicates that personalization improves the NBR performance. P-TopFreq can only recommend items that have appeared in a user’s previous baskets. As pointed out in Section
3.2, the number of repeat items of a user may be smaller than the basket size, which means there might be empty slots in a basket recommended by P-TopFreq. Despite this limitation, P-TopFreq is a competitive NBR baseline. GP-TopFreq makes full use of the available basket slots by filling any slots with top-ranked items suggested by G-TopFreq. GP-TopFreq outperforms P-TopFreq with no surprise, and, as expected, the difference shrinks as the repetition ratio of the dataset increases. For future fair comparisons, we believe that GP-TopFreq should be the baseline for every NBR method to compare with, especially in high exploration scenarios, to be able to determine what value is added beyond simple frequency-based recommendations.
As to the nearest neighbor based methods, we see that TIFUKNN and UP-CF@r have a similar performance across different scenarios and outperform all frequency-based baselines. The two methods are similar in the sense that both model temporal information, combined with a user-based nearest neighbor method. Their performance in a high exploration scenario is lower than several deep learning based methods (i.e., the TaFeng dataset), but on the Dunnhumby and Instacart datasets, which have a relatively low exploration ratio, they are among the best-performing methods.
Most of the deep learning based methods outperform G-TopFreq, which is the only frequency-based baseline considered in many papers. Surprisingly, P-TopFreq and GP-TopFreq achieve a highly competitive performance and outperform four deep learning based methods (i.e., Dream, Beacon, CLEA, and Sets2Sets) by a large margin in the Dunnhumby and Instacart datasets, where the improvements in terms of \(Recall@10\) range from 35.8% to 141.9% and from 53.6% to 353.3%, respectively. Moreover, the proposed GP-TopFreq baseline outperforms the deep learning based Beacon, Dream, and CLEA algorithms on the TaFeng dataset, the scenario with a high exploration ratio. Of the deep learning based methods, DNNTSP is the only one to have consistently high performance in all scenarios.
4.3 Upshot
Based on the preceding experiments and analysis, we conclude that the choice of dataset plays an important role in evaluating the performance of NBR methods, and no state-of-the-art NBR method is able to consistently achieve the best performance across datasets.
Several deep learning based NBR methods [
25,
31,
43] aim to learn better performing representations by capturing long-term temporal dependencies, denoising, and so forth. They do indeed outperform the G-TopFreq baseline, but many are inferior to the P-TopFreq baseline, especially in datasets with a relatively high repetition ratio. The proposed GP-TopFreq baseline in some sense “re-calibrates” the improvements reported for recently introduced complex, deep learning based NBR methods; compared to the simple GP-TopFreq baseline, their improvements are modest or even absent.
8So far, we have used conventional metrics to examine the performance of NBR methods. To account for the findings reported in this section and provide insights for future NBR method development, we will now consider additional metrics.
5 Performance W.R.T. Repetition and Exploration
To understand which factors contribute to the overall performance of an NBR method, we dive deeper into the basket components from a repetition and exploration perspective.
5.1 Metrics for Repetition vs. Exploration
We propose several metrics that are meant to capture repetition and exploration aspects of a basket. First, we adopt widely used definitions of repetition and exploration in the recommender systems literature [
2,
10,
11,
36] to define what constitutes a repeat item and an explore item in the context of NBR. Specifically, an item
\(i^r\) is considered to be a
repeat item for a user
\(u_j\) if it appears in the sequence of the user’s historical baskets
\(S_j\)—that is, if
\(i^r \in I_{j, t}^\mathit {rep} = {B_j^1 \cup B_j^2 \cup \cdots \cup B_j^t}\). Otherwise, the item is an
explore item, denoted as
\(i^e \in I_{j, t}^\mathit {expl} = I - I_{j, t}^\mathit {rep}\). We write
\(P_{u_j}=P_{u_j}^\mathit {rep} \cup P_{u_j}^\mathit {expl}\) for the predicted next basket
\(B_j^{t+1}\), which is the union of
repeat items \(P_{u_j}^\mathit {rep}\) and
explore items \(P_{u_j}^\mathit {expl}\). As an edge case, a basket may consist of repeat or explore items only.
Novelty of recommendation is a concept that is similar to, but different from, the notion of exploration that we use in this work. Several novelty-related metrics have been proposed (i.e., EPC and EPD [
36]). It is important to note that these metrics are not suitable for our analysis in this article. First, they only focus on measuring the novelty of a ranked list, whereas we want to not only understand the components within the predicted basket but also analyze a model’s ability to fulfill a user’s needs w.r.t. repetition and exploration. Second, these metrics are not NBR specific and only focus on one aspect (i.e., novelty), whereas we want to make a comparison between repetition and exploration to assess the NBR performance.
To analyze the composition of a predicted basket, we propose the
repetition ratio,
\(\mathit {RepR}\), and the
exploration ratio,
\(\mathit {ExplR}\).
\(\mathit {RepR}\) and
\(\mathit {ExplR}\) represent the proportion of
repeat items and
explore items in a recommended basket, respectively. The overall
\(\mathit {RepR}\) and
\(\mathit {ExplR}\) scores are calculated over all test users as follows:
9where
\(N\) denotes the number of test users;
\(K\) is the size of the model’s predicted basket for user
\(u_j\); and
\(P_{u_j}^\mathit {rep}\) and
\(P_{u_j}^\mathit {expl}\) are the sets of repeat items in
\(P_{u_j}\) and of explore items in
\(P_{u_j}\), respectively.
Next, we pay attention to a basket’s ability to fulfill a user’s need for repetition and exploration, and propose the following metrics.
\(\mathit {Recall}_\mathit {rep}\) and
\(\mathit {PHR}_\mathit {rep}\) are used to evaluate the
\(\mathit {Recall}\) and
\(\mathit {PHR}\) w.r.t. the repetition performance; similarly, we use
\(\mathit {Recall}_\mathit {expl}\) and
\(\mathit {PHR}_\mathit {expl}\) to assess the exploration performance. More precisely:
and
where
\(N_r\) and
\(N_e\) denote the number of users whose ground-truth basket contains
repeat items and
explore items, respectively;
\(\varphi (P, T)\) returns 1 when
\(P\cap T \ne \emptyset\) and otherwise returns 0.
Next, we first use the repetition ratio and exploration ratio to examine the recommended baskets; we then use our repetition and exploration metrics to re-assess the NBR methods that we consider, examine how repetition and exploration contribute to the overall recommendation performance, and how users with different degrees of repeat behavior benefit from different NBR methods.
5.2 The Components of a Recommended Basket
We analyze the components of the recommended basket for each NBR method to understand what makes up the recommendation. The results are shown in Figure
2. First, we see that, averaged over all users, all recommended baskets are heavily skewed toward either item repetition or exploration, relative to the ground-truth baskets that are much more balanced between already seen and new items. We can divide the methods that we compare into repeat-biased methods (i.e., P-TopFreq, GP-TopFreq, Sets2Sets, DNNTSP, UP-CF@r, and TIFUKNN) and explore-biased methods (i.e., G-TopFreq, Dream, Beacon, and CLEA). Importantly, a large performance gap exists between the two types. None of the published NBR methods can properly balance the repeat items and explore items of users’ future interests. Figure
3 shows the repetition ratio
\(\mathit {RepR}\) distribution for the ground-truth basket and the recommended basket derived by a repeat-biased method or an explore-biased method. We show the
\(\mathit {RepR}\) distribution of a representative explore-biased method (i.e., CLEA) and a representative repeat-biased method (i.e., DNNTSP) in Figure
3. The
\(\mathit {RepR}\) distribution of the other eight NBR methods are provided in the appendix (see Figure
7).
Among the explore-biased methods, G-TopFreq is not a personalized method; it always provides the most popular items. Dream, Beacon, and CLEA treat all items without any discrimination, which means the explore items are more likely to be in the predicted basket and their basket components are similar to G-TopFreq. Looking at the performance in Table
4, we see that repeat-biased methods generally perform much better than explore-biased methods on conventional metrics across the datasets, especially when the dataset has a relatively high repetition ratio.
The repetition ratios of P-TopFreq and GP-TopFreq serve as the upper bound repetition ratio for the recommended basket. Most baskets recommended by repeat-biased methods are close to or reach this upper bound, even when the datasets have a low ratio of repeat behavior in the ground truth, except for two cases (Sets2Sets and DNNTSP on the TaFeng dataset).
Finally, the exploration ratio of repeat-biased methods increases from basket size 10 to 20; we believe that this is because there are simply no extra repeat items available: it does not mean that the methods actively increase the exploration ratio in a larger basket setting.
5.3 Performance w.r.t. Repetition and Exploration
The results in terms of repetition and exploration performance are shown in Table
5. First of all, using our proposed metrics, we observe that the repetition performance
\(\mathit {Recall}_\mathit {rep}\) is always higher than the exploration performance, even when the explore items form almost 90% of the recommended basket. This shows that the repetition task (recommending repeat items) and the exploration task (recommending explore items) have different levels of difficulty and that capturing users’ repeat behavior is much easier than capturing their explore behavior.
Three deep learning based methods perform worst w.r.t. repeat item recommendation and best w.r.t. explore item recommendation at the same time, as they are heavily skewed toward explore items. We also see that there are improvements in the exploration performance compared to G-TopFreq with the same level of exploration ratio, which indicates that the representation learned by these methods does capture the hidden sequential transition relationship between items. Repeat-biased methods perform better w.r.t. repetition in all settings, since the baskets they predict contain more repeat items. Similarly, we can see that DNNTSP, UP-CF@r, and TIFUKNN perform better than P-TopFreq w.r.t. repeat performance with the same or a lower level of repetition ratio.
Third, explore-biased methods spend more resources on the more difficult and uncertain task of explore item prediction, which is not an optimal choice when considering the overall NBR performance. Being biased toward the easier task of repeat item prediction leads to gains in the overall performance, which is positively correlated with the repetition ratio of the dataset.
To understand the potential reasons for a method being repeat biased or explore biased, we provide an in-depth analysis of the methods’ architectures. P-TopFreq and GP-TopFreq are repeat-biased methods, as they both mainly rely on the frequency of historical items to recommend the next basket. Two nearest neighbor based methods (i.e., TIFUKNN and UP-CF@r) have a module to model both the frequency and the recency of historical items; besides, they both have a parameter to emphasize the frequency and recency information. Similarly, Sets2Sets is also repeat biased, as it adds the historical items’ frequency information to the prediction layer. DNNTSP does not consider frequency information; however, it has an indicator vector to indicate whether an item has appeared in the historical basket sequence or not, which can be regarded as a repeat item indicator. G-TopFreq is explore biased since it is not a personalized method and can only recommend top-K popular items within the dataset. The remaining three explore-biased methods (Dream, Beacon, and CLEA) do not consider the frequency of historical items or the indicator of items’ appearance, so they fail to identify the benefits of recommending repeat items.
5.4 The Relative Contribution of Repetition and Exploration
Even though a clear improvement w.r.t. either repeat or explore performance can be observed in the previous section, this does not mean that this improvement is the reason for the better overall performance, since repeat and explore items account for different ground-truth proportions in different datasets. To better understand where the performance gains of the well-performing methods in Table
4 come from, we remove
explore items and keep
repeat items in the predicted basket to compute the contribution of repetition, and similarly, we remove
repeat items and keep
explore items to compute the performance, which can be regarded as the contribution of exploration.
Experimental results on three datasets are shown in Figure
4. We consider G-TopFreq, P-TopFreq, and GP-TopFreq as simple baselines to compare with. From Figure
4, we conclude that Dream and Beacon perform better than G-TopFreq on the TaFeng dataset, as the main performance gain is from improvements in the exploration prediction. As a consequence, in the Dunnhumby and Instacart datasets, Dream, Beacon, and G-TopFreq achieve similar performance, and the repeat prediction contributes the most to the overall performance, even when their recommended items are heavily skewed toward explore items. Additionally, we observe that CLEA outperforms other explore-biased methods due to its improvements in the repetition performance without sacrificing the exploration performance.
At the same time, it is clear that TIFUKNN, UP-CF@r, Sets2Sets, and DNNTSP outperform explore-biased methods because of the improvements in the repetition performance, even at the detriment of exploration. The repeat items make up the majority of their correct recommendations. Specifically, repeat recommendations contribute to more than 97% of their overall performance on the Dunnhumby and Instacart datasets.
An interesting comparison is between Sets2Sets and P-TopFreq. The strong performance gain of Sets2Sets on the TaFeng dataset is mainly due to the exploration part, whereas P-TopFreq outperforms it by a large margin on the other two datasets at the same level of repetition ratio, even though the personal frequency information is considered in the Sets2Sets model. We believe this indicates that the loss on repeat items seems to be suppressed by the loss on explore items during the training process, which weakens the influence of the frequency information.
Recall that the number of repetition candidates for a user may be smaller than the basket size, which means that there might be empty slots in the basket recommended by P-TopFreq. From Figure
2 and Table
2, we observe that the empty slots account for a significant proportion of exploration slots in many settings. However, existing studies omit this fact when making the comparison with P-TopFreq, leading to an unfair comparison and overestimation of the improvement, as their predictions leverage more slots. For example, Dream, Beacon, and CLEA can beat P-TopFreq, but they are inferior to GP-TopFreq. TIFUKNN and UP-CF@r model the temporal order of the frequency information, leading to a higher repetition performance than P-TopFreq in general. Even though the contribution of the repetition performance improvement is obvious on the Instacart dataset, it is less meaningful on the other two datasets, where the performance gain is mainly from the exploration part by filling the empty slots. When compared with the proposed GP-TopFreq baseline on the TaFeng and Dunnhumby datasets, the improvement is around a modest 3%.
DNNTSP is always among the best-performing methods across the three datasets and is able to model exploration more effectively than other repeat-biased methods. Moreover, it also actively recommends explore items rather than being totally biased toward the repeat recommendation in high exploration scenarios. However, the improvement is limited due to the relatively high repetition ratios and the huge difficulty gap between repetition and exploration tasks. Compared with GP-TopFreq, the improvement of DNNTSP w.r.t. \(\mathit {Recall}@10\) on the Dunnhumby and Instacart datasets is merely 1.3% and 1.9%, respectively, which is modest considering the complexity and training time added by DNNTSP.
Obviously, even though many advanced NBR algorithms learn rich user and/or item representations, the main performance gains stem from the prediction of repeat behavior. Yet, limited progress w.r.t. overall performance has so far been made compared to the simple P-TopFreq and GP-TopFreq baseline methods.
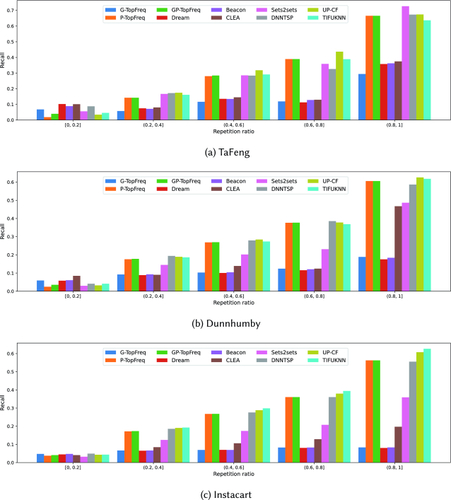
5.5 Treatment Effect for Users with Different Repetition Ratios
As the average repetition ratio in a dataset has a significant influence on a model’s performance (see Section
4), existing NBR methods are skewed to repetition or exploration (see Section
5.2), and global trend might influence the users’ repetition patterns, it is of interest to investigate the treatment effect for users with different repetition ratios. We examine the performance of NBR methods w.r.t. different groups of users with different repetition ratios. We divide the users into five groups according to their repetition ratio
\(([0, 0.2]\),
\((0.2, 0.4]\),
\((0.4, 0.6]\),
\((0.6, 0.8]\),
\((0.8, 1]\)) and calculate the average performance within each group. Note that the repetition ratio indicates the user’s preference w.r.t.
repeat items and
explore items (e.g., users with a low repetition ratio prefer to purchase new items in their next basket). The results are shown in Figure
5.
First, we can see that the methods’ performance within different user groups is different from the performance computed over all users (see Table
4). For example, several explore-biased methods (G-TopFreq, Dream, Beacon, CLEA) can outperform recent repeat-biased methods (TIFUKNN, UP-CF@r, Sets2Sets, DNNTSP) in the user group with a low repetition ratio
\(([0, 0.2])\), but these explore-biased methods are inferior to the repeat-biased methods when computing the performance over all users. Second, the performance of repeat-biased NBR models increases as the repetition ratio increases. Interestingly, we observe an analogous trend w.r.t. the performance of explore-biased NBR methods as the repetition ratio increases, but the rate of the increase is smaller. We believe that this is because the NBR task gets easier for users with a higher repetition ratio, and the repeat-biased methods benefit more from an increase in repetition ratio.
From the perspective of user group fairness, explore-biased methods seem to be fairer than repeat-biased methods across different user groups, as they have quite similar performance across groups. Explore-biased methods have lower variation in performance than repeat-biased methods. However, we should be aware of intrinsic difficulty gaps between different user groups (e.g., it is easier for NBR methods to find correct items for users who like to repeat a purchase). Taking this into consideration, we take G-TopFreq and GP-TopFreq as two anchor baselines to evaluate whether recent NBR methods put a specific user group at a disadvantage or not. On the TaFeng and Dunnhumby datasets, repeat-biased methods (Sets2Sets, UP-CF, TIFUKNN, DNNTSP) fail to achieve the performance of G-TopFreq within users whose repetition ratio is in \([0, 0.2]\), which means they do not cater to users of this group. At the same time, recent explore-biased methods (Dream, Beacon, CLEA) fail to achieve the performance derived by the very simple baseline (i.e., GP-TopFreq) on four user groups on TaFeng, Dunnhumby, and Instacart datasets. This analysis indicates that both repeat-biased and explore-biased NBR methods do not treat all user groups fairly.
5.6 Looking Beyond the Average Performance
In the recommender systems literature, it is customary to compute the average performance over all test users to represent the performance of a recommendation method. Given the diverse treatment effect across different user groups, we want to drill down and see how much the different user groups contribute toward the overall average performance. As before, we use five groups as defined in Section
5.5 in terms of the repetition ratio. Specifically, for each individual group
\(g_j\), we analyze its
proportion of all users (
\(\mathit {PAU}\)) and its
contribution to the average performance (
\(\mathit {CAP}\)) as follows:
where
\(U_{g_j}\) denotes the set of users in group
\(g_j\),
\(q\) denotes the number of user groups, and
\(\mathit {Perf}_u\) represents the method’s performance w.r.t. user
\(u\). Note that the performance metric we analyze in this section is
\(Recall@10\), but similar phenomena can be observed for other metrics.
The results in terms of
\(\mathit {PAU}\) and
\(\mathit {CAP}\) are shown in Table
6. Under the ideal circumstances, the contribution to the average performance
\(\mathit {CAP}\) of each user group should be equal to its proportion of all users
\(\mathit {PAU}\); this would allow us to use the average performance of a method as its overall performance and leave no user group behind. However, we can see that
\(\mathit {CAP}_{(0.8, 1]}\) is much higher than
\(\mathit {PAU}_{(0.8, 1]}\) and
\(\mathit {CAP}_{[0, 0.2]}\) is much lower than
\(PAU_{[0, 0.2]}\) for every NBR method (both repeat-biased methods and explore-biased methods) on all datasets. On the TaFeng dataset, only 5.5% of the users belong to group
\((0.8, 1]\). However, their contribution to the average performance ranges from 18.8% to 36.8%. On the Dunnhumby dataset, 31.4% of the users belong to group
\([0, 0.2]\), whereas the
\(\mathit {CAP}_{[0, 0.2]}\) for repeat-biased methods (i.e., P-TopFreq, GP-TopFreq, Sets2Sets, DNNTSP, TIFUKNN, and UP-CF@r) only ranges from 3.1% to 5.0%. The results reflect that there might be a long-tail distribution w.r.t. the user’s contribution to the average performance (i.e., few users contribute a large proportion to the performance), since the NBR task for different users might have different difficulty levels.
Given the previous observations, we construct a simple example to demonstrate the potential limitations of average performance. Assume we have two user groups (i.e., group
\(g_a\) with 10 users and group
\(g_b\) with only 1 user), where the NBR task for
\(g_b\) is easier than
\(g_a\). Assume also that we have a baseline method
\(M_b\) whose performance
\(\mathit {Perf}\) can achieve 0.02 in group
\(g_a\) and 0.4 in group
\(g_b\). We have another two optimized methods,
\(M_{\alpha }\) and
\(M_{\beta }\). Compared to baseline
\(M_b\),
\(M_{\alpha }\) can achieve 100% improvement in group
\(g_a\), and
\(M_{\beta }\) can also achieve 100% improvement in group
\(g_b\) at the cost of 50% reduction in group
\(g_a\). In this case, the cumulative improvement of
\(M_{\alpha }\) is
\(0.02 \times 10=0.2\), whereas the cumulative improvement of
\(M_{\beta }\) is
\(0.4 \times 1 - 0.01 \times 10 = 0.3\).
\(M_{\beta }\) is considered to be better than
\(M_{\alpha }\) since
\(M_{\beta }\)’s average performance is higher. However, we notice that
\(M_{\alpha }\) can improve the performance of 10 users, whereas
\(M_{\beta }\) can only improve the performance of 1 user and at the detriment of the other 10 users. To sum up, the average performance has limitations to represent the performance of methods on the NBR task, and it might put users in a specific group at a disadvantage.
10 We should calculate the performance of each user group to have a comprehensive understanding of the NBR method.
5.7 Treatment Effect for Items with Different Frequencies
The NBR scenario can be thought of in terms of a two-sided market with items and users [
8,
30,
38]. So far, we have analyzed the user-side performance from several aspects. In this section, we analyze treatment effects of NBR methods from the item side. Specifically, we investigate the relation between an item’s exposure and its frequency in training labels (the ground-truth items of the training users) or test inputs (the historical items of the test users). As the item exposure in recommended baskets and the item frequency have different scales, we use the exposure and frequency of all items, respectively, to normalize them. To visualize the relation between an item’s exposure and its frequency, we rank items according to their frequency and select the top-500 items. The frequency and the exposure distributions for different methods on the TaFeng dataset are shown in Figure
6.
11First, we observe the long-tail distribution w.r.t. the item exposure in all NBR methods; a small number of items get a large proportion of the total exposure. Surprisingly, a large proportion of items do not get any exposure in the baskets recommended by Dream, Beacon, and CLEA on the TaFeng dataset, which we consider to be sub-optimal from the item perspective. Second, the item exposure distributions of P-TopFreq, TIFUKNN, and UP-CF@r are more related to the frequency distribution of the test input than to the frequency distribution of the training labels. We believe that the repeat-biased nature of those algorithms, as well as the absence of training, results in recommendations that are strongly dependent on the items’ frequency in historical baskets (i.e., on the test inputs). Third, in deep learning based methods (Dream, Beacon, CLEA, Sets2Sets, and DNNTSP), we can see that the distribution of items with high exposure shifts to the left, from Figure
6(b) to Figure
6(a). This result reflects the fact that an item’s high exposure is more closely related to its high frequency in the training labels. To sum up, the item frequency distributions in the training labels and test inputs have a different impact on the item exposure of different NBR methods.
5.8 Upshot
Based on our second round of analyses of state-of-the-art NBR methods that we conducted with purpose-built metrics, we observe that there is a clear difficulty gap and tradeoff between the repetition task and the exploration task. As a rule of thumb, being biased toward the easier repetition task is an important strategy that helps to boost the overall NBR performance. Deep learning based methods do not effectively exploit the repetition behavior. Indeed, they achieve a relatively good exploration performance, but they are not able to outperform the simple frequency baseline GP-TopFreq in several cases. Some recent state-of-the-art NBR methods are skewed toward the repetition task and outperform GP-TopFreq. However, the improvements they achieve are limited, especially considering the complexity and computational costs (e.g., for the training process [
44] and for hyper-parameters search [
16,
21]).
Moreover, current NBR methods usually focus on improving the overall performance, but they often fail to provide, or exploit, deeper insights into the components of their recommended baskets (skewed toward repetition or exploration).
Furthermore, different NBR methods have different treatment effects across different user groups, and the widely used average performance cannot fully evaluate the models’ performance—for example, methods might achieve high overall performance at the detriment of a specific user group, which accounts for a large proportion of all users. From the item-side perspective, few items account for a large proportion of the total exposure in all NBR methods, and some NBR methods might only recommend a small set of items to users.
6 Conclusion
We have re-examined the reported performance gains of deep learning based methods for the NBR task over frequency-based and nearest neighbor based methods. We analyzed state-of-the-art NBR methods on the following seven aspects: (i) the overall performance on different scenarios, (ii) the basket components, (iii) the repeat and explore performance, (iv) the contribution of repetition and exploration to the overall performance, (v) the treatment effect for different user groups, (vi) the potential limitations of the average metrics, and (vii) the treatment effect for different items.
6.1 Main Findings
We arrived at several important findings. First, no state-of-the-art NBR method, deep learning based or otherwise, consistently shows the best performance across datasets. Compared to a simple frequency-based baseline, the improvements are modest or even absent. Second, there is a clear difficulty gap and tradeoff between the repeat task and the explore task. As a rule of thumb, being biased toward the easier repeat task is an important strategy that helps to boost the overall NBR performance. Third, some NBR methods might achieve better average overall performance at the detriment of a user group with a large proportion of users. Fourth, deep learning based methods do not effectively exploit repeat behavior. They indeed achieve relatively good explore performance but are not able to outperform the simple frequency-based baseline GP-TopFreq in terms of the relatively easy repetition task. Some state-of-the-art NBR methods are skewed toward the repeat task, and because of this they are able to outperform GP-TopFreq; however, their improvements are limited, especially considering their added complexity and computational costs.
6.2 Insights for NBR Model Evaluation
Our work highlights the following important guidelines that practitioners and researchers working on NBR should follow when evaluating or designing an NBR model. First, use a diverse set of datasets for evaluation, with different ratios of repeat items and explore items. Second, use GP-TopFreq as a baseline when evaluating NBR methods. Third, apart from the conventional accuracy-based metrics, consider the newly introduced repeat and explore metrics, \(\mathit {Recall}_\mathit {rep}\), \(\mathit {PHR}_\mathit {rep}\), \(\mathit {Recall}_\mathit {expl}\), and \(\mathit {PHR}_\mathit {expl}\), as a set of fundamental metrics to understand the performance of NBR methods. Fourth, the \(\mathit {RepR}\) and \(\mathit {ExplR}\) statistics should be included to understand what kind of items shape the recommended baskets. Fifth, calculate the performance of each user group to get a comprehensive understanding of the NBR methods.
6.3 Insights for NBR Model Design
From the analysis of this article, apart from the difficulty imbalance between the repetition and exploration task, we should also be aware that the repetition recommendation task and exploration recommendation task have different characteristics. For instance, the repetition recommendation task focuses on predicting whether historical items will be repurchased or not, where the frequency and recency of historical items are quite important, and the exploration recommendation task focuses on inferring explore items from a much bigger search space via modeling item-to-item correlations, which deep learning methods might be good at. Therefore, just blindly designing complex NBR models without considering the difference between repetition and exploration might be sub-optimal.
We believe that it is better to separate the repetition recommendation and exploration recommendation in the NBR task (e.g., using frequency and recency to address the repetition task, and using NN-based models to model item-to-item correlations), which not only allows us to address repetition and exploration according to their respective characteristics but also offers the flexibility of controlling repetition and exploration in the recommended basket. Additionally, believe that future NBR methods should be able to combine repetition and exploration based on users’ preferences.
6.4 Limitations
One of the limitations of this study is that we did not consider the training and inference execution time in the article, which is important for the real-world value of methods used for NBR [
4]. We use the original implementations of NBR methods to check their reproducibility and avoid potential mistakes that may come with re-implementations; however, the original implementations are based on different frameworks, which leads to an inability to make a fair execution time comparison. A second limitation is that we only follow the widely used binary definition of repeat items and explore items but do not consider a more fine-grained formalization based on the frequency of historical items, which would allow for a more flexible definition of repetition and analysis. A further limitation is that we only considered the short-term utility of NBR methods: will users be satisfied with their next basket? Limited by our experimental setup, where we replay users’ past behavior, we have ignored any potential long-term effects of having a strong focus on short-term utility by emphasizing repeat items as opposed to, for instance, long-term engagement that, likely, benefits from a certain degree of exploration so as to enable surprise and discovery.
6.5 Future Work
Obvious avenues for future work include addressing the limitations summarized previously. Another important line of future work concerns the use of domain-specific knowledge, either concerning complementarity or substitutability of items or concerning hierarchical relations between items, both of which would allow one to consider more semantically informed notions of repeat consumption behavior [
3] for NBR purposes. In addition, our focus in this article has been on users (i.e., in the sense that we compared methods that produce a basket for a given user), and it would be interesting to consider repetition and exploration aspects of the reverse scenario [
27] (i.e., given an item, who are the users to whose baskets this item can best be added?). Finally, even though we focused on NBR, it would be interesting to contrast our outcomes with an analysis of repeat and explore behavior in traditional sequential recommendation scenarios.