Engineering drawing for beginners
- 1. i Md. Roknuzzaman Department of Civil Engineering, HSTU, Dinajpur E-mail : [email protected] Hajee Mohammad Danesh Science and Technology University Dinajpur, Bangladesh
- 2. i Preface Engineering Drawing is one of the basic courses to study for all engineering disciplines. The primary problem faced in learning and teaching of engineering drawing is the limited availability of text books that focus on the basic rules and specifications in relation to the drawing methods practiced in Bangladesh. This handbook is prepared with the primary aim to elaborate necessary basic rules and regulations of engineering drawing that is necessary for students of every engineering discipline. This book is for beginners to introduce them with different elements of engineering drawing. Several worked-out examples are provided along with every chapter and also every chapter includes some exercise and assignments to be practiced by the learners. The course Engineering Drawing is extremely important as it is the language of engineers, technicians, designers and sanitarians. This handbook is devoted to provide general aspects of engineering drawing like lettering, geometric constructions, dimensioning, scaling, orthographic and isometric projections and sectioning. The handbook is prepared taking aid from a number of textbooks and articles mentioned in bibliography section. Most of the figures are drawn using AutoCAD, a few of them are collected from Google image search and some are taken from the textbooks. For further reading, students are encouraged to refer books which are listed in the bibliography section. Acknowledgement The author is delighted to express his thanks and gratitude to Prof. Md. Ruhul Amin, the honorable Vice-chancellor and chairman of the Department of Civil Engineering, HSTU, without his initiative and inspiration this material would not come into reality. Author is also grateful to his colleagues of the Department of Civil Engineering and of the Department of Agricultural and Industrial Engineering for inspiring him in completing this handbook. And obviously it is the mercy of the Almighty Allah that the material has finally come into a complete form.
- 3. ii CONTENTS Page No. Preface………………………………..…………………………………………………… i Acknowledgement………………………………………………………………………... i Contents…………………………………………………………………………………... ii CHAPTER 1 INTRODUCTION 1.1 Drawing………………………………………………………... 1 1.2 Types of Drawing……………………………………………… 1 1.2.1 Artistic Drawing…...………………………………… 1 1.2.2 Engineering Drawing………………………………… 1 1.3 Purpose of Engineering drawing………………………………. 1 1.4 Applications of Engineering Drawing………………………… 2 1.5 Types of Engineering Drawing……………………………….. 2 1.5.1 Geometric Drawing………………………………….. 2 1.5.2 Mechanical Engineering Drawing…………………… 2 1.5.3 Civil Engineering Drawing…………………………… 2 1.5.4 Electrical Engineering Drawing……………………… 2 1.6 Specific Purposes of Studying Civil Engineering Drawing…… 2 1.7 Types of Civil Engineering drawing…………………………... 3 1.8 Elements of Engineering Drawing…………………………….. 3 1.9 Drawing Standards……………………………………………. 3 1.10 Drawing Instruments…………………………………………. 3 Review Questions…………………………………………………. 9 CHAPTER 2 LINES AND SYMBOLS Objectives………………………………………………………….. 10 2.1 Conventional Lines……………………………………………. 10 2.2 Conventional Symbols………………………………………… 12 2.2.1 Common Geometric Symbols Used in Engineering Drawing…………………………………………………... 12 2.2.2 Common Symbols Used in Civil Engineering Drawing… 13 2.2.3 Common Symbols Used in Electrical Engineering Drawing…………………………………………………... 15 Exercise and Assignments…………………………………………. 16 Review Questions…………………………………………………. 16 CHAPTER 3 LETTERING AND NUMBERING Objectives………………………………………………………….. 17 3.1 Letter Styles……………………………………………………. 17 3.2 Classification of Letters………………………………… 17 3.2.1 Extended and Condensed Letters…………………….. 17 3.2.2 Light Face and Bold Face Letters…………………….. 18 3.3 Technique of Lettering………………………………………… 18 3.4 Guide Lines……………………………………………………. 18 3.4.1 Guidelines for Capital Letters……………………….. 18 3.4.2 Guidelines for Lower-Case Letters………………….. 18 3.5 Single Stroke lettering…………………………………………. 18 3.6 Order of Strokes……………………………………………..... 18 3.7 Spacing of Letters……………………………………………… 22 3.8 Lettering in Maps……………………………………………… 22 3.9 Summary of ISO Rules for Lettering…………………………. 22 Exercise and Assignments…………………………………………. 24 Review Questions…………………………………………………. 24
- 4. iii CHAPTER 4 GEOMETRIC CONSTRUCTION Objectives………………………………………………………….. 25 4.1 Introduction……………………………………………………. 25 4.2 Geometric Nomenclature……………………………………… 25 4.2.1 Points in Space………………………………………... 25 4.2.2 Lines…………………………………………………... 25 4.2.3 Angle………………………………………………….. 25 4.2.4 Triangles………………………………………………. 26 4.2.5 Quadrilateral…………………………………………... 26 4.2.6 Polygon………………………………………………... 26 4.2.7 Circle………………………………………………….. 27 ` 4.2.8 Solids………………………………………………….. 27 4.3 Techniques of Geometric Constructions………………………. 27 4.3.1 How to Bisect a Line or an Arc……………………….. 28 4.3.2 How to Divide a Line into a Number of Equal Parts….. 28 4.3.3 How to Bisect an Angle……………………………….. 29 4.3.4 How to Draw an Arc or Circle (Radius) through Three Given Points…………………………………………… 29 4.3.5 How to Transfer an Odd Shape (Triangular)………….. 30 4.3.6 How to Transfer Complex Shapes……………………. 30 4.3.7 How to Draw a Pentagon (5 Sides)…………………… 31 4.3.8 How to Draw a Hexagon (6 Sides)……………………. 31 4.3.9 How to Draw an Octagon (8 Sides)…………………… 31 4.3.10 How to Draw any Sided Regular Polygon…………… 32 4.3.11 How to Locate the Center of a Given Circle………… 33 4.3.12 How to Draw Arc Tangent to a Straight Line and a Curve………………………………………………… 34 4.3.13 How to Draw Arc Tangent to Two Arcs of Different Radius………………………………………………... 34 4.3.14 How To Draw an Ogee Curve………………………. 35 4.3.15 How to Draw Straight Tangent to Two Arcs of Different Radius……………………………………… 36 4.3.16 How to Draw an Ellipse (Four-centered Approximate Method)………………………………………………. 36 Exercise and Assignments…………………………………………. 37 Review Questions…………………………………………………. 37 CHAPTER 5 DIMENSIONING Objectives………………………………………………………….. 38 5.1 Purpose of Dimensioning..……………………………………. 38 5.2 General Conditions for Dimensioning….…………………….. 38 5.3 Elements of Dimension System………………………………. 38 5.4 Rules for Dimensioning………...……………………………... 38 5.4.1 General Rules for Dimensioning….………………….. 38 5.4.2 Rules of Extension Lines…………………………….. 39 5.4.3 Rules of Dimension Lines…………………….….…... 39 5.4.4 Rules of Arrowhead…………………………………... 39 5.4.5 Rules of Leaders………………………………………. 40 5.5 Direction of Dimensions………………………………………. 40 5.6 Technique of Dimensioning…………………………………… 41 5.7 Dimensioning in Limited Space………………………………. 41 5.8 Dimensioning of Angles………………………………………. 42 5.9 Dimensioning of Arcs…………………………………………. 43 5.10 Dimensioning of Chord length, Arc length and Angle………. 43 5.11 Dimensioning of Round Holes……………………………….. 44 5.12 Dimensioning of Blind Holes………………………………… 44
- 5. iv 5.13 Dimensioning of Chamfer……………………………………. 44 5.14 Common Mistakes in Dimensioning…………...…………….. 45 5.15 Worked-out Examples of Dimensioning……………………... 48 Exercise and Assignments…………………………………………. 51 Review Questions…………………………………………………. 53 CHAPTER 6 SCALES Objectives………………………………………………………….. 54 6.1 Scale…………………………………………………………… 54 6.2 Uses of scale…………………………………………………… 54 6.3 Sizes of Scales…………………………………………………. 54 6.4 Classification of Scales………………………………………... 55 6.4.1 Plain Scale……………………………………………… 55 6.4.2 Diagonal Scale…………………………………………. 55 6.4.3 Comparative Scale…………………………………….. 55 6.4.4 Vernier Scale………………………………………….. 55 6.4.5 Chord Scale……………………………………………. 55 6.5 Necessity of Construction of Scale on Drawing……………… 55 6.6 Information Necessary for Construction of a Scale…………… 56 6.6.1 The Representative Fraction (R.F.)……………………. 56 6.6.1.1 Worked out Examples of R.F. calculation……….. 56 6.6.2 Units of Measurement………………………………….. 57 6.7 Construction of Plain Scale……………………………………. 57 6.7.1 Worked-out Examples of Plain Scale Construction…… 58 6.8 Principle of Diagonal Scales…………………………………... 61 6.9 Construction of Diagonal Scales………………………………. 62 6.9.1 Worked-out Examples of Diagonal Scale Construction... 63 Exercise and Assignments…………………………………………. 70 Review Questions…………………………………………………. 71 CHAPTER 7 PROJECTION Objectives………………………………………………………….. 72 7.1 Introduction……………………………………………………. 72 7.1.1 Projection……………………………………………… 72 7.1.2 Picture Plane/Plane of Projection……………………… 72 7.1.3 View…………………………………………………… 72 7.1.4 Projector……………………………………………….. 72 7.2 Types of projection…………………………………………….. 73 7.2.1 Orthographic Projection……………………………….. 73 7.2.2 Pictorial Projection…………………………………….. 74 7.2.2.1 Axonometric Projection………………………….. 74 7.2.2.2 Oblique Projection……………………………….. 74 7.2.3 Perspective Projection………………………………….. 75 7.3 Details of Orthographic Projection……………………………. 75 7.3.1 The Glass Box method………………………………… 75 7.3.2 The Six Principal Views……………………………….. 77 7.3.3 Arrangement of Views…………………………………. 78 7.3.3.1 Glass Box Concept for 1st Angle Projection…...… 79 7.3.3.2 Glass Box Concept for 3rd Angle Projection…...... 80 7.3.4 Orthographic Projections of Parallel, Inclined and Oblique Surfaces……………………………………….. 81 7.3.5 Orthographic Projections of Hidden Surfaces…………. 82 7.3.6 Orthographic Projections of Curved Surfaces and Holes 82 7.3.7 Precedence of Lines…………………………………… 82 7.3.8 Method of Obtaining Views…………………………… 83 7.3.9 Methods of projecting views…………………………… 84
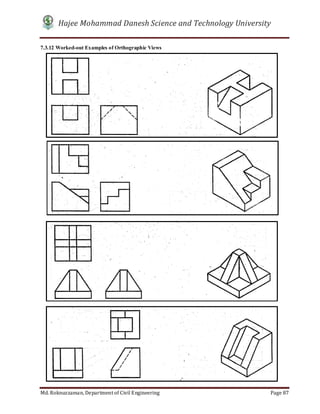
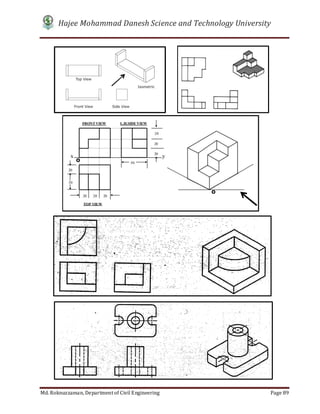
- 6. v 7.3.10 Spacing between the Views………………..………… 84 7.3.11 Steps for Projecting Views by Diagonal Line Method.. 85 7.3.12 Worked-out Examples of Orthographic Views………. 87 7.3.13 Limitation of Multi View Projection…...…………….. 91 7.4 Details of Isometric Projection………………………………… 91 7.4.1 Principle of Isometric Projection………………………. 91 7.4.2 Isometric Scale…………………………………………. 92 7.4.3 Lines in Isometric Projection…………………………... 93 7.4.4 Isometric Drawing……………………………………... 93 7.4.5 Method of Constructing Isometric Drawing…………… 94 7.4.5.1 Box Method……………………………………… 94 7.4.5.2 Off-set Method…………………………………... 94 7.4.6 Isometric Drawing of Planes…………………………... 95 7.4.6.1 Isometric Drawing of Rectangular Plane……….. 95 7.4.6.2 Isometric Drawing of Pentagonal Plane………… 95 7.4.6.3 Isometric Drawing of a Circular Plane………….. 96 7.4.7 Isometric Drawing of Solids…………………………... 96 7.4.7.1 Points to be Remembered for Isometric drawing... 96 7.4.8 Steps for drawing Isometric View…………………….. 96 7.4.9 Worked-out Examples of Isometric Drawing…………. 99 Exercise and Assignments…………………………………………. 102 Review Questions…………………………………………………. 109 CHAPTER 8 SECTIONING 8.1 Introduction……………………………………………………. 110 8.2 Terminology…………………………………………………… 110 8.2.1 Sectioning……………………………………………… 110 8.2.2 Sectional View………………………………………… 110 8.2.3 Cutting Plane…………………………………………… 111 8.2.4 Cutting Plane Line……………………………………... 111 8.2.5 Section Lining…………………………………………. 112 8.3 Types of section……………………………………………….. 112 8.3.1 Full Section…………………………………………….. 113 8.3.2 Offset Section………………………………………….. 113 8.3.3 Half Section……………………………………………. 114 8.3.4 Broken-out Section…………………………………….. 114 8.3.5 Revolved Section………………………………………. 115 8.3.6 Removed Section………………………………………. 117 8.4 Special Consideration for Section of Ribs, Spokes and Lugs………………………………………………………….. 118 8.5 Parts that Should Not Be Sectioned…………………………... 119 8.6 Worked-out Examples of Sectioning………………………….. 120 Exercise and Assignments…………………………………………. 123 Review Questions…………….……………………………………. 125 Bibliography ……………………………………… 126
- 7. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 1 CHAPTER 1 INTRODUCTION 1.1 Drawing The graphical representation of any object or idea can be termed as drawing. A drawing can be prepared either using free hand or using engineering instruments or using computer program. 1.2 Types of Drawing 1. Artistic Drawing 2. Engineering Drawing 1.2.1 Artistic Drawing The drawing representing any object or idea which is sketched in free hand using imagination of artist and in which proper scaling and dimensioning is not maintained is called an artistic drawing. Example: Painting, Posters, arts etc. 1.2.2 Engineering Drawing Engineering drawing can be defined as a graphical language used by engineers and other technical personnel associated with the engineering profession which fully and clearly defines the requirements for engineered items. It is a two dimensional representation of a three dimensional object. In other words, The art of representing a real or imaginary object precisely using some graphics, symbols, letters and numbers with the help of engineering drawing instruments is called engineering drawing. The art of representing engineering objects such as buildings, roads, machines, circuits etc. on a paper is called engineering drawing. It is used by engineers and technologists. An engineering drawing provides all information about size, shape, surface type, materials etc. of the object. Example: Building drawing for civil engineers, Machine drawing for mechanical engineers, Circuit diagrams for electrical and electronics engineers, computer graphics for one and all etc. Table 1.1 Difference Between Artistic and Engineering Drawing Artistic Drawing Engineering Drawing Purpose of artistic drawing is to convey emotion or artistic sensitivity in some way. Purpose of engineering drawing is to convey information about engineering object or idea. Can be understood by all. Need some specific knowledge or training to understand. Scale maintaining is not necessary Scale maintaining is necessary No special requirement of engineering instruments. Engineering drawing instruments is used to make the drawing precise. An artistic drawing may not be numerically specific and informative. An engineering drawing must be numerically specific and informative. Standard drawing code need not to be followed. Standard drawing code (like ISO, ANSI, JIS, BS etc,) must be maintained. 1.3 Purpose of Engineering drawing It is very difficult and complex to explain some certain engineering requirements in word. In such cases well dimensioned and properly scaled graphics can make it easy to understand that for technical personnel. Engineering drawing serves this purpose. Any product that is to be manufactured, fabricated, assembled, constructed, built, or subjected to any other types of conversion process must first be designed. To make the outcome from the design understandable to any third party engineering drawing is the best way.
- 8. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 2 1.4 Applications of Engineering Drawing Engineering drawing is an essential part of almost all engineering projects. Some important uses of engineering drawing are mentioned below: 1. It is used in ships for navigation. 2. For manufacturing of machines, automobiles etc. 3. For construction of buildings, roads, bridges, dams, electrical and telecommunication structures etc. 4. For manufacturing of electric appliances like TV, phone, computers etc. 1.5 Types of Engineering Drawing Engineering drawing can be grouped into following 4 major categories: 1. Geometrical Drawing a. Plane geometrical drawing b. Solid geometrical drawing 2. Mechanical Engineering Drawing 3. Civil Engineering Drawing 4. Electrical & Electronics Engineering drawing etc. 1.5.1 Geometric Drawing The art of representing geometric objects such as rectangles, squares, cubes, cones, cylinders, spheres etc. on a paper is called geometric drawing. If the object has only 2 dimensions i.e. length and breadth (as rectangles, squares, triangles etc.), it is called Plane geometrical drawing and if it has 3 dimensions i.e. length, breadth and thickness/depth (as cube, prism, sphere, cylinder etc.), it is called Solid geometrical drawing. 1.5.2 Mechanical Engineering Drawing The art of representing mechanical engineering objects such as machines, machine parts etc. on a paper are called mechanical engineering drawing or machine drawing. It is used by mechanical engineers to express mechanical engineering works and projects for actual execution. 1.5.3 Civil Engineering Drawing The art of representing civil engineering objects such as buildings, roads, bridges, dams etc. on a paper are called civil engineering drawing. It is used by civil engineers to express civil engineering works and projects for actual execution. 1.5.4 Electrical Engineering Drawing The art of representing electrical engineering objects such as motors, generators, transformers, wiring diagrams etc. on a paper are called electrical engineering drawing. It is used by electrical engineers to express electrical engineering works and projects for actual execution. The art of representing electronic circuits of TV, Phones, computers etc. on a paper are called electronic engineering drawing or electronic drawing. It is used by electronic engineers to express electronic engineering works and projects for actual execution. 1.6 Specific Purposes of Studying Civil Engineering Drawing One needs to study civil engineering drawing for the following purposes: 1. To develop the ability to produce simple civil engineering drawing and sketches based on current practice. 2. To develop the skills to read and understand the drawings used in civil engineering projects. 3. To develop a working knowledge of the layout of buildings, bridges, highways etc. and other civil engineering structures. 4. To develop skills in abstracting information from calculation sheets and schematic diagrams to produce working drawings for masons, construction managers and field workers who execute civil engineering projects.
- 9. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 3 1.7 Types of Civil Engineering drawing Civil engineering drawing of a civil work project can be classified in two broad categories: 1. Architectural Drawing a. Plan: It shows the position of different objects and elements of the structure in a two dimensional view. Only length and width of objects are shown here. b. Elevation and Section: It shows a view along the height of structure. Elevation can be presented in 2D or 3D. In 2D elevation view either height and length or height and width is showed. 2. Structural Drawing It shows the detail requirement of reinforcement and their arrangement in structure. It also shows the specification and properties of construction materials like concrete, steel, timber etc. 1.8 Elements of Engineering Drawing 1.9 Drawing Standards An engineering drawing should be well specified and universally acceptable. That’s why there are some specified rules for engineering drawing. These rules may vary slightly for different regions. There are some drawing standards or drawing codes that accumulates the rules of engineering drawing for a certain region. Well- known drawing codes and their application region is expressed below: Table 1.2 Drawing Standards Country/Region Code/Standard Full Meaning Worldwide ISO International Organization for Standardization USA ANSI American National Standards Institute JAPAN JIS Japanese Industrial Standards UK BS British Standards In Bangladesh in most of the cases, it is usual practice to follow ISO code for engineering drawing. However, in some instances ANSI and BS standards are also followed. 1.10 Drawing Instruments The most common instruments used for engineering drawing are: 1. Drawing Board 4. Rubber/Eraser 7. Instrument box 10. Scales 2. Drawing paper 5. T- square 8. Protractor 11. Pins and clips 3. Pencil 6. Set-square 9. Compass 12. Adhesive tapes 13. French curves etc Drawing Board It is a board or platform rectangular in shape. Size of drawing board need to be larger than that of drawing paper. It is made of wood. Top surface should be smooth. Fig. 1.1 Elements of Engineering Drawing
- 10. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 4 Drawing Paper Drawing paper is the paper, on which drawing is to be made. All engineering drawings are made on sheets of paper of strictly defined sizes, which are set forth in the respective standards. The use of standard size saves paper and ensures convenient storage of drawings. Desirable properties a good drawing paper: It should be smooth and uniform in thickness. It should be thick, strong and tough. Fibers of drawing paper should not be disintegrated when a good eraser is used on it. Paper Types: 1. Detail Paper (used for pencil work). 2. White drawing paper (used for finished drawing) 3. Tracing paper (used for both pencil and ink work and useful for replicating a master copy) Paper Size: Table 1.3 ISO Paper Sizes (plus rounded inch values) Format A series B series C series Size mm × mm in × in mm × mm in × in mm × mm in × in 0 841 × 1189 33.1 × 46.8 1000 × 1414 39.4 × 55.7 917 × 1297 36.1 × 51.1 1 594 × 841 23.4 × 33.1 707 × 1000 27.8 × 39.4 648 × 917 25.5 × 36.1 2 420 × 594 16.5 × 23.4 500 × 707 19.7 × 27.8 458 × 648 18.0 × 25.5 3 297 × 420 11.7 × 16.5 353 × 500 13.9 × 19.7 324 × 458 12.8 × 18.0 4 210 × 297 8.27 × 11.7 250 × 353 9.84 × 13.9 229 × 324 9.02 × 12.8 5 148 × 210 5.83 × 8.27 176 × 250 6.93 × 9.84 162 × 229 6.38 × 9.02 6 105 × 148 4.13 × 5.83 125 × 176 4.92 × 6.93 114 × 162 4.49 × 6.38 7 74 × 105 2.91 × 4.13 88 × 125 3.46 × 4.92 81 × 114 3.19 × 4.49 8 52 × 74 2.05 × 2.91 62 × 88 2.44 × 3.46 57 × 81 2.24 × 3.19 9 37 × 52 1.46 × 2.05 44 × 62 1.73 × 2.44 40 × 57 1.57 × 2.24 10 26 × 37 1.02 × 1.46 31 × 44 1.22 × 1.73 28 × 40 1.10 × 1.57 The tolerances specified in the standard are ±1.5 mm (0.06 in) for dimensions up to 150 mm (5.9 in), ±2 mm (0.08 in) for lengths in the range 150 to 600 mm (5.9 to 23.6 in) and ±3 mm (0.12 in) for any dimension above 600 mm (23.6 in).
- 11. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 5 D Fig. 1.2 Standard Sizes of Drawing Paper : = : √
- 12. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 6 Paper Layout: The ISO standard (ISO 5457) require a 20mm border to the left hand edge (for filing) and a 10mm border round the other three sides of the drawing sheet. However, the margin of paper can be increased according to requirements and settings of printer/plotter. Fig. 1.3 Landscape and Portrait Layout of Drawing Paper Portrait layout Landscape layout
- 13. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 7 For Class Work: Pencil: Pencils are used to draw different lines, shapes, symbols and to write texts in engineering drawing. Based on the hardness of lead pencils are classified in three major grades as hard, medium and soft. They are further sub- divided and numbered as mentioned in table below: Table 1.4 Pencils of Different Grades Selection of proper grade pencil or lead is important for quality drawing. One has to be careful in selecting a lead because very hard lead might penetrate the drawing, on the other hand, soft lead may smear. Quality and type of drawing paper is an important factor in selecting lead. One other importance consideration is the importance of line to be drawn. Inferior lines (like border lines, guide lines, construction lines and any other auxiliary lines needed to be erased later) are drawn using harder pencil. Comparatively softer grade pencil is used for drawing superior items (like object line, texts, symbols etc.). Common uses of different grade pencil are tabulated below: Table 1.5 Pencil Usage Guideline for Different Line Types Task Lead Task Lead Task Lead Border Lines 3H, 2H Centerlines 2H,H Leaders 2H, H Construction Lines 3H, 2H Phantom Lines 2H,H Hidden Lines 2H, H Guide Lines 3H, 2H Long Break Lines 2H, H Cross Hatching Lines 2H,H Lettering H, F, HB Visible Lines H, F, HB Extension Lines 2H, H Dimension Lines 2H, H Cutting Plane Lines H, F, HB Short Break lines H, F, HB For convenience we will use 2H and HB pencils for our assignments and class drawings. Grade Items arranged ordering harder to softer Hard 9H> 8H> 7H>6H>5H>4H Medium 3H>2H>H>F>HB>B Soft 2B>3B>4B>5B>6B>7B Fig. 1.4 Paper Layout for Class Assignments
- 14. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 8 T-square: 1. Used to draw horizontal straight line. 2. Used to guide the triangles when drawing vertical and inclined lines. Set-square: 1. Used to construct the most common angles (i.e. 300 , 450 and 600 ) in technical drawings. 2. Used to draw parallel and perpendicular lines quickly and conveniently. Protractor: It is used for laying out and measuring angle. Scale (ruler): A number of kinds of scales are available for varied types of engineering design. Scales with beveled edges graduated in mm are usually used. Diagonal Scale Fig. 1.5 T-square Fig. 1.6 Set-square Fig. 1.7 Protractor Fig. 1.8 Scales
- 15. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 9 Compass It is used to draw circles and arcs both in pencil and ink. It consists of two legs pivoted at the top. One leg is equipped with a steel needle attached with a screw, and other shorter leg is, provided with a socket for detachable inserts. Dividers: Used chiefly for transferring distances and occasionally for dividing spaces into equal parts. i.e. for dividing curved and straight lines into any number of equal parts, and for transferring measurements. French curve: It is used to draw irregular curves that are not circle arcs. The shape varies according to the shape of irregular curve. Review Questions 1. Define drawing and classify it. 2. What are the differences between engineering drawing and artistic drawing? 3. Why Engineering drawing is called the language of engineers? 4. What are specific applications of engineering drawing for your discipline? 5. Classify engineering drawing and give example of each branch. 6. Classify civil engineering drawing. 7. What is difference between plan, elevation and section? 8. Name some codes/standards of engineering drawing. Which one is used in Bangladesh/USA/UK? 9. Name some common drawing instruments and their uses. 10. What is the standard size of a drawing board? 11. What is the standard proportion of drawing paper’s length and width? 12. What is the measurement of an A0/A1/A2/A3/A4 paper? 13. What is the difference between white drawing paper and tracing paper? 14. How pencils are classified? 15. On what considerations you will choose pencil for a drawing? 16. Which pencil should be used for drawing object boundary/guideline/dimension line/border line/texts. 17. How paper quality affects choice of pencil? 18. Which angles can be drawn directly with set-squares? Fig. 1.9 Compass and Divider Fig. 1.10 French Curves
- 16. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 10 CHAPTER 2 LINES AND SYMBOLS Objectives Objective of studying this chapter are: To learn to explain the different line types To learn to mention the application of each line type in technical drawings To learn to mention the application of different symbols. 2.1 Conventional Lines Each line on a technical drawing has a definite meaning and is drawn in certain ways. There are certain conventional lines recommended by drawing codes. Usually two types of widths are used for the lines; they are thick and thin. Thick lines are in between 0.5 mm to 0.8 mm wide while the thin lines are between 0.3 mm to 0.5 mm wide. However, the exact thickness may vary according to the size and type of drawing. If the size of drawing is larger, the width of the line becomes higher. There should also be a distinct contrast in the thickness of different kinds of lines, particularly between the thick lines and thin lines. Visible, cutting plane and short break lines are thick lines, on the other hand hidden, center, extension, dimension, leader, section, phantom and long break lines are thin. Table 2.1 Conventional Lines and Their Usage Cont. SL No. Name of line type Line appearance Usage 01 Visible line/ Object line To indicate all visible outlines/boundary of an object. It shows the shape of an object 02 Hidden line/ Dashed line To represent hidden edge of an object. They should end on both sides by touching the visible lines and should touch themselves at intersection (if any). 03 Center line To show a line passing through center of hole, pitch line etc. 04 Extension line, Dimension line and leaders To show dimension of an object
- 17. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 11 Table 2.1 Conventional Lines and Their Usage (Contd.) SL No. Name of line type Line appearance Usage 05 Section line To indicate cut portion of an object 06 Cutting plane line To show imaginary cutting of an object. 07 ISO cutting planeline 08 Break lines To show break of an object in order to shorten the view of a long part. 09 Phantom line/ Repeat line To show alternate position of an object or the position of an adjacent part. Fig. 2.1 Use of Different Types of Lines
- 18. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 12 2.2 Conventional Symbols A variety of symbols are used in engineering drawing to represent different elements, properties, material types etc. Some geometric symbols are commonly used in almost every types of drawing while there are some special symbols used in specific types (civil, mechanical, electrical etc.) of drawing. 2.2.1 Common Geometric Symbols used in Engineering Drawing Table 2.2 Conventional Geometric Symbols
- 19. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 13 2.2.2 Common Symbols used in Civil Engineering Drawing Fig. 2.3 Typical Window Types Fig. 2.2 Typical Door Types
- 20. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 14 Fig. 2.4 Symbols for Materials Fig. 2.5 Typical Building Plan
- 21. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 15 2.2.3 Common Symbols used in Electrical Engineering Drawing Fig. 2.6 Typical Symbols for Electrical Engineering Drawing Fig. 2.7 Typical Electrical Symbols Used in Building Drawing
- 22. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 16 Exercise and Assignments 1. Make a table showing the conventional lines most commonly used in engineering drawing mentioning their specific applications. 2. Make a table showing the conventional symbols (geometric/civil/electrical/materials) most commonly used in engineering drawing with their meanings. Review Questions 1. Why have you studied lines and symbols? 2. Draw a standard hidden/ center/ cutting plane/ section/ break line and show an example of its use. 3. What is the standard proportion of solid segments and gaps in a hidden/center line. 4. Why there is no specified proportion for dimension and extension line? 5. What is difference between applicability of a section line and a break line? 6. Which conventional lined are to be drawn with 2H pencils? 7. Which conventional lined are to be drawn with HB pencils? 8. What is the standard symbol to show diameter/ radius/ slope/ datum? 9. What is the standard symbol for single /double opening in/out doors? 10. What is the standard symbol for showing sectioning through earth/ concrete/ brick/ metal/ wood. 11. What is the standard symbol to show inductor/ resistor/ gates? 12. Draw some electrical symbol for household weiring.
- 23. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 17 CHAPTER 3 LETTERING AND NUMBERING Objectives Objectives of studying this chapter are: To know different style of lettering. To learn to write letters and numbers according to the standard 3.1 Letter Styles Gothic Roman Italic Text They were all made with speedball pens, and are therefore largely single-stroke letters. If the letters are drawn in outline and filled in, they are referred to as “filled- in” letters. The plainest and most legible style is the gothic from which our single-stroke engineering letters are derived. The term roman refers to any letter having wide down ward strokes and thin connecting strokes. Roman letters include old romans and modern roman, and may be vertical or inclined. Inclined letters are also referred to as italic, regardless of the letter style; text letters are often referred to as old English. 3.2 Classification of Letters 3.2.1 Extended and Condensed Letters To meet design or space requirements, letters may be narrower and spaced closer together, in which case they are called “Compressed” or “Condensed” letters. If the letters are wider than normal, they are referred to as “Extended” letters. Fig. 3.1 Different Styles of English Letters
- 24. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 18 3.2.2 Light Face and Bold Face Letters Letters also vary as to the thickness of the stems or strokes. Letters having very thin stems are called Light Face Letters, while those having heavy stems are called Bold Face Letters. 3.3 Technique of Lettering “Any normal person can learn to letter if he is persistent and intelligent in his efforts.” While it is true that “Practice makes perfect,” it must be understood that practice alone is not enough; it must be accompanied by continuous effort to improve. There are three necessary steps in learning to letter: Knowledge of the proportions and forms of the letters and the order of the strokes. Knowledge of composition- the spacing of the letters and words. Persistent practice, with continuous effort to improve. 3.4 Guide Lines Extremely light horizontal guidelines are necessary to regulate the height of letters. In addition, light vertical or inclined guidelines are needed to keep the letters uniformly vertical or inclined. Guidelines are absolutely essential for good lettering and should be regarded as a welcome aid, not as an unnecessary requirement. Make guidelines light, so that they can be erased after the lettering has been completed. Use a relatively hard pencil such as a 4H to 6H, with a long, sharp, conical point. 3.4.1 Guidelines for Capital Letters On working drawings, capital letters are commonly made 3mm high, with the space between lines of lettering from ¾ th to the full height of the letters. The vertical guidelines are not used to space the letters (as this should always be done by eye while lettering), but only to keep the letters uniformly vertical, and they should accordingly be drawn at random. A guideline for inclined capital letters is somewhat different. The spacing of horizontal guidelines is the same as for vertical capital lettering. The American Standard recommends slope of approximately 68.20 with the horizontal and may be established by drawing a “sloped triangle”, and drawing the guidelines at random with T-square and triangles. 3.4.2 Guidelines for Lower-Case Letters Lower-case letters have four horizontal guidelines, called the cap line, waistline, and base line and drop line. Strokes of letters that extend up to the cap line are called ascenders, and those that extend down to the drop line, descenders. Since there are only five letters (p, q.g, j, y) that have descenders, the drop lines are little needed and are usually omitted. In spacing guidelines, space “a” may vary from 3/5to 2/3 of space “b”. 27The term single stoke or one stoke does not mean that the entire letter is made without lifting the pencil. But the width of the stroke is the width of the stem of the letter. 3.5 Single Stroke Lettering The salient features of this type of lettering are: Greatest amount of lettering on drawings is done in a rapid single stroke letter i.e. either vertical, or inclined. The ability to letter and perfectly can be acquired only by continued and careful practice it is not a matter of artistic talent or event of dexterity in hand writing 3.6 Order of Strokes They are necessary to have legible and accurate letter styles. In the following description an alphabet of slightly extended vertical capitals has-been arranged in-group. Study the slope of each letter with the order and direction of the storks forming it. The proportion of height and width of various letters must be known carefully to letter them perfectly. The I-H-T Group The letter I is The Foundation Stroke. The top of T is drawn first to the full width of the square and the stem is started accurately at its midpoint.
- 25. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 19 The L-E-F Group The L is made in two strokes. The first two strokes of the E are the same for the L, the third or the upper stoke is lightly shorter than the lower and the last stroke is the third as long as the lower. F has the same proportion as E The V-A-K Group V is the same width as A, the A bridge is one third up from the bottom. The second stroke of K strikes stem one third up from the bottom and the third stroke branches from it. The M-W Group M may be made in consecutive strokes of the two verticals as of N. W is made with two V’s. The O-Q-C-G Group The O families are made as full circles and made in two strokes with the left side a longer arc than the right. A large size C and G can be made more accurately with an extra stroke at the top.29 The D- U-J Group The top and bottom stokes of D must be horizontal, fail line to observe this is a common fault with beginners. U is formed by two parallel strokes to which the bottom stroke be added. J has the same construction as U, with the first stroke omitted. The P-R-B Group The number of stokes depends up on the size of the letter. The middle line of P and R are on centerline of the vertical line. Fig. 3.2 Order of Strokes for Single Stroke Gothic Letters (Uppercase) and Numbers
- 26. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 20 Fig. 3.3 Proportion of Width and Height for Single Stroke Gothic Letters (Uppercase) & Numbers
- 27. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 21 Fig. 3.4 Order of Strokes for Single Stroke Gothic Letters (Lowercase) Fig. 3.5 Order of Strokes for Single Stroke Gothic Italic Letters (Uppercase)
- 28. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 22 3.7 Spacing of Letters Uniformity in spacing of letters is a matter of equalizing spaces by eye. The background area between letters, not the distance between them, should be approximately equal. Some combinations, such as LT and VA, may even have to be slightly overlapped to secure good spacing. In some cases the width of a letter may be decreased. For example, the lower stroke of the L may be shortened when followed by A. Words are spaced well apart, but letters with in words should be spaced closely. Make each word a compact unit well separated from the adjacent words. For either upper case or lower-case lettering, make the spaces between words approximately equal to a capital O. Avoid spacing letters too far apart and words too close together. 3.8 Lettering in Maps Letters are generally used on maps as follows: Vertical capital: name of states, countries, towns, capitals, titles of the map etc. Vertical lower case: name of small towns, villages, post offices etc. Inclined capital: name of oceans, bays, gulfs, large lakes, rivers etc. Inclined lower case: name of rivers, creeks, small lakes, ponds, marshes and springs 3.9 Summary of ISO rules for Lettering 1. Most of the lettering is done in single stroke either in vertical or in inclined manner. 2. Only one style of lettering should be used throughout the drawing. 3. Lettering can be done either in free hand or using templates. 4. Proportion of Height & width a. For A,M,O,Q,T,V,X and Y, Height = Width. b. For W, height<Width.. c. For Other latters, Height>Width. d. For all numbers Height>Width 5. Line thickness of lower & upper case letters are made same as well as uniform. 6. Distance between adjacent lines or space between letters or numbers ≥ 2 × ℎ 7. If thickness of 2 adjacent line is different, spacing = 2 × ℎ ℎ 8. Standard height of letters and numbers are 2.5,3.5,5.0,7.0,10.0,14.0 and 20.0 mm 9. Height of letter or number≥ 2.5 10. When both capital and lower-case letters are to be combined, if c=2.5mm then h will be 3.5mm.
- 29. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 23 ISO 3098-2:2000 specification for relative dimensions of characters and spacing is illustrated here: Table 3.1 Lettering A (d=h/14): Characteristics Ratio Dimension Height of capitals, h (14/14)h 2.5 3.5 5 7 10 14 20 Height of lower-case letters, c (without step or tail) (10/14)h - 2.5 3.5 5 7 10 14 Spacing between characters, a (2/14)h 0.35 0.5 0.7 1 1.4 2 2.8 Minimum spacing of base line, b (20/14)h 3.5 5 7 10 14 20 28 Minimum spacing between words, e (6/14)h 1.05 1.5 2.1 3 4.2 6 8.4 Thickness of line, d (1/14)h 0.18 0.25 0.35 0.5 0.7 1 1.4 Table 3.2 Lettering B (d=h/14): Characteristics Ratio Dimension Height of capitals, h (10/10)h 2.5 3.5 5 7 10 14 20 Height of lower-case letters, c (without step or tail) (7/10)h - 2.5 3.5 5 7 10 14 Spacing between characters, a (2/10)h 0.5 0.7 1 1.4 2 2.8 4 Minimum spacing of base line, b (14/10)h 3.5 5 7 10 14 20 28 Minimum spacing between words, e (6/10)h 1.5 2.1 3 4.2 6 8.4 12 Thickness of line, d (1/10)h 0.25 0.35 0.5 0.7 1 1.4 2 Fig. 3.6 Relative Dimensions of Letters and Numbers (ISO guideline)
- 30. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 24 Exercise and Assignments 1. Following ISO guidelines complete lettering of all the uppercase letters and numbers in “Single Stroke Gothic-Vertical” style. 2. Following ISO guidelines complete lettering of all the uppercase letters and numbers in “Single Stroke Gothic-Italic” style. 3. Following ISO guidelines complete lettering of all the lowercase letters in “Single Stroke Gothic- Vertical/Italic” style. Review Questions: 1. Why have you studied lettering? 2. What is the difference between Gothic and Roman letters? 3. Write the letter “A”/ “a”/“T” in Gothic, Roman, Italic and Text style. 4. Which style of lettering is most commonly used in engineering drawing and why? 5. What do you mean by guidelines? Why is it used? 6. How guidelines are drawn for uppercase/lowercase letters? 7. What are the ISO rules for lettering? 8. How do you maintain the spaces between letters, words and lines? 9. Which letters have equal height and width? 10. Which letters have height>width and which one have width>height? 11. What are the standard heights of letters in engineering drawing? 12. Write a word/your name/Course code in single stroke gothic letters.
- 31. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 25 CHAPTER 4 GEOMETRIC CONSTRUCTION Objectives Objectives of studying geometric figures are: To learn to define geometric nomenclatures like angles, lines etc. To improve expertise in using drawing instruments. To learn the steps to construct different geometric figures like lines, arcs, polygon, ellipse etc. in convenient way. 4.1 Introduction To be truly proficient in the layout of both simple and complex drawings, the drafter must know and fully understand the many geometric construction methods used. These methods are illustrated in this chapter, and are basically simple principles of pure geometry. These simple principles are used to actually develop a drawing with complete accuracy, and in the fastest time possible, without wasted motion or any guesswork. Applying these geometric construction principles give drawings a finished, professional appearance. Strict interpretation of geometric construction allows use of only the compass and an instrument for drawing straight lines but in technical drawing, the principles of geometry are employed constantly, but instruments are not limited to the basic two as T-squares, triangles, scales, curves etc. are used to make constructions with speed and accuracy. Since there is continual application of geometric principles, the methods given in this chapter should be mastered thoroughly. It is assumed that students using this book understand the elements of plane geometry and will be able to apply their knowledge. 4.2 Geometric Nomenclature 4.2.1 Points in Space A point is an exact location in space or on a drawing surface. It is actually represented on the drawing by a crisscross at its exact location. 4.2.2 Lines Lines are straight elements that have no width, but are infinite in length (magnitude), and they can be located by two points which are not on the same spot but fall along the line. Lines may be straight lines or curved lines. A straight line is the shortest distance between two points. 4.2.3 Angle An angle is formed by the intersection of two lines. There are three major kinds of angles: right angels, acute angles and obtuse angles. Fig. 4.1 Points and Lines
- 32. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 26 4.2.4 Triangles A triangle is a closed plane figure with three straight sides and their interior angles sum up exactly 1800 . The various kinds of triangles: a right triangle, an equilateral triangle, an isosceles triangle, and an obtuse angled triangle. 4.2.5 Quadrilateral It is a plane figure bounded by four straight sides. When opposite sides are parallel, the quadrilateral is also considered to be a parallelogram. 4.2.6 Polygon A polygon is a closed plane figure with three or more straight sides. The most important of these polygons as they relate to drafting are probably the triangle with three sides, square with four sides, the hexagon with six sides, and the octagon with eight sides. A polygon is said to be “Regular Polygon” when all of its sides are equal in length and each of the internal angles formed at corners are equal in magnitude. Some helpful relations to be remembered for regular polygons are: 1. = ( ) ; ℎ , = . . 2. , = ; ℎ , = ℎ ℎ = . . 3. . = ( ) Fig. 4.2 Triangles Fig. 4.3 Quadrilaterals Fig. 4.4 Polygons
- 33. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 27 4.2.7 Circle A circle is a closed curve with all points on the circle at the same distance from the center point. The major components of a circle are the diameter, the radius and circumference. 4.2.8 Solids They are geometric figures bounded by plane surfaces. The surfaces are called faces, and if these are equal regular polygons, the solids are regular polyhedral. 4.3 Techniques of Geometric constructions To construct the above mentioned geometric figures, we have to know some principles and procedures of geometric construction. Thus, the remaining of this chapter is devoted to illustrate step-by-step geometric construction procedures used by drafters and technicians to develop various geometric forms. First of all we have to be well-expertise in using set squares particularly for drawing parallel and perpendicular lines. Fig. 4.7 illustrates it. Fig. 4.5 Circles Fig. 4.6 Solids Fig. 4.7 Use of Set-Square for Making Parallel and Perpendicular Lines
- 34. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 28 4.3.1 How to Bisect a Line or an Arc To bisect a line means to divide it in half or to find its center point. In the given process, a line will also be constructed at the exact center point at exactly 900 . Given: Line A-B Step 1: Set the compass approximately two-thirds of the length of line A-B and swing an arc from point A. Step 2: Using the exact same compass setting, swing an arc from point B. Step 3: At the two intersections of these arcs, locate points D and E Step 4: Draw a straight-line connecting point D with point E. Where this line intersects line A-B, it bisects line A-B. Line D-E is also perpendicular to line A-B at the exact center point. 4.3.2 How to Divide a Line into a Number of Equal Parts Given: Line A-B Step 1: Draw a construction line AC that starts at end A of given line AB. This new line is longer than the given line and makes an angle preferably of not more than 300 with it. Step 2: Find a scale that will approximately divide the line AB in to the number of parts needed (5 in the example below), and mark these divisions on the line AC. There are now ‘n’ equal divisions from A to D that lie on the line AC (5 in this example). Step 3: Set the adjustable triangle to draw a construction line from point D to point B. Then draw construction lines through each of the remaining ‘n-1’ divisions parallel to the first line BD by sliding the triangle along the straight edge. The original line AB will now be accurately divided. C D Fig. 4.9 Dividing a Line into 7 Equal Parts Fig. 4.8 Bisecting an Arc or a Line
- 35. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 29 4.3.3 How to Bisect an Angle To bisect an angle means to divide it in half or to cut it in to two equal angles. Given: Angle BAC Step 1: Set the compass at any convenient radius and swing an arc from point A Step 2: Locate points E and F on the legs of the angle, and swing two arcs of the same identical length from points E and F, respectively. Step 3: Where these arcs intersect, locate point D. Draw a straight line from A to D.This line will bisect angle BAC and establish two equal angles: CAD and BAD. 4.3.4 How to Draw an Arc or Circle (Radius) through Three Given Points Given: Three points in space at random: A, B and C. Step 1: With straight line, lightly connect points A to B, and B to C, Step 2: Using the method outlined for bisecting a line, bisect lines A-B and B-C Step 3: Locate point X where the two extended bisectors meet. Point X is the exact center of the arc or circle. Step 4: Place the point of the compass on point X and adjust the lead to any of the points A, B, or C (they are the same distance), and swing the circle. If all work is done correctly, the arc or circle should pass through each point. Fig. 4.11 Drawing of Arc Through 3 Points Fig. 4.10 Bisecting an Angle
- 36. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 30 4.3.5 How to Transfer an Odd Shape (Triangular) Given: Triangle ABC. Step 1: Letter or number the various corners and point locations of the odd shape in counterclockwise order around its perimeter. In this example, place the compass point at point A of the original shape and extend the lead to point B. Swing a light arc at the new desired location. Letter the center point as A' and add letter B' at any convenient location on the arc. It is a good habit to lightly letter each point as you proceed. Step 2. Place the compass point at letter B of the original shape and extend the compass lead to letter C of the original shape. Step 3. Transfer this distance, B-C, to the layout. Steps 4 and 5. Going back to the original object, place the compass point at letter A and extend the compass lead to letter C. Transfer the distance A-C as illustrated in Figure. Locate and letter each point. Step 6. Connect points A', B', and C’ with light, straight lines. This completes the transfer of the object. Recheck all work and, if correct, darken lines to the correct line weight. 4.3.6 How to Transfer Complex Shapes A complex shape can be transferred in exactly the same way by reducing the shape into simple triangles and transferring each triangle using the foregoing method. Given: An odd shape, A, B, C, D, E, F, G. Step 1: Letter or number the various corners and point locations of the odd shape in clockwise order around the perimeter. Use the longest line or any convenient line as a starting point. Line A-B is chosen here as the example. Lightly divide the shape into triangle divisions, using the baseline if possible. Transfer each triangle in the manner described in previous procedure. Suggested triangles to be used in example are ABC, ABD, ABE, ABF and ABG. Step 2: This completes the transfer. Check all work and, if correct, darken in lines to correct line thickness. Fig. 4.12 Transferring a Triangle to Another Location
- 37. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 31 4.3.7 How to Draw A Pentagon (5 Sides) Given: The locations of the pentagon center and the diameter of circle that will circumscribe the pentagon. Step 1: Draw the circle with given diameter taking given location as center (C). Letter a diameter as HB. Step 2: Draw a perpendicular CD that meets the circumference at D. Step 3: Bisect radius CB at A. Step 4: With A as center, and CD as radius, strike arc DE that meets the radius CH at E. Step 5: With D as center, and DE as radius, strike arc EF that meets the nearest circumference at F. Step 6: Draw line DF, this is the length of one side. Now set off distances DE around the circumference of the circle, and draw the sides through these points. 4.3.8 How to Draw a Hexagon (6 Sides) Given: The locations of the hexagon center and the diameter of circle that will circumscribe the hexagon. Step 1: Draw the circle with given diameter taking given location as center. Step 2: Extend the compass upto a length equal to the radius of the ciecle. Step 3: Starting from any point, say A1, on the circumference, cut 6 equal segments and mark the points as A1, A2, A3, A4, A5 and A6. Step 4: Join each 2 consecutive points to obtain the hexagon A1 A2 A3 A4 A5A6. 4.3.9 How to Draw an Octagon (8 Sides) Given: The locations of the octagon center and the diameter of circle that will be inscribed by the octagon. Step 1: Draw the circle with given diameter taking given location as center. Step 2: Draw any two mutually perpendicular diameters. Step 3: Draw tangents to the circle at the ends of diameters to obtain a square. Step 4: Draw diagonals of the square. Diagonals will intersect the circle at 4 points. Step 5: Draw tangent to the circle at the 4 intersection points obtained in step 4. These tangents will meet the sides of square drawn in step 3. Now darken the obtained octagon. Fig. 4.13 Transferring a Complex Shape to Another Location Fig. 4.15 Drawing of a HexagonFig. 4.14 Drawing of a Pentagon Given Shape Step 1 Step 2
- 38. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 32 4.3.10 How to Draw any Sided Regular Polygon i. Given: Number of sides and the diameter of circle that will circumscribe the polygon. Step 1: Draw the circle with given diameter taking given location as center. Mark a diameter. As example let us draw a 7 sided polygon. Mark the diameter as 0-7. Step 2: Divide the diameter in “n” equal segments using parallel line method. Here n=7 for our case. Step 3: Construct an equilateral triangle (0-7-8) with the diameter (0-7) as one of its sides. Step 4: Draw a line from the apex (point 8) through the second point on the line (point 2) and extend line 8-2 until it intersects the circle at point 9. Step 5: Now 0-9 is the length of each side of the polygon. Taking 0-9 as radius of compass, cut the circumference in 7 equal segments to obtain the corners of the seven sided polygon and connect the points. ii. Given: Length of one side and number of sides (i.e. 5 for pentagon, 6 for hexagon, 8 for octagon etc.) Step 1: Calculate one internal angle of the polygon using formula ( ) ; Step 2: Draw a line of length equal to the given side. Step 3: Draw the obtained internal angle at one end of the line and set off distances equal to the given side. Step 4: Continue repeating the step 3 until you reach another end of 1st line. Thus the polygon will be drawn. iii. Given: Number of sides and diameter of out scribing circle. Step 1: Draw the circle. Using protractor, Draw an angle equal to ° at the center of circle where n = number of sides. Step 2: The lines drawn for the angle cuts the circle at A and B. Then AB is the length of one side. Now set off distances AB around the circumference of the circle, and draw the sides through these points. iv. Given: Number of sides and diameter of inscribing circle. Step 1: Draw the circle. Using protractor, Divide the central 3600 angle into “n” number of equal part by drawing “n” number of angles each equal to ° at the center of circle where n = number of sides. Step 2: The lines drawn for the angles cuts the circle at A, B, C, D…. etc. At each point of intersection draw a tangent to the circle. The tangents will meet each other at 1, 2, 3, 4…… etc. Then 1-2-3-4-….. is the required polygon. Fig. 4.16 Drawing of an Octagon
- 39. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 33 4.3.11 How to Locate the Center of a Given Circle Given: A circle without a center point. Step 1: Using the T-square, draw a horizontal line across the circle approximately halfway between the estimated center of the given circle and the uppermost point on the circumference. Label the end points of the chord thus formed as A and B. Step 2: Draw perpendicular lines (90°) downward from points A and B. Locate points C and D where these two lines pass through the circle. Step 3: Carefully draw a straight line from point A to point D and from point C to point B. Where these lines cross is the exact center of the given circle. Place a compass point on the center point; adjust the lead to the edge of the circle and swing an arc to check that the center is accurate. Fig. 4.17 Drawing of Any Sided Polygon Fig. 4.18 Locating the Center of Given Circle (i) (ii) (iii) (iv)
- 40. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 34 4.3.12 How to Draw Arc Tangent to a Straight Line and a Curve Given: Straight line AB, an arc with a center point O or radius r, and a required radius (R) of arc tangent. Step 1: Take a radius equal to + , place the needle of compass at the center of given curve and draw an arc EF. Step 2: Draw a line CD parallel to AB at a distance so that the line CD and arc EF intersects at point G. Step 3: Taking G as center and R as radius draw an arc. This arc will touch the line AB and the given arc. 4.3.13 How to Draw Arc Tangent to Two Arcs of Different Radius Given: Two arcs AB, CD with their center point O1 and O2 or radius r1 and r2, and a required radius (R) of arc tangent. Step 1: If radius of arcs are not given but their center location is known, say O1 and O2 ; Take any point P on the 1st arc and taking it as center draw an arc EF with radius R. Join O1P and extend it until it meets the curve EF at Q. Take O1 as center and O1Q as radius draw another arc QS. If the radius of arcs are given then simply take O1 as center and draw the arc QS by taking radius equal to r1+R. Step 2: Following similar method as in step 1, draw another arc TS taking O2 (Center of 2nd arc) as center such that TS intersects QS at S. Step 3: Take S as center and R as radius, draw an arc that will touch the given 2 arcs. Fig. 4.19 Drawing of Arc Tangent to a Straight Line and Curve Fig. 4.20 Drawing of Arc Tangent to 2 Arcs Center locations given Radius given
- 41. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 35 4.3.14 How to Draw an Ogee Curve An ogee curve is used to join two parallel lines. It forms a gentle curve that reverses itself in a neat symmetrical geometric form. Given: Parallel lines A-B and C-D. Step 1: Draw a straight line connecting the space between the parallel lines. In this example, from point B to point C. Step 2: Make a perpendicular bisector to line B-C to establish point X. Step 3: Make perpendicular bisectors to the lines B-X and X-C. Step 4: Draw a perpendicular from line A-B at point B to intersect the perpendicular bisector of B-X, which locates the first required swing center. Draw a perpendicular from line C-D at point C to intersect the perpendicular bisector of C-X which locates the second required swing center. Step 5: Place the compass point on the first swing point and adjust the compass lead to point B, and swing an arc from B to X. Place the compass point on the second swing point and swing an arc from X to C. This completes the ogee curve. Note: point X is the tangent point between arcs. Check and. if correct, darken in all work. Step-1 Step-2 Step-3 Step-4 Step-5 Fig. 4.21 Drawing of an Ogee Curve
- 42. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 36 4.3.15 How to Draw Straight Tangent to Two Arcs of Different Radius Given: Two arcs of different radius and their center location A and B or radius r1 , r2 and center distance AB. Step 1: Consider the two given circles with centers A and B respectively. If r1 , r2 and AB are given draw them accordingly. Step 2: Draw any radius of the curve having larger diameter, BC, in example. Cut BD=radius of curve with smaller diameter. Taking center as B and radius as CD draw an arc EF. If value of r1 , r2 are given simply draw the arc EF taking radius as r2- r1 and center as B. Step 3: Using set square draw a tangent AF to the arc EF from point A. Step 4: Join BF and extend it until it meets the given curve at P. Step 5: Complete the rectangle AFPQ. Then PQ will be the required tangent. 4.3.16 How to Draw an Ellipse (Four-centered Approximate Method) Given: Major and Minor axis length (say, a and b respectively). Step 1: Draw a line PQ=a and find out its mid-point O. At O draw a perpendiculars OR=OS=b/2. Step 2: Taking center O and radius OP, draw an arc PA that intersects the extended minor axis (RS) at A. Step 3: Join PR. Taking R as center and RA as radius draw an arc that intersects PR at B. Step 4: Bisect PB at C and draw a perpendicular at C that intersects the extended minor axis (RS) at D. The line CD also intersects PO at E. Step 5: Draw OE’ equal to OE and OD’ equal to OD. Join DE’, D’E and D’E’ and extend them. Step 6: Taking D and D’ as centers and DR or D’S as radius draw 2 arcs MRN and KSL respectively. Step 7: Taking E and E’ as centers and PE or QE’ as radius draw another 2 arcs KPM and NQL respectively. Thus the ellipse will be completed. Fig. 4.23 Drawing of an Ellipse Fig. 4.22 Drawing of a Common Tangent to 2 Curves
- 43. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 37 Exercise and Assignments 1. Divide a line of length 40mm into 7 equal parts. 2. Draw a circle touching three points A, B and C with coordinates A(0,0), B(0,20) and C(15,0). 3. Draw a regular pentagon inscribing a circle of diameter 80mm. Avoid use of protractor. 4. Draw a regular pentagon out scribing a circle of diameter 100mm. 5. Draw a regular pentagon having length of side as 45mm. 6. Draw a regular hexagon inscribing a circle of diameter 80mm. Avoid use of protractor. 7. Draw a regular hexagon out scribing a circle of diameter 100mm. 8. Draw a regular hexagon having length of side as 45mm. 9. Draw a regular octagon inscribing a circle of diameter 80mm. Avoid use of protractor. 10. Draw a regular octagon out scribing a circle of diameter 100mm. Avoid use of protractor. 11. Draw a regular octagon having length of side as 45mm. 12. Draw a 9 sided regular polygon inscribing a circle of radius 50mm. 13. A 80mm long horizontal straight line is located outside a circle of radius 30mm, such that a 50mm line drawn from center of the circle meets the mid-point of the straight line at right angle. Draw two arc tangents, each having a radius of 40mm touching the circle and one of the ends of the straight line. 14. Draw a common arc tangent of radius 70mm to the two circles having their centers 80mm apart and having diameters of 50mm and 30mm respectively. 15. Draw an ogee curve to connect two parallel lines each of length 20mm and their mid-points spaced 30mm vertically and 70mm horizontally. 16. Two wheels with diameters 3.5m and 2m are required to be provided with a belt. Draw the line diagram of the arrangement. Use a reduced scale. 17. Draw an ellipse having major and minor axis length as 90mm and 60mm. Review Questions 1. Why have you studied geometric drawings? 2. Name the geometric nomenclatures and draw a qualitative shape of them. 3. Name and draw the different types of lines. 4. What do you mean by isosceles, equilateral and scalene triangle? 5. What are different types of quadrilaterals? Draw them. 6. What is the difference between parallelogram, trapezoid, rectangle, square and rhombus? 7. What is name of a 5/6/7/8/9/10/11/12 sided polygon? 8. What do you mean by regular polygon? 9. How can you calculate summation of all internal angles of a polygon? 10. Calculate one internal angle of a 5/7/9/11 sided regular polygon. 11. How can you calculate the length of one side of a regular polygon from the radius/diameter of the circle that circumscribes it? 12. A circle has a diameter of 100cm. What will be the length of side of a 5/7/9/11 sided regular polygon drawn inscribing the circle? 13. How many diagonals are possible for a 5/7/9/11 sided polygon? 14. Draw a circle showing chord, diameter, radius, arc, segment and sector. 15. Name some solid geometric form. 16. What is the solid form of a square/circle/triangle? 17. Draw a parallel or perpendicular line to a given line at any point using set-square. 18. Divide a given line into 3/5/9 parts. 19. Find the half, 1/4th , 1/8th of a given angle without protractor. 20. Transfer a given polygon to other specified point. 21. Locate the center of a given circle. 22. Draw a tangent to the two given circle.
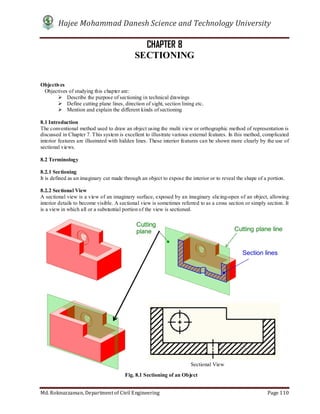
- 44. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 38 CHAPTER 5 DIMENSIONING Objectives Objectives of studying dimensioning are: To know the purposes of dimensioning To understand the differences between dimension line, extension line, leaders etc. To know the guidelines of dimension system. To learn to draw the dimension of technical drawings as per the standard 5.1 Purpose of Dimensioning The purpose of dimensioning is to provide a clear and complete description of an object. A complete set of dimensions will permit only one interpretation needed to construct the part. In some cases, engineering drawing becomes meaningless without dimensioning. Maintaining scale only does not make a drawing sufficient for manufacturer. By direct measurement from drawing according to the scale is very laborious, time-consuming and such a part cannot be manufactured accurately. In general dimensioning system provides following information Sizes and locations of features Material’s type Number required Kind of surface finish Manufacturing process Size and geometric tolerance 5.2 General Conditions for Dimensioning Accuracy: correct values must be given. Clearness: dimensions must be placed in appropriate positions. Completeness: nothing must be left out, and nothing duplicated. Readability: the appropriate line quality must be used for legibility. 5.3 Elements of Dimension System Extension lines Dimension lines Arrowheads Leaders Texts, numbers and symbols. 5.4 Rules for Dimensioning 5.4.1 General Rules for Dimensioning Dimensioning should be given within the extent of the view in general. Dimensioning should not be duplicated in other view. No subtraction or addition should be required to define or locate a feature. Dimensioning should be inserted on relatively larger available view to make it clear. One system of dimensions either unidirectional or aligned has to be used throughout the drawing. Dimensioning to the hidden lines should be avoided, in general. Dimensioning should be made on the view, which represents the shape of the part best. A zero must be placed before decimal point. Fig. 5.1 Dimensioning Elements
- 45. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 39 5.4.2 Rules of Extension Lines Extension lines are the lines that indicate the point or line or space on the drawing to which dimension is being applied. Following conditions should be maintained while inserting an extension line: A gap of 1mm has to be kept between extension line and visible line. An extension line should be extended about 3mm from the outmost dimension line. Extension lines may cross each other without break. Center lines can be used as extension lines. Extension lines are drawn usually perpendicular to dimension lines. But for overcrowded drawing they can be drawn at an oblique angle as well. 5.4.3 Rules of Dimension Lines Dimension lines are the lines that show the dimensions of a specific portion indicated by extension lines. Following conditions should be maintained while inserting a dimension line: Dimension line should be approximately 10mm away from visible line. Spacing between consecutive parallel dimension lines may also be kept as 10mm. Dimension lines are broken near the middle to allow space for dimensions. As far as possible dimension lines should be placed outside the view. Dimension lines should not cross each other. Center lines should never be used as dimension lines. If space between extension lines is very short for inserting arrows, the arrows may be provided outside the extension lines. 5.4.4 Rules of Arrowhead Arrowheads are used at both ends of dimension lines and at the ends of leaders. They are usually drawn freehand. Following conditions should be maintained while inserting an arrowhead: As far as possible all arrowheads should be identical in shape and size throughout the drawing. An approximate ratio of the length to width of arrowhead as 3:1 should be maintained. Arrowheads must touch the line. It must not be either away from the line or cross the line. Fig. 5.2 Extension Lines in Proper Way Correct Wrong Fig. 5.3 Dimension and Extension lines Fig. 5.4 Arrowhead
- 46. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 40 5.4.5 Rules of Leaders Leaders are used in engineering drawing for dimensioning of arcs, circles etc. They are also used to present note, symbols, item number or part number etc. Following conditions should be maintained while inserting a leader: A leader should always be inclined at an angle of 600 preferably and 450 occasionally. The length of horizontal bar should be 3mm. A leader should be terminated by either an arrowhead or a small dot of about 1.5mm diameter. Leaders should not be drawn bent unless necessary. Leaders should not cross each other, however, they may be drawn parallel to each other with a common horizontal bar. To direct a circle or an arc the leader should be so drawn, if it is imagined to extend it must pass through the center of the circle or the arc. All notes, symbols and dimensions in a leader need to be provided in horizontal direction. 5.5 Direction of Dimensions Direction of dimensions is chosen in either of the two systems: A. Unidirectional system: All the dimensions are oriented to be read from the bottom of drawing. It is also known as horizontal system. This system is preferred to aligned system. B. Aligned system: All the dimensions are oriented to be read from the bottom or right side of the drawing. Fig. 5.5 Leaders Fig. 5.6 Unidirectional System Fig. 5.7 Aligned System
- 47. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 41 5.6 Technique of Dimensioning There are two basic steps in dimensioning objects, regardless of the type of object. Step 1: Apply the size dimensions. These are dimensions which indicate the overall size of the object and the various features which make up the object. Step 2: Apply the locational dimensions. Locational dimensions are dimensions which locate various features of an object from some specified datum or surface. Figure 9-29 gives examples of size and location dimensions. 5.7 Dimensioning in Limited Space If space between the extension lines is too small to insert the dimension digits, they may be provided al left or right side of extension lines. Sometimes the space may be even too small to insert arrows, in such case dimensions as well as arrows can be provided on outside of the extension lines as shown in Fig. 5.9. If the space is very limited for inserting dimension lines, the portion to be dimensioned are enlarged for clear dimensioning. Sometimes smaller circular dots are used in place of arrowhead for space limitation. Fig. 5.10 shows such example. Fig. 5.10 Dimensioning in Limited Space Portion to be enlarged Enlarged view of A Use of small dot Fig. 5.8 Size and Location Dimension Fig. 5.9 Dimensioning in Limited Space
- 48. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 42 5.8 Dimensioning of Angles Angles are normally written in degrees, minutes, and seconds. The symbols used to depict degrees, minutes, and seconds are also shown in this figure. Angular measurements may also be stated in decimal form. This is particularly advantageous when they must be entered into an electronic digital calculator. The key to converting angular measurements to decimal form is in knowing that each degree contains 60 minutes, and each minute contains 60 seconds. Fig. 5.11 Dimensioning of Angles
- 49. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 43 5.9 Dimensioning of Arcs The dimension figure and the arrowhead should be inside the arc, where there is sufficient space. If space is limited then leaders can be used comfortably. 5.10 Dimensioning of Chord Length, Arc Length and Angle Chords, arcs, and angles are dimensioned in a similar manner. The difference is: When dimensioning a chord length, the dimension line should be perpendicular and the extension lines parallel to the chord. When dimensioning an arc length, the dimension line runs concurrent with the arc curve, but the extension lines are either vertical or horizontal. An arc symbol is placed above the dimension. When dimensioning an angle, the extension lines extend from the sides forming the angle, and the dimension line forms an arc. Fig. 5.12 Dimensioning of Arc Fig. 5.13 Difference among the Dimensioning Of Chord Length, Arc Length and Angle
- 50. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 44 5.11 Dimensioning of Round Holes Round holes are dimensioned in the view in which they appear as circles. Smaller holes may be dimensioned using a leader which points toward the center of the hole in which the note gives the diameter, or extension lines may be drawn from the circle with a dimension that also indicates the diameter. Larger circles are dimensioned with a dimension line drawn across the circle through its center at an angle with the diameter dimension shown. It is important when dimensioning holes to call off the diameter, not the radius. 5.12 Dimensioning of Blind Holes It is usual practice to use leader line and local note to specify diameter and hole’s depth in the circular view. 5.13 Dimensioning of Chamfer It is usual practice to use leader line and note to indicate linear distance and angle of the chamfer. Fig. 5.14 Dimensioning of Circular Holes Fig. 5.15 Dimensioning of Blind Holes Fig. 5.16 Dimensioning of a Chamfer
- 51. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 45 5.14 Common Mistakes in Dimensioning Wrong Wrong Wrong Correct Correct Correct A B C Fig. 5.17 Common Mistakes in Dimensioning (Contd.)
- 52. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 46 Fig. 5.17 Common Mistakes in Dimensioning (Contd.) Wrong Correct Wrong Correct Wrong Correct F E D
- 53. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 47 Wrong Correct H Correct Wrong G Fig. 5.17 Common Mistakes in Dimensioning (Contd.) I
- 54. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 48 5.15 Worked-out Examples of Dimensioning (A) (B) (C) (D) (E)
- 55. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 49 (F) (H) (I) (J)
- 56. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 50 (K) (L) (M) (N) (O) (P)
- 57. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 51 Exercise and Assignments: Complete Dimensioning of the figures below: (5) (4) (1) (2) (6) (3)
- 58. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 52 (7) (8) (9) (10) (11) (12)
- 59. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 53 Review Questions 1. Why have you studied dimensioning? 2. Which information are provided in dimensioning system? 3. What are the conditions for a good dimension system? 4. Name the elements of dimensioning system. 5. What are the rules that must be followed while dimensioning? 6. What is the purpose of extension line and what are the rules to be followed for extension line? 7. What is the purpose of dimension line and what are the rules to be followed for dimension line? 8. What is the purpose of leaders and what are the rules to be followed for leaders? 9. What are the uses of arrowheads in dimensioning and what are the rules to be followed for arrowheads? 10. What is the proportion of width and length of an arrowhead? 11. Draw a square out scribing a circle and complete dimensioning. 12. What is the difference between aligned and unidirectional dimensioning? Give examples. 13. What will you do when the space between extension lines is too small to accommodate the dimension line with text at its middle? 14. What will you do when the space between extension lines is too small to accommodate the dimension line with arrows? 15. What will you do when the feature is too small to make the dimension visible? 16. What are the different ways to show dimension of an arc/circle? 17. What is the difference of dimensioning of chord, arc and angle? Give example. 18. Draw a circular hole of 2cm deep and give dimensions to it.
- 60. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 54 CHAPTER 6 SCALES Objectives Objectives of studying this chapter are: To learn to construct different types of scale. To learn to produce an enlarged or reduced drawing. To learn to make measurements using scales drawn in maps or drawings. 6.1 Scale The proportion by which we either reduce or increase the actual size of the object on a drawing is known as scale. It is not possible always to make drawings of an object to its actual size as the extent of drawing paper is limited and also sometimes the objects are too small to make it clearly understandable by drawing its actual size in drawing paper. Scale is the technique by which one can represent an object comfortably as well as precisely within the extent of drawing paper. In other words, a scale is a measuring stick, graduated with different divisions to represent the corresponding actual distance according to some proportion. Numerically scales indicate the relation between the dimensions on drawing and actual dimensions of the objects. 6.2 Uses of scale To prepare reduced or enlarged size drawings. To set off dimensions. To measure distances directly. 6.3 Sizes of Scales Full size scale Reducing scale Enlarging scale Full Size Scale The scale in which the actual measurements of the object are drawn to the same size on the drawing is known as full size scale. It is represented as 1:1 scale. If possible, drawing should be done in full scale. Reducing Scale The scale in which the actual measurements of the object are reduced to some proportion is known as reducing scale. The standard formats of reducing proportions are: 1:2 - drawing made to one-half of the actual size 1:5 - drawing made to one-fifth of the actual size 1:10 - drawing made to one-tenth of the actual size 1:50 - drawing made to one-fiftieth of the actual size 1:100 - drawing made to one-hundredth of the actual size Enlarging Scale The scale in which the actual measurements of the object are increased to some proportion is known as reducing scale. The standard formats of enlarging proportions are: 2:1 - drawing made to twice the actual size 5:1 - drawing made to five times the actual size 10: - drawing made to ten times the actual size
- 61. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 55 6.4 Classification of Scales Plain Scales Diagonal Scales Comparative Scales Vernier Scales Chord Scales The first two type (plain and diagonal) of scales are usually used in engineering drawings. 6.4.1 Plain Scale The scale that can measure one main unit and one sub-unit of the main unit or up to a fraction of 1st decimal point of the main unit is known to be a plain scale. It is simply a line divided into a number of equal parts and the 1st part is further sub-divided into small parts. Kilometers and Hectometers, Meters and Decimeters, Meters and 1/10th of Meters etc. can be measured using plain scales. 6.4.2 Diagonal Scale The scale that can measure one main unit and two sub-units of the main unit or up to a fraction of 2nd decimal point of the main unit is known to be a diagonal scale. It is so named because the 2nd sub-unit or 2nd decimal of main unit is obtained by the principle of diagonal division. Kilometers-Hectometers-Decameters, Decameters-Meters-Decimeters, Meters-1/10th of Meters- 1/100th of Meters etc. can be measured using diagonal scales. Table 6.1 Difference between Plain Scale and Diagonal Scale 6.4.3 Comparative Scale When the given scale of a plan reads a certain measure and it is required to construct a new scale for the same plan to read in some other measures, the new scale is called comparative scale or corresponding scale. For example let us consider a plan drawn in inch units and scale provided with drawing can measure in feet and inch. If we draw another scale taking same R.F. that can measure in feet, inch and 1/8th of inch it will be a comparative scale. Also if we draw another scale that can measure in cm and mm with same R.F. it will also be a comparative scale. 6.4.4 Vernier Scale It is device for measuring fractional parts of the smallest division of the main scale. It consists of a fixed main scale and a movable vernier scale. The vernier part is graduated in “n” number of divisions in such a way that it coincides with “n-1” number of smallest divisions of main scale. 6.4.5 Chord Scale The scale which is used to make or to measure angles of any magnitude is known as chord scale. This scale is usually marked on a rectangular protractor. 6.5 Necessity of Construction of Scale on Drawing In most of the cases the distances in a drawing is found to be different than the corresponding actual distance. Therefore, to get the actual measurements, it is a must to know the proportion using which the drawing is prepared. Sometimes the drawing may need to be prepared to an odd proportion (like 1:2.7 or 13.2:1) for which a physical scale is not available. In such case individual scale construction is required for that specific drawing. It is often found helpful and convenient to construct and draw the corresponding scale on the drawing than mentioning the proportion in language. On the other hand if a drawing is to be used after decades, the paper may shrink or Plain Scale Diagonal Scale It can measure one main unit and one sub-units of the main unit It can measure one main unit and two sub-units of the main unit It can measure up to a fraction of 1st decimal point of the main unit. It can measure up to a fraction of 2nd decimal point of the main unit. Scale is constructed by simply dividing the line longitudinally. Scale is constructed by dividing the line longitudinally as well as vertically and diagonally.
- 62. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 56 expand by absorbing or leaving moisture due to temperature effect. Taking measurements from such a drawing using the proportion mentioned will give some inaccurate result. But if a scale is constructed an drawn during the preparation of 1st time, the drawn scale will also shrink or expand in the same proportion to the drawing. Thus if one take measurements with the help of the drawn scale, accurate measurements will be obtained. 6.6 Information Necessary for Construction of a Scale Following are the necessary information required for construction of a scale: The representative fraction (R.F.) of the scale. The unit or units to be presented. The maximum length to be measured. 6.6.1 The Representative Fraction (R.F.) or Scale Factor (S.F.) The ratio of the distance on drawing paper of an object to the corresponding actual distance of the object is known as the representative fraction (R.F.) or the scale factor (S.F.). It is to be remembered that for finding RF the distances used for calculation must be in same unit. And being a ratio of same units, R.F. itself has no unit. Mathematically, . . = [ ] 6.6.1.1 Worked out Examples of R.F. Calculation Example 6.1: In a certain map, 2.5 centimeters of measured length represents 5 hectometers of actual distance. Calculate R.F. for the scale of this map. Solution: Representative Fraction of the scale for this map, . . = . × × × × = 1: 20000 Example 6.2: To draw a microscopic element of a machine part, it is to be enlarged in drawing such a manner that one-fifth of one millimeter is to be represented by 1.5 meters. Find out RF of the scale for this drawing. Solution: Representative Fraction of the scale, . . = . × × × = 7500 7500: 1 Example 6.3: A scale is to be constructed for a drawing of a plot such that 100 square feet of area is to be represented by 1 square inch. What will be the R.F. of this scale? Solution: Here 1 sq. inch represents 100 sq.ft. or we can write 1 ℎ ≈ 100 Taking under root on both sides, we get 1 ℎ ≈ 100 ∴ 1 ℎ ≈ 10 , . .= 1 10 × 12 = 1 120 1: 120
- 63. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 57 6.6.2 Units of Measurement It is modern practice to use metric system of units in engineering drawing. However, sometimes British system is also used. It is important to have clear understanding about unit conversion in both system. Table 6.2 to Table 6.7 presents the units of measurements, their symbols and conversions. Table 6.2 Metric Units for Linear Measurement Table 6.4 Metric Units for Area Measurement Table 6.6 Metric Units for Volumetric Measurement 1000 cubic millimeters (mm3 ) = 1 cubic centimeter (cm3 ) 1000 cubic centimeters (cm3 ) = 1 cubic decimeter (dm3 ) 1000 cubic decimeters (dm3 ) = 1 cubic meter (m3 ) 6.7 Construction of Plain Scale Following are the steps for constructing a plain scale Find out the R.F., if not given directly. Find out the length of scale = . . × ℎ ℎ [Note: If length of object or maximum length to be measured is not mentioned in problem, for convenience, take the length of scale about 15 cm or 6 inches] Draw a straight line, preferably horizontal, of required length as found in previous step. Divide the line into a number of divisions relating to the length of object and maximum length to be measured such that one segment represents one major unit. Avoid fractions, consider the next integer value. For instance, if maximum length to be measured is 6.2 km, then number of divisions will be 7. Place mark 0 at the end of 1st main division (Remember, not at the starting point of 1st division) and mark the other divisions sequentially toward right as 1,2,3….. etc. Divide the 1st main division into a number of divisions such that each of these smallest division represents one sub-unit. For instance if the scale need to measure in feet and inches, number of minor divisions will be 12. On the other hand if the scale is to measure in centimeters and millimeters or in meters and 1/10th of meter number of divisions will be 10. Mark the sub-unit sequentially toward left as 1, 2, 3…… etc. or 0.1, 0.2, 0.3……. etc. If space is limited they can be marked after every 2 division like 0, 2,4,….. etc. Mention the R.F. of the scale below the figure. Mention the name of main unit and sub-unit either at below or at the respective ends of the scale. 12 inches = 1 foot 3 feet = 1 yard 220 yards = 1 furlong 8 furlong = 1 mile 10 millimeters (mm) = 1 centimeter (cm) 10 centimeters (cm) = 1 decimeter (dm) 10 decimeters (dm) = 1 meter (m) 10 meters (m) = 1 decameter (dam) 10 decameters (dam) = 1 hectometer (hm) 10 hectometers (hm) = 1 kilometer (km) 100 square millimeters (mm2 ) = 1 square centimeter (cm2 ) 100 square centimeters (cm2 ) = 1 square decimeter (dm2 ) 100 square decimeters (dm2 ) = 1 square meter (m2 ) 100 square meters (m2 ) = 1 acre (a) 100 acres (a) = 1 hectare 100 hectares = 1 square kilometer (km2 ) 144 square inches = 1 square foot 9 square feet = 1 square yard 4840 square yards = 1 acre 640 acres = 1 square mile 1728 cubic inches = 1 cubic foot 27 cubic feet = 1 cubic yard Table 6.3 British Units for Linear Measurement Table 6.5 British Units for Area Measurement Table 6.7 British Units for Volumetric Measurement
- 64. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 58 6.7.1 Worked-out Examples of Plain Scale Construction Example 6.4: Construct a plain scale to show kilometers and hectometers when 2.5 centimeters are equal to 1 kilometer and long enough to measure upto 5.7 kilometers. Find R.F. of the scale and indicate distances (i) 4 kilometers and 5 hectometers and (ii) 5.4 kilometers on the scale. Solution: . .= 2.5 1 × 10 × 10 × 10 × 10 × 10 = 1 40000 1: 40000 ℎ = . . × ℎ = × 6 = × 6 × 1000 × 100 = 15 [ To avoid fraction, maximum distance is take 6 km instead of 5.7 km ] Now a horizontal line 15 cm long is drawn and is divided into 6 equal parts. From left staring 0 at 2nd division major units are marked sequentially toward right as 0, 1, 2, 3, 4 and 5. The 1st division is further divided into 10 divisions and starting at 0 mark placed earlier the sub-divisions are marked after every 2 division as 2, 4, 6, 8 and 10 toward left. R.F. and unit names are mentioned accordingly. Thus the scale is constructed and the required distances are indicated.
- 65. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 59 Example 6.5: A rectangular plot of land of area 64 square mile is represented on a certain map by area of 1 square inch. Draw a plain scale to show units of 10 miles and single miles. Find R.F. and mark a distance of 63 mile on this scale. Solution: Given, 1 ℎ ≈ 16 1 ℎ ≈ 64 ∴ 1 ℎ ≈ 8 , . . = 1 8 × 1760 × 3 × 12 = 1 506880 1: 506880 Here maximum distance to be measured is not given, but we need to ensure the measuring a distance of 63 mile. Thus we have to construct the scale for 70 miles of maximum distance. ℎ = . . × ℎ = × 70 = × 70 × 1760 × 3 × 12 ℎ = 8.75 ℎ Now a horizontal line 8.75 inch long is drawn and is divided into 7 equal parts. From left staring 0 at 2nd division major units are marked sequentially toward right as 0, 10, 20, 30, 40, 50 and 60. The 1st division is further divided into 10 divisions and starting at 0 mark placed earlier the sub-divisions are marked after every 2 division as 2, 4, 6, 8 and 10 toward left. R.F. and unit names are mentioned accordingly. Thus the scale is constructed and the required distances are indicated.
- 66. Hajee Mohammad Danesh Science and Technology University Md. Roknuzzaman, Department of Civil Engineering Page 60 Example 6.6: A car is moving at a speed of 60 kmph. On a scale one centimeter represents one third of a kilometer. Construct the scale and show the distance travelled by the car in 3 minutes and 30 seconds. What is the R.F. of the scale? Solution: . . = 1 1 3 × 1000 × 100 = 1 33333 1:33333 ℎ = 60 ℎ = 60 ℎ = 60 60 = 1 1 ℎ , , 1 ≈ 1 − − − − − − − −(1) , , 1 3 ≈ 1 ∴ 1 ≈ 3 − − − − − − − −(2) (1) (2), ℎ , 1 = 3 , ℎ ℎ 15 , 15 3 = 5 ℎ ℎ 3 30sec ℎ ℎ Now a horizontal line 15 cm long is drawn and is divided into 5 equal parts so that each major division shows one minute. From left staring 0 at 2nd division major units are marked sequentially toward right as 0, 1, 2, 3 and 4. The 1st division is further divided into 6 divisions so that each minor division shows 10 seconds and starting at 0 mark placed earlier the sub-divisions are marked as 10, 20, 30, 40, 50 and 60 toward left. R.F. and unit names are mentioned accordingly. Thus the scale is constructed and the required time is indicated.














































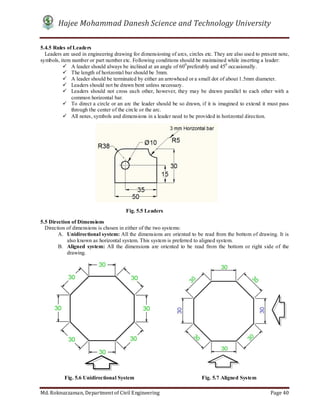

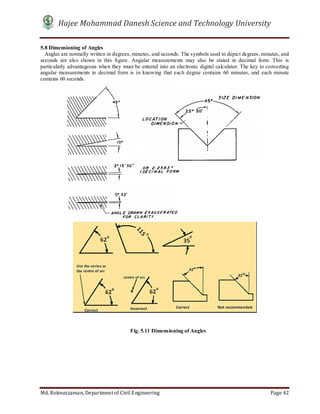







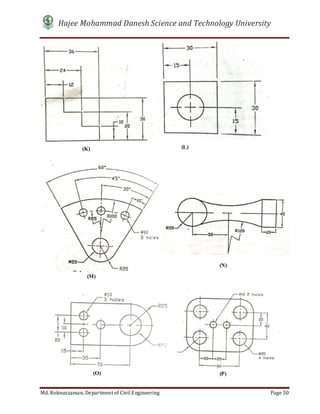





![Hajee Mohammad Danesh Science and Technology University
Md. Roknuzzaman, Department of Civil Engineering Page 56
expand by absorbing or leaving moisture due to temperature effect. Taking measurements from such a drawing
using the proportion mentioned will give some inaccurate result. But if a scale is constructed an drawn during the
preparation of 1st
time, the drawn scale will also shrink or expand in the same proportion to the drawing. Thus if
one take measurements with the help of the drawn scale, accurate measurements will be obtained.
6.6 Information Necessary for Construction of a Scale
Following are the necessary information required for construction of a scale:
The representative fraction (R.F.) of the scale.
The unit or units to be presented.
The maximum length to be measured.
6.6.1 The Representative Fraction (R.F.) or Scale Factor (S.F.)
The ratio of the distance on drawing paper of an object to the corresponding actual distance of the object is
known as the representative fraction (R.F.) or the scale factor (S.F.). It is to be remembered that for finding RF the
distances used for calculation must be in same unit. And being a ratio of same units, R.F. itself has no unit.
Mathematically,
. . =
[ ]
6.6.1.1 Worked out Examples of R.F. Calculation
Example 6.1: In a certain map, 2.5 centimeters of measured length represents 5 hectometers of actual distance.
Calculate R.F. for the scale of this map.
Solution:
Representative Fraction of the scale for this map,
. . =
.
× × × ×
= 1: 20000
Example 6.2: To draw a microscopic element of a machine part, it is to be enlarged in drawing such a manner
that one-fifth of one millimeter is to be represented by 1.5 meters. Find out RF of the scale for this drawing.
Solution:
Representative Fraction of the scale,
. . =
. × × ×
= 7500 7500: 1
Example 6.3: A scale is to be constructed for a drawing of a plot such that 100 square feet of area is to be
represented by 1 square inch. What will be the R.F. of this scale?
Solution:
Here 1 sq. inch represents 100 sq.ft. or we can write 1 ℎ ≈ 100
Taking under root on both sides, we get
1 ℎ ≈ 100
∴ 1 ℎ ≈ 10
, . .=
1
10 × 12
=
1
120
1: 120](https://image.slidesharecdn.com/engineeringdrawingforbeginners-151110071236-lva1-app6892/85/Engineering-drawing-for-beginners-62-320.jpg)
![Hajee Mohammad Danesh Science and Technology University
Md. Roknuzzaman, Department of Civil Engineering Page 57
6.6.2 Units of Measurement
It is modern practice to use metric system of units in engineering drawing. However, sometimes British system
is also used. It is important to have clear understanding about unit conversion in both system. Table 6.2 to Table
6.7 presents the units of measurements, their symbols and conversions.
Table 6.2 Metric Units for Linear Measurement
Table 6.4 Metric Units for Area Measurement
Table 6.6 Metric Units for Volumetric Measurement
1000 cubic millimeters (mm3
) = 1 cubic centimeter (cm3
)
1000 cubic centimeters (cm3
) = 1 cubic decimeter (dm3
)
1000 cubic decimeters (dm3
) = 1 cubic meter (m3
)
6.7 Construction of Plain Scale
Following are the steps for constructing a plain scale
Find out the R.F., if not given directly.
Find out the length of scale
= . . × ℎ ℎ
[Note: If length of object or maximum length to be measured is not mentioned in problem, for
convenience, take the length of scale about 15 cm or 6 inches]
Draw a straight line, preferably horizontal, of required length as found in previous step.
Divide the line into a number of divisions relating to the length of object and maximum length to be
measured such that one segment represents one major unit. Avoid fractions, consider the next integer
value. For instance, if maximum length to be measured is 6.2 km, then number of divisions will be 7.
Place mark 0 at the end of 1st
main division (Remember, not at the starting point of 1st
division) and
mark the other divisions sequentially toward right as 1,2,3….. etc.
Divide the 1st
main division into a number of divisions such that each of these smallest division
represents one sub-unit. For instance if the scale need to measure in feet and inches, number of minor
divisions will be 12. On the other hand if the scale is to measure in centimeters and millimeters or in
meters and 1/10th
of meter number of divisions will be 10.
Mark the sub-unit sequentially toward left as 1, 2, 3…… etc. or 0.1, 0.2, 0.3……. etc. If space is
limited they can be marked after every 2 division like 0, 2,4,….. etc.
Mention the R.F. of the scale below the figure.
Mention the name of main unit and sub-unit either at below or at the respective ends of the scale.
12 inches = 1 foot
3 feet = 1 yard
220 yards = 1 furlong
8 furlong = 1 mile
10 millimeters (mm) = 1 centimeter (cm)
10 centimeters (cm) = 1 decimeter (dm)
10 decimeters (dm) = 1 meter (m)
10 meters (m) = 1 decameter (dam)
10 decameters (dam) = 1 hectometer (hm)
10 hectometers (hm) = 1 kilometer (km)
100 square millimeters (mm2
) = 1 square centimeter (cm2
)
100 square centimeters (cm2
) = 1 square decimeter (dm2
)
100 square decimeters (dm2
) = 1 square meter (m2
)
100 square meters (m2
) = 1 acre (a)
100 acres (a) = 1 hectare
100 hectares = 1 square kilometer (km2
)
144 square inches = 1 square foot
9 square feet = 1 square yard
4840 square yards = 1 acre
640 acres = 1 square mile
1728 cubic inches = 1 cubic foot
27 cubic feet = 1 cubic yard
Table 6.3 British Units for
Linear Measurement
Table 6.5 British Units for Area
Measurement
Table 6.7 British Units for
Volumetric Measurement](https://image.slidesharecdn.com/engineeringdrawingforbeginners-151110071236-lva1-app6892/85/Engineering-drawing-for-beginners-63-320.jpg)
![Hajee Mohammad Danesh Science and Technology University
Md. Roknuzzaman, Department of Civil Engineering Page 58
6.7.1 Worked-out Examples of Plain Scale Construction
Example 6.4: Construct a plain scale to show kilometers and hectometers when 2.5 centimeters are equal to 1
kilometer and long enough to measure upto 5.7 kilometers. Find R.F. of the scale and indicate distances
(i) 4 kilometers and 5 hectometers and (ii) 5.4 kilometers on the scale.
Solution:
. .=
2.5
1 × 10 × 10 × 10 × 10 × 10
=
1
40000
1: 40000
ℎ = . . × ℎ
= × 6 = × 6 × 1000 × 100 = 15
[ To avoid fraction, maximum distance is take 6 km instead of 5.7 km ]
Now a horizontal line 15 cm long is drawn and is divided into 6 equal parts. From left staring 0 at 2nd
division major units are marked sequentially toward right as 0, 1, 2, 3, 4 and 5. The 1st
division is further
divided into 10 divisions and starting at 0 mark placed earlier the sub-divisions are marked after every 2
division as 2, 4, 6, 8 and 10 toward left. R.F. and unit names are mentioned accordingly. Thus the scale
is constructed and the required distances are indicated.](https://image.slidesharecdn.com/engineeringdrawingforbeginners-151110071236-lva1-app6892/85/Engineering-drawing-for-beginners-64-320.jpg)