Base paper

IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 27, NO. 11, NOVEMBER 2012 4667
Extended-Phase-Shift Control of Isolated
Bidirectional DC–DC Converter for Power
Distribution in Microgrid
Biao Zhao, Student Member, IEEE, Qingguang Yu, Member, IEEE, and Weixin Sun
Abstract—This paper points out a phenomenon of power back-flow
in traditional phase-shift (TPS) control of isolated bidirec-tional
full-bridge DC–DC converter (IBDC), and analyzes the ef-fects
which backflow power act on power circulating flow and cur-rent
stress. On this basis, the paper proposes a novel extended-phase-
shift (EPS) control of IBDC for power distribution in micro-grid.
Compared with TPS control, EPS control not only expands
regulating range of transmission power and enhances regulating
flexibility, but also reduces current stress and improves the sys-tem
efficiency. The operation principle of EPS control and the
operation modes of IBDC are analyzed in the paper. By establish-ing
mathematical models of transmission power, backflow power,
and current stress, the paper comparatively analyzes control per-formances
of TPS and EPS control. At last, experimental results
verify the excellent performance of EPS control and correctness of
the theoretical analysis.
Index Terms—Bidirectional DC/DC converter, current stress.,
microgrid, phase-shift control, power distribution, power flow.
I. INTRODUCTION
MICROGRIDS are becoming a reality in a scenario
in which interconnected loads, distributed energy re-sources,
and distributed storage systems can be conjugated and
integrated into grid. The need for more flexible electricity sys-tems,
energy savings, and environmental impact are driving the
development of microgrids [1]–[5].
Generally, microgrids can operate in grid-connected mode
and islanded mode [6], [7]. In the grid-connected mode, the
microgrid is connected to a utility grid, operates in parallel with
the utility, and exchanges power with the utility through the
point of common coupling. However, microgrid disconnects the
utility and transfers into the islanded operation when a fault
occurs in the upstream power grid. And in the islanded mode,
microgrid canwork as an autonomous grid to generate electricity
using distributed energy resources. So it is important to balance
Manuscript received August 10, 2011; revised October 5, 2011 and Novem-ber
13, 2011; accepted December 8, 2011. Date of current version June 20,
2012. This work was supported by the National Natural Science Foundation
of China under Grant 51077076. Recommended for publication by Associate
Editor T.-J. (Peter) Liang.
B. Zhao and Q. Yu are with the Department of Electrical Engineering,
Tsinghua University, Beijing 100084, China (e-mail: zhaobiao112904829@
126.com; yuqingguang@163.com).
W. Sun is with the China Power Engineering Consulting Group Corpora-tion,
North China Power Engineering Co. Ltd., Beijing 100084, China (e-mail:
sunwx1023@163.com).
Color versions of one or more of the figures in this paper are available online
at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TPEL.2011.2180928
demand and supply coming both from the utility and distributed
energy resources.
Moreover, due to not only environmental aspects but also
social, economical, and political interests, many types of re-newable
energy, such as photovoltaic (PV) and wind energy,
have been widely utilized as distributed energy resources in
microgrid [5]. But the variable nature of these renewable en-ergy
systems relies on natural phenomenon, such as sunshine or
wind [8], [9]. Consequently, it is difficult to predict the power
that can be obtained through these prime sources, and the peaks
of power demand do not coincide necessarily with the gener-ation
peaks. Hence, storage energy systems are required if we
want to supply the local loads in an uninterruptible power supply
(UPS) fashion [5], [10].
In order to realize power distribution between energy gener-ation
systems and storage systems in micro grids, various bidi-rectional
DC–DC converters (BDCs) have been proposed as an
everlasting key component to interface between a high-voltage
bus, where an energy generation system such as a fuel cell stack
or a photovoltaic array is installed, and a low-voltage bus, where
usually an energy storage system such as a battery or a super
capacitor is implemented, as shown in Fig. 1 [11]. Generally,
BDC is divided into nonisolated type [12], [13] and isolated
type [11], [14]–[23], and galvanic isolation for BDC is required
for flexibility of system reconfiguration and meeting safety stan-dards
[14], [17]. State-of-the-art isolated bidirectional DC–DC
converter (IBDC) is based on the single-phase and H-bridge
topology with a high-frequency isolation transformer. Fig. 2 de-picts
a typical configuration of IBDC. Compared to traditional
DC–DC converter circuits, this converter has many advantages,
such as electrical isolation, high reliability, easy to realize soft-switching
control, and bidirectional energy flow [14]–[16], [20].
Generally, there are mainly two kinds of control methods for
such topology: traditional pulsewidth modulation (PWM) con-trol
[17]–[19] and phase-shift control. In traditional PWM con-trol,
the cross-connected switch pairs in H-bridge (H1 ), such as
(S1, S4 ) and (S2, S3 ), are switched in turn to transform the high-voltage
V1 from DC to AC, the switches (Q1–Q4 ) in H-bridge
(H2 ) are turned OFF and the current conducts only through the
diodes (M1–M4 ) to transform the voltage from AC to DC, so
the power is transferred from V1 side to V2 side. In the reverse
power flow, the states of S1–S4 and Q1–Q4 are exchanged. This
control method is simple and easy to implement, but it has poor
dynamic performance. And the AC output voltage can only be
lower than DC input voltage in H-bridge inverter, so its regulat-ing
range of voltage is limited.
0885-8993/$31.00 © 2012 IEEE

4668 IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 27, NO. 11, NOVEMBER 2012
Fig. 1. Typical application of BDC for power distribution in microgrid [11].
Fig. 2. Typical configuration of IBDC.
In TPS control [14]–[16], [20], the cross-connected switch
pairs in both H-bridges (H1 and H2 ) are switched in turn to gen-erate
phase-shifted transition square waves to the transformer’s
primary and secondary sides. And the corresponding phase shift
changes the voltage across the transformer’s leakage inductor to
manipulate the power flowdirection and magnitude. This control
method is attracting more and more attention due to its advan-tages
such as small inertia, high dynamic performance, easy to
realize soft-switching control, and so on. But in this method, the
control of the power flow is dependent on transformer’s leak-age
inductor that result in great circulating power and current
stress when the value of V1 /nV2 deviate far from 1, where n is
turns’ ratio of the transformer. And then, the loss in power de-vices
and magnetic components is increased and the efficiency
of converter is reduced. In order to improve the performance of
the IBDC, various control methods were explored [21]–[25]. In
some of these studies [21], [22], the duty ratio of the driving
signals of each semiconductor device is variable, and should be
calculated online, that increases the complexity of the control.
Some studies are focused on how to extend the soft-switching
range [23] or eliminate reactive power [24], the detailed anal-ysis
of steady characteristics is not conducted. In [25], a novel
phase-shift dual-half-bridge converter with an adaptive inductor
was proposed. It utilizes an adaptive inductor as the commuta-tion
inductor to adapt to the change of the output power, which
results in strict requirements of the coiling method of inductor
and the complexity of the control. And it is mainly improve-ment
of hardware design; the control method of the proposed
converter is still TPS control.
In view of the study situation mentioned above, this paper
points out a phenomenon of power backflowin traditional phase-shift
control, and analyzes the effects which backflow power act
Fig. 3. Equivalent circuit of phase-shift control.
on power circulating flow and current stress. On this basis, the
paper presents a novel extended-phase-shift control of IBDC
for power distribution in microgrid. Different from the control
methods mentioned above, this method adds another degree of
freedom to the converter by adjusting the time sequence between
the driving signals of diagonal semiconductor switches, e.g.,
(S1, S4 ) in Fig. 2. It not only has smaller power circulating
flow and current stress, but also expands regulating range of
transmission power and enhances regulating flexibility.
II. PHENOMENON OF POWER BACKFLOW IN TRADITIONAL
PHASE-SHIFT CONTROL
In Fig. 2, we replace the transformer with T-type equivalent
circuit, and considering that the magnetizing inductance of the
transformer is much greater than its leakage inductance, the
magnetizing inductance can be considered as an open circuit.
Therefore, the converter in phase-shift control can be repre-sented
by a simplified scheme comprised of two square waves
voltage sources linked by an inductance L, as shown in Fig. 3.
In Fig. 3, L is the sum of the transformer leakage inductance
and that of the auxiliary inductor L1 , vh1 and vh2 are the equiv-alent
AC output voltages of H1 and H2 in V1 side, respectively,
vL and iL are the voltage and current of inductor L, respectively.
The power-flow direction and magnitude can simply be con-trolled
by adjusting the phase shift between vh1 and vh2. Here
we take the forward power flow (from V1 to V2 ) as an example
to analyze the main operation principle of TPS control.
The main waveforms of IBDC in TPS control are shown
in Fig. 4, where pin is the transient waveform of transmission
power, Ths is a half switching period, and D is the phase-shift
ratio between the primary and secondary voltages of the isola-tion
transformer, where 0 ≤ D ≤ 1.Andwe assume V1 ≥ nV2 in
Fig. 4, the other condition V1 < nV2 can be analyzed similarly.
Because vh1 and vh2 are both square wave AC voltages and their

ZHAO et al.: EXTENDED-PHASE-SHIFT CONTROL OF ISOLATED BIDIRECTIONAL DC–DC CONVERTER 4669
Fig. 4. Waveforms of IBDC in TPS control.
interaction is through the inductor L, so the phase of the primary
current is not always the same as the primary voltage. As can
be seen from Fig. 4, iL is of the opposite phase from vh1 for an
interval of t = t0 ∼ t
0 and t = t2 ∼ t
2 , that is a portion of the
power delivered to the V2 side in one switching period, while
the other portion is sent back to the primary voltage source V1 .
We defined it as backflow power, which is the dark-shaded area
in Fig. 4. For a given transmission power, with the increase of
the backflow power, the forward power also increases to com-pensate
the loss caused by backflow power. Then the circulating
power and current stress are increased, which result in great loss
in power devices and magnetic components and low efficiency
of converter [16], [19]–[23]. In Section IV, we will establish a
mathematical model to analyze it.
III. OPERATION PRINCIPLE OF EXTENDED-PHASE-SHIFT
CONTROL
A. Extended-Phase-Shift Control
In order to significantly decrease the backflow power of the
converter, vh1 should not be confined to square waveforms with
Fig. 5. Waveforms of IBDC in EPS control.
50% duty ratio. For example, if S1 and S4 do not have the same
driving signal but have a phase-shift ratio of D1, as shown in
Fig. 5, the transformer primary voltage will emerge as a three-level
instead of the traditional two-level. Then the behaviors
of iL will also be changed: the backflow-appearance time (t =
t0 ∼ t
0 and t = t2 ∼ t
2 ) in Fig. 4 are divided into two intervals
(t = t0∼t1 , t = t1 ∼ t
1 and t = t3∼t4 , t = t4 ∼ t
4) in Fig. 5,
respectively. And the transformer primary voltage vh1 = 0, i.e.,
backflow power is 0, when t = t0∼t1 and t = t3∼t4. So the
backflow power is decreased for a given transmission power. In
the reverse power flow, we just need to exchange the operating
states of the H-bridges H1 and H2 .
In Fig. 5, D1 is the phase-shift ratio between the driving sig-nals
of S1 and S4 or S 2 and S3 in H-bridge H1 , we defined its
inner phase-shift ratio, where 0 ≤ D1 ≤ 1. D2 is the phase-shift

Fig. 6. Operation modes of IBDC in EPS control. (a) Mode 1. (b) Mode 2. (c) Mode 3. (d) Mode 4. (e) Mode 5. (f) Mode 6. (g) Mode 7. (h) Mode 8.
ratio between the primary and secondary voltages of the isola-tion
transformer, we defined its outer phase-shift ratio, where
0 ≤ D2 ≤ 1 and 0 ≤ D1+D2 ≤ 1. In fact, compared to the
TPS control, there is not only the outer phase-shift ratio but also
the inner phase-shift ratio in the proposed EPS control, which
will decrease the current stress, expands regulating range of
transmission power and enhances regulating flexibility.
B. Operation Modes of IBDC in Extended-Phase-Shift Control
To simplify the process of the analysis, we assume that the
converter has reached steady operation states. From Fig. 5, the
switching cycle can be divided into eight operation modes which
are explained as follows:
1) Mode 1 (t0–t1 ): Fig. 6(a) shows the equivalent circuit for the
mode 1. Just before t0, S2 and S3 are conducting. The current iL
is in negative direction. At t0, S3 is turned OFF and S4 is turned
ON at zero current, and D4 starts to conduct. On the secondary
side, the current is carried from L to V2 by M2 and M3. The
voltage across L is clamped at nV2 , and the current iL decreases
linearly. This mode ends up when S2 is turned OFF. During this
mode, the current of L is
iL (t) = iL (t0) + nV2
L
(t − t0 ). (1)
2) Mode 2 (t1–t
1 ): Fig. 6(b) shows the equivalent circuit for
mode 2. If current iL is still in negative direction at t1 then at
t1, S2 is turned OFF and S1 is turned ON at zero current, iL
is carried from L to V1 by D1 and D4 . On the secondary side,
the current is carried from L to V2 by M2 and M3 . The voltage
across L is clamped at V1+nV2 , and iL still decreases linearly.
This mode ends up with iL decreasing to zero. During this mode,
iL is
iL (t) = iL (t1) + V1 + nV2
L
(t − t1 ). (2)

3) Mode 3 (t
1–t2 ): Fig. 6(c) shows the equivalent circuit for
the mode 3. At t
1 , the polarity of iL changes from negative to
positive. And because the driving signals of S1, S4, Q2 , and
Q3 are already on, so S1, S4, Q2 , and Q3 start to conduct.
The voltage across L is clamped at V1 + nV2 , and iL increases
linearly. This mode ends up when Q2 and Q3 are turned OFF.
During this mode, iL is the same with (2).
4) Mode 4 (t2 – t3 ): Fig. 6(d) shows the equivalent circuit for
the mode 4. At t2, Q2 and Q3 are turned off and Q1 and Q4
are turned on at zero current. M1 and M4 start to conduct. The
voltage across L is clamped at V1–nV2 , and iL still increases
linearly due to V1 ≥ nV2 . This mode ends up when S4 is turned
OFF. During this mode, iL is
iL (t) = iL (t2) + V1 − nV2
L
(t − t2 ). (3)
5) Mode 5 (t3 – t4 ): Fig. 6(e) shows the equivalent circuit for
mode 5. At t3, S4 is turned OFF and S3 is turned ON at zero
current, D3 starts to conduct. On the secondary side, the current
is carried from L to V2 by M1 and M4 . The voltage across L
is clamped at –nV2 , and the current iL decreases linearly. This
mode ends up when S1 is turned OFF. During this mode, the
current of L is
iL (t) = iL (t3) +
−nV2
L
(t − t3 ). (4)
6) Mode 6 (t4 – t
4 ): Fig. 6(f) shows the equivalent circuit for
mode 6. If current iL is still in positive direction at t4 , then at
t4, S2 is turned OFF and S1 is turned ON at zero current, iL
is carried from L to V1 by D2 and D3 . On the secondary side,
the current is carried from L to V2 by M1 and M4 . The voltage
across L is clamped at –V1–nV2 , and iL still decreases linearly.
This mode ends up with iL decreasing to zero. During this mode,
iL is
iL (t) = iL (t4) +
−V1 − nV2
L
(t − t4 ). (5)
7) Mode 7 (t
4–t5 ): Fig. 6(g) shows the equivalent circuit for
the mode 7. At t
4 , the polarity of iL changes from positive to
negative. And, because the driving signals of S2, S3, Q1 , and
Q4 are already ON, so S2, S3, Q1 , and Q4 start to conduct.
The voltage across L is clamped at –V1–nV2 , and iL increases
linearly. This mode ends up when Q1 and Q4 are turned OFF.
During this mode, iL is the same with (5).
8) Mode 8 (t5 – t6 ): Fig. 6(h) shows the equivalent circuit for
the mode 8. At t5, Q1 and Q4 are turned OFF and Q2 and Q3
are turned ON at zero current. M2 and M3 start to conduct. The
voltage across L is clamped at –V1+nV2 , and iL still increases
linearly due to V1 ≥ nV2 . This mode ends up when S3 is turned
OFF. During this mode, iL is
iL (t) = iL (t5) +
−V1 + nV2
L
(t − t5 ). (6)
According to the above analysis, the transformer primary
voltage vh1 = 0, and there is no backflow power in modes 1
and 5. So the whole backflow power is decreased for a given
transmission power. In fact, if iL has dropped to zero before t1
or t4 , then the backflow power will be eliminated, as shown in
Fig. 7(a). In this case, modes 2 and 6 in Fig. 6 will be replaced
by mode 2 and 6 in Fig. 7(b) and (c), respectively.
9) Mode 2 (t
1–t1 ): Fig. 7(b) shows the equivalent circuit
for mode 2. At t
1 , the polarity of iL changes from negative
to positive. And because the driving signals of S2, S4, Q2 , and
Q3 are already ON, so D2, S4, Q2 , and Q3 start to conduct.
The voltage across L is clamped at nV2 , and iL still increases
mode, iL is the same with (1).
10) Mode 6 (t
4–t4 ): Fig. 7(c) shows the equivalent circuit
for mode 6. At t
4 , the polarity of iL changes from positive to
negative. And because the driving signals of S1, S3, Q1 , and
Q4 are already ON, so D1, S3, Q1 , and Q4 start to conduct.
The voltage across L is clamped at –nV2 , and iL still increases
mode, iL is the same with (4).
IV. ANALYSIS AND COMPARISONS OF TPS AND EPS CONTROL
A. Low-Frequency Average Model
According to the above analysis, assuming t0 = 0, then we
have t1 = D1Ths, t2 = D2Ths, t3 = Ths, t4 = Ths+D1Ths, t5 =
Ths+D2Ths, and t6 = 2Ths. The average current of the inductors
over one switching period (2Ths) should be zero in steady state;
thus from (1) to (6), we can derive
iL (t0) = − nV2
4fsL
[k(1 − D1) + (2D1 + 2D2 − 1)] (7)
iL (t1) = − nV2
4fsL
[k(1 − D1) + (2D2 − 1)] (8)
iL (t2) = nV2
4fsL
[k(2D2 + D1 − 1) + 1] (9)
where fs = 1/(2Ths) is switching frequency, k = V1/nV2 is the
voltage conversion ratio, and we assume k ≥ 1 in the paper,
the other condition k 1 can be analyzed similarity. When the
power flows from V1 to V2 , the current stress of converter under
EPS control is

max = |iL (t0 )| = nV2
i
4fsL
[k(1 − D1) + (2D1 + 2D2 − 1)].
(10)
The transmission power is
P
=
1
Ths

Th s
0
vh1iL (t)dt
= nV1V2
2fsL

D2(1 − D2) +

. (11)
1
2D1(1 − D1 − 2D2 )

Fig. 7. (a) Waveforms of IBDC in EPS control when the backflow power is zero. (b) Mode 2 of IBDC in EPS control when the backflow power is zero. (c)
Mode 6 of IBDC in EPS control when the backflow power is zero.
The backflow power is
P

bf =
1
Ths

t
1
t1
vh1 |iL (t)|dt
= nV1V2 [k(1 − D1) + (2D2 − 1)]2
16fsL(k + 1)
(12)
where iL (t1 ) 0, from (8), we have
k
1 − 2D2
1 − D1
. (13)
When k ≤ (1–2D2 )/(1–D1 ), the backflow power is zero. In (7)–
(13), the constraints are k ≥ 1, 0 ≤ D1 ≤ 1, 0 ≤ D2 ≤1, and
0 ≤ D1+D2 ≤ 1. Similarly, from Fig. 4, the current stress of
converter under TPS control is
imax = nV2
4fsL
(2D − 1 + k). (14)
The transmission power is
P = nV1V2
2fsL
D(1 − D). (15)
The backflow power is
Pbf = nV1V2 [k + (2D − 1)]2
16fsL(k + 1) . (16)
In (14)–(16), the constraints are k ≥ 1 and 0 ≤ D ≤ 1.
Theoretically, when the load is set as resistance R, from (11),
we can derive
V2 = nV1R
2fsL

D2(1 − D2) +
1
2D1(1 − D1 − 2D2 )

. (17)
With the variation of D1 and D2, we have
0 ≤ V2 ≤ nV1R
8fsL
. (18)
Similarly, from (15), the output voltage range in the TPS control
can be achieved. In fact, the output voltage range in the EPS
control is the same as that in the TPS control. And its main
benefit lies in that the power circulating flow and current stress
are both reduced for a given output power; therefore, it leads
to the improvement of the converter’s overall efficiency. Theory
and experiment analysis of the paper are centering on these
special characteristics of EPS control as well.
B. Comparative Analysis of Transmission Power
For the convenience of analysis, the unified transmission
power p and p are defined as
⎧⎪⎪⎨
⎪⎪⎩
p = P
PN
= 4D2(1 − D2) + 2D1(1 − D1 − 2D2 )
p = P
PN
= 4D(1 − D)
(19)

Fig. 8. Relation curves of the unified transmission power p with D1 and D2 . (a) 3-D curves. (b) 2-D curves.
where
PN = nV1V2
8fsL
. (20)
When taking that the outer phase-shift ratio (D2) in EPS
control is equal to the phase-shift ratio (D) in TPS control, the
3-D curves of the unified transmission power p and p varied with
D1 andD2 shown in Fig. 8(a). As can be seen from Fig. 8(a), with
different D1 , p will be different with p. And the EPS control
can achieve larger transmission power than the TPS does when
0 ≤ D2 0.5. In fact, from (19), we can derive
p

max = 1− (1 − 2D2 )2
2
(21)
where 0 ≤ D2 0.5 and D1 = (1-2D2 )/2.
p

max = 4D2(1 − D2 ) (22)
where 0.5 ≤ D2 1 and D1 = 0.
p

min = 2D2(1 − D2 ) (23)
where D1 = 1-D2 .
From (21) to (23), Fig. 8(a) can be converted to a 2-D picture,
as shown in Fig. 8(b). The dashed line is the regulating curve
of transmission power in TPS control, and the dark-shaded area
is the regulating area of transmission power in EPS control.
From Fig. 8(b), due to the addition of D1 , the regulating range
of transmission power is changed from the single curve to the
2-D area. With the same outer phase-shift ratio (D2 = D), the
EPS control offers wider power transmission range than the TPS
control does, and the maximum value is determined by (21) and
(22) while the minimum value is determined by (23). Due to the
addition of D1 , the regulating flexibility of transmission power
is also enhanced.
Considering that the basic prerequisite for comparative analy-sis
of backflow power and current stress is that the transmission
power of TPS and EPS control are the same. In the follow-ing
analysis, we take operating points A/A4 , B/B3 , and C/C2 as
characteristic points of TPS control in different operating ar-eas,
where A(D = 1/8), A4 (D = 7/8), B(D = (2 − 21/2)/4),
B3 (D = (2+21/2)/4), C(D = 1/4), and C2 (D = 3/4), then the
characteristic points of EPS control are A1 /A2 /A3 , B1 /B2 , and
C1 .
C. Comparative Analysis of Backflow Power
Considering the relationship between the backflow power
and the transmission power, the unified backflow power Mbf
and M
bf are defined as
M

bf =
P
bf
PN
=
[k(1 − D1) + (2D2 − 1)]2
2(k + 1)
(24)
Mbf = Pbf
PN
=
[k + (2D − 1)]2
2(k + 1) . (25)
The basic prerequisite for comparative analysis of backflow
power is that the transmission power of TPS and EPS control
are the same. From (11) and (15), we have
4D(1 − D) = 4D2(1 − D2) + 2D1(1 − D1 − 2D2 ). (26)
With the specified value of D1 and D2 in EPS control, the
phase-shift ratio D in TPS control can be obtained
D=
⎧⎪⎪⎨
⎪⎪⎩
D =
1 −

1 − 4D2(1 − D2 ) − 2D1(1 − D1 − 2D2 )
2
D =
1 +

1 − 4D2(1 − D2 ) − 2D1(1 − D1 − 2D2 )
2
.
(27)
Using (24), (25), and (27), and assuming k = 5, the 3-D curve of
the unified backflow power varied with D1 and D2 can be shown
in Fig. 9. As can be seen from Fig. 9, the backflow power in
TPS and EPS control are the same when D1 = 0. And due to the
addition of D1 , with the same transmission power, the backflow
power in TPS control is larger than that in EPS control, and the
condition of D = D generates larger backflow power than the
condition of D = D does.
The contour lines in Fig. 8(b) show that there are infinite
combinations of (D1 , D2 ) in EPS control for the same transmis-sion
power in TPS control. Considering the different qualities
of EPS control in different operating points, we will analyze the

Fig. 9. 3-D curves of the unified backflow power M
bf varied with D1 and
D2 .
optimal operating point of backflow power. From (26), we have
D1 =
⎧⎪⎪⎨
⎪⎪⎩
D1
=
1 − 2D2 −

2(1 − 2D)2 − (1 − 2D2 )2
2
D
1 =
1 − 2D2 +

2(1 − 2D)2 − (1 − 2D2 )2
2
.
(28)
For D
1 ≥ D1
, from (24), we have
M

bf (D
1
) ≥ M

bf (D

1 ). (29)
Substituting D1 = D
1 into (24), the function of M
bf and D2
can be obtained
M

bf min(D2 )
=
[k(1−

2(1 − 2D)2−(1 − 2D2 )2)+ 2(k + 2)D2 − 2]2
8(k + 1)
(30)
where |1–2D2| ≤ 21/2 |1–2D| and 0 ≤ D2 ≤ 1. Solving (30)
with constrained optimization methods, we can derive
1) when 0 ≤ D (2–21/2)/4
M

bf min(D2)=M

bf min(0) =
[k − 2 − k

2(1 − 2D)2 − 1]2
8(k + 1)
(31)
where
⎧⎨
⎩
D1 =
1 +

2(1 − 2D)2 − 1
2
D2 = 0
(32)
2) when (2–21/2)/4 ≤ D 1/2
M

bf min(D2) = M

bf min

1 −
√
2(1 − 2D)
2

=
√
2 − 1)k − 2 + 2(k + 2)D]2
[(
4(k + 1)
(33)
where
⎧⎪⎪⎨
⎪⎪⎩
D1 =
√
2(1 − 2D)
2
D2 =
1 −
√
2(1 − 2D)
2 .
(34)
In Fig. 8(b), we take operating points A, B, C, A1 /A2 /A3 , B1 /B2 ,
and C1 as characteristic points of TPS and EPS control in differ-ent
operating areas, from (19) to (21), and (26), we have: A1 (D2
= 0, D1 = (4+21/2)/8), A1
(D2 = 0, D1 = (4–21/2)/8), A2 (D2
= (4–21/2)/8, D1 = (4+21/2)/8), A3 (D2 = (4+21/2)/8, D1 =
(4–21/2)/8), B1 (D2 =0,D1 =1/2), B2 (D2 =1/2,D1 =1/2), and
C1 (D2 = (2–21/2)/4, D1 = 21/2/4). Fig. 10 shows the curves of
the unified backflow power varied with voltage conversion ratio
k in TPS and EPS control for the same transmission power.
D. Comparative Analysis of Current Stress
For the convenience of analysis, the unified current stress G
and G are defined as
G
= i
max
IN
= 2[k(1 − D1) + (2D1 + 2D2 − 1)] (35)
G = imax
IN
= 2(2D − 1 + k) (36)
where
IN = PN
V1
= nV2
8fsL
. (37)
Using (27), (35), and (36), and assuming k = 5, the 3-D curve
of the unified current stress varied with D1 and D2 as shown in
Fig. 11. As can be seen from Fig. 11, the current stress in TPS
and EPS control are the same when D1 = 0. And due to the
addition of D1 with the same transmission power, the current
stress in TPS control is larger than that in EPS control, and the
condition of D = D generates larger current stress than the
condition of D = D does.
Likewise, the optimal operating point of current stress can be
analyzed. For D
1 ≥ D1
, from (35), we have

G(D1
) ≤ G(D
1 ) k 2
G(D
1 ) ≤ G(D1
) k ≥ 2.
(38)
That is,

min(D2) =
G
⎧⎪⎪⎨
⎪⎪⎩

2(1 − 2D)2 − (1 − 2D2 )2
(k − 2)
+2kD2 +k k2

2(1 − 2D)2 − (1 − 2D2 )2
(2 − k)
+2kD2 +k k≥ 2
(39)
where |1–2D2| ≤ 21/2 |1–2D| and 0 ≤ D2 ≤ 1. Solving (39)
with constrained optimization methods, we can derive
1) when 0 ≤ D (2–21/2)/4

min(D2) =
G

2(1 − 2D)2 − 1 +k k2

(k − 2)

2(1 − 2D)2 − 1 +k k≥ 2
(2 − k)
(40)

Fig. 10. Curves of the unified backflow power M
bf varied with voltage conversion ratio k. (a) A and A4 in TPS control and A1 , A
1 , A2, and A3 in EPS control.
(b) B and B3 in TPS control and B1 and B2 in EPS control. (c) C and C2 in TPS control and C1 in EPS control.
Fig. 11. 3-D curves of the unified current stress G varied with D1 and D2 .
where
⎧⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
D1 =
⎧⎪⎪⎨
⎪⎪⎩
1 −

2(1 − 2D)2 − 1
2 k 2
1 +

2(1 − 2D)2 − 1
2 k ≥ 2
D2 = 0.
(41)
According to (32) and (41), when k≥2, the optimal operating
points of backflow power and current stress are the same. From
(36) and (40), we can derive

G ≤ G
min k k0
G
min
≤G k≥ k0
(42)
k0 = 2− 1 +

2(1 − 2D)2 − 1
2(1 − D)
(43)
2) when (2–21/2)/4 ≤ D 1/2

min(D2) = k(2
G
√
2D + 2 −
√
2) (44)
where
⎧⎪⎪⎨
⎪⎪⎩
D1 =
√
2(1 − 2D)
2
D2 =
1 −
√
2(1 − 2D)
2 .
(45)
From (36) and (44), we can derive

G ≤ G
min k k0
G
min
≤G k≥ k0
(46)
where
k0 =
√
2. (47)
According to the above analysis, when k ≥ k0 , the current stress
in EPS control is less than that in TPS control. Likewise, we take
operating points A, B, C, A1 /A2 /A3 , B1 /B2 , and C1 as character-istic
points of TPS and EPS control in different operating areas.
Then the curves of the unified current stress varied with voltage
conversion ratio k for the same transmission power shown in
Fig. 12.
As can be seen from Fig. 12, in all operating areas, the current
stress increases with the increase of voltage conversion ratio k.
The EPS control can take different operating points to ensure
that the current stress is less than the TPS control when k ≥ k0 ,
and the minimum value is obtained at A1 , B1 , and C1 , which
agrees well with the aforementioned theoretical analysis.
V. EXPERIMENTAL RESULTS
In order to verify the aforementioned analysis, a laboratory
prototype is constructed based on TMS320F2812 DSP. And the
main parameters of converter are shown in Table I.
In order to verify the power regulating capacity of EPS con-trol,
the input voltage and the output load are specified as 220V
and 6 Ω, respectively. Fig. 13 shows the curves of the transmis-sion
power varied with D1 and D2 . As can be seen from Fig. 13,
in EPS control, the transmission power can be regulated both by
D1 and D2 , and due to the addition of D1 , the regulating range

Fig. 12. Curves of the unified current stress G varied with voltage conversion ratio k. (a) A and A4 in TPS control and A1 , A1
, A2 , and A3 in EPS control. (b) B
and B3 in TPS control and B1 and B2 in EPS control. (c) C and C2 in TPS control and C1 in EPS control.
Fig. 13. Curves of the transmission power varied with D1 and D2 . (a) Curves of the transmission power varied with D1 when D2 is specified. (b) Curves of the
transmission power varied with D2 when D1 is specified.
TABLE I
MAIN PARAMETERS OF PROTOTYPE
of transmission power is changed from the single curve to the
2-D area.With the same outer phase-shift ratio (D2 = D 0.5),
the EPS control (D1= 0) can offer wider power transmission
range than the TPS control (D1 = 0) does, that will enhance
regulating flexibility. In addition, Fig. 13 shows that there are
many different combinations of (D1 , D2 ) in EPS control for the
same transmission power in TPS control. And the maximum
and minimum values of transmission power are obtained about
at D1+D2 = 0.5 and D1+D2 = 1, respectively, which agrees
well with the aforementioned theoretical analysis.
In order to verify the backflow power characterization of EPS
control, the transmission power and output voltage are both
in closed-loop control for 380W and 48V, respectively, the
transient waveforms of transmission power with input voltage
V1 = 220V is shown in Fig. 14(a), and the curves of backflow
power varied with input voltage V1 and inner phase-shift ratioD1
is shown in Fig. 14(b). It can be seen from Fig. 14, the backflow
power is bound up with input voltage V1 and inner phase-shift
ratio D1 , and it decreases with the increase of D1 and increases
with the increase of voltage conversion ratio k = V1 /(nV2 ).
Under different experimental conditions, the EPS control always
can generate less backflow power than the TPS control does, and
the minimum point of current stress is the minimum point of

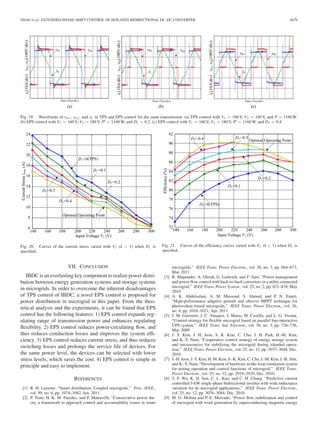
Fig. 14. (a) Transient waveforms of the transmission power when D1 is specified. (b) Curves of the backflow power varied with V1 when D1 is specified.
Fig. 15. Waveforms of vh1 , vh 2 , and iL in TPS and EPS control for the same transmission. (a) TPS control with V1 = 220V, V2 = 48V, and P = 380W. (b)
EPS control with V1 = 220V, V2 = 48V, P = 380W, and D1 = 0.2. (c) EPS control with V1 = 220V, V2 = 48V, P = 380W, and D1 = 0.4.
backflow power when V1 200 (i.e., k200/(2∗48)≈2), which
agrees well with the aforementioned theoretical analysis.
Fig. 15 shows the experimental waveforms of vh1, vh2 , and
iL in TPS and EPS control for the same transmission power, and
Fig. 16 shows the curves of current stress varied with V1 and
D1 . It can be seen that current stress is also bound up with input
voltage V1 and inner phase-shift ratio D1 , and it decreases with
the increase of D1 and increases with the increase of voltage
conversion ratio k = V1 /(nV2 ). Under different experimental
conditions, the EPS control always can generate less current
stress than the TPS control does.When the converter is operating
in the optimal point, the stress current achieves the minimum
value, which is consistent with the aforementioned theoretical
analysis.
Under the same experimental conditions with Figs. 14(b) and
16, Fig. 17 shows the efficiency curves of the converter in both
control methods. It can be easily found that the EPS control
can achieve higher efficiency than the TPS control, especially in
large voltage conversion ratio condition. And when the converter
Fig. 16. Curves of the current stress varied with V1 when D1 is specified.

Base paper

More Related Content

Base paper