Generalization of graph-based active learning relaxation strategies across materials

The urgent need to address climate and societal challenges has prompted the search for innovative solutions, and new material design and discovery have emerged as critical pathways. For instance, new catalysts are being explored for various crucial chemical reactions such as nitrogen reduction to replace the energy-intensive Haber-Bosch process [1, 2], and alcohol dehydrogenation for energy storage applications [3]. Metal oxides are being investigated as catalysts for oxygen reduction and evolution reactions in fuel cells [4, 5]. With the continued advancements in simulation tools and increased computing power, we can harness the power of computational chemistry to further accelerate the process of materials discovery. By utilizing computational techniques, researchers can rapidly screen a vast space of chemical compositions, structures, and properties that would otherwise be prohibitively expensive and time-consuming to explore experimentally [6, 7]. Simulations can also provide valuable insights into the underlying reaction mechanisms, allowing for the optimization of material performance.

However, the computational cost of first-principles simulations becomes infeasible for large chemical spaces. In these cases, one prominent approach in accelerating material discovery is through the use of machine learning (ML) methods, which leverage large databases and advanced algorithms to predict the properties and performance of materials. A properly-trained ML model is vastly lower in computational cost than computational tools such as density functional theory (DFT) and can have comparable accuracy, provided it is being applied on sufficiently similar systems to the training data [8]. The development of large material datasets, such as the Open Catalyst 2020 (OC20) Dataset and Open Catalyst 2022 (OC22) Dataset for metal and metal-oxide materials [9, 10], the CoRE [11], CSD MOF [12], QMOF [13], MOFX-DB [14] for metal organic frameworks (MOFs), and Database of Zeolite Structures [15] and Zeo-1 [16] for zeolites, has enabled data-driven materials modeling research on these materials classes. Remarkable progress has been made in the development of ML models for accurate calculation of interatomic potentials and prediction of materials properties. Graph neural network (GNN) models are specifically designed to handle the inherent graph-like structure of molecules and crystals, where atoms and bonds are represented as nodes and edges in a graph. This allows GNN models to capture the complex interactions between atoms. GNN models such as GemNet [17], GemNet-OC [18], SCN [19], eSCN [20], and M3GNeT [21], can learn vast amounts of chemical information from training data, facilitating the efficient screening of materials and identifying promising candidates for specific applications. For example, the present leading ML model on the Open Catalyst Project (OCP) Leaderboard can achieve a total energy mean absolute error (MAE) as low as 0.22 eV on OC20-like catalyst structures.

Training ML models on large datasets can be time-consuming and computationally demanding, especially in the field of molecular modeling, where diverse chemical structures and properties are involved. One approach to mitigate this challenge is to utilize transfer learning. Transfer learning allows a model to leverage the knowledge and representations learned during pretraining to initialize its parameters for a new dataset, significantly reducing the need for extensive data and computational resources in training [22]. In our prior work, we proposed the Fine-Tuning Accelerated molecular simulations framework (Finetuna) [23] as a promising implementation of online transfer learning with pre-trained ML models. Finetuna utilizes an active querying strategy to determine when to perform a DFT calculation and fine-tune the ML model using the DFT results. More specifically, we benchmarked Finetuna performance on a set of catalyst systems from the OC20 validation set with a GemNet model trained on the OC20 training data. Finetuna demonstrated that local optimizations of OC20-like systems can be greatly accelerated without sacrificing accuracy, as evidenced by a reduction of 90% DFT calculations compared to a baseline approach. We note that the Finetuna framework is one of many online active learning approaches for accelerating atomistic simulations. Other on-the-fly active learning frameworks typically start from scratch, using Gaussian process models or simpler neural network potentials [24–29].

In this work, we seek to extend Finetuna to different out-of-domain chemical systems and gain insights into the capabilities and limitations of the workflow. We conduct a case study of the Finetuna workflow on three groups of materials, namely ($C_{\gt2}$) alcohols, metal oxides, and three-dimensional (3D) structures, for different applications. While the OC20 dataset is limited to the exploration of small ($C_{\unicode{x2A7D} 2}$) adsorbates, we explore the adsorption of $C_{\gt2}$ alcohol-to-ketone intermediates in this work. We also explore metal-oxide catalysts and the structures of zeolites and MOFs which significantly deviate from the catalyst surfaces in the original OC20 dataset. Finally we examine the effect of spin polarization and systems with significantly more atoms than those in the training dataset, both factors that significantly decrease computational speed of DFT. We introduce new querying strategies for these systems with our best-performing Finetuna strategy capable of reducing DFT calls by 80% for both ($C_{\gt2}$) alcohol and 3D structure systems and 42% for oxide systems.

2.1. Finetuna workflow

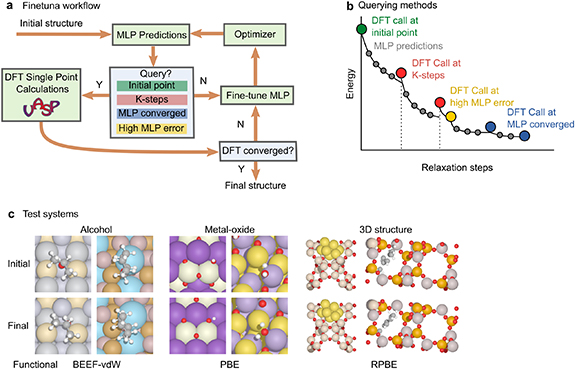
The active learning workflow accelerates geometric optimizations using a pre-trained GNN for fast force estimations. As shown in figure 1, the atomic structure is evaluated by the machine learning potential (MLP), and if a querying criterion is met, such as force convergence is reached or a step threshold is exceeded, a DFT single-point calculation will be triggered (also referred to as a 'parent call'). The DFT-calculated forces are used to fine-tune the MLP. The optimizer uses the atomic forces to update the structure, and the MLP is used for force prediction. Similar to other relaxation processes, the convergence criterion is based on the maximum force in the system.

Zoom In Zoom Out Reset image size

In the Finetuna workflow, many components, e.g. the ML model, the DFT functional and software, the optimizer, and the querying strategy, can be modified to suit specific systems. The choice of the MLP includes all the available pre-trained models, such as the GemNet model trained on OC20 dataset, the GemNet model trained on OC22 dataset, the GemNet-OC model trained on both OC20 and OC22 datasets, etc. We refer to these models as GN-OC20, GN-OC22, GNOC-OC20+22, respectively. The selection of the DFT functional depends mostly on the chemical system of interest; we discuss this further in section 2.2. We limit the DFT code to the Vienna Ab initio Simulation Package (VASP) for the majority of this work to be consistent with the OC20 and OC22 dataset [30–34], and the optimizer to Broyden-Fletcher-Goldfarb-Shanno (BFGS) in the Atomic Simulation Environment Python package (ASE) in order to eliminate variations arising from differences between optimizers [35]. Interfaces to other DFT codes, i.e. Quantum Espresso [36, 37], can be found in the GitHub repository [38], and a detailed comparison of different optimizers can be found in the prior work [23].

The querying strategy determines when a DFT calculation is performed. The four main strategies are demonstrated in figure 1(c). 'Initial point' queries at the initial structure. 'K-steps' determines the lower bound of querying frequency, similar to [23]. The 'MLP converged' strategy queries when the maximum force from ML prediction is less than the convergence criterion. We also introduce a new strategy, labeled as 'high MLP error' in figure 1. After every DFT evaluation and retraining, we use the finetuned MLP to evaluate the current image. The training error is defined as the L2 norm of the difference between the DFT forces and the retrained MLP prediction. If the training error exceeds a set threshold, DFT will be queried for the following frame again. This approach is needed for high-error systems because training on a single frame may not improve the model's prediction enough to allow the framework to correctly converge. This increases the overall frequency with which the model is retrained for challenging systems, when a single DFT query does not sufficiently increase model accuracy, but otherwise does not affect training hyperparameters.

The baseline Finetuna framework uses the GN-OC20 model as the MLP, and queries the parent calculator at the initial point, every 30 ML steps, or when the ML-predicted maximum force is below the convergence criterion (in this work, 0.05 eV Å⁻¹). The baseline strategy is applied to all systems discussed herein. However, the GN-OC20 model exhibits different levels of accuracy on the different types of systems tested in this work. We expect these differences to be caused by how well-represented those systems are in the OC20 training dataset. This, in turn, should affect how conservative the user ought to be in setting the Finetuna algorithm querying strategy. Systems that lie further outside the domain of the training data should require more training, and predictions by the model should be less trustworthy. Therefore, we also test different pre-trained MLPs for the oxide systems, and apply the additional query by high MLP error to the 3D structure systems. The detailed strategies will be further explained in section 2.2.

2.2. Chemical systems

We selected 27 alcohol-to-ketone systems, 10 oxide systems, and 81 3D structure systems and performed both VASP BFGS and Finetuna relaxations. The systems that experienced convergence issues with VASP BFGS and the systems that failed due to memory limitations are excluded from this section. A full list of the tested systems and results can be found in the Supporting Information. The size of the chemical systems in the experiment varied from 50 to 250 atoms. We report the energy difference between the VASP BFGS and Finetuna relaxations in eV/atom to facilitate comparison. We also perform a related benchmark of the Finetuna algorithm using Quantum Espresso instead of VASP as the parent calculator in section S3 of the supporting information.

A summary of the overall performance of Finetuna compared to VASP BFGS can be found in table 1, and a plot of the individual runs is shown in figure 2. For each class of systems, we evaluate the efficiency of the Finetuna workflow by calculating the ratio between the total number of DFT calls with Finetuna relaxation and that with VASP BFGS. This metric is referred to as the percentage DFT calls and represents the overall saving of DFT calculations. The unconverged Finetuna runs are labeled in red crosses in figure 2. We found that none of the metal-oxide systems converged with the baseline GN-OC20 model. This is not surprising due to the lack of oxide systems and spin polarization information in the OC20 training data. For simplicity, the results from Finetuna with GN-OC22 model are shown in figure 2, and the comparisons with other models can be found in the supporting information figure S1. In general, Finetuna underperforms on both accuracy and speed when compared to the results in [23] across all three system types. We believe this is the result of a significant domain shift, which should make realigning the GNN model with fine-tuning slower and less accurate. We consider magnetic effects and 3D structural effects to be the most significant causes of domain shift. By increasing the conservativeness in the Finetuna algorithm through repeated training when errors are high, the overall parent calls can be brought below 20% for alcohol-to-ketones and the 3D structures, and 58% for oxide systems.

Zoom In Zoom Out Reset image size

Across alcohol-to-ketones, metal oxides, and 3D structure systems, there are a number of cases where Finetuna does not converge. As shown in figure 3, most of the unconverged cases have observed high ML predicted forces (> 5.0 eV Å⁻¹) across the entire relaxation trajectory. This implies that for trajectories where the MLP made a large force prediction, they generally should not be trusted to converge, and should be terminated early. In addition, we would expect that (provided initial structure guesses are reasonable), the occurrence of such a large force would indicate that the system has moved to a less realistic region of the configuration space and any local minimum it finds would likely be less physically meaningful. The only exceptions to this are with a few of the alcohol-to-ketones systems, where the trajectory slowly converged (exceeding 100% of the DFT parent calls) despite the high error. Interestingly, these systems do not appear to find significantly different local minima from the original DFT relaxation, so in these cases, it would appear that Finetuna took a somewhat roundabout route to find a very similar result.

Zoom In Zoom Out Reset image size

For the oxide systems, we found that the potential energy surfaces are generally more complicated, as evidenced by the discrepancies in the relaxed energy from the two DFT calculations (VASP BFGS and VASP conjugate gradient (CG) in figure S1). The total magnetization (M) is given by the net spin of the electrons in the system:

$$\begin{equation} M = \mu_{\text{B}}\int\left( n_\uparrow -n_\downarrow \right)d^3r, \end{equation} \tag{ 1 }$$

where µ_B is the Bohr magneton, and $n_\uparrow$ and $n_\downarrow$ represent spin densities. For our purposes, M represents the extent of spin polarization in a given system. Figure 4 shows a case where relaxation with two different models led to nearly identical sets of atomic positions but considerably different magnetizations and energies. The spin polarization adds another degree of freedom to the local minimization process and breaks the one-to-one mapping between atomic structure and potential energy presumed by GemNet. Additionally, as previously mentioned, the ML model we use in this work sets a local cutoff when representing the atomic structure, and is unable to capture long-range interaction from magnetic effects. This suggests that the ML potential and the performance of the algorithm may be compromised when applied to spin-polarized systems, and highlights the importance of developing MLPs, such as CHGNET [48], that effectively capture magnetic information for these applications.

Zoom In Zoom Out Reset image size

In this study, we conducted experiments to assess the performance of the Finetuna workflow on various chemical systems including alcohol-to-ketones, metal oxides, and MOFs. Our findings revealed that, while showing promising results in the original domain (OC20-like systems) with a significant reduction of DFT calls by 90%, Finetuna was less performant on these out-of-domain systems. The results show that we were able to reduce the number of DFT calls by 85% for alcohol-to-ketones systems, 49% for oxide systems, and 82% for MOF systems, with a few unconverged cases. We believe that the complex electronic interactions in these chemical systems, particularly the oxides with spin polarization, limit Finetuna's performance. The long-range magnetic interaction introduces more complexity to the potential energy surface. While this has affected the efficiency of the Finetuna workflow, it also presents opportunities for further exploration. We have established a heuristic criterion to predict the success of a Finetuna run. Specifically, if the maximum force predicted by the ML model exceeds 5 eV Å⁻¹, we recommend using a different initialization strategy, or terminating the simulation and performing DFT calculations instead.

As the accuracy of ML models improves and more material datasets become available, we believe that the Finetuna workflow can be applied to a broader range of chemical systems. We anticipate the rapid emergence of new ML models and look forward to their integration into the workflow. However, to effectively utilize these new models, further research is needed to explore transfer learning strategies and develop fine-tuning techniques specific to the models. The choice of a pre-trained model with suitable architectural features and trained on relevant data can significantly impact the model's performance and generalizability. Investigating out-of-domain detection methods can enhance the robustness of our approach. Additionally, the inclusion of uncertainty quantification in ML models would be valuable, as it could be leveraged as a querying strategy to guide the selection of informative data points for further exploration. These future directions hold promise for advancing the efficiency and accuracy of material discovery applications. The active learning and finetuning approach has the potential to greatly accelerate molecular simulations, leading to the development of more efficient and sustainable materials with a wide range of applications.

The authors acknowledge support from Meta Platforms, Inc. via the Open Catalyst Project collaboration.

The data that support the findings of this study are openly available at the following URL/DOI: https://github.com/ulissigroup/finetuna-2023-manuscript.