Abstract
We present an axiomatic characterization of the Owen–Shapley spatial power index for the case where issues are elements of two-dimensional space. This characterization employs a version of the transfer condition, which enables us to unravel a spatial game into spatial games connected to unanimity games. The other axioms include two conditions concerned particularly with the spatial positions of the players, besides spatial versions of anonymity and dummy. The last condition says that dummy players can be left out in a specific way without changing the power of the other players. We show that this condition can be weakened to requiring dummies to have zero power if we add a condition of positional continuity. We also show that the axioms in our characterization(s) are logically independent.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Voting power in political bodies can be represented by simple games, which identify the winning and losing coalitions: a winning coalition can enforce laws, amendments, etc. In order to measure the power of an individual voter or political party one can use a power index, like for instance the Shapley–Shubik index, which is the Shapley value applied to the transferable utility game that assigns one to winning and zero to losing coalitions. As is well known, the Shapley–Shubik index distributes a total of one among the players by assigning to each player the fraction of the number of player permutations in which that player is pivotal. This way of measuring individual power, however, neither takes the possible issues at stake into account nor the individual positions of the players concerning these issues. In order to remedy this defect, Owen and Shapley (1989), following up on earlier papers of Owen (1971) and Shapley (1977), assume that each player occupies a position in \({\mathbb {R}}^m\): one can think of there being m possible criteria, and a point \(x \in {\mathbb {R}}^m\) represents a position with respect to these criteria. An ‘issue’ is then a function \(f : {\mathbb {R}}^m \rightarrow {\mathbb {R}}\), with the interpretation that if \(f(x) \le f(y)\) then a player with position x is more in favor of issue f, and thus more likely to support f, than a player with position y. Owen and Shapley restrict attention to linear homogenous issues; i.e., an issue can be represented by a vector \(r\in {\mathbb {R}}^m\) with length one, so that a player with position x is more in favor of r than a player with position y if \(r \cdot x \le r \cdot y\) (dot-products). Given a simple game and a constellation of player positions, for each issue r a pivotal player exists, by building a coalition starting with the player whose position has the smallest dot-product with r. Then the Owen–Shapley spatial power index assigns to each player the fraction of issues at which this player is pivotal. In other words, compared to the Shapley–Shubik index, the player permutations are weighted by considering the positions of the players.
Although the model underlying the Owen–Shapley spatial power index may seem somewhat abstract, the concept derives important support from the fact that, at least if \(m=2\) and the simple game is proper and strong (meaning, for each coalition, that either that coalition is winning and its complement losing, or the other way around), the strong point and the center of power coincide. The latter point is the convex combination of the player positions using the Owen–Shapley spatial power index values as weights; and the strong point is the Copeland winner, i.e., the position that is least vulnerable to opposition by (winning) coalitions in terms of Euclidian distance. See Owen and Shapley (1989) for details and a proof of this result.
Another relation between the Owen–Shapley spatial power index and the evaluation of positions using Euclidian distance has recently been obtained by Martin et al. (2014). They show, by using a limit argument, that if pivotalness is based on closeness in terms of Euclidian distance and all possible points in \({\mathbb {R}}^m\) are regarded as ‘issues’, then the Owen–Shapley spatial power index again results. They also clarify the difference and overlap between the original concepts of Owen (1971) and Shapley (1977).
In this paper we assume \(m=2\). A spatial game is a combination of a simple game and a constellation of player positions. A spatial power index assigns to each player in a spatial game a nonnegative number, where these numbers sum up to one. We show that the Owen–Shapley spatial power index is uniquely characterized by five axioms: a version of the well known transfer condition similar to the one in Einy and Haimanko (2011); anonymity and dummy axioms adapted to the spatial context; and two axioms dealing exclusively with the spatial positions of the players. One of these last two axioms requires that it should not matter where the constellation of player positions is located in space: only the players’ relative positions matter. The other axiom says that if the position of one player moves towards the position of another player along the straight line through the two positions, then the power of the latter player does not change. This axiom embodies the fact that such a movement does not change the relative positions of these two players with respect to any issue. Thus, among the five axioms considered it is the one that is most specific for the Owen–Shapley spatial power index; in particular, it reflects the idea of straight lines as representing issues.
Our dummy property has a flavor of consistency: it says that dummies can be left out, in a way to be specified, without changing the power of the other players. In this respect it is related to the Null-Player-Out property in Derks and Haller (1999). A consequence is that our characterization is formulated for a variable player set. We show that by adding a positional continuity condition, the weak dummy property—requiring, as usual, that dummies have zero power—is sufficient, and the player set can be fixed.
We also show that in both characterizations the axioms are logically independent.
As far as we are aware, these are the first characterizations of the Owen–Shapley spatial power index.
Further related literature Far from claiming completeness, we mention a few relevant related papers. Shenoy (1982) provides a spatial version of another well-known power index, the Banzhaf index. Passarelli and Bar (2007) propose a power index which is more directly based on the Euclidian distance of player positions to issues, where the latter are points in the same space as the player positions. They also discuss application to the EU. Benati and Marzetti (2013) take a generalized approach to power indexes, comprising the Shapley–Shubik and Owen–Shapley power indexes, and also apply this to EU’s council of ministers. Blockmans and Guerry (2015), taking the Benati and Marzetti (2013) approach as a lead, introduce issue saliences and consider empirical applications for Belgium. Alonso-Meijide et al. (2011) develop an alternative spatial power index based on lengths of paths connecting player positions and induced by player permutations, and consider an application to the Catalan Parliament.
Also the more specific political science literature provides many interesting references to this topic. We mention in particular Enelow and Hinich (1984, (1990), Grofman et al. (1987), and Straffin (1994) for overviews and applications. For a discussion about the basic underlying assumption of a spatial power index, namely that players (e.g., political parties) are more likely to vote in favor of a particular proposal as their position is closer to the proposal, see Braham and Holler (2005) and Napel and Widgrén (2005). For a general comparison of power indices see Bertini et al. (2013).
Organization of the paper Preliminaries are collected in Sect. 2. Section 3 provides the axioms, main characterization, and logical independence. Section 4 presents the alternative characterization using continuity, and Sect. 5 concludes.
2 Preliminaries
We introduce the relevant notations and concepts in different subsections.
2.1 Notations in \({\mathbb {R}}^2\)
For \(x,y \in {\mathbb {R}}^2\) with \(x \ne y\) we denote by \([x,y,\rightarrow )\) the half-line starting at x and crossing through y. We also use the notation \((\leftarrow ,x,y,\rightarrow )\) for the line through x and y. The line segment with endpoints x and y is denoted by [x, y]; by ]x, y[ we denote the open interval \([x,y]\setminus \{x,y\}\). For \(x \ne y\), the perpendicular bisector of [x, y] is the line through \(\frac{1}{2}x + \frac{1}{2}y\) perpendicular to the line through x and y. For a point x and a line \(\ell \) in \({\mathbb {R}}^2\) such that \(x \notin \ell \) we denote by \(x^\ell \) the reflection of x with respect to \(\ell \), i.e., \(\ell \) is the perpendicular bisector of \([x,x^\ell ]\). For a point \(x \in \ell \) we define \(x^\ell = x\). By \(\bar{x}^\ell \) we denote the projection of a point x on a line \(\ell \), i.e., \(\bar{x}^\ell = \frac{1}{2}x + \frac{1}{2} x^\ell \). For \(x \in {\mathbb {R}}^2\), ||x|| denotes the (Euclidian) length of x. For \(x=(x_1,x_2),\, y=(y_1,y_2) \in {\mathbb {R}}^2\), \(x \cdot y\) denotes the inner product of x and y, i.e., \(x \cdot y = x_1y_1 + x_2y_2\). For a subset \(X \subseteq {\mathbb {R}}^2\), \({ \text{ co } }(X)\) denotes the convex hull of X.
2.2 Simple games
A simple game is a pair (N, v), where N is a nonempty finite subset of \(\mathbb {N}\) and v is a function \(2^N \rightarrow \{0,1\}\) satisfying (a) \(v(\emptyset )=0\) and \(v(N)=1\); and (b) \(v(S) \le v(T)\) for all \(S,T \in 2^N\) with \(S \subseteq T\).Footnote 1 Elements of N are called players and subsets of N coalitions. A coalition S is winning if \(v(S)=1\), otherwise it is losing. A minimal winning coalition is a winning coalition of which each nontrivial subcoalition is losing. We denote by \({\mathcal {V}}^N\) the set of all simple games with player set N.
Player i is pivotal in S if \(v(S)=1\) and \(v(S \setminus \{i\})=0\).
For a simple game (N, v) with at least two players and a player \(i \in N\) we define the game \((N\setminus \{i\},v_{-i})\) as follows: \(v_{-i}(\emptyset )=0\) and \(v_{-i}(S) = v(S \cup \{i\})\) for every \(\emptyset \ne S \subseteq N \setminus \{i\}\). The game \((N\setminus \{i\},v_{-i})\) can be interpreted as player i withdrawing from (N, v) but leaving his ‘consent’ behind; in particular, a winning coalition in (N, v) remains winning in \((N\setminus \{i\},v_{-i})\), i.e., also without player i. Note that, indeed, \((N\setminus \{i\},v_{-i}) \in {\mathcal {V}}^{N\setminus \{i\}}\).Footnote 2
2.3 Constellations
A constellation for player set N is a vector \(p=(p_i)_{i\in N} \in ({\mathbb {R}}^2)^N\) such that \(p_i \ne p_j\) for all \(i,j \in N\) with \(i \ne j\). We denote by \({\mathcal {P}}^N\) the set of all constellations for player set N. For \(p \in {\mathcal {P}}^N\) and \(i\in N\), \(p_{-i} \in {\mathcal {P}}^{N \setminus \{i\}}\) is defined by \((p_{-i})_j = p_j\) for every \(j \in N\setminus \{i\}\). For a line \(\ell \) in \({\mathbb {R}}^2\) and \(p \in {\mathcal {P}}^N\), we denote \(p^\ell = (p_i^\ell )_{i\in N}\). Hence, the constellation \(p^\ell \) is the reflection of the constellation p with respect to \(\ell \).
2.4 Spatial games
A spatial game for player set N is a triple (N, v, p) where \((N,v) \in {\mathcal {V}}^N\) and \(p \in {\mathcal {P}}^N\).
Player i is a dummy in (N, v, p) if \(p_i \in { \text{ co } }(\{p_j \mid j \in S \setminus \{i\}\})\) for every coalition S in which i is pivotal. Note that, in particular, a player who is pivotal in no coalition in the simple game (N, v), is a dummy. More generally, a dummy i, even if he is pivotal in some coalition S, does not occupy an ‘extreme’ position in that coalition and therefore will (almost) never exploit this pivotalness: whatever the issue, player i will not be the last player of coalition S to consent. This interpretation is clearly consistent with the idea underlying the Owen–Shapley spatial power index, but it is also consistent with alternative approaches as mentioned in the introduction. For instance, if issues are identified with points in \({\mathbb {R}}^2\) and we take the Euclidian distance as a measure of being close to an issue, then in the situation above player i will never have maximal distance to an issue within the coalition S, and thus will never be the last player in S to consent.
2.5 Power indices
A spatial power index is a function \(\varphi \) which maps each spatial game (N, v, p) to a vector \(\varphi (N,v,p) \in {\mathbb {R}}^N\), such that \(\varphi _i(N,v,p) \ge 0\) for all \(i\in N\) and \(\sum _{i\in N} \varphi _i(N,v,p)=1\).Footnote 3 Note, in particular, that a spatial power index is, thus, defined for every (finite) player set \(N \subseteq \mathbb {N}\).
Central in this paper is the Owen–Shapley spatial power index (Owen and Shapley 1989), which we define next.
Let (N, v, p) be a spatial game and let \(U = \{ r \in {\mathbb {R}}^2 \mid ||r||=1\}\) denote the circle with radius 1. We say that player \(i \in N\) is pivotal at \(r \in U\) if i is pivotal in \(S = \{ j\in N \mid r\cdot p_j \le r \cdot p_i\}\). Then at each \(r\in U\), except at at most finitely many points, there is a unique pivotal player. Let \(\rho _i\) be the total length of the arc(s) of U where player i is pivotal, divided by \(2\pi \) (the total length of U); so \(\sum _{i \in N} \rho _i = 1\). Alternatively, \(\rho _i\) is the probability that player i is pivotal if r is chosen from the uniform distribution over U. The Owen–Shapley spatial power index \(\Phi \) now assigns these probabilities to the spatial game (N, v, p): \(\Phi (N,v,p) = (\rho _i)_{i \in N}\).
From a geometric point of view—which we will use often in the sequel—player i is pivotal at r if the following holds. Consider a(ny) line \(\ell \) in \({\mathbb {R}}^2\) parallel to r, and the projections \(\bar{p}_j^\ell \) of the points \(p_j\), \(j\in N\), on \(\ell \). Say that player j precedes player i on \(\ell \) if the projection \(\bar{p}^\ell _j\) (weakly) precedes \(\bar{p}^\ell _i\) when going along \(\ell \) in the direction of r. If player i is pivotal in the set of preceding players (which includes himself), then i is pivotal at r.Footnote 4
To further illustrate the Owen–Shapley spatial power index, we compute it for the case in which the game v is a unanimity game.
Example 2.1
We compute \(\Phi \) for the spatial game \((N,u_T,p)\) where \(\emptyset \ne T \subseteq N\) and \(u_T\) is the unanimity game on T, i.e., \(u_T(S)=1\) if \(T \subseteq S\) and \(u_T(S)=0\) otherwise. The players outside T are, trivially, dummies and, in particular, cannot be pivotal at any \(r\in U\). Hence, \(\Phi _i(N,u_T,p)=0\) for all \(i \in N \setminus T\) and moreover the points \(p_i\) for those players play no role in determining \(\Phi _j(N,u_T,p)\) for the players j in T. If \(p_j \in { \text{ co } }(\{p_i \mid i \in T \setminus \{j\}\})\) for some \(j \in T\), then again j is a dummy in \((N,u_T,p)\), and for any line \(\ell \) the projection \(\bar{p}_j^\ell \) is located between projections of other players in T, so that j can be pivotal at at most finitely many r; hence \(\Phi _j(N,u_T,p) = 0\). Let \(T'\) consist of the remaining (non-dummy) players in T, and let \(P={ \text{ co } }(\{p_i \mid i \in T'\})\). Thus, \(p_i\) is an extreme point of P for every \(i \in T'\). Without loss of generality suppose that \(P=\{p_1,\ldots ,p_k\}\) and that the point \(p_i\) is adjacent to \(p_{i-1}\) and \(p_{i+1}\) for each \(i \in T'\), where \(p_0=p_k\) and \(p_{k+1}=p_1\). For each \(i \in T'\) let \(\alpha _i\) denote the angle (in radians) at \(p_i\) in P.
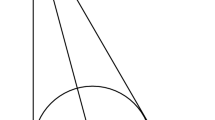
Illustrating Example 2.1
Let \(i \in T'\). We compute \(\Phi _i(N,u_T,p)\). Clearly, if \(k=1\) then \(\Phi _i(N,u_T,p)=1\). Now assume that \(k \ge 2\). Let \(\ell \) be the line through \(p_{i-1}\) and \(p_i\) and let m be the line through \(p_{i+1}\) and \(p_i\) (see Fig. 1). Let \(\ell ^\bot \) be the line through \(p_i\) perpendicular to \(\ell \) and let \(m^\bot \) be the line through \(p_i\) perpendicular to m.Footnote 5 Consider a vector r of length one starting at \(p_i\). Then the projections of the points \(p_j\) for \(j \in T'\) precede the projection of \(p_i\) on the line through \(p_i\) in the direction of r if and only if r is in between \(\ell ^\bot \) and \(m^\bot \) and pointing outward from P. It is easy to see that the (outward) angle between \(\ell ^\bot \) and \(m^\bot \) is equal to \(\pi - \alpha _i\), so that \(\Phi _i(N,u_T,p) = (\pi - \alpha _i)/2\pi \). Since the sum of the angles at the vertices of P is equal to \((k-2)\pi \) we have, indeed,
Figure 2 illustrates the Owen–Shapley spatial power index when the simple game is a three-person unanimity game \((\{1,2,3\},u_{\{1,2,3\}},(p_1,p_2,p_3))\). By moving the center of the triangle and the dashed lines to (for instance) \(p_3\), we obtain a similar situation as in Fig. 1.
3 An axiomatic characterization of the Owen–Shapley spatial power index
We formulate the axioms and state and prove the main characterization result. We also show that the axioms are independent.
3.1 The axioms
Throughout, let \(\varphi \) be a power index. The first axiom is equivalent to the well-known transfer axiom of Dubey (1975), as remarked in Dubey et al. (2005). Here we use a different name which reflects its content in a more direct manner.
Equal Power Change (EPC) For all player sets N, all \(p \in {\mathcal {P}}^N\), and all \(v,v',w,w' \in {\mathcal {V}}^N\), if \(v - v' = w - w' \ge 0\), then \(\varphi (N,v,p)-\varphi (N,v',p) = \varphi (N,w,p)-\varphi (N,w',p)\).
EPC says that, for each constellation, if the same winning coalitions are added when going from \(v'\) to v as when going from \(w'\) to w, then the change in power for every player when going from \(v'\) to v should be equal to the change in power when going from \(w'\) to w. As in Einy and Haimanko (2011), the condition will imply that, for each fixed constellation, the power index for arbitrary simple games is completely determined by its value on unanimity games as in Example 2.1.
The second axiom requires that dummies can be left out—while leaving behind their consent—without any effect on the power of the remaining players.
Dummy Property (DP) For every spatial game (N, v, p) and every dummy i in (N, v, p), \(\varphi _j(N,v,p) = \varphi _j(N\setminus \{i\},v_{-i},p_{-i})\) for every \(j \in N\setminus \{i\}\).
The Dummy Property is in line with the definition and interpretation of a dummy in Sect. 2.4. It is similar in spirit to the Null-Player-Out property of Derks and Haller (1999), in that it requires that dummies not only have zero power (which is a direct consequence of DP) but can be left out, in the way specified, without changing the power of the remaining players. In Sect. 3.3 we demonstrate that it is not sufficient to require only that dummies have zero power, and in Sect. 4 we show that this does suffice when we add a continuity condition.
The third axiom is a standard anonymity requirement, expressing that it should not matter how the players in a spatial game are called. Let \(N \subseteq \mathbb {N}\) be finite and let \(\sigma : N \rightarrow \mathbb {N}\) be an injective function. For a spatial game (N, v, p) define the spatial game \((\sigma (N),\sigma v, \sigma p)\) by \(\sigma v(\sigma (S)) = v(S)\) for all \(S \subseteq N\) and \((\sigma p)_{\sigma (i)} = p_i\) for all \(i \in N\).
Anonymity (AN) For every spatial game (N, v, p) and every injective function \(\sigma : N \rightarrow \mathbb {N}\), \(\varphi _{\sigma (i)}(\sigma (N),\sigma v, \sigma p) = \varphi _i(N,v,p)\) for all \(i \in N\).
The last two axioms concern constellations. The first implies that it does not matter where in \({\mathbb {R}}^2\) the constellation is located. It is a natural consequence of the assumption that for a power index all potential issues are taken into consideration and are regarded equally likely, so that only the relative positions of the players matter. In other words, the choice of the origin and of the two axes in two-dimensional Euclidian space should not influence the power of the players. Without this condition, other distributions of issues than the uniform one become possible (cf. Sect. 3.3). We formulate the axiom by requiring that the power of the players does not change if we reflect the constellation with respect to any straight line. Note that by such reflections, we can shift and rotate the whole constellation to any desired position.
Reflection Invariance (RI) For every spatial game (N, v, p) and every line \(\ell \) in \({\mathbb {R}}^2\), \(\varphi (N,v,p) = \varphi (N,v,p^\ell )\).
The final axiom reflects the consideration that what matters in a constellation are the relative positions of the players as expressed by the lines connecting them. Specifically, the axiom states that the power of a player i does not change if the position \(p_j\) of another player j moves along the line through \(p_i\) and \(p_j\) without passing \(p_i\). Note that this implies that the order of precedence of the projections of \(p_i\) and \(p_j\) on any line does not change.
As an example, think of an issue as representing the amount of increase of public spending on social security versus the amount of increase of public spending on national defense, and suppose that party j wants to increase spending (measured in some unit) by 30 and 10, respectively, while party i wants to increase spending by 45 and 15. Hence, the parties agree that three times as much should be spent more on social security than on national defense, but they disagree on the amounts. On this issue, as far as coalition formation is concerned and starting from some low amounts, party j would enter a coalition before party i, and this does not change if, for instance, j changes its preferred amounts to 42 and 14. Similarly, the order of precedence does not change on any other issue (for instance, decrease with equal amounts) if we take the projections (points with minimal Euclidian distance) of the 3:1-issue positions as the parties’ positions with respect to that issue. The axiom below is going to require that in this case party i’s power does not change. It says nothing about party j, since the position of j with respect to parties other than i will have changed in general.
As a simpler, one-dimensional example, suppose there is a moderate left party, a centre party, and a moderate right party, and suppose that the moderate right party changes to extreme right. The axiom we are going to state requires that the power of each party is the same in the old and in the new situation, since the relative positions of the parties have not changed.
Thus, while all five axioms will be crucial for obtaining the Owen–Shapley spatial power index—see Sect. 3.3—this final axiom most closely reflects the ideas underlying this index. In this sense, the reasonableness of the axiom is intimately related to the reasonableness of the model underlying the Owen–Shapley spatial power index.
Positional Invariance (PI) For all player sets N, \(i \in N\), and \(p,p' \in {\mathcal {P}}^N\), if \(p'_i=p_i\) and \(p'_j \in [p_i, p_j, \rightarrow )\) for all \(j \in N \setminus \{i\}\), then \(\varphi _i(N,v,p) = \varphi _i(N,v,p')\) for all \((N,v) \in {\mathcal {V}}^N\).
Positional Invariance indeed confirms that issues are identified with lines: if position \(p_j\) moves along the line through \(p_i\) and \(p_j\) in the direction of \(p_i\) or away from \(p_i\), then the relative positions of i and j with respect to the issue represented by that line or by any other line do not change.
3.2 The characterization
The main result of this paper is the following.
Theorem 3.1
The Owen–Shapley spatial power index \(\Phi \) is the unique spatial power index satisfying EPC, DP, AN, RI, and PI.
We first show that \(\Phi \) satisfies the five axioms in the theorem.
Lemma 3.2
\(\Phi \) satisfies EPC.
Proof
To show that \(\Phi \) satisfies EPC, let \(p\in {\mathcal {P}}^N\) and let \(v,v',w,w'\) be simple games with player set N, satisfying \(v-v' = w-w' \ge 0\). Write \(n=|N|\). It is sufficient to consider the case where v arises from \(v'\) and w from \(w'\) by adding the minimal winning coalition S. First consider a player \(i \in S\). Then \(v(T\cup \{i\})-v(T) \ge v'(T\cup \{i\})-v'(T)\) and \(w(T\cup \{i\})-w(T) \ge w'(T\cup \{i\})-w'(T)\) for all \(T \subseteq N\setminus \{i\}\). This implies that, according to \(\Phi \), player i can never lose power when going from \(v'\) to v and from \(w'\) to w. Player i gains, when going from \(v'\) to v, at an \(r\in U\) where he is not pivotal according to \(v'\) but pivotal according to v. Suppose the induced ordering at such an r is \(i_1,\ldots ,i_n\), player \(i_t\) is pivotal according to \(v'\), \(S \subseteq \{i_1,\ldots ,i_{t-1}\}\), and i is the last player of S in this ordering, say \(i=i_s\) for some \(s \le t-1\). Then \(\{i_1,\ldots ,i_s\}\) is losing in \(v'\) and winning in v, and therefore losing in \(w'\) and winning in w. Also, \(\{i_1,\ldots ,i_{s-1}\}\) is losing in \(v'\), v, \(w'\), and therefore also in w. Thus, player i is pivotal according to v and according to w but not according to \(v'\) and \(w'\). Hence, the gain in power for player i at this particular ordering when going from \(v'\) to v and when going from \(w'\) to w is equal to the share of the vectors \(r\in U\) inducing this ordering, which depends exclusively on the constellation p. We conclude that the gain of each player \(i \in S\) when going from \(v'\) to v and when going from \(w'\) to w is the same.
Next, let \(i \notin S\). Now player i can only lose when going from \(v'\) to v and from \(w'\) to w. Player i loses, when going from \(v'\) to v, at an \(r\in U\) where he is pivotal according to \(v'\) but not pivotal according to v. Suppose the induced ordering at such an r is \(i_1,\ldots ,i_n\), player \(i=i_t\) is pivotal according to \(v'\), and \(S \subseteq \{i_1,\ldots ,i_{t-1}\}\), so that player i is no longer pivotal according to v. Since S is also winning in w, player i is also not pivotal according to w. Since \(\{i_1,\ldots ,i_{t-1}\}\) is losing in \(v'\) and winning in v, it must be losing in \(w'\); and since \(\{i_1,\ldots ,i_t\}\) is winning in \(v'\), v, and w, it must be winning in \(w'\). Hence, player i is pivotal according to \(w'\). Hence, the loss in power for player i at this particular ordering when going from \(v'\) to v and when going from \(w'\) to w is equal to the share of the vectors \(r\in U\) inducing this ordering, which depends exclusively on the constellation p. We conclude that the loss of each player \(i \notin S\) when going from \(v'\) to v and when going from \(w'\) to w is the same. \(\square \)
Lemma 3.3
\(\Phi \) satisfies DP, AN, RI, and PI.
Proof
Let (N, v, p) be a spatial game. If player i is a dummy, i.e., \(p_i \in { \text{ co } }(\{p_j \mid j \in S \setminus \{i\}\})\) for every coalition S in which i is pivotal, then the projection of \(p_i\) on any line \(\ell \) is in between the projections of other players in S, for every S in which i is pivotal. Hence, player i is pivotal at at most finitely many \(r\in U\). Thus, \(\Phi _i(N,v,p)=0\) and nothing changes for the other players if we leave out player i from (N, v) and \(p_i\) from p, i.e., \(\varphi _j(N,v,p) = \varphi _j(N\setminus \{i\},v_{-i},p_{-i})\) for every \(j \in N\setminus \{i\}\). Hence, \(\Phi \) satisfies DP.
AN of \(\Phi \) is obvious by definition. For RI, suppose that player i in (N, v, p) is pivotal at some \(r\in U\). Let \(\ell \) be a line in \({\mathbb {R}}^2\), and let m be the line through the origin parallel to \(\ell \). Then it is easy to check that player i is pivotal at \(r^m \in U\) in the spatial game \((N,v,p^\ell )\). Since this holds for every player i and every \(r \in U\), RI of \(\Phi \) follows.
Finally, let \(p'\in {\mathcal {P}}^N\) and \(i\in N\) such that \(p'_i=p_i\) and \(p'_j \in [p_i, p_j, \rightarrow )\) for all \(j \in N \setminus \{i\}\). Then, for every \(r \in U\), player i is pivotal at r in (N, v, p) if and only if he is pivotal at r in \((N,v,p')\), since the set of preceding players of player i does not change. Therefore, \(\varphi _i(N,v,p) = \varphi _i(N,v,p')\), and PI of \(\Phi \) is proved. \(\square \)
Lemmas 3.2 and 3.3 imply that the Owen–Shapley spatial power index satisfies the five axioms in the theorem. We now show uniqueness.
The next lemma implies that, if \(\varphi \) satisfies EPC, then it is completely determined by its value on unanimity games as defined in Example 2.1. The lemma follows from Lemma 2.3 in Einy (1987), see also Einy and Haimanko (2011).
Lemma 3.4
Let \(\varphi \) be a spatial power index satisfying EPC and let (N, v, p) be a spatial game. Let \(T_1,\ldots ,T_k\) be the minimal winning coalitions in (N, v). Then
Until further notice, \(\varphi \) is a spatial power index satisfying DP, AN, RI, and PI.
For a spatial game \((N,u_T,p)\), let \(T_p \subseteq T\) denote the set of non-dummies.
Lemma 3.5
Let \((N,u_T,p)\) be a spatial game, where \(\emptyset \ne T \subseteq N\). Then \(\varphi _i(N,v,p)=0\) for all \(i \in N \setminus T_p\) and \(\varphi _i(N,u_T,p) = \varphi _i(T_p,u_{T_p},p')\) for all \(i\in T_p\), where \(p'\) is the restriction of p to \(T_p\).
Proof
Let \(j \in N \setminus T_p\), then \(\varphi _i(N,u_T,p) = \varphi _i(N \setminus \{j\}, (u_T)_{-j},p_{-j})\) for all \(i \in N \setminus \{j\}\) by DP. In particular, \(\varphi _j(N,v,p)=1 - \sum _{i\in N \setminus \{j\}} \varphi _i(N \setminus \{j\}, (u_T)_{-j},p_{-j}) = 1-1 =0\); and \(\varphi _i(N,u_T,p) = \varphi _i(N \setminus \{j\}, u_{T\setminus \{j\}}, p_{-j})\) for all \(i \in N \setminus \{j\}\). Also, \(T_p\) is still the set of non-dummies in \((N \setminus \{j\}, u_{T\setminus \{j\}}, p_{-j})\). The lemma now follows from repeated application of this argument. \(\square \)
In view of Lemma 3.5 we may restrict attention to spatial games of the form \((N,u_N,p)\) and having no dummies. The next lemma establishes a very useful consequence of AN and RI for this kind of spatial game.
Lemma 3.6
Let \((N,u_N,p)\) be a spatial game and suppose that for two distinct players i and j with \(\ell \) the perpendicular bisector of \([p_i,p_j]\) we have \(\{p_k^\ell \mid k \in N \} = \{ p_k \mid k \in N\}\). Then \(\varphi _i(N,u_N,p)=\varphi _j(N,u_N,p)\).
Proof
Consider \(\sigma : N \rightarrow N\) defined by \(\sigma (k) = k'\) if \(p_{k'}=p_k^\ell \). By AN, \(\varphi _i(N,u_N,p) = \varphi _{\sigma (i)}(N, \sigma u_N, \sigma p)= \varphi _j(N,u_N,p^\ell )\). By RI, \(\varphi _j(N,u_N,p^\ell ) = \varphi _j(N,u_N,p)\). Hence \(\varphi _i(N,u_N,p)=\varphi _j(N,u_N,p)\). \(\square \)
Next we take care of spatial games with one or two players.
Lemma 3.7
Let \((N,u_N,p)\) be a spatial game. If \(|N|=1\) or \(|N|=2\) then \(\varphi (N,u_N,p) = \Phi (N,u_N,p)\).
Proof
Observe that in both cases there are no dummies. If \(N = \{i\}\) then clearly \(\varphi _i(N,u_N,p) = \Phi _i(N,u_N,p)=1\). If \(N=\{i,j\}\) with \(j \ne i\) then \( \varphi _i(N,u_N,p)= \varphi _j(N,u_N,p)\) by Lemma 3.6. This holds also for \(\Phi \), and we obtain \(\Phi _i(N,u_N,p)=\Phi _j(N,u_N,p)=\varphi _i(N,u_N,p)=\varphi _j(N,u_N,p)= \frac{1}{2}\). \(\square \)
The main part of the proof consists of the three-player case, starting with the following lemma.
Lemma 3.8
Let \(|N|=3\), \(k\in N\), \(p\in {\mathcal {P}}^N\), and let co \((\{p_i \mid i \in N\})\) have a right angle at \(p_k\). Then \(\varphi _k(N,u_N,p)=\Phi _k(N,u_N,p)=\frac{1}{4}\).
Illustrating the proof of Lemma 3.8
Proof
(cf. Fig. 3) Without loss of generality let \(N=\{1,2,3\}\) with \(k=2\) and consider an additional player 4 with \(p_4\in {\mathbb {R}}^2\) such that \({ \text{ co } }(\{p_i \mid i\in N \cup \{4\} \})\) is a rectangle with vertex \(p_4\) opposite of \(p_2\). Consider the spatial game \((N\cup \{4\},\) \(u_{N \cup \{4\}},p)\). By Lemma 3.6 we obtain \(\varphi _1(N \cup \{4\}, u_{N \cup \{4\}},p) = \varphi _2(N \cup \{4\}, u_{N \cup \{4\}},p)\), and similarly \(\varphi _2(N \cup \{4\}, u_{N \cup \{4\}},p) = \varphi _3(N \cup \{4\}, u_{N \cup \{4\}},p) = \varphi _4(N \cup \{4\}, u_{N \cup \{4\}},p)\), so that \(\varphi _i(N \cup \{4\},u_{N \cup \{4\}},p) = \frac{1}{4}\) for every \(i=1,\ldots ,4\).
Next consider the spatial game \((N\cup \{4\},u_{N \cup \{4\}},q)\), where \(q_i=p_i\) for \(i=1,2,3\) and \(q_4 = \frac{1}{2}p_1 + \frac{1}{2}p_3\). By PI, \(\varphi _2 (N \cup \{4\},u_{N \cup \{4\}},q) = \varphi _2 (N \cup \{4\},u_{N \cup \{4\}},p) = \frac{1}{4}\). Since player 4 is a dummy in \((N \cup \{4\},u_{N \cup \{4\}},q)\), we obtain \(\varphi _2(N,u_N,p) = \varphi _2(N,(u_{N\cup \{4\}})_{-4},q_{-4}) = \varphi _2 (N \cup \{4\}, u_{N \cup \{4\}},q) = \frac{1}{4}\), where the second equality follows from DP. The same argument (or Example 2.1) applies to \(\Phi \). \(\square \)
In what follows we use the notation \(\measuredangle \,xyz\) for the size of the (smaller) angle, measured in radians, at y between the line through x and y and the line through z and y. The following lemma and its proof are illustrated in Fig. 4.
Illustrating Lemma 3.9 and its proof
Lemma 3.9
Let a, b, c, and d be four distinct points in \({\mathbb {R}}^2\) such that b and c are on different sides of the line through a and d, and \(\measuredangle \,bad + \measuredangle \,cad < \pi \). Let \(N = \{i,j,k\}\), \(|N|=3\), and let \(p,q,s \in {\mathcal {P}}^N\) be defined by \(p = (p_i,p_j,p_k) = (a,b,c)\), \(q = (q_i,q_j,q_k) = (a,b,d)\), and \(s = (s_i,s_j,s_k) = (a,d,c)\), Then
If, additionally, \(\measuredangle \,bad = \measuredangle \,cad\), then
Proof
Take a point x in the open line segment between a and d, such that the line through x perpendicular to the line through a and d intersects the open line segment between a and b in a point y and the open line segment between a and c in a point z. By PI it is sufficient to prove that
and if \(\measuredangle \,bad = \measuredangle \,cad\),
where \(\widetilde{p}=(\widetilde{p}_i,\widetilde{p}_j,\widetilde{p}_k)=(a,y,z)\), \(\widetilde{q}=(\widetilde{q}_i,\widetilde{q}_j,\widetilde{q}_k)=(a,y,x)\), and \(\widetilde{s}=(\widetilde{s}_i,\widetilde{s}_j,\widetilde{s}_k)=(a,x,z)\). Now
where the first equality follows from PI and the second from Lemma 3.8. By analogous arguments,
Combining (1) and (2) we obtain
which completes the proof of the first statement. Now suppose, additionally, that \(\measuredangle \,bad = \measuredangle \,cad\). Then by Lemma 3.6 we have \(\varphi _j(N,u_N,\widetilde{p}) = \varphi _k(N,u_N,\widetilde{p})\). By (1) and (2) this implies \(\varphi _i(N,u_N,\widetilde{q}) = \varphi _i(N,u_N,\widetilde{s})\), and the second statement in the lemma follows. \(\square \)
Lemma 3.10
Let \(N=\{i,j,k\}\), \(|N|=3\), and let \(p \in {\mathcal {P}}^N\) such that \(\measuredangle \,p_j p_i p_k = \frac{m}{2^h}\pi \) for some \(h,m \in \mathbb {N}\) with \(m < 2^h\). Then \(\varphi _i(N,u_N,p) = \frac{1}{2}-\frac{m}{2^{h+1}}\).
Proof
First suppose \(m=1\). If \(h=1\) then \(\varphi _i(N,u_N,p) = \frac{1}{4}\) by Lemma 3.8. Assume that the statement has been proved for h, then for \(h+1\) we have by the second statement in Lemma 3.9 that
hence \(\varphi _i(N,u_N,p) = \frac{1}{2} - \frac{1}{2^{h+2}}\). By induction the statement in the lemma follows for \(m=1\) and all \(h \in \mathbb {N}\). Now suppose the statement in the lemma has been proved for m and arbitrary h such that \(m+1 < 2^h\), Then by the first statement in Lemma 3.9 we obtain for \(m+1\)
and the proof of the lemma is complete by induction. \(\square \)
Let
With some abuse of notation we will write \(\varphi (\alpha ) := \varphi _i(N,u_N,p)\) for \((N,u_N,p)\) as in Lemma 3.10, where \(\alpha = \measuredangle \,p_j p_i p_k \in A\). Observe that A is a dense subset of the interval \((0,\pi )\) and that \(\varphi : A \rightarrow (0,\frac{1}{2})\), \(\frac{m}{2^h}\pi \mapsto \frac{1}{2}-\frac{m}{2^{h+1}}\) is a decreasing continuous function. Note that \(\varphi (\alpha ) = \frac{\pi -\alpha }{2\pi }\) for every \(\alpha \in A\).
Next, we extend these findings to all of \((0,\pi )\).
Lemma 3.11
Let a, b, c, and d be four distinct points in \({\mathbb {R}}^2\) such that d and b are on different sides of the line through a and c, and \(0< \measuredangle \,cab< \measuredangle \,dab < \pi \). Let \(N=\{i,j,k\}\), \(|N|=3\), let \(p = (p_i,p_j,p_k) = (a,b,c)\) and let \(q = (q_i,q_j,q_k) = (a,b,d)\). Then \(\varphi _i(N,u_N,p) \ge \varphi _i(N,u_N,q)\).
Illustrating the proof of Lemma 3.11
Proof
By PI we may assume that the line m through b and d is perpendicular to the line \(\ell \) through a and c and that these two lines intersect in c. See Fig. 5 for an illustration of this and of the later part of the proof. Without loss of generality we assume \(i=1\), \(j=2\), \(k=3\).
Consider the spatial game \((N \cup \{4\},u_{N\cup \{4\}},(a,b,e,d))\), where \(e = a^m\). By PI and DP we obtain
which can be seen by moving the location d of player 4 to c along m. Since \(\varphi _1(N,u_{N},\) (a, b, e)) \(= \varphi _3(N,u_{N},(a,b,e))\) by Lemma 3.6, we have
Since also \(\varphi _1(N\cup \{4\},u_{N\cup \{4\}},(a,b,e,d)) = \varphi _3(N\cup \{4\},u_{N\cup \{4\}},(a,b,e,d))\) by Lemma 3.6, we obtain
Combining (3)–(5) and the assumption that \(\varphi _4(N\cup \{4\},u_{N\cup \{4\}},(a,b,e,d)) \ge 0\), we obtain
By PI, \(\varphi _1(N,u_{N},(a,b,e)) = \varphi _1(N,u_{N},(a,b,c))\) and by PI and DP, \(\varphi _1(N\cup \{4\},u_{N\cup \{4\}},(a,b,e,d)) = \varphi _1(\{1,2,4\},u_{\{1,2,4\}},(a,b,d)\). Together with (6) we have \(\varphi _1(N,u_N,(a,b,c)) \ge \varphi _1(\{1,2,4\},u_{\{1,2,4\}},(a,b,d)\), hence by AN, \(\varphi _1(N,\) \(u_N,(a,b,c)) \ge \varphi _1(N,u_N,(a,b,d)\). \(\square \)
Lemma 3.11 in fact states that in a spatial game \((N,u_N,p)\) with three players and the points \(p_k\) forming a triangle, the power of player i decreases as the angle at the point \(p_i\) increases. Combined with Lemma 3.10 and the discussion following it we thus obtain the following result.
Corollary 3.12
Let \(N=\{i,j,k\}\), \(|N|=3\), and let \(p \in {\mathcal {P}}^N\). Then for each \(i \in N\),
The case with an arbitrary number of players now follows easily.
Corollary 3.13
Let \((N,u_N,p)\) be a spatial game without dummies and let \(i,j,k \in N\) such that \(p_j\) and \(p_k\) are adjacent to \(p_i\). Then
Proof
By shifting the position of every player in \(N\setminus \{i,j,k\}\) inside the triangle with vertices \(p_i\), \(p_j\), and \(p_k\) along the straight line through \(p_i\), we obtain by PI and DP that \(\varphi _i(N,u_N,p) = \varphi _i(\{i,j,k\},u_{\{i,j,k\}},(p_i,p_j,p_k))\). The claim now follows from Corollary 3.12. \(\square \)
Proof of Theorem 3.1
By Lemmas 3.2 and 3.3, \(\Phi \) satisfies all the axioms in the theorem. The converse follows from Corollary 3.13 and Lemma 3.5, combined with Lemma 3.4. \(\square \)
3.3 Independence of the axioms
The following spatial power indices show that the axioms in Theorem 3.1 are logically independent.
(1) Define
for every spatial game (N, v, p), where \(T_1,\ldots ,T_k\) are the minimal winning coalitions in (N, v) (cf. Lemma 3.4). Then \(\varphi ^1\) satisfies all the axioms in Theorem 3.1 except EPC.
(2) Define \(\varphi ^2_i(N,v,p)=1/|N|\) for every spatial game (N, v, p) and every \(i \in N\). Then \(\varphi ^2\) satisfies all the axioms in Theorem 3.1 except DP.
(3) Let \(\alpha _i\), \(i\in \mathbb {N}\), be positive real numbers, not all equal, and let \(\varphi ^3_i(N,v,p)=\alpha _i \Phi _i(N,v,p)/\sum _{j\in N} \alpha _j \Phi _j(N,v,p)\) for every spatial game (N, v, p) and every \(i \in N\). Then \(\varphi ^3\) satisfies all the axioms in Theorem 3.1 except AN.
(4) Take an arbitrary non-uniform density g over the unit circle U. For a spatial game (N, v, p) and every player \(i \in N\), let \(U_i\) be the subset of U consisting of all \(r \in U\) at which player i is pivotal, and let \(\varphi ^4_i(N,v,p) = \int _{r\in U_i} g(r)dr\). Then \(\varphi ^4\) satisfies all the axioms in Theorem 3.1 except RI.
(5) For a spatial game (N, v, p), player \(i\in N\), and \(r\in U\), call i d-pivotal at r if i is pivotal in \(S = \{j \in N \mid ||p_j-r|| \le ||p_i-r||\}\). Let \(D_i\) be the subset of U consisting of all \(r \in U\) at which player i is d-pivotal, and let \(\varphi ^5_i(N,v,p) = \int _{r\in D_i} u(r)dr\), where u is the uniform density over U. Then \(\varphi ^5\) satisfies all the axioms in Theorem 3.1 except PI.
Remark 3.14
We show that also the (implicit) nonnegativity requirement on a spatial power index cannot be dispensed with. Recall that this condition is (only) used in the proof of Lemma 3.11, which shows that the power of a player i decreases if the angle at the extreme point \(p_i\) of the polytope of the player positions increases. Without Lemma 3.11 we still have that \(\varphi _i(N,u_N,p) = \frac{1}{2}(1-q)\) for a spatial game \((N,u_N,p)\) without dummies, if the angle at \(p_i\) is equal to \(q\pi \) for some \(q = m /2^h\), \(h,m\in \mathbb {N}\), \(m<2^h\). We will now define a power index which still satisfies this property and all axioms in Theorem 3.1, with sum of the powers of the players equal to one, but which violates nonnegativity. To this end, let \(g : {\mathbb {R}} \rightarrow {\mathbb {R}}\) be an additive function (i.e., \(g(x+y)=g(x)+g(y)\) for all \(x,y \in {\mathbb {R}}\)) such that \(g(x)=x\) for all \(x \in \mathbb {Q}\) but not for all \(x \in {\mathbb {R}}\).Footnote 6 We construct a spatial power index \(\psi \) by defining it for all \((N,u_N,p)\), \(N \subseteq \mathbb {N}\), such that no player \(i \in N\) is a dummy. By DP and EPC, \(\psi \) is then extended to all spatial games. Let \((N,u_N,p)\) be a spatial game without dummies. Let the angle at \(p_i\), \(i\in N\), be \(x_i\pi \). Then we define \(\psi _i(N,u_N,p) = \frac{1}{2}(1-g(x_i))\) for all \(i\in N\). Since \(\psi \) depends only on the angles in the polytope determined by the constellation p, it follows that \(\psi \) satisfies AN, RI, and PI. Also, \(\sum _{i\in N} \psi _i(N,u_N,p) = \frac{1}{2}(|N| - g(\sum _{i\in N} x_i)) = \frac{1}{2}(|N| - (|N|-2)) = 1\), where the first equality follows from additivity of g. Since \(g(x) \ne x\) for some \(x\in {\mathbb {R}}\), it follows that \(\psi \ne \Phi \). Consequently, nonnegativity must be violated.
Remark 3.15
The usual dummy condition would only require that dummy players obtain zero. We now show that this condition would not be sufficient to characterize the Owen–Shapley spatial power index. For a spatial game (N, v, p), let \(N_p(v,p)\) denote the set of non-dummies. Define the power index \(\psi \) as follows: for every spatial game (N, v, p) with \(|N| \ne 3\), let \(\psi (N,v,p) = \Phi (N,v,p)\). If \(|N|=3\), let \(\psi _i(N,v,p) = 1/|N_p(v,p)|\) if \(i \in N_p(v,p)\) and let \(\psi _i(N,v,p) = 0\) if \(i \notin N_p(v,p)\). The spatial power index \(\psi \) satisfies EPC, AN, RI, and PI, but not DP; however, it satisfies the weaker requirement that dummies obtain zero. Observe that, for \(|N|=3\), \(\psi \) is not continuous in the constellation \(p\,\): if none of the players is a dummy but one of the positions converges to a dummy position then the associated power remains at \(\frac{1}{3}\) and thus does not converge to zero.
4 Weak dummy and continuity
In this section we fix the player set N, and the power index \(\varphi \) is defined for all spatial games with this fixed player set, i.e., each pair (v, p), such that (N, v) is a simple game and p is a constellation for N. The axioms EPC, RI and PI are as before, but restricted to spatial games with player set N. In the formulation of the anonymity axiom, \(\sigma \) is now a permutation of N. We weaken DP as follows.
Weak Dummy Property (WDP) For every spatial game (v, p) and every dummy i in (v, p), \(\varphi _i(v,p) = 0\).
We will impose the following continuity condition.
Positional Continuity (PC) For every sequence of constellations \((p^k)_{k\in \mathbb {N}}\) such that \(\lim _{k\rightarrow \infty } p^k = p \in {\mathcal {P}}^N\), \(\lim _{k\rightarrow \infty } \varphi (v,p^k) = \varphi (v,p)\) for every \((N,v)\in {\mathcal {V}}^N\).
Compared to Theorem 3.1, in the following characterization of the Owen–Shapley spatial power index for fixed player set N, the dummy property is replaced by the weak dummy property and positional continuity.
Theorem 4.1
The Owen–Shapley spatial power index \(\Phi \) is the unique spatial power index on the class of spatial games with player set N satisfying EPC, WDP, PC, AN, RI, and PI.
In order to prove this theorem we first consider unanimity games. Until further notice the spatial power index \(\varphi \) is assumed to satisfy the six axioms in the theorem.
Lemma 4.2
Let \(i \in N\). Then \(\varphi _i(u_{\{i\}},p)=1\) and \(\varphi _j(u_{\{i\}},p)=0\) for all \(j\in N\setminus \{i\}\) and all \(p\in {\mathcal {P}}^N\).
Proof
Straightforward from the definition of a power index and WDP. \(\square \)
Recall that in a unanimity spatial game \((u_T,p)\), \(T_p \subseteq T\) denotes the set of non-dummies.
Lemma 4.3
Let \(T \subseteq N\) with \(|T| \ge 2\), let \(i,j\in T\) with \(i \ne j\), and suppose that \(T_p=\{i,j\}\). Then \(\varphi _i(u_T,p) = \varphi _j(u_T,p) = \frac{1}{2}\) and \(\varphi _k(u_T,p)=0\) for all \(k \in N \setminus \{i,j\}\).
Proof
By WDP and the definition of a power index we have \(\varphi _k(u_T,p)=0\) for all \(k \in N \setminus \{i,j\}\), \(\varphi _i(u_T,p),\ \varphi _i(u_T,p) \ge 0\), and \(\varphi _i(u_T,p) + \varphi _i(u_T,p) = 1\). For each \(k \in T \setminus \{i,j\}\) we have \(p_k \in \, ]p_i,p_j[\) and for each \(k \in N \setminus T\) with \(p_k \in (\leftarrow , p_i, p_j, \rightarrow )\) we may assume by PI that \(p_k \in \, ]p_i,p_j[\). Moreover, we may assume, again by PI, that all these points are symmetrically located with respect to \(\frac{1}{2} p_i + \frac{1}{2} p_j\), e.g., dividing the line segment \([p_i,p_j]\) in pieces of equal length. For each \(k \in N \setminus T\) with \(p_k \notin (\leftarrow , p_i, p_j, \rightarrow )\), note that by shifting in the direction of \(p_i\) or \(p_j\), possibly in both directions consecutively, we may shift \(p_k\) to any point y with \(||y-p_i|| = ||y - p_j||\) on the same side of \((\leftarrow , p_i, p_j, \rightarrow )\) as \(p_k\). In particular therefore, we may assume that any point \(p_k\) with \(k \in N \setminus T\) with \(p_k \notin (\leftarrow , p_i, p_j, \rightarrow )\) has \(||p_k-p_i|| = ||p_k - p_j||\). Then, by AN and RI, we obtain \(\varphi _i(u_T,p) = \varphi _j(u_T,p) = \frac{1}{2}\). \(\square \)
In the preceding lemma PC was not used. In the next lemma we show that the power of a non-dummy in a spatial unanimity game depends only on the angle at the position of this player in the constellation. The proof of this lemma uses PC – see also Remark 4.8.
Lemma 4.4
Let \((u_T,p)\) and \((u_S,q)\) be spatial games such that \(|T_p|,\ |S_q| \ge 3\). Let \(p_f\) be adjacent to \(p_g\) and \(p_g\) adjacent to \(p_h\) in \({ \text{ co } }\{p_d \mid d \in T_p\}\), and let \(q_i\) be adjacent to \(q_j\) and \(q_j\) adjacent to \(q_k\) in \({ \text{ co } }\{q_d \mid d \in S_q\}\). Suppose that \(\measuredangle \,p_f p_g p_h = \measuredangle \,q_i q_j q_k\). Then \(\varphi _g(u_T,p) = \varphi _j(u_S,q)\).
Proof
The proof proceeds in two steps.
(a) Consider a spatial game \((u_T,\hat{p})\) such that \(\hat{p}_g = p_g\), \(\hat{p}_f \in [p_g,p_f,\rightarrow )\) with \(||\hat{p}_f-p_g||=1\), \(\hat{p}_h \in [p_g,p_h,\rightarrow )\) with \(||\hat{p}_h-p_g||=1\), and \(\hat{p}_d \in { \text{ co } }\{\hat{p}_f, \hat{p}_g, \hat{p}_h\}\) for all \(d \in N \setminus \{f,g,h\}\) such that \(\{ \hat{p}_d \mid d \in N\} = \{ \hat{p}^\ell _d \mid d \in N\}\), where \(\ell \) is the straight line through \(\hat{p}_g\) and \(\frac{1}{2} \hat{p}_f + \frac{1}{2} \hat{p}_h\). We claim that \(\varphi _g(u_T,p)=\varphi _g(u_T,\hat{p})\).
To prove this, first observe that by PI, we have \(\varphi _g(u_T,p)=\varphi _g(u_T,p')\) for any \(p'\in {\mathcal {P}}^N\) such that \(p'_g = p_g = \hat{p}_g\), \(p'_f = \hat{p}_f\), \(p'_h = \hat{p}_h\), and \(p'_d \in [p_g, p_d, \rightarrow )\) for all \(d \in N \setminus \{f,g,h\}\). Also by PI, \(\varphi _g(u_T,\hat{p})=\varphi _g(u_T,p'')\) for any \(p''\in {\mathcal {P}}^N\) such that \(p''_g = p_g = \hat{p}_g\), \(p''_f = \hat{p}_f\), \(p''_h = \hat{p}_h\), and \(p''_d \in [p_g, \hat{p}_d, \rightarrow )\) for all \(d \in N \setminus \{f,g,h\}\). Since we may choose the points \(p'_d\) and \(p''_d\) as close to \(p_g\) as desired, we conclude by PC that \(\varphi _g(u_T,p)=\varphi _g(u_T,\hat{p})\).
(b) Similarly as in (a) we can find a constellation \(\hat{q}\) such that \(\varphi _j(u_S,q)=\varphi _j(u_S,\hat{q})\) and such that \(\hat{q}\) can be obtained from \(\hat{p}\) by appropriate reflections. By AN and RI we obtain \(\varphi _g(u_T,\hat{p}) = \varphi _j(u_S,\hat{q})\), and therefore \(\varphi _g(u_T,p) = \varphi _j(u_S,q)\). \(\square \)
In view of Lemma 4.4, similarly to what we did before, we introduce the notation \(\varphi (\alpha )\) to indicate the power of a non-dummy i in any spatial game \((u_T,p)\) with \(|T_p| \ge 3\), if the angle at \(p_i\) in the polytope \({ \text{ co } }\{p_d \mid d \in T_p\}\) is \(\alpha \in (0,\pi )\). Then we have:
Lemma 4.5
\(\varphi (\pi /2)=\frac{1}{4}\).
Proof
Let \(x := \varphi (\pi /2) \in [0,1]\). We claim that, for every \(k \in \mathbb {N}\),
The proof is by induction on k. For \(k=1\), we have \(\varphi (\pi /4)= (1-x)/2 = \frac{1}{2} - \frac{1}{2}x\), as desired, by considering (without loss of generality in view of Lemma 4.4) a triangle with one angle equal to \(\pi /2\) and the other angles equal to \(\pi /4\), and applying RI and AN. Now assume that (7) holds for \(k-1\). Then, by considering a triangle with one angle equal to \(\frac{1}{2^{k}}\pi \) and the other angles equal to \((\pi - \frac{1}{2^{k}}\pi )/2\), we obtain
by induction, which after simplification implies
Next, by considering a triangle with one angle equal to \(\pi /2\) and another angle equal to \(\frac{2^k-1}{2^{k+1}}\pi \), we obtain for the third angle
which concludes the proof of (7).
Now consider a sequence of triangles with vertices a, b, c(k), \(k\in \mathbb {N}\), such that the angles at a and b are equal to \(\frac{1}{2^{k+1}}\pi \). By PC, Lemma 4.3, and (7), we have
hence \(1-2x=\frac{1}{2}\), so that \(\varphi (\pi /2) = x = \frac{1}{4}\). \(\square \)
We proceed by observing that Lemmas 3.9 and 3.10 still apply; together with Lemma 4.5 we obtain:
Lemma 4.6
For all \(h,m \in \mathbb {N}\) such that \(m < 2^h\),
Since the function \(\varphi (\cdot )\) is continuous in view of PC, the following corollary follows from Lemma 4.6.
Corollary 4.7
For all \(\alpha \in (0,\pi )\),
Proof of Theorem 4.1
The Owen–Shapley spatial power index \(\Phi \) satisfies PC, and it satisfies all the other axioms by Theorem 3.1. A power index satisfying EPC is uniquely determined by its value on spatial games based on unanimity games. Uniqueness now follows from Lemmas 4.2 and 4.3, and Corollary 4.7. \(\square \)
Remark 4.8
The axioms in Theorem 4.1 are logically independent. For EPC, WDP, AN, RI, and PI, the power indexes \(\varphi ^1\) up to \(\varphi ^5\) in Sect. 3.3, respectively, are still valid examples. To show logical independence of PC, we adapt the power index \(\psi \) in Remark 3.15 as follows. Fix N with \(|N|\ge 3\). For a spatial game \((N,u_T,p)\) with with \(|T|=3\), let \(\psi _i(N,u_T,p)=1/|T_p|\) if \(i \in T_p\) and \(\psi _i(N,u_T,p)=0\) otherwise. For any other spatial game (N, v, p) let \(\psi (N,v,p)=\Phi (N,v,p)\).
5 Concluding remarks
The main result in this paper is a characterization of the Owen–Shapley spatial power index by means of five axioms. A limitation of our approach is that it is restricted to constellations and issues in \({\mathbb {R}}^2\). It is straightforward to extend the axioms to the case of constellations and issues in \({\mathbb {R}}^m\) for \(m>2\), and it is safe to conjecture that the Owen–Shapley spatial power index satisfies these extended axioms. A proof of an eventual converse, however, seems to be more involved, and it is not even clear whether such a converse would hold.
As far as we are aware, this is a first axiomatic characterization of a spatial power index. Further research may concern characterizations of alternative power indexes, as proposed in the literature.
Notes
Thus, in this paper simple games are monotonic by definition.
Also note that, even if (N, v) is proper—the complement of each winning coalition is losing—the game \((N\setminus \{i\},v_{-i})\) does not have to be proper.
Alternatively, one could include requirements such as Individual Rationality and Efficiency to obtain these conditions. As will be argued later in the paper, in particular in Remark 3.14, the nonnegativity condition is not innocent. The efficiency condition, however, is basically a normalization.
Verification of this claim follows from elementary geometry.
If \(k=2\) then \(\ell \) and m as well as \(\ell ^\bot \) and \(m^\bot \) coincide.
The existence of such a function g can be shown using the Axiom of Choice.
References
Alonso-Meijide JM, Fiestras-Janeiro MG, García-Jurado I (2011) A new power index for spatial games. In: Modern Mathematical tools and techniques in capturing complexity understanding complex systems, pp 275–285
Benati S, Marzetti GV (2013) Probabilistic spatial power indexes. Soc Choice Welf 40:391–410
Bertini C, Freixas J, Gambarelli G, Stach I (2013) Comparing power indices. Int Game Theory Rev 2:1340004-1–1340004-19
Blockmans T, Guerry MA (2015) Probabilistic spatial power indexes: the impact of issue saliences and and distance selection. Group Decis Negot 24:675–697
Braham M, Holler M (2005) The impossibility of a preference-based power index. J Theor Polit 17:137–157
Derks J, Haller H (1999) Null players out? Linear values for games with variable support. Int Game Theory Rev 1:301–314
Dubey P (1975) On the uniqueness of the Shapley value. Int J Game Theory 4:131–139
Dubey P, Einy E, Haimanko O (2005) Compound voting and the Banzhaf index. Games Econ Behav 51:20–30
Einy E (1987) Semivalues of simple games. Math Oper Res 12:185–192
Einy E, Haimanko O (2011) Characterization of the Shapley–Shubik power index without the efficiency axiom. Games Econ Behav 73:615–621
Enelow J, Hinich M (1984) The spatial theory of voting: an introduction. Cambridge University Press, Cambridge
Enelow J, Hinich M (eds) (1990) Advances in the spatial theory of voting. Cambridge University Press, Cambridge
Grofman B, Owen G, Noviello N, Glazer A (1987) Stability and centrality of legislative choice in the spatial context. Am Polit Sci Rev 81:539–553
Martin M, Nganmeni Z, Tchantcho B (2014) The Owen and Shapley spatial power indices: a comparison and a generalization. Working paper, THEMA, Cergy Pontoise
Napel S, Widgrén M (2005) The possibility of a preference-based power index. J Theor Polit 17:377–387
Owen G (1971) Political games. Nav Res Logist Quart 18:345–354
Owen G, Shapley LS (1989) Optimal location of candidates in ideological space. Int J Game Theory 18:339–356
Passarelli F, Bar J (2007) Preferences, the agenda setter, and the distribution of power in the EU. Soc Choice Welf 28:41–60
Shapley LS (1977) A comparison of power indices and a non-symmetric generalization. Paper P5872, Rand Corporation, Santa Monica, CA
Shenoy PP (1982) The Banzhaf power index for political games. Math Soc Sci 2:299–315
Straffin PD Jr (1994) Power and stability in politics, Chapter 32. In: Aumann RJ, Hart S (eds) Handbook of game theory and economics applications. Elsevier, Amsterdam
Author information
Authors and Affiliations
Corresponding author
Additional information
This research has been partially supported by the Ministerio de Economia y Competitividad (ECO2015-66803-P), and The University of the Basque Country (GIU13/31, UFI11/51). We thank two anonymous reviewers for their constructive comments.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Peters, H., Zarzuelo, J.M. An axiomatic characterization of the Owen–Shapley spatial power index. Int J Game Theory 46, 525–545 (2017). https://doi.org/10.1007/s00182-016-0544-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-016-0544-8