Near-field (mathematics)

In mathematics, a near-field is an algebraic structure similar to a division ring, except that it has only one of the two distributive laws. Alternatively, a near-field is a near-ring in which there is a multiplicative identity and every non-zero element has a multiplicative inverse.

Contents

• Definition
• Notes on the definition
• Examples
• History and applications
• Description in terms of Frobenius groups and group automorphisms
• Classification
• See also
• References
• External links

Definition

A near-field is a set ${\displaystyle Q}$ together with two binary operations, ${\displaystyle +}$ (addition) and ${\displaystyle \cdot }$ (multiplication), satisfying the following axioms:

A1: ${\displaystyle (Q,+)}$ is an abelian group.

A2: ${\displaystyle (a\cdot b)\cdot c}$ = ${\displaystyle a\cdot (b\cdot c)}$ for all elements ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ of ${\displaystyle Q}$ (The associative law for multiplication).

A3: ${\displaystyle (a+b)\cdot c=a\cdot c+b\cdot c}$ for all elements ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ of ${\displaystyle Q}$ (The right distributive law).

A4: ${\displaystyle Q}$ contains a non-zero element 1 such that ${\displaystyle 1\cdot a=a\cdot 1=a}$ for every element ${\displaystyle a}$ of ${\displaystyle Q}$ (Multiplicative identity).

A5: For every non-zero element ${\displaystyle a}$ of ${\displaystyle Q}$ there exists an element ${\displaystyle a^{-1}}$ such that ${\displaystyle a\cdot a^{-1}=1=a^{-1}\cdot a}$ (Multiplicative inverse).

Examples

1. Any division ring (including any field) is a near-field.
2. The following defines a (right) near-field of order 9. It is the smallest near-field which is not a field.

   Let ${\displaystyle K}$ be the Galois field of order 9. Denote multiplication in ${\displaystyle K}$ by ' ${\displaystyle *}$ '. Define a new binary operation ' · ' by:

   If ${\displaystyle b}$ is any element of ${\displaystyle K}$ which is a square and ${\displaystyle a}$ is any element of ${\displaystyle K}$ then ${\displaystyle a\cdot b=a*b}$.

   If ${\displaystyle b}$ is any element of ${\displaystyle K}$ which is not a square and ${\displaystyle a}$ is any element of ${\displaystyle K}$ then ${\displaystyle a\cdot b=a^{3}*b}$.

   Then ${\displaystyle K}$ is a near-field with this new multiplication and the same addition as before. ^[4]

History and applications

The concept of a near-field was first introduced by Leonard Dickson in 1905. He took division rings and modified their multiplication, while leaving addition as it was, and thus produced the first known examples of near-fields that were not division rings. The near-fields produced by this method are known as Dickson near-fields; the near-field of order 9 given above is a Dickson near-field. Hans Zassenhaus proved that all but 7 finite near-fields are either fields or Dickson near-fields. ^[2]

The earliest application of the concept of near-field was in the study of incidence geometries such as projective geometries. ^{[5] [6]} Many projective geometries can be defined in terms of a coordinate system over a division ring, but others can not. It was found that by allowing coordinates from any near-ring the range of geometries which could be coordinatized was extended. For example, Marshall Hall used the near-field of order 9 given above to produce a Hall plane, the first of a sequence of such planes based on Dickson near-fields of order the square of a prime. In 1971 T. G. Room and P.B. Kirkpatrick provided an alternative development. ^[7]

There are numerous other applications, mostly to geometry. ^[8] A more recent application of near-fields is in the construction of ciphers for data-encryption, such as Hill ciphers. ^[9]

Description in terms of Frobenius groups and group automorphisms

Let ${\displaystyle K}$ be a near field. Let ${\displaystyle K_{m}}$ be its multiplicative group and let ${\displaystyle K_{a}}$ be its additive group. Let ${\displaystyle c\in K_{m}}$ act on ${\displaystyle b\in K_{a}}$ by ${\displaystyle b\mapsto b\cdot c}$. The axioms of a near field show that this is a right group action by group automorphisms of ${\displaystyle K_{a}}$, and the nonzero elements of ${\displaystyle K_{a}}$ form a single orbit with trivial stabilizer.

Conversely, if ${\displaystyle A}$ is an abelian group and ${\displaystyle M}$ is a subgroup of ${\displaystyle \mathrm {Aut} (A)}$ which acts freely and transitively on the nonzero elements of ${\displaystyle A}$, then we can define a near field with additive group ${\displaystyle A}$ and multiplicative group ${\displaystyle M}$. Choose an element in ${\displaystyle A}$ to call ${\displaystyle 1}$ and let ${\displaystyle \phi :M\to A\setminus \{0\}}$ be the bijection ${\displaystyle m\mapsto 1\ast m}$. Then we define addition on ${\displaystyle A}$ by the additive group structure on ${\displaystyle A}$ and define multiplication by ${\displaystyle a\cdot b=1\ast \phi ^{-1}(a)\phi ^{-1}(b)}$.

A Frobenius group can be defined as a finite group of the form ${\displaystyle A\rtimes M}$ where ${\displaystyle M}$ acts without stabilizer on the nonzero elements of ${\displaystyle A}$. Thus, near fields are in bijection with Frobenius groups where ${\displaystyle |M|=|A|-1}$.

Classification

As mentioned above, Zassenhaus proved that all finite near fields either arise from a construction of Dickson or are one of seven exceptional examples. We will describe this classification by giving pairs ${\displaystyle (A,M)}$ where ${\displaystyle A}$ is an abelian group and ${\displaystyle M}$ is a group of automorphisms of ${\displaystyle A}$ which acts freely and transitively on the nonzero elements of ${\displaystyle A}$.

The construction of Dickson proceeds as follows. ^[10] Let ${\displaystyle q}$ be a prime power and choose a positive integer ${\displaystyle n}$ such that all prime factors of ${\displaystyle n}$ divide ${\displaystyle q-1}$ and, if ${\displaystyle q\equiv 3{\bmod {4}}}$, then ${\displaystyle n}$ is not divisible by ${\displaystyle 4}$. Let ${\displaystyle F}$ be the finite field of order ${\displaystyle q^{n}}$ and let ${\displaystyle A}$ be the additive group of ${\displaystyle F}$. The multiplicative group of ${\displaystyle F}$, together with the Frobenius automorphism ${\displaystyle x\mapsto x^{q}}$ generate a group of automorphisms of ${\displaystyle F}$ of the form ${\displaystyle C_{n}\ltimes C_{q^{n}-1}}$, where ${\displaystyle C_{k}}$ is the cyclic group of order ${\displaystyle k}$. The divisibility conditions on ${\displaystyle n}$ allow us to find a subgroup of ${\displaystyle C_{n}\ltimes C_{q^{n}-1}}$ of order ${\displaystyle q^{n}-1}$ which acts freely and transitively on ${\displaystyle A}$. The case ${\displaystyle n=1}$ is the case of commutative finite fields; the nine element example above is ${\displaystyle q=3}$, ${\displaystyle n=2}$.

In the seven exceptional examples, ${\displaystyle A}$ is of the form ${\displaystyle C_{p}^{2}}$. This table, including the numbering by Roman numerals, is taken from Zassenhaus's paper. ^[2]

	${\displaystyle A=C_{p}^{2}}$	Generators for ${\displaystyle M}$	Description(s) of ${\displaystyle M}$
I	${\displaystyle p=5}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}1&-2\\-1&-2\\\end{smallmatrix}}\right)}$	${\displaystyle 2T}$, the binary tetrahedral group.
II	${\displaystyle p=11}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}1&5\\-5&-2\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}4&0\\0&4\\\end{smallmatrix}}\right)}$	${\displaystyle 2T\times C_{5}}$
III	${\displaystyle p=7}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}1&3\\-1&-2\\\end{smallmatrix}}\right)}$	${\displaystyle 2O}$, the binary octahedral group.
IV	${\displaystyle p=23}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}1&-6\\12&-2\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}2&0\\0&2\\\end{smallmatrix}}\right)}$	${\displaystyle 2O\times C_{11}}$
V	${\displaystyle p=11}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}2&4\\1&-3\\\end{smallmatrix}}\right)}$	${\displaystyle 2I}$, the binary icosahedral group.
VI	${\displaystyle p=29}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}1&-7\\-12&-2\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}16&0\\0&16\\\end{smallmatrix}}\right)}$	${\displaystyle 2I\times C_{7}}$
VII	${\displaystyle p=59}$	${\displaystyle \left({\begin{smallmatrix}0&-1\\1&0\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}9&15\\-10&-10\\\end{smallmatrix}}\right)}$${\displaystyle \left({\begin{smallmatrix}4&0\\0&4\\\end{smallmatrix}}\right)}$	${\displaystyle 2I\times C_{29}}$

The binary tetrahedral, octahedral and icosahedral groups are central extensions of the rotational symmetry groups of the platonic solids; these rotational symmetry groups are ${\displaystyle A_{4}}$, ${\displaystyle S_{4}}$ and ${\displaystyle A_{5}}$ respectively. ${\displaystyle 2T}$ and ${\displaystyle 2I}$ can also be described as ${\displaystyle SL(2,\mathbb {F} _{3})}$ and ${\displaystyle SL(2,\mathbb {F} _{5})}$.

See also

• Near-ring
• Planar ternary ring
• Quasifield

Related Research Articles

In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel.

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.

In mathematics, a finite field or Galois field is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subtraction and division are defined and satisfy certain basic rules. The most common examples of finite fields are given by the integers mod p when p is a prime number.

In mathematics, a group is a set with an operation that satisfies the following constraints: the operation is associative, has an identity element, and every element of the set has an inverse element.

In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototypical example of an abelian category is the category of abelian groups, Ab. The theory originated in an effort to unify several cohomology theories by Alexander Grothendieck and independently in the slightly earlier work of David Buchsbaum. Abelian categories are very stable categories; for example they are regular and they satisfy the snake lemma. The class of abelian categories is closed under several categorical constructions, for example, the category of chain complexes of an abelian category, or the category of functors from a small category to an abelian category are abelian as well. These stability properties make them inevitable in homological algebra and beyond; the theory has major applications in algebraic geometry, cohomology and pure category theory.

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.

In mathematics, the endomorphisms of an abelian group X form a ring. This ring is called the endomorphism ring of X, denoted by End(X); the set of all homomorphisms of X into itself. Addition of endomorphisms arises naturally in a pointwise manner and multiplication via endomorphism composition. Using these operations, the set of endomorphisms of an abelian group forms a (unital) ring, with the zero map as additive identity and the identity map as multiplicative identity.

In mathematics, an algebraic structure consists of a nonempty set A, a collection of operations on A, and a finite set of identities, known as axioms, that these operations must satisfy.

In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory.

In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free-modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.

In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a ring. The concept of module generalizes also the notion of abelian group, since the abelian groups are exactly the modules over the ring of integers.

In algebra, a valuation is a function on a field that provides a measure of the size or multiplicity of elements of the field. It generalizes to commutative algebra the notion of size inherent in consideration of the degree of a pole or multiplicity of a zero in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic or analytic varieties in algebraic geometry. A field with a valuation on it is called a valued field.

In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring, and its basis is the set of elements of the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.

In abstract algebra, a semiring is an algebraic structure. It is a generalization of a ring, dropping the requirement that each element must have an additive inverse. At the same time, it is a generalization of bounded distributive lattices.

In mathematics and group theory, the term multiplicative group refers to one of the following concepts:

In mathematics, the Grothendieck group, or group of differences, of a commutative monoid M is a certain abelian group. This abelian group is constructed from M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.

Abstract analytic number theory is a branch of mathematics which takes the ideas and techniques of classical analytic number theory and applies them to a variety of different mathematical fields. The classical prime number theorem serves as a prototypical example, and the emphasis is on abstract asymptotic distribution results. The theory was invented and developed by mathematicians such as John Knopfmacher and Arne Beurling in the twentieth century.

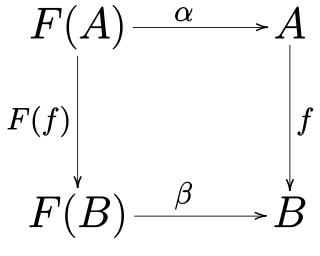
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

In mathematics, a quasifield is an algebraic structure where and are binary operations on , much like a division ring, but with some weaker conditions. All division rings, and thus all fields, are quasifields.

References

External links

• Nearfields by Hauke Klein.