In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium.

In thermodynamics, the specific heat capacity of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat capacity or as the specific heat. More formally it is the heat capacity of a sample of the substance divided by the mass of the sample. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−1⋅K−1.

Stoichiometry is the relationship between the weights of reactants and products before, during, and following chemical reactions.

In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
Solubility equilibrium is a type of dynamic equilibrium that exists when a chemical compound in the solid state is in chemical equilibrium with a solution of that compound. The solid may dissolve unchanged, with dissociation, or with chemical reaction with another constituent of the solution, such as acid or alkali. Each solubility equilibrium is characterized by a temperature-dependent solubility product which functions like an equilibrium constant. Solubility equilibria are important in pharmaceutical, environmental and many other scenarios.
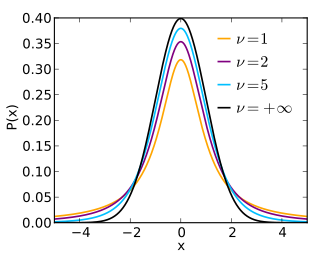
In probability and statistics, Student's t distribution is a continuous probability distribution that generalizes the standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped.
A chemical equation is the symbolic representation of a chemical reaction in the form of symbols and chemical formulas. The reactant entities are given on the left-hand side and the product entities are on the right-hand side with a plus sign between the entities in both the reactants and the products, and an arrow that points towards the products to show the direction of the reaction. The chemical formulas may be symbolic, structural, or intermixed. The coefficients next to the symbols and formulas of entities are the absolute values of the stoichiometric numbers. The first chemical equation was diagrammed by Jean Beguin in 1615.
The standard enthalpy of reaction for a chemical reaction is the difference between total product and total reactant molar enthalpies, calculated for substances in their standard states. The value can be approximately interpreted in terms of the total of the chemical bond energies for bonds broken and bonds formed.

The unified neutral theory of biodiversity and biogeography is a theory and the title of a monograph by ecologist Stephen P. Hubbell. It aims to explain the diversity and relative abundance of species in ecological communities. Like other neutral theories of ecology, Hubbell assumes that the differences between members of an ecological community of trophically similar species are "neutral", or irrelevant to their success. This implies that niche differences do not influence abundance and the abundance of each species follows a random walk. The theory has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse.
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.
The principle of detailed balance can be used in kinetic systems which are decomposed into elementary processes. It states that at equilibrium, each elementary process is in equilibrium with its reverse process.
The molar conductivity of an electrolyte solution is defined as its conductivity divided by its molar concentration.
Equilibrium constants are determined in order to quantify chemical equilibria. When an equilibrium constant K is expressed as a concentration quotient,
An osmotic coefficient is a quantity which characterises the deviation of a solvent from ideal behaviour, referenced to Raoult's law. It can be also applied to solutes. Its definition depends on the ways of expressing chemical composition of mixtures.
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. They were first described by physical chemist Kenneth Pitzer. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise interactions amongst ions and solvent. The derivation is thermodynamically rigorous at a given level of expansion. The parameters may be derived from various experimental data such as the osmotic coefficient, mixed ion activity coefficients, and salt solubility. They can be used to calculate mixed ion activity coefficients and water activities in solutions of high ionic strength for which the Debye–Hückel theory is no longer adequate. They are more rigorous than the equations of specific ion interaction theory, but Pitzer parameters are more difficult to determine experimentally than SIT parameters.
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.
In chemistry, ion transport number, also called the transference number, is the fraction of the total electric current carried in an electrolyte by a given ionic species i:
Geochemical modeling or theoretical geochemistry is the practice of using chemical thermodynamics, chemical kinetics, or both, to analyze the chemical reactions that affect geologic systems, commonly with the aid of a computer. It is used in high-temperature geochemistry to simulate reactions occurring deep in the Earth's interior, in magma, for instance, or to model low-temperature reactions in aqueous solutions near the Earth's surface, the subject of this article.

Total inorganic carbon is the sum of the inorganic carbon species.














