Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Nov 1.
Published in final edited form as: Proc SPIE Int Soc Opt Eng. 2022 Apr 4;12032:1203215. doi: 10.1117/12.2613146

Cranial Meninges Reconstruction Based on Convolutional Networks and Deformable Models: Applications to Longitudinal Study of Normal Aging

Peiyu Duan a,*, Shuo Han a,*, Lianrui Zuo b,c, Yang An c, Yihao Liu b, Ahmed Alshareef b, Junghoon Lee d, Aaron Carass b, Susan M Resnick c, Jerry L Prince a,b
PMCID: PMC9623767  NIHMSID: NIHMS1845145  PMID: 36325254

Abstract

The cranial meninges are membranes enveloping the brain. The space between these membranes contains mainly cerebrospinal fluid. It is of interest to study how the volumes of this space change with respect to normal aging. In this work, we propose to combine convolutional neural networks (CNNs) with nested topology-preserving geometric deformable models (NTGDMs) to reconstruct meningeal surfaces from magnetic resonance (MR) images. We first use CNNs to predict implicit representations of these surfaces then refine them with NTGDMs to achieve sub-voxel accuracy while maintaining spherical topology and the correct anatomical ordering. MR contrast harmonization is used to match the contrasts between training and testing images. We applied our algorithm to a subset of healthy subjects from the Baltimore Longitudinal Study of Aging for demonstration purposes and conducted longitudinal statistical analysis of the intracranial volume (ICV) and subarachnoid space (SAS) volume. We found a statistically significant decrease in the ICV and an increase in the SAS volume with respect to normal aging.

Keywords: Meninges, longitudinal study, convolutional networks, deformable models, MRI, harmonization

1. INTRODUCTION

The cranial meninges are thin membranes enclosing the brain. They comprise three layers: dura mater, arachnoid mater, and pia mater. The three layers of meninges help maintain the mechanics, homeostasis, and immune response of the central nervous system.1 The dura mater is directly adherent to the inner surface of the skull, and there is typically no space between the dura and arachnoid. The subarachnoid space (SAS)—the space between the arachnoid and pia—mainly contains the cerebrospinal fluid (CSF). CSF serves as a nutrient delivery and waste removal system for the brain,2 and it is manufactured continuously in brain ventricles. Because of the importance of CSF, we are interested in analyzing the size change of the SAS space to study how the CSF is distributed during normal aging, and it can also provide an alternative way to study brain atrophy. We are also interested in studying the size of the intracranial volume (ICV)—i.e., the total volume of the cranial cavity3 enclosed by the dura mater—during normal aging since ICV has often been used to adjust for the head size when studying the sizes of brain structures.3, 4 Despite the importance of the SAS and ICV, very limited study has been done for automatically segmenting the meninges and observing their longitudinal changes.

The ultra-thinness of meningeal layers (0.015–0.04 mm for the arachnoid5 and the pia,6 and an average of 0.36 mm for the dura7) makes it difficult to directly segment them from conventional magnetic resonance (MR) images. Therefore, we chose to use implicit representations—i.e., occupancy and signed distance functions—to reconstruct the surfaces of the meninges. An occupancy function is equivalent to a soft segmentation of the voxels inside a surface. A signed distance function represents the distance between a surface and all image voxels, and the distances of the voxels that are inside this surface have a negative sign. We built our meningeal surface reconstruction upon a previous algorithm.8 That work uses a nested topology-preserving geometric deformable model (NTGDM)9 with the region force calculated from a multi-atlas segmentation to deform the signed distance function of only the arachnoid. In comparison, our work uses two NTGDMs with the region forces calculated from deep convolutional neural networks (CNNs) for both the dura and the arachnoid. Specifically, we first use two 2D U-Nets10 to estimate the occupancy of the dura and arachnoid surfaces from coregistered T1-weighted (T1w) and T2-weighted (T2w) MR images; we then convert these occupancy maps into region forces and initial signed distance functions to refine them with NTGDMs. NTGDMs can guarantee the meningeal surfaces to have a spherical topology and a correct anatomical ordering (i.e., the arachnoid surface should be inside the dura surface, and the pia surface should inside the arachnoid surface). NTGDMs also output explicit surfaces as triangular meshes that have sub-voxel accuracy (i.e., not limited by the voxel size of a digital image). The pia surface is estimated by another algorithm called SLANT-CRUISE.11, 12

We applied our algorithm to 56 healthy participants with 243 MR imaging sessions from the Baltimore Longitudinal Study of Aging (BLSA).13 The manual delineations from Singh et al.14 and Roy et al.15 were used to train our networks. Since MR images from different sites potentially do not have similar contrasts even for the same modality, we also harmonized these training images (both T1w and T2w) to the BLSA contrasts using CALAMITI.16, 17 We further manually corrected three predictions from each network to fine-tune them for more robust results. In our longitudinal analyses, we used the volume enclosed by our estimated epidural surface as the ICV. The SAS volume is calculated as the volume between our estimated arachnoid surface and the pia surface from SLANT-CRUISE. Linear mixed effect models18 were used to study the longitudinal changes of the ICV and the SAS volume.

2. METHODS

2.1. Data

We selected 56 subjects from the BLSA, comprising 28 age-matched cognitively normal males and females, with 243 visits in total. We use the age at the first visit as the baseline age and define the follow-up interval as the age difference in years between a visit and the baseline age. The baseline ages for all subjects range from 70 to 88 years with an average of 78.24 years for the females and 78.15 years for the males. The follow-up intervals range from 0.8–10.7 years (average 2.97 years) for all subjects. For our processing, we used paired T1w and T2w MR images.

2.2. Reconstruction of Meningeal Surfaces

The T1w and T2w images were inhomogeneity-corrected using N4.19 The mean white matter intensity of each contrast was separately normalized to 1,000.20 The T2w images were further super-resolved in the through-plane direction using SMORE.21, 22 The T1w, T2w, and corresponding manual delineations were coregistered into 0.8×0.8×0.8 mm3 MNI space.23 The training data,14, 15 containing 6 and 20 subjects for the arachnoid and dura surfaces, respectively, were harmonized to the BLSA contrasts using CALAMITI.16, 17 We used SLANT-CRUISE11, 12 to reconstruct the pia surface.

We trained two 2D U-Nets10 independently, one for the dura and one for the arachnoid, to predict their occupancy maps. The network architecture is shown in Fig 1. Our modified U-Net contains 64 channels after the first convolution block and 5 downsampling steps. 2D slices of paired T1w and T2w images, which were extracted from all three of axial, coronal, and sagittal orientations, were used as a double-channel input to the networks. Both networks were optimized using the Adam optimizer24 with a learning rate of 2 × 10−4 for 100 epochs and a mini-batch size of 8. During testing, the network was applied to all 2D slices from all three orientations, and the three predicted 3D occupancy maps were combined using a voxel-wise median. Although we harmonized the training data into the BLSA contrasts, the predictions were still not robust. Therefore, we manually corrected three predicted occupancy masks for each of our two networks to fine-tune them for another 10 epochs. There was no further manual intervention after network fine-tuning.

Figure 1.

Figure 1.

Open in a new tab

The 2D U-Net CNN structure. In the downsampling path, we decrease the image height and width by a factor of 2, and increase the image channels by a factor of 2 each time. The maximum number of channels in the downsampling path is capped at 1,024. In the upsampling path, we increase the image height and width by a factor of 2 with upsampling and decrease the image channels by a factor of 2 each time. The result of each downsampling block is concatenated with the upsampling block result shown as green arrows. The output of the image contains 2 channels to output the occupancy maps of the dura and arachnoid surfaces.

After we obtained the occupancy maps, we applied two NTGDMs to reconstruct the arachnoid and dura surfaces. We rescaled the occupancy values to the range [−1, 1] as the region forces to be used in NTGDMs. We used the largest connected-component of the thresholded occupancy map (greater than 0.5) and a topology-correction algorithm25 to generate a signed distance function with a spherical topology (a single closed surface without holes or handles) as the initial levelset of each NTGDM. The inner levelsets for NTGDMs of the arachnoid and dura were set as the pia and arachnoid surfaces, respectively, to guarantee the anatomical ordering of these surfaces. The weights for the curvature and region forces were set to 0.2 and 2, respectively. Finally, we calculated the ICV as the volume enclosed by the dura surface and the SAS volume as the volume between the arachnoid and pia surfaces using the triangular meshes that were generated from our NTGDMs.

2.3. Statistical Analysis

We used two linear mixed effects models (LME) in R version 4.0.3 with the library nlme18 to study the longitudinal changes of ICVs and SAS volumes. The fixed effects for the ICVs were the intercept, follow-up interval, baseline age, and biological sex. The fixed effects for the SAS volumes were the intercept, follow-up interval, baseline age, sex, and ICV at the baseline visit. The baseline ages were centered around the mean of all subjects, i.e., 78.95 years. For the biological sex, we used 0.5 to indicate males and −0.5 to indicate females. The random effects were the intercept and follow-up interval for both models. We then tested whether the coefficients of the fixed effects were significantly different from 0 (p < 0.05).

3. RESULTS

Figure 2 shows example reconstructions of meningeal surfaces of two subjects overlaid on their corresponding T1w and T2w images. Each color represents the reconstruction of a different meningeal layer.

Figure 2.

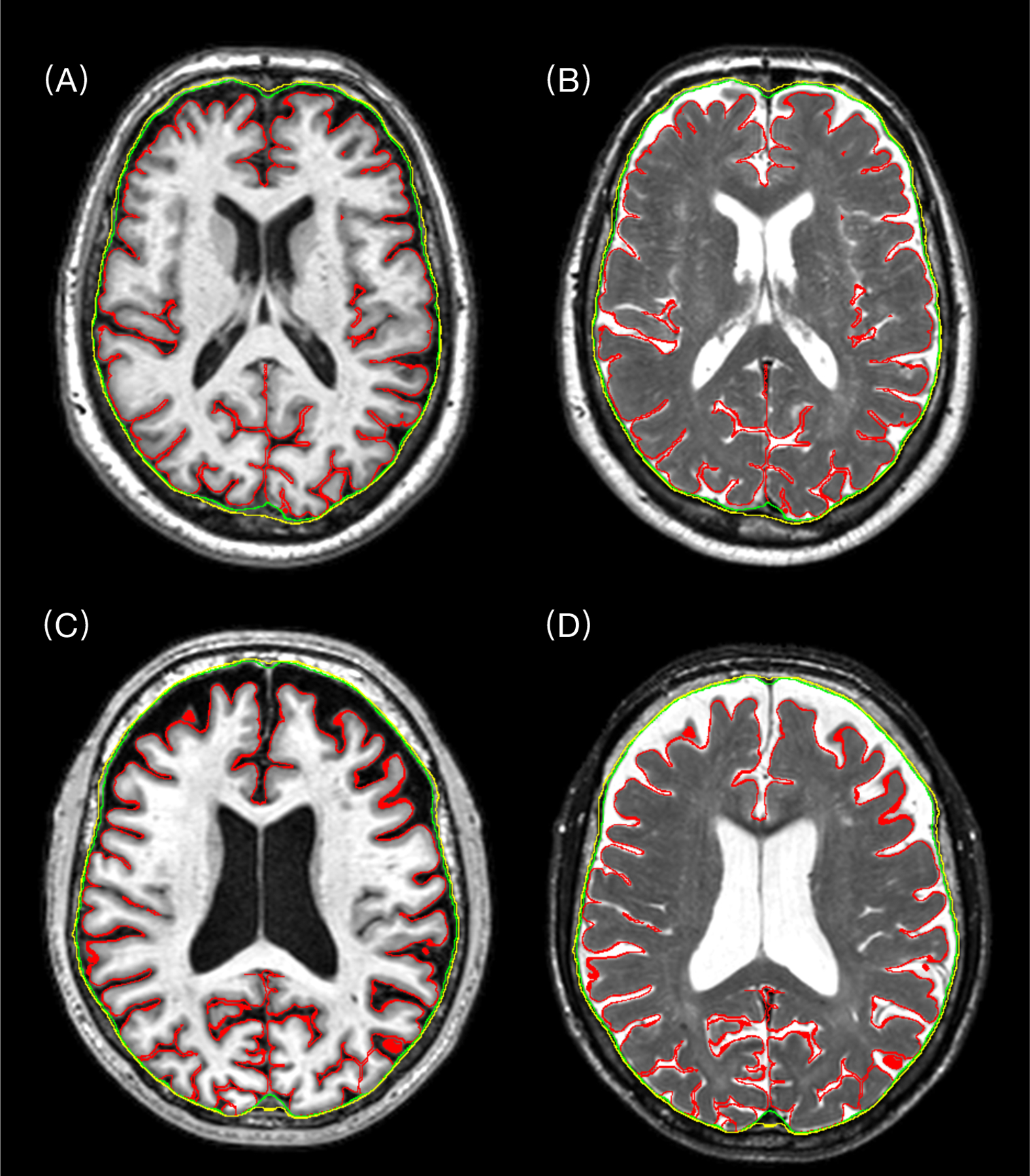
Figure 2.

Open in a new tab

Example reconstructions of dura (yellow), arachnoid (green), and pia (red) surfaces. (A) and (B) are T1w and T2w images of a subject, respectively. (C) and (D) are T1w and T2w images of another subject, respectively. The surfaces are interpolated into the voxel grids of the T1w and T2w image slices.

We removed 31 failed cases, resulting in 212 visits in total for the following LME analyses. The volumes from all visits of all subjects are plotted in Fig. 3. The LME results are shown in Table 1. Both the sex and follow-up interval are significant for the ICV. Males have statistically significant larger ICVs than females. Although the ICV is not significantly correlated with the baseline age cross-sectionally, it significantly decreases over time. For the SAS volume, it is not significantly correlated with the biological sex after adjusting for the ICV. Both the baseline age and follow-up interval are significant, which indicates that the SAS volume is larger at a higher baseline age and increases over time. We also plot the LME fits in Fig. 4.

Figure 3.

Figure 3.

Open in a new tab

The trajectories of individual volumes of all subjects and visits. Each dot represents the volume measurement at a visit from an individual. Males and females are plotted in blue and red, respectively. (A) is ICVs, and (B) is SAS volumes.

Table 1.

Fixed-effect coefficients (β), standard error (SE), and p-values (p) for the sex, baseline age, and follow-up interval. Statistically significant effects with p-values ≤ 0.05 are highlighted in bold.

ICV
 SAS volume
β SE p-value β SE p-value
Sex 144.60 28.91 6.87 × 10 −6 9.54 11.51 0.41
Baseline age −2.01 2.66 0.45 1.87 0.87 3.66 × 10 −2
Follow-up interval −1.38 0.23 1.35 × 10 −8 2.42 0.41 2.82 × 10 −8
Open in a new tab

Figure 4.

Figure 4.

Open in a new tab

The longitudinal trajectories of fixed effects for ICVs and SAS volumes. The trajectories are calculated by applying the fitted coefficients (β in Table 1) to the fixed effects. Each solid line segment is is plotted with the baseline age at its start year and with follow-up intervals covering 5 years. Males and females are plotted in blue and red, respectively. (A) is ICVs, and (B) is SAS volumes. In (B), we use the average ICV for both sexes 1526 mL in the fitted LME model to plot the volumes after adjusting for ICV.

4. DISCUSSION AND CONCLUSIONS

In this paper, we described a method to reconstruct the meningeal surfaces using CNNs and NTGDMs. The NTGDMs were performed as a post-processing step of the CNNs in our work. Our algorithm was applied to subjects from the BLSA to study longitudinal changes of ICVs and SAS volumes. We found that the coefficients of the baseline age and follow-up interval for the SAS volume were significantly different from 0, suggesting that the SAS volume is larger at a higher age and increases over time. It is surprising that the ICV decreases longitudinally based on our result even though ICVs are generally assumed to be constant after peaking in early adulthood.26 The decrease we observed in ICV analysis could be due to our limited sample size or algorithm bias, but we also note that a previous study using T1w brain scans found a ICV decrease starting from middle adulthood.27

Although for the SAS analysis, we have only reported volumes of SAS, it is also feasible to analyze the thicknesses of the SAS, both globally and locally, from our surface reconstructions. In the future, we plan to apply our algorithm to other cohorts to help us better understand brain atrophy during aging and disease. We are also investigating more advanced algorithms to incorporate the topology constraint and the anatomical ordering of the meninges into CNNs for future studies.

ACKNOWLEDGMENTS

The authors would like to thank BLSA participants and our colleagues. This research was supported in part by the Intramural Research Program of the NIH, National Institute on Aging and in part by the NIH through a NINDS grant R21 NS120286 (PI: J.L. Prince).

REFERENCES

  • [1].Walsh DR, Zhou Z, Li X, Kearns J, Newport DT, and Mulvihill JJ, “Mechanical properties of the cranial meninges: A systematic review,” Journal of Neurotrauma 38(13), 1748–1761 (2021). [DOI] [PubMed] [Google Scholar]
  • [2].Veening JG and Barendregt HP, “The regulation of brain states by neuroactive substances distributed via the cerebrospinal fluid; a review,” Cerebrospinal Fluid Research 7(1) (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [3].Voevodskaya O, Simmons A, Nordenskjöld R, Kullberg J, Ahlström, H., Lind, L., Wahlund, L., Larsson, E., Westman, E., and Alzheimer’s Disease Neuroimaging Initiative, “The effects of intracranial volume adjustment approaches on multiple regional MRI volumes in healthy aging and Alzheimer’s disease,” Frontiers in Aging Neuroscience 6, 264 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [4].Han S, An Y, Carass A, Prince JL, and Resnick SM, “Longitudinal analysis of regional cerebellum volumes during normal aging,” NeuroImage 220, 117062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [5].Reina MA, Prats-Galino A, Sola R, Puigdellívol-Sánchez A, Arriazu Navarro R, and De J, “structure of the arachnoid layer of the human spinal meninges: A barrier that regulates dural sac permeability” [DOI] [PubMed] [Google Scholar]
  • [6].Reina MA, Casasola OD, Villanueva MC, López A, Machés F, and De Andrés JA, “Ultrastructural findings in human spinal pia mater in relation to subarachnoid anesthesia,” Anesthesia amp; Analgesia, 1479–1485 (2004). [DOI] [PubMed] [Google Scholar]
  • [7].Fam M, Potash A, Potash M, Robinson R, Karnell L, O’Brien E, and Greenlee J, “Skull base dural thickness and relationship to demographic features: A postmortem study and literature review,” Journal of Neurological Surgery Part B: Skull Base 79(06), 614–620 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [8].Glaister J, Shao M, Li X, Carass A, Roy S, Blitz AM, Prince JL, and Ellingsen LM, “Deformable model reconstruction of the subarachnoid space,” in [Medical Imaging 2018: Image Processing ], 10574, 793–799, SPIE; (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [9].Han X, Pham DL, Tosun D, Rettmann ME, Xu C, and Prince JL, “CRUISE: Cortical reconstruction using implicit surface evolution,” NeuroImage 23(3), 997–1012 (2004). [DOI] [PubMed] [Google Scholar]
  • [10].Ronneberger O, Fischer P, and Brox T, “U-Net: convolutional networks for biomedical image segmentation,” in [Medical Image Computing and Computer-Assisted Intervention (MICCAI)], 234–241 (2015).
  • [11].Huo Y, Xu Z, Xiong Y, Aboud K, Parvathaneni P, Bao S, Bermudez C, Resnick SM, Cutting LE, and Landman BA, “3D whole brain segmentation using spatially localized atlas network tiles,” NeuroImage 194, 105–119 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [12].Huo Y, Plassard AJ, Carass A, Resnick SM, Pham DL, Prince JL, and Landman BA, “Consistent cortical reconstruction and multi-atlas brain segmentation,” NeuroImage 138, 197–210 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Shock NW, Greulich RC, Costa PT Jr, Andres R, Lakatta EG, Arenberg D, and Tobin JD, “Normal human aging: the Baltimore longitudinal study of aging,” Washington, DC. US Government Printing Office. (1984). [Google Scholar]
  • [14].Singh M, Pahl E, Wang S, Carass A, Lee J, and Prince JL, “Accurate estimation of total intracranial volume in MRI using a multi-tasked image-to-image translation network,” in [Medical Imaging 2021: Image Processing ], 11596, 110–117, SPIE; (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [15].Roy S, Butman JA, and Pham DL, “Robust skull stripping using multiple MR image contrasts insensitive to pathology,” NeuroImage 146, 132–147 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [16].Zuo L, Dewey BE, Carass A, Liu Y, He Y, Calabresi PA, and Prince JL, “Information-based disentangled representation learning for unsupervised MR harmonization,” in [Information Processing in Medical Imaging ], 346–359 (2021).
  • [17].Zuo L, Dewey BE, Liu Y, He Y, Newsome SD, Mowry EM, Resnick SM, Prince JL, and Carass A, “Unsupervised MR harmonization by learning disentangled representations using information bottleneck theory,” NeuroImage 243, 118569 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [18].Pinheiro J, Bates D, DebRoy S, Sarkar D, and R Core Team, nlme: Linear and Nonlinear Mixed Effects Models (2019). R package version 3.1–140.
  • [19].Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, and Gee JC, “N4ITK: improved N3 bias correction,” IEEE Transactions on Medical Imaging 29(6), 1310–1320 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [20].Reinhold JC, Dewey BE, Carass A, and Prince JL, “Evaluating the impact of intensity normalization on MR image synthesis,” in [Medical Imaging 2019: Image Processing ], 10949, 109493H, SPIE; (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [21].Zhao C, Dewey BE, Pham DL, Calabresi PA, Reich DS, and Prince JL, “SMORE: A self-supervised anti-aliasing and super-resolution algorithm for MRI using deep learning,” IEEE Transactions on Medical Imaging 40(3), 805–817 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [22].Zhao C, Shao M, Carass A, Li H, Dewey BE, Ellingsen LM, Woo J, Guttman MA, A. M. B., Stone, M., Calabresi, P. A., Halperin, H., and Prince, J. L., “Applications of a deep learning method for anti-aliasing and super-resolution in MRI,” Mag. Reson. Im 64, 132–141 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [23].Fonov VS, Evans AC, McKinstry RC, Almli CR, and Collins DL, “Unbiased nonlinear average age-appropriate brain templates from birth to adulthood,” NeuroImage 47, S102 (2009). [Google Scholar]
  • [24].Kingma DP and Ba J, “Adam: a method for stochastic optimization,” (2014).
  • [25].Bazin P-L and Pham DL, “Topology correction of segmented medical images using a fast marching algorithm,” Computer Methods and Programs in Biomedicine 88(2), 182–190 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [26].Royle NA, Valdés Hernández M, Muñoz Maniega S Arabisala BS, Bastin ME, Deary IJ, and Wardlaw JM, “Influence of thickening of the inner skull table on intracranial volume measurement in older people,” Magn Reson Imaging 31(6), 918–922 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [27].Caspi Y, Brouwer RM, Schnack HG, van de Nieuwenhuijzen ME, Cahn W, Kahn RS, Niessen WJ, van der Lugt A, and Pol HH, “Changes in the intracranial volume from early adulthood to the sixth decade of life: A longitudinal study,” NeuroImage 220, 116842 (2020). [DOI] [PubMed] [Google Scholar]

RESOURCES