Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2024 Sep 1.
Published in final edited form as: Proc IEEE Int Symp Biomed Imaging. 2023 Sep 1;2023:10.1109/isbi53787.2023.10230418. doi: 10.1109/isbi53787.2023.10230418

INTEGRATING PROSTATE SPECIFIC ANTIGEN DENSITY BIOMARKER INTO DEEP LEARNING PROSTATE MRI LESION SEGMENTATION MODELS

Jiayang Zhong 1, Lawrence H Staib 1,2,3, Rajesh Venkataraman 5, John A Onofrey 1,2,4
PMCID: PMC10711801  NIHMSID: NIHMS1949921  PMID: 38090633

Abstract

Prostate cancer lesion segmentation in multi-parametric magnetic resonance imaging (mpMRI) is crucial for pre-biopsy diagnosis and targeted biopsy guidance. Deep convolution neural networks have been widely utilized for lesion segmentation. However, these methods fail to achieve a high Dice coefficient because of the large variations in lesion size and location within the gland. To address this problem, we integrate the clinically-meaningful prostate specific antigen density (PSAD) biomarker into the deep learning model using feature-wise transformations to condition the features in latent space, and thus control the size of lesion prediction. We tested our models on a public dataset with 214 annotated mpMRI scans and compared the segmentation performance to a baseline 3D U-Net model. Results demonstrate that integrating the PSAD biomarker significantly improves segmentation performance in both Dice coefficient and centroid distance metric.

Index Terms—: Prostate lesion segmentation, Bi-parametric MRI, Prostate Specific Antigen Density, Feature-wise transformation

1. INTRODUCTION

Prostate cancer (PCa) is the second leading cause of cancer mortality in men, and in 2022, 27% of all cancer in men is prostate cancer [1]. However, PCa is often over-treated and traditional diagnosis of PCa often involves repeated needle biopsy, which increases the risk of infection [2, 3]. Therefore, non-invasive methods to identify and diagnose PCa are critical to reduce unnecessary biopsies. Multi-parametric magnetic resonance imaging (mpMRI) of the prostate is becoming more routinely used for PCa diagnosis [4]. mpMRI provides both anatomical imaging and functional imaging sequences for radiologists to make non-invasive diagnoses [5, 6]. Additionally, pre-biopsy mpMRI can also be used to locate lesions for needle biopsy targeting [7]. As a result of increased use of pre-biopsy prostate MRI, the demand for accurate PCa delineation is rising, but human labeling of PCa in mpMRI scans is time consuming and depends on training and experience [8]. Wide inter-observer variation is also reported, two manual segmentations may only have moderate agreement with a Dice coefficient of 0.48–0.52 [9].

To address problems of human delineation and increase the consistency between segmentations, deep learning-based artificial intelligence methods have been developed to segment PCa lesions in MRI. Alkadi et al. proposed a 3D U-Net based method for PCa segmentation in T2-weighted (T2W) MRI [10]. Later, Chen et al. utilized mpMRI scans by introducing a multi-branch feature extraction for the U-Net [11]. Wang et al. proposed a cascaded Mask R-CNN method for dominant intraprostatic lesions segmentation to first find coarse features [12]. Similarly, Liu et al. designed a multi-scale network to retain both global information and small lesion features [13]. Duran et al. introduced an attention mechanism into PCa segmentation by proposing ProstAttention-Net [14]. However, deep learning methods fail to achieve high agreement with manual segmentation because the lesion boundary agreement (typically measured by Dice coefficient) greatly depends on the segmentation size [9], and small lesion sizes make this difficult.

To improve PCa lesion segmentation performance of deep learning methods, we integrate additional PCa biomarkers and clinical information to help with the segmentation task. Prostate specific antigen (PSA) blood serum measurements and PSA density (PSAD) (calculated by dividing PSA by gland volume) are important biomarkers in PCa screening and diagnosis. PCa will cause a person’s PSA level to rise and PSAD is predictive of metastatic disease [15]. We also include patient age in our study. As age increases, PSA levels tend to rise, and the likelihood of being diagnosed with high-risk PCa also increases [16]. In this study, we integrate PSAD and and age into a deep neural network using feature-wise transformations (FWTs) [17]. Here, FWTs act to condition the network to this additional clinical information.

The contributions of this work are threefold: (i) we propose a method to integrate clinical biomarkers into a U-Net for prostate lesion segmentation; (ii) we show that including PSAD significantly improves the segmentation performance for prostate lesion; and (iii) we test multiple FWT strategies within the U-Net to show that channel-wise multiplication is the best way to include PSAD and that the bottleneck layer is the best location to apply these transformations.

2. METHODS

2.1. Dataset

Models in this work were trained and evaluated on the Public Training and Development Dataset from the PI-CAI challenge [18]. The dataset consists of 1,500 bi-parametric MRI (bpMRI) scans (T2W and ADC sequences) acquired at three sites. Of these, 220 cases were annotated by a human expert and 214 annotated scans are provided with PSA and patient age information. The dataset contains AI-derived whole-gland prostate segmentation masks created using an algorithm validated to have mean Dice similarity of 0.90. The 214 scans included in this study contain 230 lesions: 104 in the peripheral zone and 126 in the central gland; and 68 in the base, 77 in the mid-gland, 85 in the apex, and 2 outside the whole-gland mask. PSAD values are calculated by dividing PSA by the AI-derived prostate volume. We split the dataset into independent training, validation, and testing sets (Table 1).

Table 1.

Cohort clinical information (mean±SD).

Training Validation Testing
n 128 43 43
PSA (ng/ml) 14.1±10.7 16.5±11.6 16.1±17.5
PSAD (ng/ml2) 0.3±0.3 0.4±0.3 0.4±0.4
Age (years) 67.0±6.6 65.7±6.2 66.9±6.3
Open in a new tab

2.2. Feature-wise Transformation

The architecture of the model used in this work is 3D U-Net [19]. Rather than attempting to demonstrate state-of-the-art segmentation performance [20], here, we focus on studying the effects of FWT on a standard U-net architecture.

In order to find the best strategy to integrate biomarkers (PSAD) into the segmentation U-Net, we applied FWTs in four different ways (Fig. 1): (1) directly multiply the PSAD scalar with the encoder features to control the feature globally; (2) use a multi-layer perceptron (MLP) to fan out the PSAD scalar into a vector of the same size as the number of feature channels, and then multiply the vector with the feature to individually control each channel; (3) use a MLP to fan out the PSAD scalar into a tensor of the same size as the feature, and then multiply the tensor with the features; and (4) use a MLP to fan out the PSAD scalar into a tensor and concatenate with the original feature as an additional channel. And we apply these FWTs at two different locations: (1) at the bottleneck of the U-Net to only scale the most compressed features, (2) at the end of every encoder block to scale all the low level features. Because the size of features at early stage of the U-Net is relatively large compared to the feature at the bottleneck, which will greatly increase the number of parameters in the MLPs of the third approach, we limit testing to the bottleneck layer.

Fig. 1.

Fig. 1.

Open in a new tab

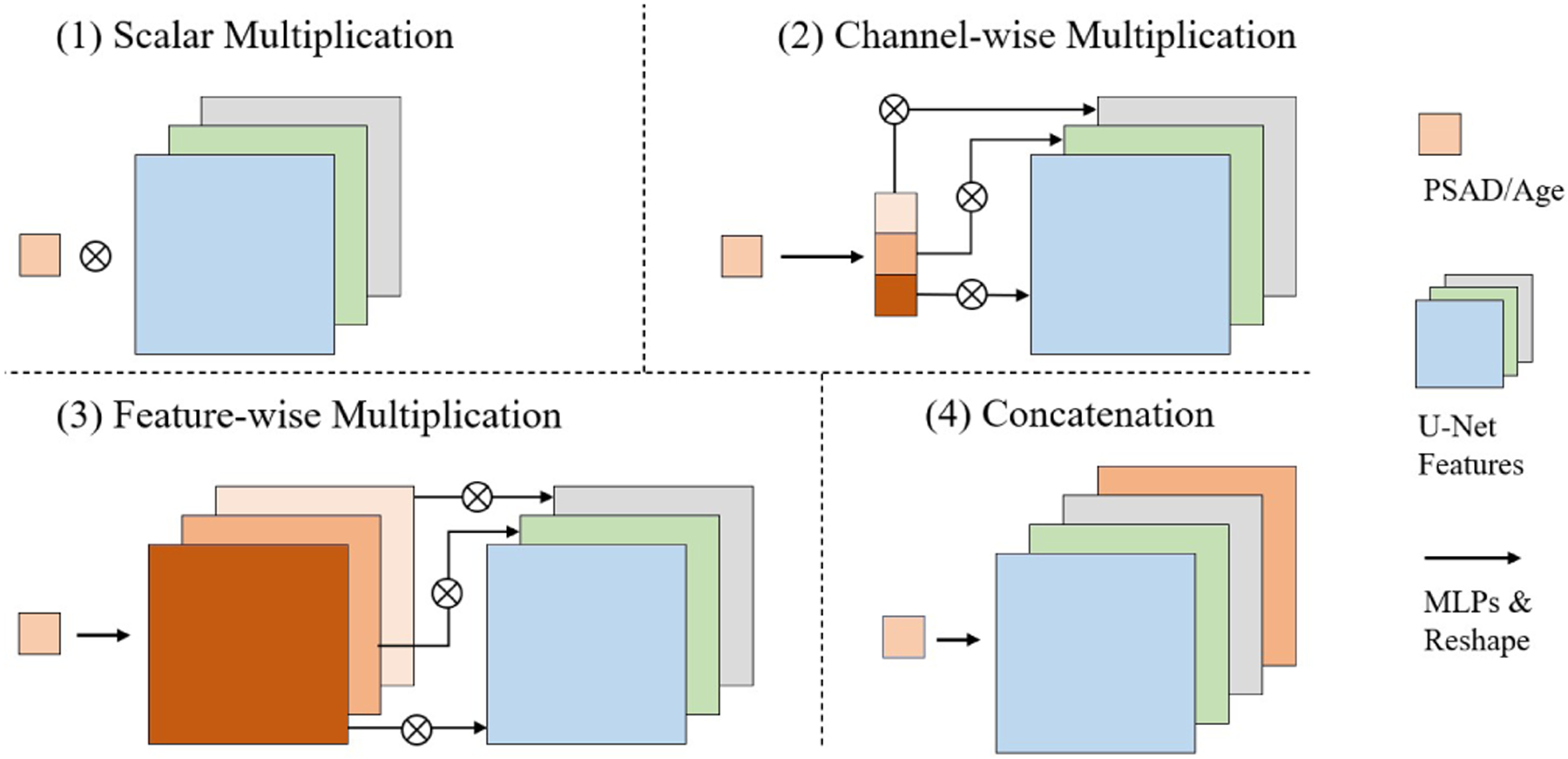
Different feature-wise transformation approaches.

In addition to PSAD, we also include patient age as additional clinical information. Here, we add age as a scalar value as an extra input to the MLP to the model with the best performance in the PSAD only test, and we compare two results.

3. EXPERIMENTS AND RESULTS

3.1. Implementation

The segmentation network input is two-channel bpMRI. All 214 bpMRI scans were first co-registered and then resampled to a voxel spacing of 1 × 1 × 3.6 mm3 as suggested by the dataset provider [21]. Then all scans were cropped into 160 × 160 × 32 around the AI-derived whole gland masks and intensities were scaled from [25th percentile of original intensity, 75th percentile of original intensity] to [−0.5, 0.5].

The model used in this work was modified based on the Dynamic U-Net from the MONAI (v0.9.0) framework. We used four encoder/decoder blocks with anisotropic strides in the z-axis to best preserve the small lesion structure in different encoder blocks. All models were implemented using PyTorch (v1.9.0) and PyTorch Lightning (v1.4.2) framework and trained on an NVIDIA P5000 GPU with Adam optimizer [22] with a batch size of 2. Random flipping along x-axis with 0.5 probability was applied during training. Argmax was applied to the output logits to generate the final binary segmentation and no additional post-processsing was performed. We adopted generalized Dice loss as the loss function since it is especially designed for imbalanced datasets by weighting each class by the inverse size of the region [23]. Training converged around 1,500 epochs.

3.2. Evaluation

We quantitatively evaluated our results using both Dice coefficient and centroid distance on a holdout testing set of 43 scans. If there are two models that both completely miss the ground truth and report a Dice of 0, radiologists may be more interested in the model that provides a closer guess to the ground-truth lesion. In this case, Dice may fail to measure the performance. To solve the problem and better evaluate our models, we adopt centroid distance as a complementary metric. Centroid distance measures the minimum euclidean distance between the centers of gravity of a ground-truth lesion and all predicted lesion blobs, so it is more informative when we care about the location of the prediction instead of the volume.

Table 2 summarizes the experimental results. The baseline method with 3D Dynamic U-Net from MONAI demonstrated a mean Dice of 0.28. Compared to this baseline, all FWT approaches improved the performance of the model by integrating extra biomarkers and clinical information to the network. Among all FWT approaches, channel-wise multiplication achieves the best performance, significantly improving mean Dice by 28% to 0.36 (p<0.05, paired t-test) and slightly decreased the mean centroid distance between the ground-truth and prediction compared to the baseline model (Fig. 2). The channel-wise multiplication approach is also tested with both PSAD and patient age as input, but the performance of the model decreased. Compared to the single scalar multiplication methods, the channel-wise approach puts weights on each channel to scale the contribution of each filter in the U-Net instead of simply conditioning all the features globally; compared to the feature-wise approach, the PSAD value may not provide enough information to scale every element in the feature. In addition, the concatenation method may not fit into this U-Net-based model because the number of features at the bottleneck of a U-Net is larger for 3D models and there is no cross-channel information exchange. As a result, the extra PSAD channel has small contributions to the final layer.

Table 2.

Comparisons of different feature-wise transformations approaches, the unit of centroid distance is the number of voxels

Bottleneck Every encoder block
Dice Centroid Dist Dice Centroid Dist
Baseline 0.28±0.25 9.49±7.38 N/A N/A
PSAD Scalar mul 0.35±0.27 9.73±10.22 0.32±0.27 10.66±11.57
Channel wise mul 0.36±0.25 8.65±7.62 0.34±0.23 8.65±7.62
Feature wise mul 0.33±0.27 10.89±11.36 N/A N/A
Concatenate 0.39±0.26 9.88±9.77 0.34±0.27 10.57±10.99
PSAD + Age Channel wise mul 0.31±0.25 11.87±13.24 0.31±0.27 12.26±13.54
Open in a new tab

Fig. 2.

Fig. 2.

Open in a new tab

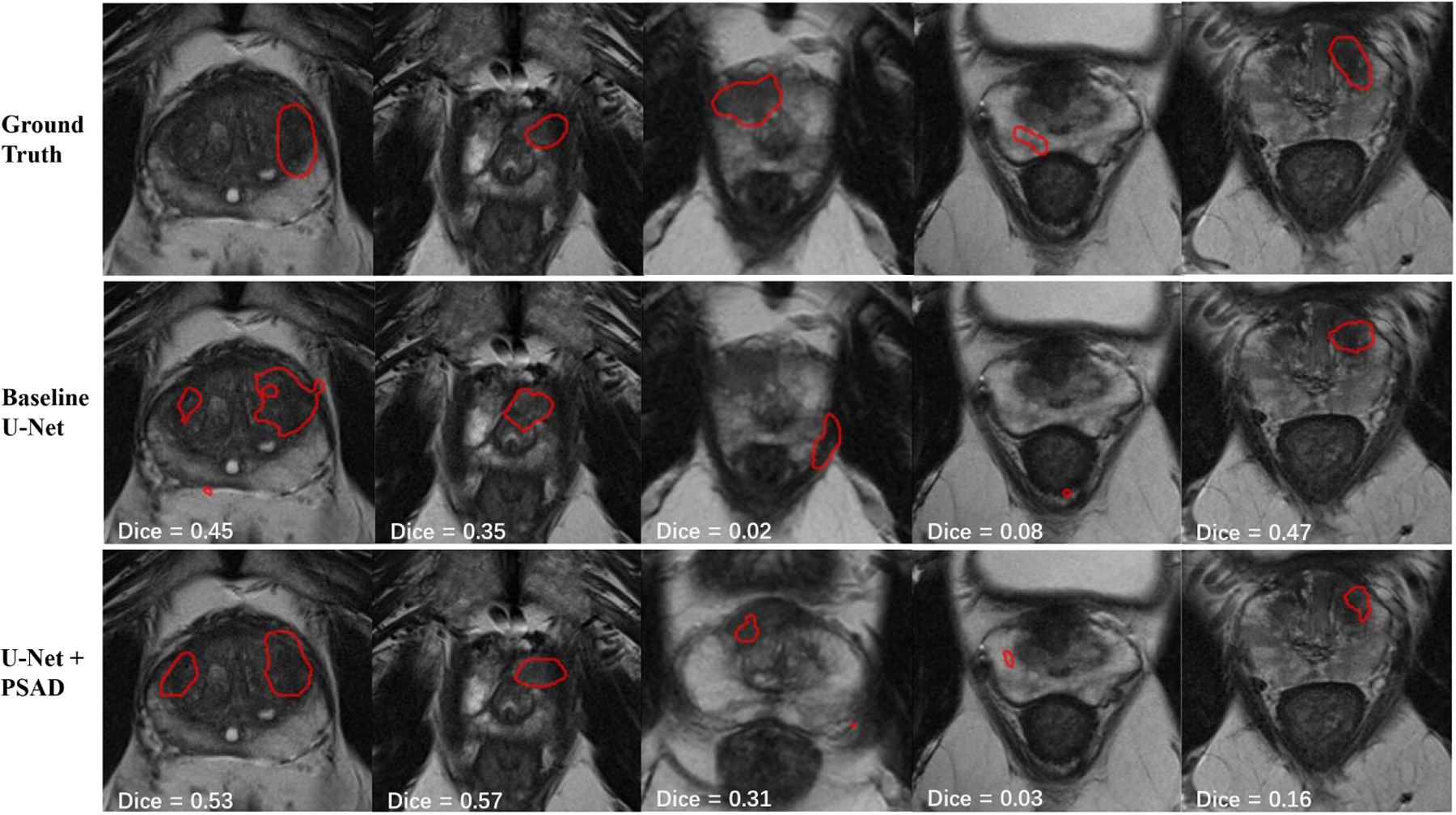
Example segmentation results of baseline U-Net and U-Net with channel-wise FWT. In the first 3 cases U-Net with FWT demonstrates predictions that have both better boundary and closer distance to the ground truth. In the 4th case, both models fail to achieve a high Dice while the FWT model gives a closer prediction to the ground truth. In the 5th case, FWT gives a worse prediction but still locates the lesion.

For FWT location, our results showed that the bottleneck is the better layer to include this mechanism. Features are most compressed at the bottleneck, so adding biomarker information there as a constraint is most effective, while adding information at the early stages of the encoder may be too strong of a constraint for the model. The comparison between the PSAD only and PSAD + age indicates that PSAD by itself is a better biomarker when integrated into the neural network.

3.3. PSAD ablation study

To further examine the effectiveness of the PSAD biomarkers in the channel-wise transformation approach, we conducted a study by manually changing the PSAD value. In this study, we chose to do our tests on a bpMRI scan with relatively large PCa, so that the Dice coefficient will not be too sensitive to small centroid shifts and the change in lesion prediction volume can be best observed. Because PSAD level tends to rise as PCa develops, we hypothesized that the PSAD value can control the size of the final prediction. The PSAD value of the selected case is 0.43. We incrementally adjusted the PSAD within the range [0, 1], and then examined the change in Dice and volume of the predictions.

The performance and volume of the prediction segmentation both increased as PSAD value increased from 0 to 0.5 (Fig. 3), the segmentation volume stops increasing as PSAD value increases from 0.5 to 1.0. When PSAD value is 0, the prediction volume dropped to 76% of the prediction with original PSAD of 0.43. In Addition, we set PSAD values for all cases to 0 and the mean prediction volume of our test set dropped from 4071 voxels to 3805, and when we set PSAD values for cases to 1, mean prediction volume increased to 4813 voxels. These results indicate that the PSAD is able to scale the features and control the actual size of prediction output of our model in a clinically-realistic manner.

Fig. 3.

Fig. 3.

Open in a new tab

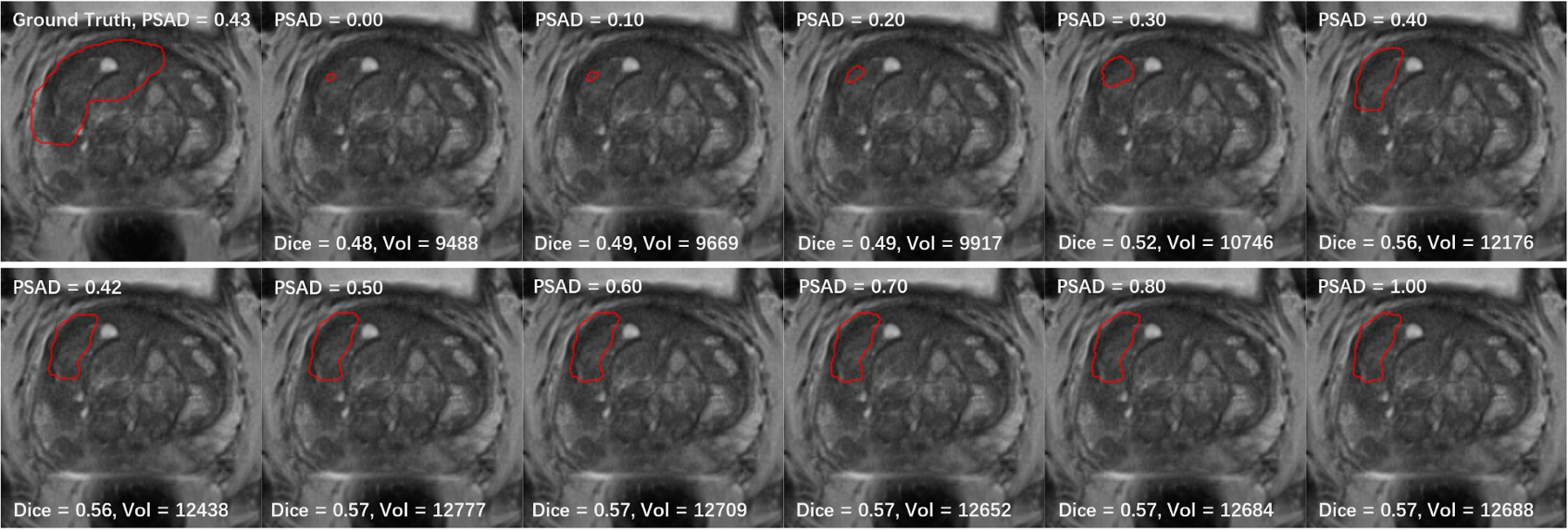
Dice coefficient and prediction volume (total number of pixels) for different PSAD values, tested on a case with PSAD of 0.43.

4. CONCLUSION

In this paper, we utilized FWTs to integrate biomarkers (PSAD) and clinical information (patient age) into a deep learning PCa segmentation model. Our experiments showed that the additional information can significantly improve segmentation performance compared to models without these features. Furthermore, we examined different FWT approaches and locations within the network to apply the transformations. We showed that the best approach is to use a MLP to expand the biomarker scalar into a vector to multiply the features channel-wise, and the best location to add extra information is at the bottleneck layer, because features are most compressed at bottleneck in a U-Net so the biomarker information can be easily applied; and PSAD performs better than patient age for the PCa segmentation task. Finally, we showed that PSAD is able to control the size of output prediction by scaling the latent features. A limitation of this work is that we assume availability of a gland mask; however, whole gland segmentation is a relatively easier task and is a routine part of clinical systems such as ProFuseCAD (Eigen Health, Grass Valley, CA) and this is only used to for coarse localization of the gland region to remove background anatomy.

However, there are still problems to be solved. Firstly, mean Dice coefficient for our model is 0.36, which may not outperform state-of-art segmentation methods. Our focus for this paper is to demonstrate that additional biomarkers are able to help with the segmentation task instead of trying to propose a best model, but in the future, we will still need to improve the model for real-world clinical use. Thanks to the simplicity of FWTs, we can easily integrate this mechanism into other state-of-art models such as nnU-net [20] to improve performance. Secondly, the PSAD values used in this study were derived from AI-based whole prostate segmentations, so even though the algorithm for whole gland segmentation performs well with a Dice of 0.90, errors may still exist. While small deviations in PSAD caused by gland segmentation errors may not have clinically-meaningful impact, in the future, we would like to add noise to the PSAD values during the training process to model this variation and to increase the robustness of model. Finally, our method is currently tested on a single public dataset, and we would like to validate our methods on external datasets in the future.

ACKNOWLEDGMENTS

This work was supported by National Institute of Health (NIH) National Cancer Institute (NCI) R42 CA224888.

Footnotes

COMPLIANCE WITH ETHICAL STANDARDS

This research study was conducted retrospectively using human subject data made available in open access by [18]. Ethical approval was not required as confirmed by the license attached with the open access data.

REFERENCES

  • [1].Siegel Rebecca L, Miller Kimberly D, Fuchs Hannah E, and Jemal Ahmedin, “Cancer statistics, 2022,” CA Cancer J. Clin, vol. 72, no. 1, pp. 7–33, Jan. 2022. [DOI] [PubMed] [Google Scholar]
  • [2].Borghesi Marco, Ahmed Hashim, Nam Robert, Schaeffer Edward, Schiavina Riccardo, Taneja Samir, Weidner Wolfgang, and Loeb Stacy, “Complications after systematic, random, and image-guided prostate biopsy,” European urology, vol. 71, no. 3, pp. 353–365, 2017. [DOI] [PubMed] [Google Scholar]
  • [3].Sung Hyuna, Ferlay Jacques, Siegel Rebecca L, Laversanne Mathieu, Soerjomataram Isabelle, Jemal Ahmedin, and Bray Freddie, “Global cancer statistics 2020: Globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries,” CA: a cancer journal for clinicians, vol. 71, no. 3, pp. 209–249, 2021. [DOI] [PubMed] [Google Scholar]
  • [4].Suarez-Ibarrola Rodrigo, Sigle August, Eklund Martin, Eberli Daniel, Miernik Arkadiusz, Benndorf Matthias, Bamberg Fabian, and Gratzke Christian, “Artificial intelligence in magnetic resonance imaging–based prostate cancer diagnosis: Where do we stand in 2021?,” European Urology Focus, 2021. [DOI] [PubMed] [Google Scholar]
  • [5].Weinreb Jeffrey C, Barentsz Jelle O, Choyke Peter L, Cornud Francois, Haider Masoom A, Macura Katarzyna J, Margolis Daniel, Schnall Mitchell D, Shtern Faina, Tempany Clare M, Thoeny Harriet C, and Verma Sadna, “PI-RADS prostate imaging – reporting and data system: 2015, version 2,” Eur. Urol, vol. 69, no. 1, pp. 16–40, Jan. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [6].Eldred-Evans David, Burak Paula, Connor Martin J, Day Emily, Evans Martin, Fiorentino Francesca, Gammon Martin, Hosking-Jervis Feargus, Klimowska-Nassar Natalia, McGuire William, et al. , “Population-based prostate cancer screening with magnetic resonance imaging or ultrasonography: the ip1-prostagram study,” JAMA oncology, vol. 7, no. 3, pp. 395–402, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [7].Onofrey John A, Staib Lawrence H, Sarkar Saradwata, Venkataraman Rajesh, Nawaf Cayce B, Sprenkle Preston C, and Papademetris Xenophon, “Learning non-rigid deformations for robust, constrained point-based registration in Image-Guided MR-TRUS prostate intervention,” Med. Image Anal, vol. 39, pp. 29–43, July 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [8].Rosenkrantz Andrew B, Kim Sooah, Lim Ruth P, Hindman Nicole, Deng Fang-Ming, Babb James S, and Taneja Samir S, “Prostate cancer localization using multiparametric mr imaging: comparison of prostate imaging reporting and data system (pi-rads) and likert scales,” Radiology, vol. 269, no. 2, pp. 482–492, 2013. [DOI] [PubMed] [Google Scholar]
  • [9].Schelb Patrick, Tavakoli Anoshirwan Andrej, Tubtawee Teeravut, Hielscher Thomas, Radtke Jan-Philipp, Görtz Magdalena, Schuetz Viktoria, Kuder Tristan Anselm, Schimmoeller Lars, Stenzinger Albrecht, et al. , “Comparison of prostate mri lesion segmentation agreement between multiple radiologists and a fully automatic deep learning system,” in RöFo-Fortschritte auf dem Gebiet der Röntgenstrahlen und der bildgebenden Verfahren. Georg Thieme; Verlag KG, 2021, vol. 193, pp. 559–573. [DOI] [PubMed] [Google Scholar]
  • [10].Alkadi Ruba, Taher Fatma, El-Baz Ayman, and Werghi Naoufel, “A deep learning-based approach for the detection and localization of prostate cancer in t2 magnetic resonance images,” Journal of digital imaging, vol. 32, no. 5, pp. 793–807, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [11].Chen Yizheng, Xing Lei, Yu Lequan, Bagshaw Hilary P, Buyyounouski Mark K, and Han Bin, “Automatic intraprostatic lesion segmentation in multiparametric magnetic resonance images with proposed multiple branch unet,” Medical physics, vol. 47, no. 12, pp. 6421–6429, 2020. [DOI] [PubMed] [Google Scholar]
  • [12].Wang Tonghe, Lei Yang, Abiodun Ojo Olayinka A, Akin-Akintayo Oladunni A, Akintayo Akinyemi A, Curran Walter J, Liu Tian, Schuster David M, and Yang Xiaofeng, “Mri-based prostate and dominant lesion segmentation using deep neural network,” in Medical Imaging 2021: Computer-Aided Diagnosis. SPIE, 2021, vol. 11597, pp. 376–381. [Google Scholar]
  • [13].Liu Yatong, Zhu Yu, Wang Wei, Zheng Bingbing, Qin Xiangxiang, and Wang Peijun, “Multi-scale discriminative network for prostate cancer lesion segmentation in multiparametric mr images,” Medical Physics, 2022. [DOI] [PubMed] [Google Scholar]
  • [14].Duran Audrey, Dussert Gaspard, Rouvière Olivier, Jaouen Tristan, Jodoin Pierre-Marc, and Lartizien Carole, “Prostattention-net: A deep attention model for prostate cancer segmentation by aggressiveness in mri scans,” Medical Image Analysis, vol. 77, pp. 102347, 2022. [DOI] [PubMed] [Google Scholar]
  • [15].Bruno Salvatore M, Falagario Ugo G, d’Altilia Nicola, Recchia Marco, Mancini Vito, Selvaggio Oscar, Sanguedolce Francesca, Del Giudice Francesco, Maggi Martina, Ferro Matteo, et al. , “Psa density help to identify patients with elevated psa due to prostate cancer rather than intraprostatic inflammation: a prospective single center study,” Frontiers in Oncology, p. 1845, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [16].Bechis Seth K, Carroll Peter R, and Cooperberg Matthew R, “Impact of age at diagnosis on prostate cancer treatment and survival,” Journal of Clinical Oncology, vol. 29, no. 2, pp. 235, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [17].Dumoulin Vincent, Perez Ethan, Schucher Nathan, Strub Florian, de Vries Harm, Courville Aaron, and Bengio Yoshua, “Feature-wise transformations,” Distill, vol. 3, no. 7, pp. e11, 2018. [Google Scholar]
  • [18].Saha Anindo, Twilt Jasper Jonathan, Bosma Joeran Sander, van Ginneken Bram, Yakar Derya, Elschot Mattijs, Veltman Jeroen, Fütterer Jurgen, de Rooij Maarten, and Huisman Henkjan, “Artificial Intelligence and Radiologists at Prostate Cancer Detection in MRI: The PI-CAI Challenge,” 2022.
  • [19].Ronneberger Olaf, Fischer Philipp, and Brox Thomas, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241. [Google Scholar]
  • [20].Isensee Fabian, Jaeger Paul F, Kohl Simon AA, Petersen Jens, and Maier-Hein Klaus H, “nnu-net: a self-configuring method for deep learning-based biomedical image segmentation,” Nature methods, vol. 18, no. 2, pp. 203–211, 2021. [DOI] [PubMed] [Google Scholar]
  • [21].Bosma Joeran S, Saha Anindo, Hosseinzadeh Matin, Slootweg Ilse, de Rooij Maarten, and Huisman Henkjan, “Report-guided automatic lesion annotation for deep learning-based prostate cancer detection in bpmri,” arXiv preprint arXiv:2112.05151, 2021. [Google Scholar]
  • [22].Kingma Diederik P and Ba Jimmy, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
  • [23].Sudre Carole H., Li Wenqi, Vercauteren Tom, Ourselin Sébastien, and Cardoso M. Jorge, “Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations,” CoRR, vol. abs/1707.03237, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES