Abstract
Efficacy of deep brain stimulation (DBS) for motor signs of Parkinson’s disease (PD) depends in part on post-operative programming of stimulus parameters. There is a need for a systematic approach to tuning parameters based on patient physiology. We used a physiologically realistic computational model of the basal ganglia network to investigate the emergence of a 34 Hz oscillation in the PD state and its optimal suppression with DBS. Discrete time transfer functions were fit to post-stimulus time histograms (PSTHs) collected in open-loop, by simulating the pharmacological block of synaptic connections, to describe the behavior of the basal ganglia nuclei. These functions were then connected to create a mean-field model of the closed-loop system, which was analyzed to determine the origin of the emergent 34 Hz pathological oscillation. This analysis determined that the oscillation could emerge from the coupling between the globus pallidus external (GPe) and subthalamic nucleus (STN). When coupled, the two resonate with each other in the PD state but not in the healthy state. By characterizing how this oscillation is affected by subthreshold DBS pulses, we hypothesize that it is possible to predict stimulus frequencies capable of suppressing this oscillation. To characterize the response to the stimulus, we developed a new method for estimating phase response curves (PRCs) from population data. Using the population PRC we were able to predict frequencies that enhance and suppress the 34 Hz pathological oscillation. This provides a systematic approach to tuning DBS frequencies and could enable closed-loop tuning of stimulation parameters.
Keywords: basal ganglia, deep brain stimulation, Parkinson’s disease, parameter tuning, computational model, oscillations, phase-response curves
1. Introduction
Deep brain stimulation (DBS) is used to treat motor signs of medication-refractory Parkinson’s disease (PD). Currently, stimulation parameters are tuned post-operatively by a clinician using a trial-and-error process (Green and Aziz, 2014; Volkmann et al., 2002). There is a need for a systematic approach for tuning DBS parameters based on patient physiology. Depending on how pathological oscillations emerge, we hypothesize that it is possible to determine DBS parameters which are optimized for disrupting oscillations. In this paper we first study the origins of these oscillations using a simplified systems-level model of basal ganglia nuclei. Then, we present a systematic method for tuning DBS frequency and test it in a network model of PD. While these theories are tested in a computational model, the analysis can be applied to local field recordings measured in non-human primates or humans.
In the first part of this paper the goal is to demonstrate how a systems-level mean field model of the basal ganglia can be used to determine how pathological oscillations emerge (Section 2). In the second part, we will measure PRCs from the population oscillation with the goal to predict subject-specific optimal stimulus frequencies to maximize suppression of the oscillation (Section 3). These methods will be tested using a physiologically realistic computational model of the basal ganglia network developed by Hahn and McIntyre (Hahn and McIntyre, 2010).
2. Origins of Pathological Oscillations
The basal ganglia network is responsible for preparing and initiating movement (Alexander et al., 1986; DeLong et al., 1992). In PD, this network is altered due to the loss of dopaminergic input from the substantia nigra (Bernheimer et al., 1973). This leads to changes in the firing rates and the emergence of increased oscillatory activity, particularly in the beta frequency range (13-35 Hz) (Brown, 2006; Hammond et al., 2007). Beta oscillations are seen in the three nuclei modeled in the Hahn and McIntyre model: the GPe, GPi, and STN (Brown, 2006). It is hypothesized that beta oscillations are responsible for anti-kinetic motor signs of PD (Bhidayasiri and Truong, 2008), and that DBS works by disrupting these oscillations (Bronte-Stewart et al., 2009; Kuhn et al., 2008; McConnell et al., 2012; Meissner et al., 2005).
Pathological oscillations seen in PD could arise in various ways: 1) as periodic drive from an external source, such as the cortex, which is patterned onto the basal ganglia network; 2) as a synchronous population of neurons in the basal ganglia firing periodically at the beta frequency; or 3) as an emergent property of the basal ganglia network. Recordings of neurons in STN, GPe, and GPi show bursting behavior in the beta frequency range under PD conditions, but the neurons do not show highly precise spike synchrony, suggesting that it is unlikely the oscillations are due to synchronous firing of a single population of neurons (Hashimoto et al., 2003; Mallet et al., 2008). There is evidence both supporting and refuting the hypotheses that the oscillation arises from the cortex or that the oscillation is generated within the basal ganglia (Bevan and Wilson, 1999; Brown and Williams, 2005; Courtemanche et al., 2003; Dejean et al., 2009; Goldberg et al., 2004; Gradinaru et al., 2009; Hammond et al., 2007; Holgado et al., 2010; Kuhn et al., 2005; McCarthy et al., 2011; Moran et al., 2011; Nevado-Holgado et al., 2014; Pasillas-Lépine, 2013; Plenz and Kital, 1999; Sharott et al., 2005; Terman et al., 2002).
In this paper, we will test the hypothesis that pathological oscillations in PD emerge in the GPe-STN feedback loop within the basal ganglia network. We will use a computational model to show how this loop can be the origin of this emergent pathological oscillation.
The GPe-STN loop is composed of excitatory glutamatergic projections from STN to GPe, and inhibitory GABAergic projections from GPe back onto STN (Albin et al., 1989). This loop makes the system conducive to generating oscillations (Bevan et al., 2002; Marreiros et al., 2012). Many physiologically realistic computational models of the basal ganglia exist to model parkinsonian oscillations (Gillies and Willshaw, 2007; Hahn and McIntyre, 2010; Leblois et al., 2006; Terman et al., 2002). However, even when these models can reproduce oscillations, the complexity of the models makes it difficult to understand how the oscillations emerge. In this paper we use a simplified mean-field model fit to the data from a complex network model to understand how changes caused by dopamine depletion result in the propensity of the network to oscillate.
2.1. Physiologically Realistic Computational Model of Basal Ganglia Oscillations: Hahn and McIntyre Model
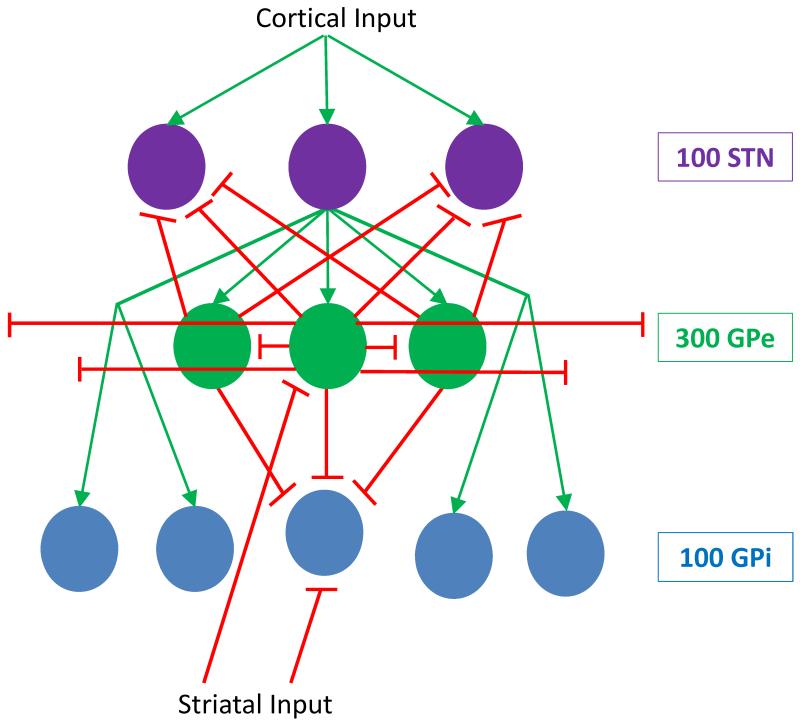
In this work we used a physiologically realistic computational model of DBS to the subthalamic nucleus (STN) developed by Hahn and McIntyre (Hahn and McIntyre, 2010). The model simulates individual neurons within the basal ganglia and produces a set of spike times from these neurons. The model can be downloaded at http://senselab.med.yale.edu/modeldb. The model contains 500 single-compartment conductance-based neurons: 100 STN neurons, 100 globus pallidus internal (GPi), and 300 globus pallidus external (GPe) neurons. Input spike trains from the cortex and striatum are also included. The neurons are synaptically coupled in a physiologically realistic way, illustrated in Figure 1. Data from non-human primates given MPTP, a drug commonly used to induce parkinsonian symptoms in primates (Jenner, 2003, 2008; Langston et al., 1983), were used to fit the model. Parameters were changed until the output of each nucleus matched experimental data to simulate a healthy state. DBS was simulated by activating STN efferent paths as well as applying a direct subthreshold current to the soma of STN cells. All simulations were run using NEURON (Hines and Carnevale, 1997, 2001). While there are other network models of the basal ganglia and PD (Holgado et al., 2010; van Albada et al., 2009; van Albada and Robinson, 2009), we chose the Hahn and McIntyre model for the physiologically realistic modeling of the neurons and their connectivity. Furthermore, the model’s output can be directly compared to physiological recordings and thus can be used to design future non-human primate experiments.
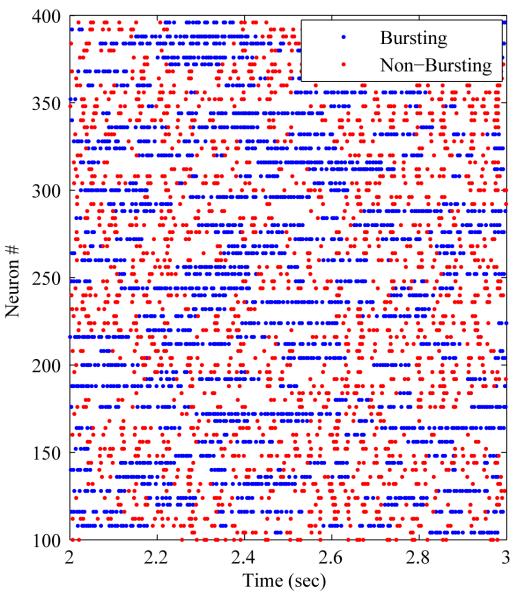
Figure 1.
Computational model of the basal ganglia fit to non-human primate data developed by Hahn and McIntyre. A: Connectivity diagram of the Hodgkin-Huxley neurons making up the network. B: The output of the computational model is spike times. A rastergram of Globus Pallidus external neurons over a small window of time are shown here where the y-axis is neuron number, and the x-axis is time (seconds). Neurons exhibit a bursting (blue) and non-bursting (red) phase classified by the spiking rate.
We made a few changes to the original model. In the Hahn and McIntyre model, the cortex provided a periodic drive at 16 Hz. However, this results in a very strong oscillation in the basal ganglia network that did not look physiological. We added a standard deviation of 5 msec to the period of this input which widened the distribution of the cortical drive and significantly decreased the harmonics of the 16 Hz signal.
First, we must characterize the emergent pathological oscillation seen in the Hahn and McIntyre model. To do this, spectral analysis of the spike times of GPe neurons was used to compare the oscillation across healthy, PD, and DBS On conditions.
2.1.1. Generating Power Spectra
To detect pathological oscillations from the spike times of the neurons in the basal ganglia network model we generated a power spectrum and looked for peaks in the spectrum. There are multiple ways to calculate the power spectrum from spike time data. One approach is to calculate the power spectrum by Fourier transforming the autocorrelation spike density. However, in this approach, the instantaneous phase of the oscillation at a particular time cannot be calculated. Another approach to estimate the power spectrum is to use a truncated point process Fourier transform of the spikes. The spike train can be represented as the sum of delta functions , where ki represents the time of the ith spike in the network. The Fourier transform of the spike train can be calculated as , where and ω = 2πf and f is the frequency at which the spike train is Fourier transformed. However, because s(t) is zero, except at the spike times, this can also be calculated as . The truncated Fourier transform was calculated over a range of 0-100 Hz. From the Fourier transform it is then possible to estimate the instantaneous phase and amplitude of the population oscillation at any given time from the spikes of the individual neurons, described below.
2.1.2. Pathological Beta Oscillations
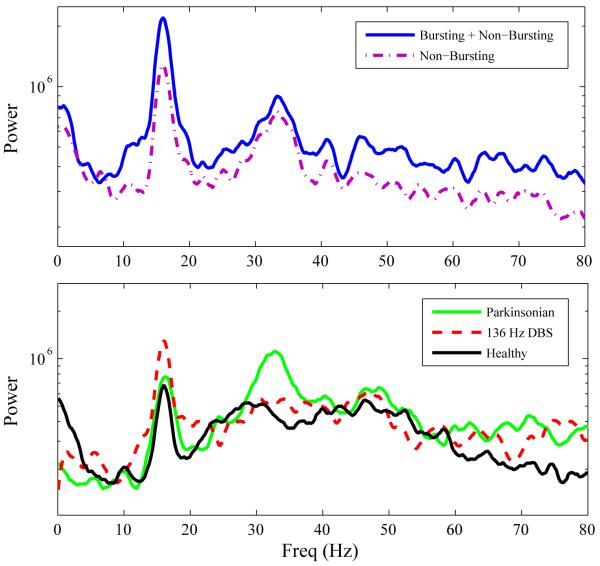
Spectral analysis of the spike times of the GPe neurons revealed an emergent oscillation at 34 Hz in the Hahn and McIntyre model (Figure 2). This 34 Hz oscillation is not seen in the healthy state and is reduced when 136 Hz DBS-like stimulation is applied to the STN (Figure 2). Synaptic drive from the cortex was patterned onto the STN at 16Hz, raising the concern that the 34Hz oscillation was simply a harmonic. However, the 16 Hz stimulation remained consistent throughout all conditions, while the 34 Hz oscillation did not. Changing the frequency of the cortical input, for example from 16 Hz to 10 Hz, shifted the 16 Hz peak but did not shift the 34 Hz peak (data not shown). Completely removing the 16Hz drive caused 34 Hz oscillation to disappear, presumably because the excitability of the STN neurons decreased. This fits with the hypothesis that both internal and external drive is needed to generate the pathological state, and provides support for the hypothesis that oscillations are not seen in vitro due to a lack of cortical input (Bevan and Wilson, 1999). Also, increasing variability of the timing of the stimulus (stimulus interval of 62.5+/−5 msec) increased the signal-to-noise ratio of the 34 Hz oscillation.
Figure 2.
An oscillation at 34 Hz arises in the Parkinsonian (PD) state in the non-bursting phase of spiking that is suppressed with DBS. Top: Power spectrum showing the emergence of a 34 Hz oscillation. X-axis is frequency (Hz) and y-axis is power. The peak at 16 Hz is from the cortical input at that frequency. All characteristics are preserved when spikes in the bursting phase are removed (dashed line). Bottom: A 34 Hz oscillation is seen in the power spectrum of the PD state (green) that is not present in that of the healthy state (dashed). Application of 136 Hz DBS (black) suppresses the 34 Hz oscillation. The 16 Hz peak due to the cortical input is not affected across conditions.
Neurons in the model have a bursting and non-bursting phase. We classified neurons as bursting if they had a firing rate above a selected threshold. To do this, we convolved the spike times with a Gaussian kernel 4 ms wide and all spikes above a threshold of 4 were classified as bursting. We observed a periodicity to the firing in the non-bursting phase in the rastergram (Figure 1B), which was not present in the bursting phase. The power spectrum was calculated using all spikes as well as using only non-bursting spikes. The 34 Hz oscillation remained in the power spectrum of the non-bursting spikes (Figure 2), indicating that the oscillatory activity is generated by the neurons during the non-bursting phase.
2.2. Mean-Field Models
In order to determine the origin of the pathological oscillation in the Hahn and McIntyre model, we fit a discrete time mean-field model to which models population activity. The model is fit to impulse responses measured in one area in response to stimulation of a presynaptic area. By analyzing this systems-level model we were able to determine which nuclei were necessary for the emergence of the pathological oscillation
Mean-field models were first adapted to describe the cortex by Wilson and Cowan (Wilson and Cowan, 1972). These models are conducive to mathematical analysis because they reduce the dimensionality of the problem. The systems level analysis of the equations can be used to determine the necessary conditions for the system to oscillate. In these models the average firing rate of a population, for example a population of neurons within a nucleus, is modeled as a set of differential equations. These equations determine the population firing rate given the history of the population’s firing rate and its synaptic input. These population models can then be connected with different time delays and strengths. The models can then be analyzed to determine how changes in parameters affect systems-level behaviors, such as the amplitude and frequency of oscillations.
Mean-field models have previously been used to understand the origins of oscillations within the basal ganglia network. However, in order to analyze previous models the time delays were assumed equal and the system had to be linearized around a specific point (Holgado et al., 2010; van Albada et al., 2009; van Albada and Robinson, 2009). Accurate delays are important in determining the behavior of a closed-loop system and the origin of oscillations. It is possible to calculate the stability of the system with delays (Pasillas-Lépine, 2013). However, using a discrete model the analysis of the system can be done analytically and much more simply and allows for the visualization of all the poles. Here we use discrete time models with various time delays to understand their effects on the oscillatory behavior.
2.2.1. Mean-Field Modeling of the Hahn and McIntyre Model
We hypothesize that the 34 Hz pathological oscillation seen in the Hahn and McIntyre model emerges from an interaction between STN and GPe, a systems-level oscillation. A mean field model of STN and GPe was made by fitting a function to the spike timing of the neurons. Models of the different basal ganglia nuclei were generated by measuring the stimulus triggered histogram of the post synaptic population’s response to a stimulus applied to the pre-synaptic population. This was done in open-loop, where all connections except the one connecting the pre-synaptic population to the post-synaptic populations were cut to avoid any interactions between the two populations or a separate population. This can easily be done in a computational model, but is difficult to do in humans or an animal model. The open-loop models for both nuclei are then combined to make a closed-loop systems-level model.
Origins of oscillations in closed-loop systems can be determined using the Laplace transform of the stimulus response models for each area. However, time delays between nuclei are an important aspect of the system and analysis of continuous systems with time delays is difficult; in contrast, analyzing discrete time systems with delays is relatively easy (Oppenheim et al., 1996). Therefore, we fit discrete time models to spiking data from the Hahn and McIntyre model measured in open-loop. Then, we used a discrete version of the Laplace transform, the Z-transform, to make a model of the closed-loop system.
Discrete time models were fit to peristimulus time histograms, PSTH[n], measured for each basal ganglia nucleus in open-loop. Before fitting a function to the PSTH, it was normalized to describe the proportional change from the mean firing rate: . Each NPSTH was generated by averaging 120 stimulus pulses applied at 2 Hz. Transfer functions were fit to the NPSTHs to describe the time course of the response of the post-synaptic population to the stimulus applied to the presynaptic population, as well as the delays between the two populations. Combinations of damped sine and cosine waves were used for the fits:
or
Where ω is the frequency of the oscillation, γ is the dampening time constant, A is the amplitude of the response, and d is the delay between the stimulus and the response. A robust fit was used to fit the models to the data to minimize absolute values of the error over 16 msec using Matlab’s (Natick, MA) fminsearch function. Models were fit to the GPe and STN individually, in open-loop.
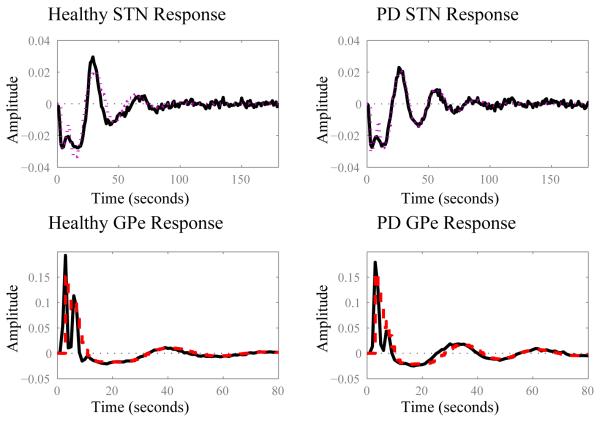
The PSTH of the STN in response to stimulation of the GPe was made in open-loop by cutting all connections except GPe to STN. The same approach was used to generate a PSTH of the GPe response to the stimulation of the STN. Transfer function fits to the normalized PSTH in the healthy and PD state are plotted in Figure 3 and the coefficients for each model are provided in Table 1.
Figure 3.
Impulse response fits to stimulus triggered histograms accurately reproduce oscillations. Black: Stimulus triggered histograms. Dashed: Impulse response fits. Top: STN response to a stimulus pulse to GPe in open loop in the healthy (left) and PD (right) state. Bottom: GPe response to a stimulus pulse in STN in the healthy (left) and PD (right) state.
Table 1.
Values used in transfer function fits. STN was fit with a cosine and sine wave under parkinsonian and healthy conditions. GPe was fit with two cosine waves under each condition.
| Frequency (ω) |
Amplitude (A) |
γ | Delay (d) |
|
|---|---|---|---|---|
| STN | ||||
|
| ||||
| Cosine | 0.1824 | −0.0297 | 0.9651 | −3 |
| Sine | 0.2236 | −0.0512 | 0.9510 | −9 |
|
| ||||
| HSTN | ||||
|
| ||||
| Cosine | 0.1555 | −0.0282 | 0.9607 | −3 |
| Sine | 0.1953 | −0.0567 | 0.9499 | −9 |
|
| ||||
| GPe | ||||
|
| ||||
| Cosine 1 | 0.2288 | 0.0445 | 0.9664 | −7 |
| Cosine 2 | 0.3357 | 0.1585 | 0.8310 | −3 |
|
| ||||
| HGPe | ||||
|
| ||||
| Cosine 1 | 0.1775 | 0.0422 | 0.9604 | −6 |
| Cosine 2 | 0.2979 | 0.1516 | 0.8204 | −3 |
2.2.2. Analyzing the Mean Field Model to Determine the Origin of the Oscillation
In the basal ganglia network the STN and GPe constitute an excitatory-inhibitory feedback loop (Albin et al., 1989). To test if the pathological oscillation emerges from this loop, we analyzed the systems-level mean-field model of basal ganglia nuclei to determine how it resonates under normal and pathological conditions.
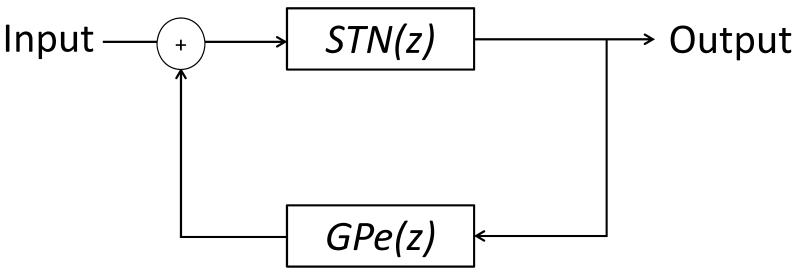
To analyze the emergence of oscillations in the closed-loop GPe-STN system, the transfer functions of each individual nucleus collected in open-loop were coupled together to create a systems-level model, illustrated in Figure 4. The closed-loop model describes the basal ganglia output given cortical inputs. The GPe-STN loop, QGPe,STN, can be determined as follows:
Where STN(z) is the transfer function describing the connection from STN to GPe, and GPe(z) is the transfer function describing the connection from GPe to STN. This model is easily extensible to incorporate more nuclei. Delays between the nuclei are incorporated.
Figure 4.
Box diagram of the closed-loop systems-level model. The Subthalamic nucleus (STN) receives input from the cortex and sends excitatory projections to the Globus Pallidus External (GPe). The GPe sends inhibitory projections back to STN. The transfer function of the closed-loop system describes the output of the system given the input.
QGPe,STN(z) can then be analyzed to determine the stability and characteristics of oscillatory activity. There are two complimentary ways to represent the behavior of the model. One is the pole-zero plot, and the other is the power spectrum. The roots of the denominator (the characteristic equation), 1 + GPe(z) × STN(z) = 0, describe the stability, dampening rate, and frequency of the oscillation emerging from the system. These roots can be plotted on a pole-zero plot to graphically represent the behavior of the system. The Bode plots can be generated by solving QGPe,STN(z) at particular frequencies and plotting the amplitudes of the resulting complex numbers to estimate the power spectrum of the system.
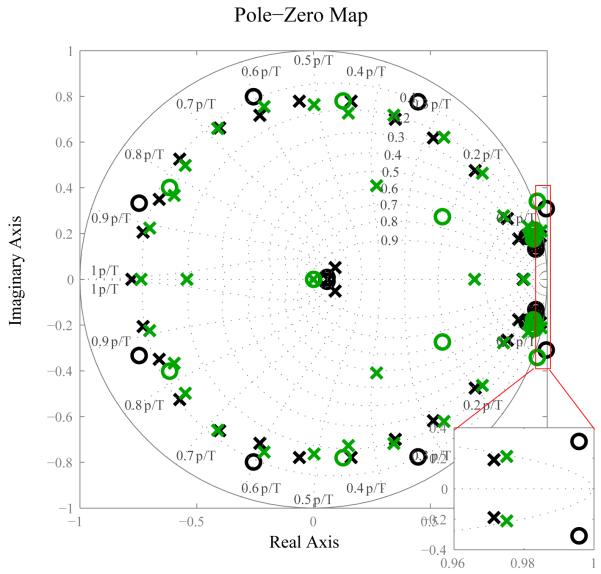
The pole-zero plot of QGPe,STN(z) plots the roots of the numerator, called the zeroes of the system, and of the denominator, called the poles. The roots can be complex, and the existence of an imaginary component indicates an oscillation in the system. The poles and zeroes of the z-transform can be plotted in the complex plane to create a pole-zero plot (Figure 5A). The poles of the PD state (green), , and healthy state (black), , are both plotted on the same graph for comparison. The two systems both contain complex poles, indicating that they oscillate. Both closed-loop systems are stable because all poles are within the unit circle, indicating that the system’s response to a bounded input decays with time. The poles closest to the edge of the unit circle have slower decays and therefore oscillate longer and dominate the behavior of the system. has poles closer to the edge of the circle than , therefore the model of the PD state has a stronger oscillation than that of the healthy state (Figure 5A inset). As poles move around the circle, away from the real axis, the frequencies of the oscillations increase. Poles of are further from the real axis than , indicating that the PD model will oscillate with a higher frequency.
Figure 5.
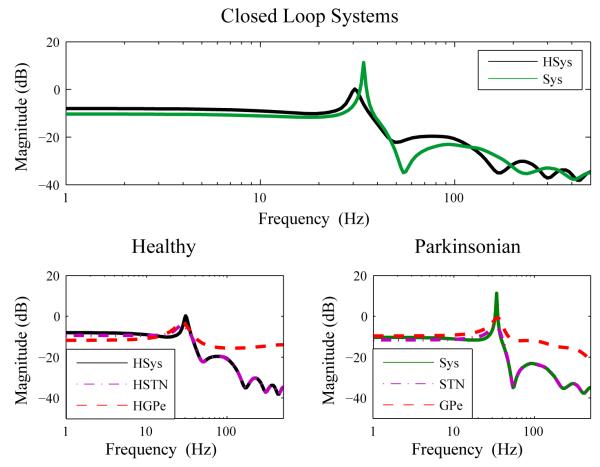
A) The PZ plot shows the poles and zeroes of the transfer function of a dynamical system. Poles are represented with X’s and zeroes are represented with O’s. The closed system in the PD state oscillates at a slightly shifted frequency and is less damped than the healthy state system. A pole-zero map showing the poles and zeros of the closed-loop GPe-STN system in the healthy (black) and PD (green) state. The x-axis is the real axis and the y-axis is the imaginary axis. All poles are within the unit circle, indicating they are stable. The poles closest to the edge of the unit circle characterize the oscillation seen in each state. The PD state will exhibit a less dampened oscillation, indicated by the pole being closer to the edge, at a slightly shifted frequency, indicated by the shift along the curved isodampening lines. B) The Parkinsonian closed loop STN-GPe system resonates better than the healthy system due STN and GPe resonating better with each other. Top: The PD system (green) resonates at 33 Hz while the healthy system resonates around 28 Hz at about half the magnitude. Bottom left: In the healthy state, STN (dotted purple) and GPe (dashed red) do not resonate as well with each other. Bottom right: STN (dotted purple) and GPe (dashed red) resonate better with each other in the PD state, resulting in better resonance in the closed system.
The power spectrum of QGPe,STN(z) is used to visualize how the system will amplify or dampen inputs (Figure 5B). The healthy system resonates at 30 Hz, while the parkinsonian system resonates at 34 Hz with a much higher magnitude. This oscillation frequency matches what we see in the Hahn and McIntyre model. Both the STN and GPe have some resonant properties in the healthy state and PD state, which can be seen in the impulse response curve in Figure 3 as well as the bode plot in Figure 5. However, the two nuclei resonate better with each other in the PD state than in the healthy state (Figure 5B), resulting in an oscillation of much higher magnitude in the closed-loop system.
2.3. Comparing Outputs from the Mean-Field Model and Hahn and McIntyre Model
In order to validate our simplified mean-field model, we compared the outputs to that of the full network Hahn and McIntyre model. The simplified model should produce outputs similar to the Hahn and McIntyre model as well as make predictions about how the full network model will behave under altered conditions.
2.3.1. Comparing Power Spectral Features
To model the actual time response of the GPe-STN loop, we ran simulations looking at the output of and in response to simulated cortical input. Cortical input was simulated using a pulse train generated by a double stochastic process, where the firing rate is modulated by an oscillation with a mean of 16 Hz, the mean frequency was varied using an Ornstein-Uhlenbeck process with a standard deviation of 1Hz (Figure 6 top). This cortical input was applied to the mean-field models and was similar to the cortical input used in the Hahn and McIntyre model. The time series of the output of the STN shows a peak at 34 Hz in the PD state, which is not present in the healthy state (Figure 6 bottom). The power spectrum from our simple closed-loop transfer function of the GPe-STN system was able to reproduce all the important spectral features of the full Hahn and McIntyre model (compare Figure 2 to Figure 6).
Figure 6.
Simulated cortical input used to drive the systems-level GPe-STN mean-field model produces spectral features similar to that seen in the Hahn and McIntyre model. Top: Input to the GPe-STN closed-loop transfer function. An Ornstein-Uhlenbeck process with a mean of 16 Hz was used to simulate cortical input applied in the Hahn and McIntyre model. Bottom: Power spectrum of the healthy GPe-STN system (black) and PD closed-loop GPe-STN system (green).
2.3.2. Making Predictions Using the Mean-Field Model
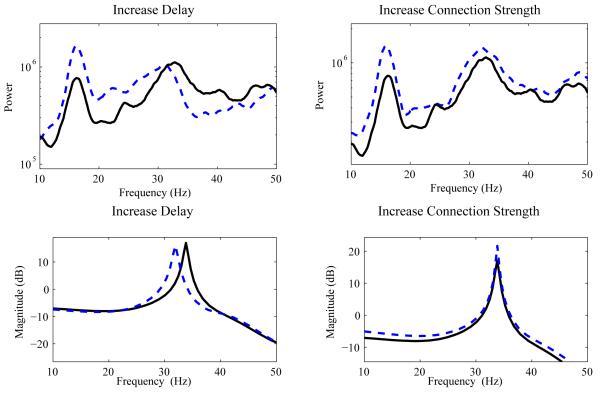
Next, we tested if our simplified model could predict changes in the behavior of the full Hahn and McIntyre model given a change in parameters. We first predicted how increasing the delay between GPe and STN from 4 to 7 msec would affect the amplitude and frequency of the oscillations. The simplified mean-field model of the GPe-STN loop, predicted a decrease in the resonant frequency from 34 Hz to 30 Hz with little effect on the magnitude. The same shift was seen in the Hahn and McIntyre model when the synaptic delay was increased proportionally (Figure 7, left column). Then, we predicted how changing the coupling strength between GPe and STN affected the behavior. In the mean-field model, , the gain of GPe was increased; this resulted in an increase in the magnitude of the resonant frequency, but had little effect on frequency. The same result was seen in the Hahn and McIntyre model when synaptic strength STN onto GPe was increased (Figure 7, right column).
Figure 7.
Changes in the closed-loop STN-GPe transfer function model predict changes seen in the Hahn & McIntyre model. Top left: By increasing the delay between GPe and STN from 4 ms to 6 ms, the peak oscillation shifts from 34 Hz to 30 Hz. Bottom left: By similarly changing the delays in the transfer function systems-level model, the resonance shifts in a similar way. Top right: Changing the connection strength between GPe and STN by increasing the maximum conductance increases the power in the oscillation. Bottom right: By increasing the connection strength in the transfer function model, the resonance has a higher magnitude.
2.4. Discussion
The systems-level mean-field model of the GPe-STN loop developed here differs from previously developed simplified models in that it incorporates various time delays between nuclei. Previous mean-field models of the basal ganglia have been used to determine conditions under which pathological beta oscillations emerge (Holgado et al., 2010; Pasillas-Lépine, 2013; van Albada et al., 2009; van Albada and Robinson, 2009). However, in order to determine how oscillations are generated in many of these models, delays between the nuclei are constrained to be equal. Changes in delays can affect the emergence of oscillations, making them an important aspect of the system. Delays have been incorporated into a mean-field model in the past to understand the effects various delays have on the stability of the system (Pasillas-Lépine, 2013). The discrete time mean-field model proposed here allows for an analytical and simpler analysis of the closed-loop behavior with various time delays between the nuclei. The power spectrum from our simple closed-loop mean-field model of the GPe-STN system displayed all important spectral features of the full Hahn and McIntyre model. Additionally, a discrete time approach enables us to predict the effects that changes in internuclear delays have on frequencies and amplitudes of the oscillation.
To verify that the simplified mean-field model accurately represented the full Hahn and McIntyre model, we tested whether changes to the mean-field model could predict outcomes from corresponding changes made in the Hahn and McIntyre model. To do this, changes in delays and gains were made to each model and the power spectra were compared. The mean-field model could accurately predict how changes in excitability and time delays altered the frequency and amplitude of the oscillations in the Hahn and McIntyre model. This indicates that simplified mean-field models may be an accurate representation of the realistic basal ganglia network and can be used to design optimal closed-loop therapies for suppressing oscillations.
In this paper, predictions of effective DBS frequencies were made using a single peak beta frequency. In patients, the peak beta frequency can be variable, which may impact the optimal frequency for disruption (Tsang et al., 2012). It should be tested if optimal DBS frequencies can be predicted across various peak beta frequencies. However, it is not clear if the Hahn and McIntyre model is an accurate model for parameters beyond which it was fit to the physiological data.
3. Stimulus Optimization
DBS efficacy depends on many factors including electrode placement (McClelland et al., 2005), patient physiology (Liang et al., 2006), electrode design (Butson and McIntyre, 2006), and post-operative parameter settings (Volkmann et al., 2002). High frequency DBS (>100 Hz) has been found to produce therapeutic benefit for motor signs of PD, while there is little efficacy at low frequencies (Alberts et al., 1969), highlighting the importance of frequency settings. The temporal pattern of stimulation also affects efficacy of DBS, with a periodic pattern being the most effective (Dorval et al., 2010; Dorval et al., 2008).
Currently, post-operative tuning of parameters depends on a clinician’s past experience along with trial-and-error (Volkmann et al., 2002). Patients can spend 18-41 hours in the clinic within the first year optimizing parameter settings (Hunka et al., 2005). There is a need for improved methods for determining optimal parameter settings. New DBS hardware has been developed that can simultaneously record and stimulate (Ryapolova-Webb et al., 2014), enabling new stimulus optimization approaches. The therapeutic benefit of a stimulation frequency for DBS may depend on the peak beta frequency of each individual patient, for example certain patients show a reduction in motor signs with 50 Hz stimulation, while others do not (Chen et al., 2007; Limousin et al., 1995; Moro et al., 2002; Rizzone et al., 2001; Timmermann et al., 2004; Tsang et al., 2012). This highlights the need for the tuning of DBS frequencies using patient-specific physiology. Our goal is to develop a method to optimize stimulus frequency parameters based on the patient’s physiology.
There are many hypotheses for how DBS works in PD: high frequency stimulation may alter the firing rates of neurons in target nuclei, leading to a decrease in the firing rate of pallidal neurons (McIntyre et al., 2004); or stimulation at a high enough rate may entrain pallidal neurons, disrupting information out of the network (Rubin and Terman, 2004). However, these hypotheses do not account for the fact that the pattern of stimulation, not just the rate, is important for effective treatment.
We have previously presented a hypothesis that DBS may work by chaotic desynchronization of a population oscillation (Wilson et al., 2011). It is well known in the physics literature that periodic forcing of an oscillating system can induce chaos (Glass and Mackey, 1988). The advantage of inducing a chaotic response in the basal ganglia is that neurons respond differently to the stimulus and these differences grow exponentially over time with stimulation until the system is no longer synchronized.
If DBS does suppress oscillations through chaotic desynchronization, then it may be possible to predict optimal stimulus frequencies to induce chaotic activity based on neuronal responses to stimulation. By measuring how a subthreshold stimulus changes the period of the population oscillation, represented by a phase response curve (PRC), stimulus frequencies that induce chaotic desynchronization can be predicted. PRCs have been used to characterize the response of the interspike interval of periodically firing single cells to stimulation (Lengyel et al., 2005; Netoff et al., 2005; Ota et al., 2009; Schultheiss et al., 2010; Stiefel et al., 2008; Torben-Nielsen et al., 2010). Here we develop a method for estimating PRCs from population activity, which is necessary for characterizing how a network oscillation responds to a stimulus pulse. From the measured PRC we predict which DBS frequencies are capable of suppressing an emergent pathological oscillation in the Hahn and McIntyre model.
3.1. Predicting Optimal Stimulus Frequencies from the PRC
In order to predict DBS frequencies capable of disrupting the beta oscillation seen in the Hahn and McIntyre model, we used DBS-like stimuli applied to the STN and measured the phase response curve of these oscillations. From the PRC, we predicted stimulus frequencies that will enhance and disrupt beta oscillations. Predictions were compared results from full simulations where we measured the effect of DBS frequency on the power of the pathological oscillation in the Hahn and McIntyre model.
The feedback loop from GPe-STN, found to be the origin of the pathological oscillation, can be thought of as a periodic oscillator. Specific frequencies of stimulation can entrain or desynchronize an oscillator (Glass and Mackey, 1988). These frequencies can be predicted using a phase response curve (PRC) of the oscillation to the stimulus. Previously, we have used PRCs to predict a single neuron’s response to periodic stimulation; however the oscillation in the Hahn and McIntyre model emerges from populations of neurons in different nuclei. Here we develop a method to estimate PRCs from population data.
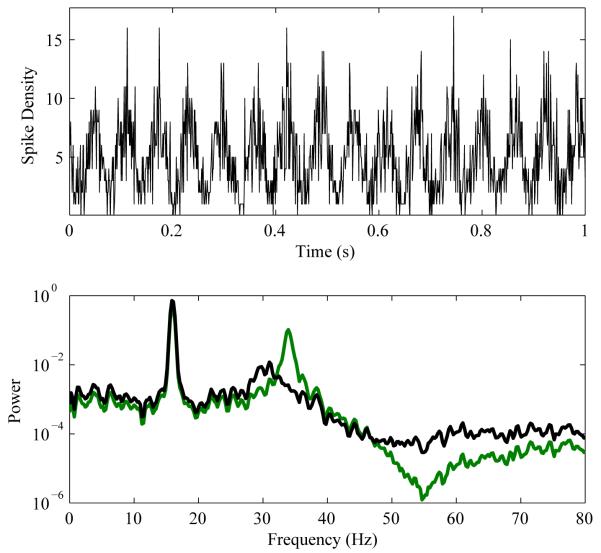
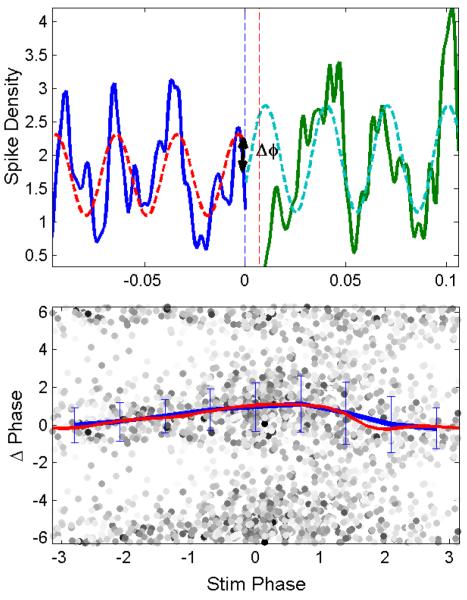
To estimate PRCs from the GPe population in the Hahn and McIntyre model a stimulus was applied to the STN at a low frequency so the system could recover before the application of the next stimulus. Spike times in a window before and after stimulation were Fourier transformed at 34 Hz, the frequency of the pathological oscillation. The Fourier coefficients were then used to estimate the instantaneous amplitude and phase of the population activity at the time of the stimulus. The change in phase caused by the stimulus was estimated as the difference between the phase prior to and after the stimulus. To estimate the PRC, a curve was fit to the phase change as a function of the stimulus phase. Each point was weighted by the amplitude of the oscillation prior to the stimulus in making the fit (Figure 8). Standard deviations of the phase advance were also estimated
Figure 8.
A phase response curve can be estimated from population local-field potential data. Top: Spike density preceding (solid blue) and following (green) a single stimulus, fit separately with a 34 Hz sine wave (dashed lines). Spikes evoked by the stimulus in a narrow window of time (between vertical dotted lines) are removed from analysis. Bottom: Phase change plotted against phase at stimulus onset with intensity of the dot indicating the amplitude of beta at the time of the stimulus.
3.1.1. Fourier Fit of Population PRC
A phase response curve (PRC) describes how the phase of an oscillator is changed as a result of a stimulus applied. Here we will describe how the phase, oscillation amplitude, and phase change are estimated from the neuronal spike times (considered a point process), and how a PRC is fit to the resulting data.
3.1.2. Estimating the Phase and Phase Change from Spike Time Data
There are many approaches that can be taken to estimate instantaneous amplitude and phase of the population oscillation at the time of stimulation from spike time data. One is to generate a PSTH of the spikes across the population and calculate the Fourier coefficient at the oscillation frequency, illustrated at the top of Figure 8. The Fourier coefficient, the Fourier transform at a selected frequency, ω = β, can be calculated from the spike density histogram as follows: . The Fourier coefficient Cβ is a complex number which can be represented as Cβ = Ae−jφ, where is the amplitude of the oscillation and is the phase. However, the Fourier coefficient can be calculated directly from the spike times without time binning, providing a more accurate estimation of the phase and amplitude.
A Fourier coefficient is fit to a window immediately prior to the stimulus i, and a window immediately after the stimulus , excluding any time containing stimulus artifacts. The amplitude and phase of the coefficients represent the amplitude and phase of the oscillation at the time of the stimulus.
3.1.3. Estimating the PRC from Population Activity
Given the phase of the oscillation estimated from the data preceding and following the stimulus, we can estimate the phase change .
The next step is to fit a function to the mean and standard deviation of the phase advance. This done by dividing the stimuli into phase bins and fitting a wrapped normal distribution to estimate the mean, μk, and standard deviation, σk, of the phase advance for each bin. The wrapped Gaussian is written as . To estimate the mean phase difference, we made a weighted average of the phases, weighting the changes proportionally to the amplitude of the oscillation at the time of the stimulus . The mean phase is the angle of the averaged vector . The standard deviation of the distribution of phase changes is inversely proportional to the length of the average phase change vector, where the * indicates the complex conjugate of . The variance of the distribution, corrected given the number of spikes seen at a particular phase bin Nbin can be calculated, . The estimated PRC is simply the mean phase, μk, change in phase bin k given the stimulation phase, PRC(φk) = μk.
To estimate the PRCs from the spike times from the Hahn and McIntyre model, all spikes in a window 94 msec (approximately three beta oscillations) before and after the stimulus were Fourier transformed at the oscillation frequency (34 Hz).
3.1.4. Transition Matrix and LE Calculation
From the PRC, we are able to determine whether the neuron will phase lock to a periodic stimulus by calculating the Lyapunov Exponent (LE). The LE of the system can be calculated given the PRC and the steady state distribution of phases given the stimulus frequency. If the LE is negative the oscillation will phase lock to the stimulation; if it is positive the stimulus will desynchronize the oscillation. To calculate the LE we need a transition matrix, which determines the expected distribution of spike times after a stimulus from the distribution at the time of the stimulus. From the transition matrix we can estimate the steady state distribution of neuronal phases at the time of stimuli.
A transition matrix can be generated to predict distribution of neuronal phases at the (ith+1) stimulus given the wrapped Gaussian distribution of phases at the ith stimulus.
Where is the probability distribution of the phases given a mean phase φμ and variance of the Gaussian distribution.
In order to fit the phase response curve to the distribution of phases, we use the mean of the phase advances, and are calculated as follows.
This curve fit to the mean representing the PRC is a simplification that ignores variability in the cell’s ISI (Wilson et al., 2011). In order to account for this, the variance must be calculated. The mean and variance of the phase after stimulation can be calculated from the phase response curve immediately before the stimulation. In Figure 8, the mean of the phase advances is the blue line, and the standard deviation is shown using error bars.
Where μpost represents the mean phase after stimulation and μpre, the mean phase before stimulation. The variance added at each stimulus is scaled by the average expected number of stimuli per cycle, ISI/StimISI, where ISI is the interspike-interval of the spike times, and StimISI is the interval between stimuli. Over many stimuli, the distributions will converge to a steady-state probability distribution independent of the starting distribution. The steady-state distribution is the eigenvector, λ(φ), corresponding to the largest eigenvalue of the transition matrix, (Ermentrout et al., 2011).
The Lyapunov exponent (LE) is a measure of the rate of divergence between two neurons firing at almost the same time in response to the stimulus. It is calculated as the average slope of the PRC, weighting each phase by the probability of neurons firing at that phase (Wilson et al., 2011). The LE can be calculated as:
Where PRC’(Φ) is the slope of the PRC. The PRC used in estimating the LE was measured by stimulating the STN at a frequency of 2 Hz to limit interactions between stimulus pulses.
3.1.5. Predictions
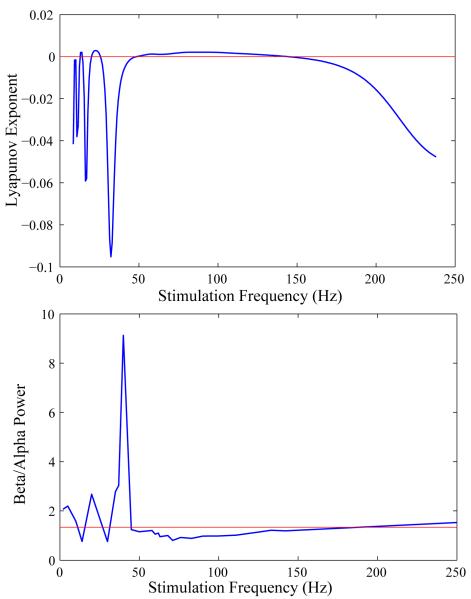
Using the PRC estimated from the population, we predicted stimulation frequencies that would entrain the population oscillation seen in the Hahn and McIntyre model and those that would suppress it. This was done by calculating the Lyapunov Exponent (LE) of the oscillation response to the periodic stimulation. The LE was calculated for a range of stimulus frequencies (Figure 9 top). When the LE is above zero, we predict that the population oscillation will be disrupted. The most positive LE was estimated to be around 85 Hz. We also predict that stimulation at frequencies close to the natural frequency of the oscillation will entrain and enhance the oscillation.
Figure 9.
Predicting DBS frequencies to disrupt population oscillations using the Lyapunov exponent. Top: Lyapunov exponent as a function of DBS frequency determined from the phase-response curve. Values above the red line (above zero) are predicted to disrupt oscillations. Bottom: Ratio of beta:alpha power as a function of DBS frequency. Beta power: 32-36 Hz. Alpha power: 12-16 Hz. Red line is beta:alpha power with DBS off.
Simulations were then run in the Hahn and McIntyre model applying DBS at various frequencies. At each frequency the power of the beta oscillation (32-38 Hz) was estimated as a ratio to the power in the alpha (12-16 Hz) frequency band. Because beta oscillations were strongest in the non-bursting phase of the spiking, the spikes from the bursting phase of neurons were removed for this analysis. Stimulation suppressed the beta oscillation when the ratio of beta/alpha power fell below that seen in the DBS off state. While 136 Hz stimulation suppressed the beta oscillation, the maximum suppression occurred at 75 Hz. The most effective stimulation frequency was close to that predicted using the LE measured from the PRC (85 Hz).
3.2. Discussion: Suppression of Pathological Oscillations
The pathological oscillation seen in the Hahn and McIntyre model emerged in the non-bursting firing and was suppressed using 136 Hz stimulation to the STN. We propose that the phase response curve (PRC) of the beta oscillation’s response to subthreshold DBS-like pulses is a physiological measure that can be used to predict optimal stimulus frequencies.
In this paper, we developed a novel method for determining the phase response curve from population data. Previously, PRCs have been applied to the spike timing of individual neurons (Lengyel et al., 2005; Netoff et al., 2005; Ota et al., 2009; Schultheiss et al., 2010; Stiefel et al., 2008; Torben-Nielsen et al., 2010). Here we developed methods for the estimation of PRCs from local field potentials, enabling the application to human data. To our knowledge, this is the first PRC method developed for application to neuronal populations.
Using the population PRC, we were able to predict DBS frequencies capable of suppressing the pathological beta oscillation seen in the Hahn and McIntyre model. Predictions of frequencies capable of suppressing the beta oscillation were compared to reductions in beta power measured in the Hahn and McIntyre model during DBS over a range of frequencies. We found that while 136 Hz DBS, the value used in the original paper and clinically, suppressed the beta oscillation, it was not the optimal frequency. The optimal stimulus frequency predicted by the PRC was close to that which maximally suppressed the beta oscillation in the model.
Predictions made using the PRC were close to, but not exactly, commensurate with the findings in the full Hahn and McIntyre model. This may be because our PRC did not account for interactions between stimulus pulses, and is therefore a first approximation. There are ways to improve predictions by accounting for these higher order effects in the measurement of the PRC (Cui et al., 2009). However, we have yet to incorporate them into the estimate of the Lyapunov exponent.
4. Discussion
In this paper we were able to determine where and why a pathological oscillation emerged in a computational model of the basal ganglia as well as accurately predict stimulation frequencies to suppress this oscillation with DBS. The discrete-time mean-field models may be fit using LFP data collected from non-human primates to describe the origins of pathological beta oscillations, which remain controversial. Understanding how these pathological oscillations are generated may help in the design of future therapies and provide insight into why strong beta oscillations are seen in some subjects but not others with the same pathology. The PRC-based parameter optimization may be used to reduce time and resources spent in the clinic as well as improve efficacy of the therapy.
4.1. Emergence of Pathological Oscillation
In this paper a mean-field model, consisting of discrete time models and their Z-transforms, was used to explain the emergence of a pathological oscillation in the Hahn and McIntyre model. Our approach involves fitting transfer functions to impulse responses in the STN and GPe in open-loop, and connecting them with delays to understand the closed-loop GPe-STN system. The analysis of the closed-loop system indicated that the resonant frequencies of GPe and STN were better matched in the PD condition, enabling the population to oscillate stronger than in the healthy condition. Cortical drive was still needed for the emergence of the oscillation in the full Hahn and McIntyre model, however did not need to be oscillatory. Simplified mean-field models fit to experimental LFP recordings in response to stimulation, represented by the output of the Hahn and McIntyre model in this paper, could be used to help answer the debate about how pathological oscillations emerge in PD. The models can disambiguate between oscillations that emerge from the cortex and are patterned onto the basal ganglia nuclei from oscillations that arise within the basal ganglia network. The mean-field model presented here only accounted for the GPe-STN loop; however, other nuclei can be added to make a more complete model if necessary. By fitting models to patient data, they may help explain differences seen across patients, such as why some patients have strong beta oscillations and others do not.
Beta oscillations are variable across patients. The method developed in this paper could help determine why some patients exhibit beta oscillations and others do not, or why the peak beta frequency is different across patients (Kühn et al., 2009; Tsang et al., 2012). It has been found that individual peak beta power frequency matters when determining optimal DBS frequencies to suppress motor signs (Tsang et al., 2012).
4.2. Suppression of Pathological Oscillation
The use of the PRC has the potential to aid clinicians in finding an optimal stimulus frequency and amplitude setting for each particular patient. PRC-based parameter optimization could help identify stimulus parameters outside of the standard parameter regime that may be more effective and/or robust. With the development of DBS devices which can simultaneously record and stimulate, the method could be used to optimize DBS frequencies for each individual patient based on his or her measured PRC. PRCs could be measured by applying a subthreshold stimulus pulse at 2 Hz for a couple minutes and then fitting a function to the resulting data. The fit PRC would then be used to select a DBS frequency in the neighborhood of the optimal solution. This stimulus frequency could then be applied and the PRC reassessed. By iteratively predicting and testing new stimulus frequencies, an optimal stimulus may be designed within a few minutes. This systematic approach could replace the current trial-and-error tuning process and aid clinicians in finding successful parameter windows. Automating the tuning process could reduce the time patients spend in the clinic and potentially improve the efficacy and robustness of the treatment.
Previous optimization methods have been proposed to improve post-operative programming of DBS parameters. Some involved using kinematic data collected from wearable sensing devices (Mera et al., 2011), optimizing stimulus waveforms using genetic algorithms in computational models (Feng et al., 2007), and using a model reference control to restore the power spectrum of the pathological condition to that measured in the healthy condition through DBS (Santaniello et al., 2011). Our work differs from these efforts in that it uses responses to subthreshold stimulation to provide an initial prediction about frequency settings. Underlying this method is the explicit assumption that DBS works by inducing chaos in the basal ganglia network, thereby disrupting a pathological oscillation. If this approach is successful in optimizing DBS therapy, it will provide insight into the mechanisms of the origins of the oscillations and the effects of DBS.
The approach presented in this paper has several advantages over current methods for estimating optimal stimulus frequencies, even as a first approximation. The first is that it provides a formal process for estimating optimal parameter settings, which may help standardize therapies and reduce tuning time. The method could also be automated and used to update the patient’s stimulation parameters over time, if the patient’s response to the stimulus changes. Second, a clinician generally changes parameters and monitors a behavioral output, such as tremor. When the tremor disappears, the tuning process stops. However, the final settings may only be at the edge of a window of effective parameters. After the behavioral biomarker is suppressed, it is difficult to further improve the therapy. Our PRC-based parameter optimization approach may find parameters closer to the center of this effective window, and therefore may produce more reliable and robust patient outcomes.
Whether the suppression of pathological beta oscillations produces the desired reduction in motor signs of PD remains to be determined. The correlation between beta oscillations and motor signs of PD is controversial (Brown, 2006; Dorval and Grill, 2014; Eusebio and Brown, 2007; Hammond et al., 2007; Kuhn et al., 2006), particularly in the non-human primate model (Devergnas et al., 2014). In order to predict therapeutic DBS frequencies, the correct biomarker must be used. If beta oscillations are determined to be a poor biomarker of disease pathology, the PRC-based parameter optimization method can be applied to other pathological oscillatory activity in PD. Additionally, this method can be used to identify stimulus parameters for a number of other diseases such as epilepsy, schizophrenia, or sleep disorders that involve pathological oscillations and are being considered for DBS therapy.
This work provides a method for understanding the emergence of beta oscillations in parkinsonian patients, which may help explain variance seen among patients, as well as for developing a closed-loop approach to tuning DBS frequency. A closed-loop approach to parameter tuning may help conserve energy, account for changes in motor sign severity, and improve therapeutic outcome. With the development of electrodes that can simultaneously stimulate and record (Ryapolova-Webb et al., 2014), it may be possible to monitor the power beta frequency power and determine the optimal stimulus frequency based on PRCs.
4.3. Future Directions
To understand where pathological oscillations are coming from in vivo, simplified discrete time mean-field models could be fit directly to electrophysiology data acquired from humans or non-human primates. Open-loop experiments that would be necessary to replicate the open-loop paradigm used in this paper have been done with pharmacological block in non-human primates (Tachibana et al., 2008). However, open-loop measurements cannot at present be done ethically in humans. Potentially, multi-site stimulation and recordings may enable us to develop accurate models under closed-loop conditions in humans. Chronic LFP recordings from the basal ganglia of PD patients should soon be available from studies using the Activa PC+S DBS neurostimulators (Ryapolova-Webb et al., 2014).
In this paper, we attempted to optimize temporally regular stimuli. However, various other stimulus paradigms have been proposed (Adamchic et al., 2014; Birdno et al., 2008; McConnell et al., 2012; Tass, 2003). In the future, we will test temporally irregular stimulus trains and closed-loop stimulation algorithms to stimulate at particular phases of the beta oscillation to determine their efficacy over fixed interval periodic stimulation currently used in therapy.
4.4. Conclusion
This work provides a method for understanding the emergence of beta oscillations in parkinsonian patients, which may help explain variance seen among patients, as well as for developing a closed-loop approach to tuning DBS frequency. With the development of electrodes that can simultaneously stimulate and record (Ryapolova-Webb et al., 2014), it may be possible to monitor the power beta frequency power and determine the optimal stimulus frequency based on PRCs.
Acknowledgements
Supported by MnDrive Fellowship, National Science Foundation IGERT DGE-1069 104, NSF Collaborative research grant 1264432, Medtronic, Netoff CAREER 0954797, Neuroscience R21 institutional training grant 2T32GM008471.
Contributor Information
ABBEY B. HOLT, Graduate Program in Neuroscience, University of Minnesota, Minneapolis, MN 55455, USA, [email protected]
THEODEN I. NETOFF, Department of Biomedical Engineering, University of Minnesota, Minneapolis, MN 55455, USA.
References
- Adamchic I, Hauptmann C, Barnikol UB, Pawelczyk N, Popovych O, Barnikol TT, Silchenko A, Volkmann J, Deuschl G, Meissner WG, Maarouf M, Sturm V, Freund HJ, Tass PA. Coordinated reset neuromodulation for Parkinson’s disease: Proof-of-concept study. Mov Disord. 2014 doi: 10.1002/mds.25923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberts WW, Wright EW, Jr., Feinstein B. Cortical potentials and Parkinsonian tremor. Nature. 1969;221:670–672. doi: 10.1038/221670a0. [DOI] [PubMed] [Google Scholar]
- Albin RL, Young AB, Penney JB. The functional anatomy of basal ganglia disorders. Trends Neurosci. 1989;12:366–75. doi: 10.1016/0166-2236(89)90074-x. [DOI] [PubMed] [Google Scholar]
- Alexander GE, DeLong MR, Strick PL. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu Rev Neurosci. 1986;9:357–81. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- Bernheimer H, Birkmeyer W, Hornykiewicz O, Jellinger K, Seitelberger F. Brain dopamine and the syndromes of Parkinson and Huntington. J. Neurol Sci. 1973;20:415–445. doi: 10.1016/0022-510x(73)90175-5. [DOI] [PubMed] [Google Scholar]
- Bevan MD, Magill PJ, Terman D, Bolam JP, Wilson CJ. Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends in neurosciences. 2002;25:525–531. doi: 10.1016/s0166-2236(02)02235-x. [DOI] [PubMed] [Google Scholar]
- Bevan MD, Wilson CJ. Mechanisms underlying spontaneous oscillation and rhythmic firing in rat subthalamic neurons. The Journal of neuroscience: the official journal of the Society for Neuroscience. 1999;19:7617–7628. doi: 10.1523/JNEUROSCI.19-17-07617.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhidayasiri R, Truong DD. Motor complications in Parkinson disease: clinical manifestations and management. Journal of the neurological sciences. 2008;266:204–215. doi: 10.1016/j.jns.2007.08.028. [DOI] [PubMed] [Google Scholar]
- Birdno MJ, Kuncel AM, Dorval AD, Turner DA, Grill WM. Tremor varies as a function of the temporal regularity of deep brain stimulation. Neuroreport. 2008;19:599–602. doi: 10.1097/WNR.0b013e3282f9e45e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bronte-Stewart H, Barberini C, Koop MM, Hill BC, Henderson JM, Wingeier B. The STN beta-band profile in Parkinson’s disease is stationary and shows prolonged attenuation after deep brain stimulation. Experimental neurology. 2009;215:20–28. doi: 10.1016/j.expneurol.2008.09.008. [DOI] [PubMed] [Google Scholar]
- Brown P. Bad oscillations in Parkinson’s disease. J Neural Transm Suppl. 2006:27–30. doi: 10.1007/978-3-211-45295-0_6. [DOI] [PubMed] [Google Scholar]
- Brown P, Williams D. Basal ganglia local field potential activity: character and functional significance in the human. Clinical neurophysiology: official journal of the International Federation of Clinical Neurophysiology. 2005;116:2510–2519. doi: 10.1016/j.clinph.2005.05.009. [DOI] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Role of electrode design on the volume of tissue activated during deep brain stimulation. Journal of neural engineering. 2006;3:1–8. doi: 10.1088/1741-2560/3/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CC, Litvak V, Gilbertson T, Kühn A, Lu CS, Lee ST, Tsai CH, Tisch S, Limousin P, Hariz M, Brown P. Excessive synchronization of basal ganglia neurons at 20 Hz slows movement in Parkinson’s disease. Exp Neurol. 2007;205:214–21. doi: 10.1016/j.expneurol.2007.01.027. [DOI] [PubMed] [Google Scholar]
- Courtemanche R, Fujii N, Graybiel AM. Synchronous, focally modulated beta-band oscillations characterize local field potential activity in the striatum of awake behaving monkeys. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2003;23:11741–11752. doi: 10.1523/JNEUROSCI.23-37-11741.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui J, Canavier CC, Butera RJ. Functional phase response curves: a method for understanding synchronization of adapting neurons. J Neurophysiol. 2009;102:387–98. doi: 10.1152/jn.00037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dejean C, Hyland B, Arbuthnott G. Cortical effects of subthalamic stimulation correlate with behavioral recovery from dopamine antagonist induced akinesia. Cereb Cortex. 2009;19:1055–63. doi: 10.1093/cercor/bhn149. [DOI] [PubMed] [Google Scholar]
- DeLong MR, Alexander GE, Miller WC, Crutcher MD. Anatomical and functional aspects of basal ganglia-thalamocortical circuits. In: Ironside JW, Mindham RHS, Smith RJ, Spokes EGS, Winlow W, editors. Function and dysfunction in the basal ganglia. Rergamon Press; OxfordNew YorkSeoulTokyo: 1992. pp. 3–32. [Google Scholar]
- Devergnas A, Pittard D, Bliwise D, Wichmann T. Relationship between oscillatory activity in the cortico-basal ganglia network and parkinsonism in MPTP-treated monkeys. Neurobiol Dis. 2014;68C:156–166. doi: 10.1016/j.nbd.2014.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorval AD, Grill WM. Deep Brain Stimulation of the Subthalamic Nucleus Reestablishes Neuronal Information Transmission in the 6-OHDA Rat Model of Parkinsonism. J Neurophysiol. 2014 doi: 10.1152/jn.00713.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorval AD, Kuncel AM, Birdno MJ, Turner DA, Grill WM. Deep brain stimulation alleviates parkinsonian bradykinesia by regularizing pallidal activity. Journal of neurophysiology. 2010;104:911–921. doi: 10.1152/jn.00103.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorval AD, Russo GS, Hashimoto T, Xu W, Grill WM, Vitek JL. Deep brain stimulation reduces neuronal entropy in the MPTP-primate model of Parkinson’s disease. Journal of neurophysiology. 2008;100:2807–2818. doi: 10.1152/jn.90763.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB, Beverlin B, 2nd, Troyer T, Netoff TI. The variance of phase-resetting curves. Journal of computational neuroscience. 2011;31:185–197. doi: 10.1007/s10827-010-0305-9. [DOI] [PubMed] [Google Scholar]
- Eusebio A, Brown P. Oscillatory activity in the basal ganglia. Parkinsonism Relat Disord. 2007;13(Suppl 3):S434–6. doi: 10.1016/S1353-8020(08)70044-0. [DOI] [PubMed] [Google Scholar]
- Feng XJ, Greenwald B, Rabitz H, Shea-Brown E, Kosut R. Toward closed-loop optimization of deep brain stimulation for Parkinson’s disease: concepts and lessons from a computational model. Journal of neural engineering. 2007;4:L14–21. doi: 10.1088/1741-2560/4/2/L03. [DOI] [PubMed] [Google Scholar]
- Gillies A, Willshaw D. Neuroinformatics and modeling of the basal ganglia: bridging pharmacology and physiology. Expert review of medical devices. 2007;4:663–672. doi: 10.1586/17434440.4.5.663. [DOI] [PubMed] [Google Scholar]
- Glass L, Mackey MC. From clocks to chaos: the rhythms of life. Princeton University Press; Princeton, N.J.: 1988. p. 248. [Google Scholar]
- Goldberg JA, Bourad T, Bergman H. Microrecording in the Primate MPTP Model. 2004. p. 46. [Google Scholar]
- Gradinaru V, Mogri M, Thompson KR, Henderson JM, Deisseroth K. Optical deconstruction of parkinsonian neural circuitry. Science (New York, N.Y.) 2009;324:354–359. doi: 10.1126/science.1167093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green AL, Aziz TZ. Steering technology for deep brain stimulation. Brain. 2014 doi: 10.1093/brain/awu126. [DOI] [PubMed] [Google Scholar]
- Hahn PJ, McIntyre CC. Modeling shifts in the rate and pattern of subthalamopallidal network activity during deep brain stimulation. Journal of computational neuroscience. 2010;28:425–441. doi: 10.1007/s10827-010-0225-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond C, Bergman H, Brown P. Pathological synchronization in Parkinson’s disease: networks, models and treatments. Trends in neurosciences. 2007;30:357–364. doi: 10.1016/j.tins.2007.05.004. [DOI] [PubMed] [Google Scholar]
- Hashimoto T, Elder CM, Okun MS, Patrick SK, Vitek JL. Stimulation of the subthalamic nucleus changes the firing pattern of pallidal neurons. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2003;23:1916–1923. doi: 10.1523/JNEUROSCI.23-05-01916.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. NEURON: a tool for neuroscientists. Neuroscientist. 2001;7:123–35. doi: 10.1177/107385840100700207. [DOI] [PubMed] [Google Scholar]
- Holgado AJ, Terry JR, Bogacz R. Conditions for the generation of beta oscillations in the subthalamic nucleus-globus pallidus network. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2010;30:12340–12352. doi: 10.1523/JNEUROSCI.0817-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunka K, Suchowersky O, Wood S, Derwent L, Kiss ZH. Nursing time to program and assess deep brain stimulators in movement disorder patients. The Journal of neuroscience nursing: journal of the American Association of Neuroscience Nurses. 2005;37:204–210. doi: 10.1097/01376517-200508000-00006. [DOI] [PubMed] [Google Scholar]
- Jenner P. The contribution of the MPTP-treated primate model to the development of new treatment strategies for Parkinson’s disease. Parkinsonism Relat Disord. 2003;9:131–7. doi: 10.1016/s1353-8020(02)00115-3. [DOI] [PubMed] [Google Scholar]
- Jenner P. Functional models of Parkinson’s disease: a valuable tool in the development of novel therapies. Ann Neurol. 2008;64(Suppl 2):S16–29. doi: 10.1002/ana.21489. [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Kempf F, Brucke C, Gaynor Doyle L, Martinez-Torres I, Pogosyan A, Trottenberg T, Kupsch A, Schneider GH, Hariz MI, Vandenberghe W, Nuttin B, Brown P. High-frequency stimulation of the subthalamic nucleus suppresses oscillatory beta activity in patients with Parkinson’s disease in parallel with improvement in motor performance. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2008;28:6165–6173. doi: 10.1523/JNEUROSCI.0282-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn AA, Kupsch A, Schneider GH, Brown P. Reduction in subthalamic 8-35 Hz oscillatory activity correlates with clinical improvement in Parkinson’s disease. Eur J Neurosci. 2006;23:1956–60. doi: 10.1111/j.1460-9568.2006.04717.x. [DOI] [PubMed] [Google Scholar]
- Kuhn AA, Trottenberg T, Kivi A, Kupsch A, Schneider GH, Brown P. The relationship between local field potential and neuronal discharge in the subthalamic nucleus of patients with Parkinson’s disease. Exp Neurol. 2005;194:212–20. doi: 10.1016/j.expneurol.2005.02.010. [DOI] [PubMed] [Google Scholar]
- Kühn AA, Tsui A, Aziz T, Ray N, Brücke C, Kupsch A, Schneider GH, Brown P. Pathological synchronisation in the subthalamic nucleus of patients with Parkinson’s disease relates to both bradykinesia and rigidity. Exp Neurol. 2009;215:380–7. doi: 10.1016/j.expneurol.2008.11.008. [DOI] [PubMed] [Google Scholar]
- Langston JW, Ballard P, Tetrud JW, Irwin I. Chronic Parkinsonism in humans due to a product of meperidine-analog synthesis. Science. 1983;219:979–80. doi: 10.1126/science.6823561. [DOI] [PubMed] [Google Scholar]
- Leblois A, Boraud T, Meissner W, Bergman H, Hansel D. Competition between feedback loops underlies normal and pathological dynamics in the basal ganglia. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2006;26:3567–3583. doi: 10.1523/JNEUROSCI.5050-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lengyel M, Kwag J, Paulsen O, Dayan P. Matching storage and recall: hippocampal spike timing-dependent plasticity and phase response curves. Nat Neurosci. 2005;8:1677–83. doi: 10.1038/nn1561. [DOI] [PubMed] [Google Scholar]
- Liang GS, Chou KL, Baltuch GH, Jaggi JL, Loveland-Jones C, Leng L, Maccarone H, Hurtig HI, Colcher A, Stern MB, Kleiner-Fisman G, Simuni T, Siderowf AD. Long-term outcomes of bilateral subthalamic nucleus stimulation in patients with advanced Parkinson’s disease. Stereotactic and functional neurosurgery. 2006;84:221–227. doi: 10.1159/000096495. [DOI] [PubMed] [Google Scholar]
- Limousin P, Pollak P, Benazzouz A, Hoffmann D, Le Bas JF, Broussolle E, Perret JE, Benabid AL. Effect of parkinsonian signs and symptoms of bilateral subthalamic nucleus stimulation. Lancet. 1995;345:91–5. doi: 10.1016/s0140-6736(95)90062-4. [DOI] [PubMed] [Google Scholar]
- Mallet N, Pogosyan A, Marton LF, Bolam JP, Brown P, Magill PJ. Parkinsonian beta oscillations in the external globus pallidus and their relationship with subthalamic nucleus activity. J Neurosci. 2008;28:14245–58. doi: 10.1523/JNEUROSCI.4199-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marreiros AC, Cagnan H, Moran RJ, Friston KJ, Brown P. Basal ganglia-cortical interactions in Parkinsonian patients. Neuroimage. 2012;66c:301–310. doi: 10.1016/j.neuroimage.2012.10.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy MM, Moore-Kochlacs C, Gu X, Boyden ES, Han X, Kopell N. Striatal origin of the pathologic beta oscillations in Parkinson’s disease. Proc Natl Acad Sci U S A. 2011;108:11620–5. doi: 10.1073/pnas.1107748108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland S, 3rd, Ford B, Senatus PB, Winfield LM, Du YE, Pullman SL, Yu Q, Frucht SJ, McKhann GM, 2nd, Goodman RR. Subthalamic stimulation for Parkinson disease: determination of electrode location necessary for clinical efficacy. Neurosurgical focus. 2005;19:E12. [PubMed] [Google Scholar]
- McConnell GC, So RQ, Hilliard JD, Lopomo P, Grill WM. Effective deep brain stimulation suppresses low-frequency network oscillations in the basal ganglia by regularizing neural firing patterns. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2012;32:15657–15668. doi: 10.1523/JNEUROSCI.2824-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. Journal of neurophysiology. 2004;91:1457–1469. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- Meissner W, Leblois A, Hansel D, Bioulac B, Gross CE, Benazzouz A, Boraud T. Subthalamic high frequency stimulation resets subthalamic firing and reduces abnormal oscillations. Brain: a journal of neurology. 2005;128:2372–2382. doi: 10.1093/brain/awh616. [DOI] [PubMed] [Google Scholar]
- Mera T, Vitek JL, Alberts JL, Giuffrida JP. Kinematic optimization of deep brain stimulation across multiple motor symptoms in Parkinson’s disease. Journal of neuroscience methods. 2011;198:280–286. doi: 10.1016/j.jneumeth.2011.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran RJ, Mallet N, Litvak V, Dolan RJ, Magill PJ, Friston KJ, Brown P. Alterations in brain connectivity underlying beta oscillations in Parkinsonism. PLoS Comput Biol. 2011;7:e1002124. doi: 10.1371/journal.pcbi.1002124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moro E, Esselink RJ, Xie J, Hommel M, Benabid AL, Pollak P. The impact on Parkinson’s disease of electrical parameter settings in STN stimulation. Neurology. 2002;59:706–13. doi: 10.1212/wnl.59.5.706. [DOI] [PubMed] [Google Scholar]
- Netoff TI, Banks MI, Dorval AD, Acker CD, Haas JS, Kopell N, White JA. Synchronization in hybrid neuronal networks of the hippocampal formation. Journal of neurophysiology. 2005;93:1197–1208. doi: 10.1152/jn.00982.2004. [DOI] [PubMed] [Google Scholar]
- Nevado-Holgado AJ, Mallet N, Magill PJ, Bogacz R. Effective connectivity of the subthalamic nucleus-globus pallidus network during Parkinsonian oscillations. J Physiol. 2014;592:1429–55. doi: 10.1113/jphysiol.2013.259721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oppenheim AV, Willsky AS, Nawab SH. Signals & systems. 2nd ed. Prentice-Hall, Inc.; 1996. [Google Scholar]
- Ota K, Omori T, Aonishi T. MAP estimation algorithm for phase response curves based on analysis of the observation process. J Comput Neurosci. 2009;26:185–202. doi: 10.1007/s10827-008-0104-8. [DOI] [PubMed] [Google Scholar]
- Pasillas-Lépine W. Delay-induced oscillations in Wilson and Cowan’s model: an analysis of the subthalamo-pallidal feedback loop in healthy and parkinsonian subjects. Biol Cybern. 2013;107:289–308. doi: 10.1007/s00422-013-0549-3. [DOI] [PubMed] [Google Scholar]
- Plenz D, Kital ST. A basal ganglia pacemaker formed by the subthalamic nucleus and external globus pallidus. Nature. 1999;400:677–682. doi: 10.1038/23281. [DOI] [PubMed] [Google Scholar]
- Rizzone M, Lanotte M, Bergamasco B, Tavella A, Torre E, Faccani G, Melcarne A, Lopiano L. Deep brain stimulation of the subthalamic nucleus in Parkinson’s disease: effects of variation in stimulation parameters. J Neurol Neurosurg Psychiatry. 2001;71:215–9. doi: 10.1136/jnnp.71.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin JE, Terman D. High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model. Journal of computational neuroscience. 2004;16:211–235. doi: 10.1023/B:JCNS.0000025686.47117.67. [DOI] [PubMed] [Google Scholar]
- Ryapolova-Webb E, Afshar P, Stanslaski S, Denison T, de Hemptinne C, Bankiewicz K, Starr PA. Chronic cortical and electromyographic recordings from a fully implantable device: preclinical experience in a nonhuman primate. J Neural Eng. 2014;11:016009. doi: 10.1088/1741-2560/11/1/016009. [DOI] [PubMed] [Google Scholar]
- Santaniello S, Fiengo G, Glielmo L, Grill WM. Closed-loop control of deep brain stimulation: a simulation study. IEEE transactions on neural systems and rehabilitation engineering: a publication of the IEEE Engineering in Medicine and Biology Society. 2011;19:15–24. doi: 10.1109/TNSRE.2010.2081377. [DOI] [PubMed] [Google Scholar]
- Schultheiss NW, Edgerton JR, Jaeger D. Phase response curve analysis of a full morphological globus pallidus neuron model reveals distinct perisomatic and dendritic modes of synaptic integration. J Neurosci. 2010;30:2767–82. doi: 10.1523/JNEUROSCI.3959-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharott A, Magill PJ, Harnack D, Kupsch A, Meissner W, Brown P. Dopamine depletion increases the power and coherence of beta-oscillations in the cerebral cortex and subthalamic nucleus of the awake rat. Eur J Neurosci. 2005;21:1413–22. doi: 10.1111/j.1460-9568.2005.03973.x. [DOI] [PubMed] [Google Scholar]
- Stiefel KM, Gutkin BS, Sejnowski TJ. Cholinergic neuromodulation changes phase response curve shape and type in cortical pyramidal neurons. PLoS One. 2008;3:e3947. doi: 10.1371/journal.pone.0003947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tachibana Y, Kita H, Chiken S, Takada M, Nambu A. Motor cortical control of internal pallidal activity through glutamatergic and GABAergic inputs in awake monkeys. The European journal of neuroscience. 2008;27:238–253. doi: 10.1111/j.1460-9568.2007.05990.x. [DOI] [PubMed] [Google Scholar]
- Tass PA. A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biol Cybern. 2003;89:81–8. doi: 10.1007/s00422-003-0425-7. [DOI] [PubMed] [Google Scholar]
- Terman D, Rubin JE, Yew AC, Wilson CJ. Activity patterns in a model for the subthalamopallidal network of the basal ganglia. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2002;22:2963–2976. doi: 10.1523/JNEUROSCI.22-07-02963.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmermann L, Wojtecki L, Gross J, Lehrke R, Voges J, Maarouf M, Treuer H, Sturm V, Schnitzler A. Ten-Hertz stimulation of subthalamic nucleus deteriorates motor symptoms in Parkinson’s disease. Mov Disord. 2004;19:1328–33. doi: 10.1002/mds.20198. [DOI] [PubMed] [Google Scholar]
- Torben-Nielsen B, Uusisaari M, Stiefel KM. A comparison of methods to determine neuronal phase-response curves. Front Neuroinform. 2010;4:6. doi: 10.3389/fninf.2010.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsang EW, Hamani C, Moro E, Mazzella F, Saha U, Lozano AM, Hodaie M, Chuang R, Steeves T, Lim SY, Neagu B, Chen R. Subthalamic deep brain stimulation at individualized frequencies for Parkinson disease. Neurology. 2012;78:1930–8. doi: 10.1212/WNL.0b013e318259e183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Albada SJ, Gray RT, Drysdale PM, Robinson PA. Mean-field modeling of the basal ganglia-thalamocortical system. II Dynamics of parkinsonian oscillations. Journal of theoretical biology. 2009;257:664–688. doi: 10.1016/j.jtbi.2008.12.013. [DOI] [PubMed] [Google Scholar]
- van Albada SJ, Robinson PA. Mean-field modeling of the basal ganglia-thalamocortical system. I Firing rates in healthy and parkinsonian states. Journal of theoretical biology. 2009;257:642–663. doi: 10.1016/j.jtbi.2008.12.018. [DOI] [PubMed] [Google Scholar]
- Volkmann J, Herzog J, Kopper F, Deuschl G. Introduction to the programming of deep brain stimulators. Movement disorders: official journal of the Movement Disorder Society. 2002;17(Suppl 3):S181–7. doi: 10.1002/mds.10162. [DOI] [PubMed] [Google Scholar]
- Wilson CJ, Beverlin B, 2nd, Netoff T. Chaotic desynchronization as the therapeutic mechanism of deep brain stimulation. Frontiers in systems neuroscience. 2011;5:50. doi: 10.3389/fnsys.2011.00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical journal. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]