Abstract
A new method for measuring bone mineral density (BMD) of the tarsal and metatarsals is described using volumetric quantitative computed tomography (VQCT) in subjects with diabetes mellitus and peripheral neuropathy. VQCT images of a single foot were acquired twice from eight subjects (mean age 51 [11 SD], seven males, one female). The cortical shells of the seven tarsal and five metatarsal bones were identified and semiautomatically segmented from adjacent bones. Volume and BMD of each bone were measured separately from the two acquired scans for each subject. Whole-bone semiautomatic segmentation measurement errors were determined as the root mean square coefficient of variation for the volume and BMD of 0.8% and 0.9%, respectively. In addition to the whole-bone segmentation methods, we performed atlas-based partitioning of subregions within the second metatarsal for all subjects, from which the volumes and BMDs were obtained for each subregion. The subregion measurement BMD errors (root mean square coefficient of variation) within the shaft, proximal end, and distal end were shown to vary by approximately 1% between the two scans of each subject. The new methods demonstrated large variations in BMDs between the 12 bones of the foot within a subject and between subjects, and between subregions within the second metatarsal. These methods can provide an important outcome measure for clinical research trials investigating the effects of interventions, aging, or disease progression on bone loss, or gain, in individual foot bones.
Key words: QCT, bone mineral density, foot, diabetes mellitus, peripheral neuropathy
Introduction
Both the National Institutes of Health (NIH) and the Food and Drug Administration (FDA) have highlighted the critical need for qualified biomarkers to speed drug development along the “Critical Path” from concept to commercial availability, to aid diagnosis and staging of disease and as indicators of disease progression and treatment outcomes1,2. Thus, there is an increasing emphasis on quantitative image analysis and techniques that may lead to the development of candidate image-based biomarkers. We are quantitatively assessing the bone mineral density (BMD) in foot bones to develop biomarkers of diabetic foot disease (i.e., neuropathic arthropathy, foot deformities, etc.) for (1) predicting outcomes, (2) following disease progression, and (3) measuring treatment efficacy3.
Bone mineral density (BMD) can be measured using: single-photon absorptiometry, dual-photon absorptiometry, radiographic absorptiometry, dual energy x-ray absorptiometry (DXA), and quantitative x-ray computed tomography (QCT)4. All of these techniques use ionizing radiation. DXA is the most widely applied technique in clinical practice because it is inexpensive, has a low radiation dose, and good reliability5. It is used commonly for measuring bone density in the lumbar spine and proximal femur, and less frequently in the forearm and calcaneus6. DXA has limitations when measuring the bone density for the entire bone since it is an areal projection imaging technique. With DXA, adjacent foot bones appear to “overlap” and are superimposed in the x-ray film. This limitation makes it nearly impossible to measure the bone density for individual bones in the foot.
Single-slice QCT, which is also a true volumetric density, has been predominantly used to measure trabecular BMD in the spine7. To image a trabecular region in the spine, typically, a single mid-slice with a given thickness is scanned instead of imaging the entire vertebrae. Single-slice QCT has limitations associated with measuring the same identical slice between subject visits. For vertebrae slice QCT, reliability errors are operator dependent and are influenced by patient positioning, slice location selection, and calibration phantom placement8. Registering the bones, so that the same identical slice is measured between subject visits, would be required to improve the reliability of the single slice method, but registration necessitates segmentation of the bone.
Volumetric QCT (VQCT) is a cross-sectional volumetric imaging technique capable of acquiring 3-dimensional (3D) or a volumetric image of the foot bones. The volumetric image of a single bone can be completely segmented (separated from surrounding bones). The segmented foot bone’s BMD and volume can be measured which eliminates the major limitations of DXA. VQCT is typically performed on standard clinical CT scanners and reliably measures volumetric BMD in the vertebrae and proximal femur9,10. We know of no previously published VQCT studies that segmented all of the tarsal and metatarsal bones and measured their BMD.
In addition to measuring the volume and BMD of an entire bone, measures within local regions in a bone may reveal: (1) differences in BMD spatial distribution between an individual’s right foot or left foot; or (2) local changes in volume and BMD within a bone over time. In bio-medical imaging, geometric atlases have been used to provide anatomical division within a segmented 2D anatomical structure, such as the mouse brain11. Annotated with predefined boundaries between subregions of the brain (such as cortex and thalamus), the atlas is registered onto the whole-brain segmentation in a 2D tissue image, yielding an internal partitioning of the brain into those subregions. So far, we know of no extensions of this approach to partition 3D subregions nor of other means for providing subregion measurement in VQCT scans of foot bones.
We developed new methods to assess the BMD in individual foot bones because diabetic foot diseases, such as acute neuropathic (Charcot’s) arthropathy, appear to affect BMD and cause considerable disability and morbidity12. The purpose of this paper is to describe the new methods for measuring the volume and BMD of each tarsal and metatarsal bone.
Materials and Methods
Subjects
Volumetric QCT images were collected from eight subjects with diabetes, peripheral neuropathy, and a history of forefoot or mid-foot plantar ulceration. The subject characteristics are shown in Table 1. Subjects were recruited from the Wound and Ostomy Center, Volunteers for Health, and the Diabetes Research Training Center at Washington University School of Medicine and BJC Health System, St. Louis, MO, USA. Prior to testing, informed consent was obtained from each subject according to an approved Washington University School of Medicine Human Research Protection Office protocol. Peripheral neuropathy was confirmed by assessing sensation to light touch (pressure) with Semmes–Weinstein monofilaments using a previously described technique13. All subjects were unable to feel the 5.07 (10 gram) monofilament on at least two sites on the plantar surface of the foot and had a history of plantar ulcers which confirmed they had peripheral neuropathy.
Table 1.
Subject Demographic Information
| Subject number | Age (years) | Weight (kg) | Height (m) | Body Mass Index (kg/m2) | Gender | Shoe Size | Length of DM (years) | Type of DM | HbA1c | Race | Foot |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 30 | 108.8 | 1.9 | 30.1 | Male | 48 | 11 | 2 | 11.6 | AA | Right |
| S2 | 54 | 146.9 | 1.8 | 47.8 | Male | 42 | 20 | 2 | 10 | C | Left |
| S3 | 51 | 88.2 | 1.85 | 25.8 | Male | 48 | 20 | 2 | 6.7 | C | Right |
| S4 | 45 | 155.2 | 1.9 | 43.0 | Male | 46 | 10 | 2 | 10.8 | AA | Right |
| S5 | 66 | 86.4 | 1.85 | 25.2 | Male | 46 | 2 | 2 | 9.3 | AA | Left |
| S6 | 61 | 110.9 | 1.77 | 35.4 | Male | 42 | 13 | 2 | 9.9 | C | Left |
| S7 | 49 | 108.6 | 1.8 | 33.5 | Male | 46 | 25 | 1 | 7.5 | C | Left |
| S8 | 55 | 171.3 | 1.8 | 52.9 | Female | 44 | 9 | 2 | 6.3 | AA | Right |
Note: Race: C — Caucasian, AA — African American. Shoe Size is given in European Shoe Size.
Image Acquisition
A Siemens Sensation 16 CT scanner was used to acquire the images from the eight subjects (Somatom Sensation 16, Siemens Medical Systems, Inc, Iselin, NJ, USA). The CT images were acquired using a previously documented procedure14–16. Briefly, the foot with the history of ulceration was selected for study. The subjects were seated with their foot resting on the table and their toes pointed away from their body. For each subject, their foot was scanned, repositioned, and scanned again. The following VQCT parameters were used to acquire the scans for all subjects: 12-mm table increment per gantry rotation, 16 × 0.75 mm collimation, 220 mAs, 120 kVp, with a pitch of 1, and a 512 × 512 matrix. The Sensation 16 has 16 parallel x-ray sources that were set to a collimation of 0.75 mm. Each subject’s foot was scanned from beyond the toes to above the talus. The acquisition time depended on the size of the subject’s foot. Approximately 200 to 300 mm of data was acquired. The VQCT projection data sets were reconstructed at 0.75-mm reconstruction intervals at the CT scanner to create the VQCT images.
A solid QCT-Bone Mineral™ Phantom (Image Analysis, Inc., Serial No. 4225) was used to determine that the CT scanner had low variability between scans within a session and between scanning sessions. The phantom was constructed of three different calcium hydroxyapatite samples (200, 100, 50 mg/cc calcium hydroxyapatite) incorporated in a water equivalent compound. The phantom was repeatedly scanned on the same day (session) and between days (sessions).
Whole-Bone Semiautomatic Segmentation
VQCT images of the foot was imported into the Analyze17,18 software program and resampled to 0.7-mm isotropic voxels (Fig. 1a) in preparation for segmentation. Segmentation of an individual region of interest (i.e., bones) from the VQCT images is an important step when measuring BMD. Numerous segmentation techniques are available19–21. Our approach for segmentation of whole foot bones from the soft tissue was based on edge detection filtering22. The resampled volumetric data was imported into ImageJ (a public domain Java image processing program developed at the National Institutes of Health)23 for identifying the boundaries (cortical shells) of the bones with an edge detection filter. Filtering allows the grayscale volumetric image to be reduced to a binary representation. All voxels located on edges (boundaries between two different tissue types) are set to a binary 1 and the remaining voxels are set to a binary 0. Since each bone in the foot consists of a cortical shell and trabecular internal region, identifying the cortical shell was sufficient as a means to identify the boundary of each bone.
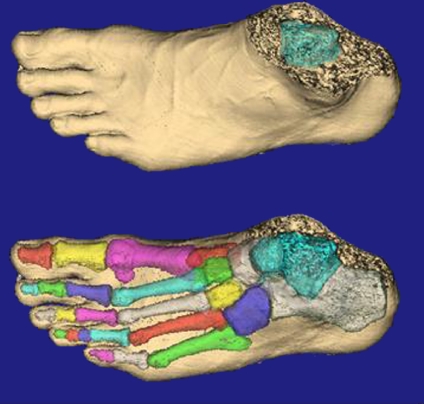
Fig 1.
Volume rendered QCT images from a healthy subject: (a) soft-tissue representation (top), and (b) individually isolated bone representation within the skin surface overlay.
After the boundaries of the bones were collectively determined using the edge detection filter, we used editing tools and morphology operations to separate the individual bones in the binary image18,24. The entire boundary of each bone was nearly completely isolated from the surrounding bones by the edge detection filter due to joint spaces between bones, but in locations where the bones were either touching or nearly touching, connections between the bones were manually deleted. After removal of the connections, any place in the cortical boundary where a gap was identified, the operator would manually fill in the gap. The gaps were typically small (i.e., just a few voxels). Occasionally, larger gaps would be created by an extremely thin cortical shell, which required manual filling. Then, internal holes found in the segmented bone resulting from marrow spaces were filled automatically using the fill morphology operator. Binary mathematical morphology is a process used to manipulate an object of interest18,24. After breaking the connections and filling the holes, the operator utilized auto-trace to define each of the 12 tarsal and metatarsal bones as independent objects (Fig. 1b). The binary representation of the individually segmented bones was multiplied by the original volumetric grayscale data to extract the grayscale values for each tarsal and metatarsal bone.
Whole-Bone Semiautomatic Measurement
Volume and BMD of each whole tarsal and metatarsal bone was measured from the two acquired scans for each subject with the measurement for scan one separated by approximately 1 month from scan 2. The volume and mean Hounsfield units (HU) were computed (measured) for each bone from the extracted grayscale data. HU is a quantitative measure of the x-ray attenuation coefficients (radiodensity) of tissues in computed tomography. In this paper, BMD is given in HU. Typically, HU is converted to BMD because a direct linear relationship exists between HU and BMD10,25, but this is true when trabecular BMD values fall in a range where the CT scanner has been calibrated. The solid QCT-Bone MineralTM Phantom only has BMD values ranging from 0 to 0.200 g/cc and is used to calibrate the CT scanner in the trabecular BMD range. The cortical bone in many of the foot bones ranges from approximately 500 HU to 2000 HU. To our knowledge, we have not been able to find any papers or phantoms that calibrate a CT scanner in the 500 HU to 2000 HU range for making cortical BMD measurements. We are in the process of developing our own CT calibration phantom(s) and methods to convert HU to BMD (g/cc) over a wide range of values from 0 to 2000 HU. The error between measurements from the repeated CT scans for the eight subjects was determined for the foot. The mean time required to segment and measure the 12 foot bones (five metatarsals and seven tarsals) for a single subject was approximately 2.4 (±0.67) h.
Subdivision Atlas Measurement of the Second Metatarsal
While the semiautomatic segmentation method allows for measurement of volumes and BMD of whole individual bones, we were further interested in developing methods for obtaining measures within subregions of a bone. The second metatarsal was utilized to demonstrate our subregion (proximal end, distal end, and the shaft) measurement capability within and between subjects. The second metatarsal is often associated with deformity (hammer toe), stress fractures, and fracture dislocations26,27. In addition, the length of the second metatarsal allowed us to create subregions along its length. These subregions allow inherent differences in BMD between the proximal end, shaft, and distal end to be measured. Note that the semiautomatic segmentation method discussed above could not have been utilized for partitioning these three subregions due to the poor contrast ratio between subregions in a bone (e.g., between the proximal end and shaft of a metatarsal). To overcome such difficulty, we extended the atlas-based 2D subregion partitioning approach reported by Ju et al.11 to a 3D VQCT volume.
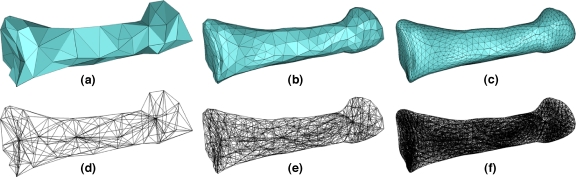
We utilized a volumetric subdivision atlas to model the partitioning of a bone into subregions. Subdivision is a fractal-like process that models a smooth shape by iterative refinement of an initial, coarse shape. Figure 2a,d shows an example atlas of a second metatarsal modeled as a tetrahedral subdivision mesh. Applying subdivision rules28, this coarse atlas is refined in successive subdivision levels into smaller tetrahedral and octahedral elements with a smoother appearance. Figure 2b,e and c, f show the atlases after one and two rounds of subdivision. This atlas was constructed from one metatarsal semiautomatically segmented from a VQCT scan by applying standard surface simplification29 and tetrahedral meshing30 to the segmented bone surface. To further define the subregions, we labeled the interior elements of the atlas at a chosen subdivision level (we used 2) that belong to each subregion. Specifically, we computed an axis of the shaft of the atlas and partitioned all atlas elements using two planes, one located at a distance of 20% from the proximal end and the other at a distance of 20% from the distal end, as shown in Figure 3. These two planes partitioned the metatarsal into three subregions denoted as follows: (1) proximal end, (2) shaft, and (3) distal end (metatarsal head).
Fig 2.
The subdivision atlas of a second metatarsal at base level (a, d) and after subdividing once (b, e) and twice (c, f). The top row shows the exterior triangulated surface of the atlas while the bottom row shows the wire frame internal tetrahedral and octahedral elements.
Fig 3.
(a) Labeling the second metatarsal atlas using two planes perpendicular to the shaft axis (colored yellow), (b) one at a distance of 20% from the proximal end, and (c) one at 20% from the distal end. The colored dots show the BMD of a registered bone scan within each element in the whole registered atlas (a) or within labeled subregions (b, c). High and low BMD values are shown as red and blue, respectively.
After the atlas construction and element labeling, we partitioned the subregions in a new scan by registering the atlas onto the scan. Subdivision was useful because the geometry of the refined atlas was completely determined by the geometry of the initial, base-level atlas, which offered easy control for registering the atlas onto a second structure. Similar to the methods described by Ju et al.11, we registered the atlas with a segmented bone surface in two steps. First, the atlas was aligned to the bone surface using global transformations (e.g., translation, scaling and rotation) obtained by Principle Component Analysis. Next, the location of each individual vertex in the base-level atlas was locally perturbed. The local alignment step was performed in an iterative process that minimized the distance between the outer boundary of the refined atlas to the target as well as the amount of distortion introduced to the interior elements. We adopted the same process described by Ju et al.11 while extending the distortion term designed for 2D triangular elements onto 3D tetrahedral elements. Specifically, we let F be the set of interior triangular faces shared by two tetrahedrons in the initial atlas, vi and 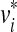 the location of the i-th vertex in the atlas before and after alignment, p, q the indices of the other two vertices in the two tetrahedra sharing the face {vi, vj, vk}, and Aijkp the unsigned volume of the tetrahedron formed by vertices {vi, vj, vk, vp}. The distortion of the atlas interior after alignment is measured as the deviation of the alignment from an affine transformation:
the location of the i-th vertex in the atlas before and after alignment, p, q the indices of the other two vertices in the two tetrahedra sharing the face {vi, vj, vk}, and Aijkp the unsigned volume of the tetrahedron formed by vertices {vi, vj, vk, vp}. The distortion of the atlas interior after alignment is measured as the deviation of the alignment from an affine transformation:
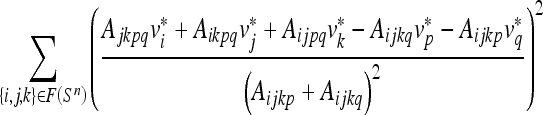 |
1 |
Following registration, the volume and BMD for each subregion was computed by summing the volume and BMD within each tetrahedral and octahedral element belonging to that subregion in the registered atlas at the chosen subdivision level (linear interpolation is used when the vertices of the elements do not fall on integer coordinates).
Results
The mean HU for the phantom varied by approximately 1.5 HU or less between the two scanning sessions. The calibration phantom results demonstrated that the CT scanner had low variability between scans in a session and between sessions.
Whole-Bone Semiautomatic Segmentation Measures
The volume of the seven tarsal and five metatarsal bones was computed for the eight subjects’ initial foot scans and for their repeated foot scans to determine the volume measurements error in the semiautomatic segmentation method.
The BMDs for each of the seven tarsal and five metatarsal bones (cortical and trabecular regions combined for each bone) were computed for the eight subjects’ initial foot scans and for their repeated foot scans (Table 2). Since no previously published data exist for the tarsal and metatarsal bones, the individual BMD measurements for each bone were reported to demonstrate the variation in BMD for the individual bones within a subject’s foot and between the feet for each of the subjects. The BMD variation can be seen for the individual bones within a subject’s foot and between the feet for the subjects. For the eight subjects, the 2nd metatarsal had the highest mean density (mean 577 HU) and the cuboid had the lowest mean density (mean 314 HU) (Table 2, rightmost two columns). The BMD for each subject’s five metatarsals were typically higher (mean 494 HU) than the tarsal bones (mean 414 HU). The higher BMD values for the metatarsals likely are due to the large volume of cortical bone, especially in the shafts, whereas the tarsal bones are comprised predominately of trabecular bone. The sesmoids were not measured and were not included in the first metatarsal BMD measurements.
Table 2.
BMD (Radiographic Density) Measurements from Repeated Scans for Each Tarsal and Metatarsal Bone in the Foot
| BMD (HU) | Subject Number (SN) — scan number | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Foot Bones | S1-1 | S1-2 | S2-1 | S2-2 | S3-1 | S3-2 | S4-1 | S4-2 | S5-1 | S5-2 | S6-1 | S6-2 | S7-1 | S7-2 | S8-1 | S8-2 | Mean | SD |
| Metatarsal 1 | 513 | 506 | 519 | 512 | 375 | 375 | 543 | 529 | 366 | 371 | 448 | 455 | 293 | 294 | 367 | 363 | 427 | 89 |
| Metatarsal 2 | 659 | 656 | 705 | 693 | 504 | 506 | 755 | 739 | 530 | 534 | 568 | 573 | 419 | 420 | 483 | 482 | 577 | 114 |
| Metatarsal 3 | 526 | 534 | 577 | 565 | 470 | 472 | 771 | 755 | 366 | 375 | 486 | 494 | 280 | 281 | 444 | 444 | 490 | 143 |
| Metatarsal 4 | 588 | 589 | 558 | 545 | 527 | 529 | 716 | 692 | 305 | 312 | 418 | 424 | 282 | 284 | 491 | 487 | 484 | 142 |
| Metatarsal 5 | 547 | 551 | 571 | 560 | 561 | 559 | 706 | 686 | 343 | 359 | 384 | 396 | 327 | 328 | 491 | 487 | 491 | 127 |
| Cuneiform 1 | 505 | 497 | 530 | 519 | 358 | 359 | 632 | 624 | 408 | 409 | 410 | 415 | 251 | 252 | 379 | 373 | 433 | 116 |
| Cuneiform 2 | 561 | 555 | 530 | 526 | 418 | 420 | 695 | 692 | 441 | 443 | 466 | 474 | 318 | 319 | 394 | 390 | 478 | 115 |
| Cuneiform 3 | 382 | 382 | 412 | 411 | 314 | 316 | 598 | 593 | 327 | 330 | 399 | 402 | 231 | 232 | 335 | 336 | 375 | 106 |
| Cuboid | 330 | 324 | 355 | 345 | 272 | 274 | 493 | 486 | 262 | 266 | 294 | 300 | 211 | 211 | 303 | 303 | 314 | 82 |
| Navicular | 553 | 545 | 533 | 526 | 406 | 407 | 722 | 719 | 435 | 437 | 491 | 493 | 258 | 258 | 451 | 456 | 481 | 132 |
| Talus | 490 | 489 | 516 | 514 | 760 | 759 | 404 | 405 | 470 | 472 | 282 | 283 | 483 | 485 | 487 | 144 | ||
| Calcaneus | 340 | 337 | 401 | 399 | 288 | 287 | 487 | 486 | 259 | 260 | 330 | 330 | 224 | 224 | 342 | 341 | 333 | 82 |
| SN-Mean | 500 | 497 | 517 | 510 | 408 | 409 | 657 | 647 | 371 | 375 | 430 | 436 | 281 | 282 | 414 | 412 | ||
| SN-SD | 101 | 101 | 93 | 91 | 98 | 98 | 103 | 101 | 79 | 78 | 75 | 75 | 56 | 56 | 68 | 68 | ||
The values are given in Hounsfield units (HU) for each bone
Subdivision Atlas Segmentation Measures
The volume and BMD for the whole second metatarsal was computed from the eight subject’s initial scans and for their repeated foot scans using the subdivision atlas method. The volume and BMD for the whole second metatarsal were measured for comparing the accuracy of the subdivision atlas segmentation method to the semiautomatic segmentation method of measuring.
The BMDs for the second metatarsal’s three subregions (proximal end, shaft, and distal end) were computed from the subdivision’s results for the eight subject’s initial scans (Table 3) and for their repeated foot scans. The mean BMD from the eight subjects for the second metatarsal shaft was approximately 160% more dense (782.4 HU compared to 298.8 HU) compared to the distal end (metatarsal head) and approximately 63% more dense (782.4 HU compared to 480.5 HU) compared to the proximal end (metatarsal base).
Table 3.
Subregion (Proximal, Shaft, and Distal End) BMD Measurements are Given for Scan One of the Second Metatarsal Using the Subdivision Atlas Method
| Subject | Prox. BMD | Shaft BMD | Distal BMD |
|---|---|---|---|
| S1 | 587.2 | 866.7 | 305.8 |
| S2 | 595.6 | 933.4 | 379.1 |
| S3 | 379.9 | 712.5 | 297.5 |
| S4 | 674.1 | 929.5 | 472.8 |
| S5 | 434.7 | 721.3 | 243.7 |
| S6 | 442.5 | 788.5 | 294.4 |
| S7 | 322.4 | 599.1 | 201.4 |
| S8 | 407.6 | 708.3 | 196.0 |
| Mean | 480.5 | 782.4 | 298.8 |
| SD | 123.1 | 119.1 | 92.5 |
Error in the Semiautomatic Segmentation Measures
The error in the semiautomatic segmentation measurements was computed for each bone by subtracting the first scan from the second scan for each of the eight subjects. For absolute errors, the error was computed as the bias (mean) and root mean square standard deviation (SDRMS) of the difference measures for the seven tarsal and the five metatarsal bones (Table 4)31. The bias was small for both the volume and BMD measurements. The mean volume and BMD reliability (SDRMS) for the 12 bones was 0.12 cc and 4.2 HU, respectively.
Table 4.
The Bias (Mean), Root Mean Square Standard Deviation (SDrms) and Root Mean Square Coefficient of Variation (CVrms) for the Difference Measures of Repeated Scans Obtained from Each Tarsal and Metatarsal Bone in the Foot
| Difference Measures | Difference Measures | |||||
|---|---|---|---|---|---|---|
| Volume | BMD | Volume | BMD | |||
| Foot Bones | Mean | SDRMS | Mean | SDRMS | CVRMS (%) | CVRMS (%) |
| Metatarsal 1 | 0.00 | 0.07 | −2.4 | 4.9 | 0.3 | 1.1 |
| Metatarsal 2 | 0.00 | 0.04 | −2.5 | 5.3 | 0.3 | 0.9 |
| Metatarsal 3 | −0.01 | 0.05 | 0.0 | 6.2 | 0.5 | 1.3 |
| Metatarsal 4 | 0.05 | 0.08 | −2.9 | 7.3 | 0.8 | 1.5 |
| Metatarsal 5 | 0.02 | 0.07 | −0.5 | 7.7 | 0.7 | 1.6 |
| Cuneiform 1 | −0.10 | 0.18 | −3.1 | 4.4 | 1.4 | 1.0 |
| Cuneiform 2 | −0.03 | 0.07 | −0.5 | 3.1 | 1.4 | 0.6 |
| Cuneiform 3 | −0.08 | 0.09 | 0.5 | 1.8 | 1.2 | 0.5 |
| Cuboid | −0.13 | 0.22 | −1.4 | 3.9 | 1.3 | 1.2 |
| Navicular | −0.16 | 0.21 | −1.0 | 3.1 | 1.4 | 0.6 |
| Talus | −0.17 | 0.15 | 0.3 | 1.1 | 0.3 | 0.2 |
| Calcaneus | −0.18 | 0.25 | −0.9 | 1.0 | 0.3 | 0.3 |
| Mean | −0.07 | 0.12 | −1.2 | 4.2 | 0.8 | 0.9 |
The volume differences are given in cubic centimeters (cm3) for each bone and the BMD values are given in Hounsfield units (HU) for each bone
For relative errors, the root mean square coefficient of variation (CVRMS) was computed using the methods described by Gluer et. al. (Table 4)31. We computed the CVRMS to allow interpretation of the standard deviation in relationship to the size of the mean for each bone. The CVRMS allows for comparison of the errors between the bones. The mean CVRMS for measuring the volume and BMD for the 12 bones was 0.8% and 0.9%, respectively. The metatarsals had the largest BMD CVRMS ranging from 0.9% for 2nd metatarsal to 1.6% for the 5th metatarsal. The talus and calcaneus had the smallest BMD CVRMS of 0.2% and 0.3%, respectively, but these two bones had the largest volume out of the 12 bones. The volume CVRMS for the five metatarsals and seven tarsal bones was 0.5% and 1.0%, respectively. The BMD CVRMS for the five metatarsals and seven tarsal bones was 1.3% and 0.6%, respectively.
Error in the Subdivision Atlas Segmentation Measures
To evaluate the quality of the atlas-based subregion segmentation, we registered the bone atlas onto the eight subjects’ repeated CT scans. The whole-bone volume and BMD bias (mean), root mean square standard deviation (SDRMS), and the root mean square coefficient of variation (CVRMS) of the difference measures between the repeated CT scans are reported in Table 531 as well as for each subregion. Note that the volume and BMD of any subregion differed by approximately 1% or less between the two scans, demonstrating the small error in segmentation with respect to orientation and position differences between bones. In addition, the volume and BMD of the whole-bone atlas measurement differed from the whole bone measured by the semiautomatic segmentation method on average −0.01% (0.05%) and −0.02% (0.11%), respectively, demonstrating the accuracy of the atlas registration method.
Table 5.
Whole-Bone and Subregion (Proximal, Shaft, and Distal End) Volume and BMD Bias (Mean), Root Mean Square Standard Deviation (SDrms) and Root Mean Square Coefficient of Variation (CVrms) for the Difference Measures of Repeated Scans Obtained for the Second Metatarsal Using the Subdivision Atlas Method
| Difference Measures | Difference Measures | |||||
|---|---|---|---|---|---|---|
| Volume | BMD | Volume | BMD | |||
| Foot Bones | Mean | SDRMS | Mean | SDRMS | CVRMS (%) | CVRMS (%) |
| Metatarsal 2 | 0.00 | 0.03 | −2.44 | 5.5 | 0.3 | 1.0 |
| Met2 Prox. | 0.00 | 0.03 | −2.26 | 3.6 | 0.7 | 0.8 |
| Met2 Shaft | −0.02 | 0.03 | −0.95 | 8.0 | 0.6 | 1.0 |
| Met2 Distal | 0.02 | 0.02 | −1.46 | 3.9 | 0.9 | 1.3 |
| Mean | 0.00 | 0.03 | −1.78 | 5.2 | 0.6 | 1.0 |
Discussion
Measuring BMD and volume of bones in the foot has a number of important clinical research applications. People with diabetes and peripheral neuropathy are at risk for developing neuropathic (Charcot’s) arthropathy, a chronic progressive disease potentially affecting all bones in the foot. Neuropathic (Charcot’s) arthropathy is characterized by rapid and profound destruction of the joints and bones32. Previously, there was not a method available for measuring the volume and BMD of each of the tarsal and metatarsal bones in the foot. Even those with diabetes, but without peripheral neuropathy, are at increased risk of foot fracture. Schartz et al.33 mentioned that more research is needed to investigate the efficacy of current treatments to improve bone strength among women with diabetes. Besides those with diabetes, Hasselman et al.34 stated that a major public health goal should be to identify specific risk factors and methods to help prevent foot and ankle fractures in older women. With a reliable method for measuring the volume and BMD in the foot, and a reliable means for monitoring local variations in these measures, new studies investigating BMDs in the feet could be conducted to reach these goals. Our new methods will allow researchers to study foot BMDs in subjects at risk for fracture or arthropathy to determine if there is an association between fractures and low foot BMDs. If an association is found, these measurement methods could be used as a non-invasive biomarker for determining the effect of various interventions (i.e., medications or exercise) on foot bone volume and BMD.
The repeated measurement results from our VQCT study of bones in the foot are similar to VQCT studies conducted by Kang et al.10 (femoral neck) and Mastmeyer et al.9 (lumbar spine). Our repeated measurement results for segmented volume and BMD were 0.8% and 0.9%, respectively, compared to 2.0% and 0.6%, respectively, for the lumbar spine results reported by Mastmeyer et al. Kang et al. repeated measurement results were less than 1% for volume and BMD from slice and spherical volumes of interest for the femoral neck. From our study, we found the mean BMD repeated measurements to be 0.9% and range from 0.2% to 1.6% for the 12 bones and is better than those found in previous slice QCT studies35,36. The reliability of single slice QCT is 2% to 4%37,38, which is higher than those observed for posteroanterior DXA, but is comparable with those of lateral DXA37,38. However, VQCT can be used to selectively assess individual bone volume and BMD without overlapping bones unlike projection methods such as DXA. As the effective radiation dose involved in VQCT is generally low and is comparable to less than 1-month exposure to natural radiation39, utilizing VQCT to acquire BMD in subjects is low risk. In particular, a peripheral VQCT scan does not expose sensitive organs, thereby posing even less biological risk.
We found that the BMD for the metatarsal and tarsal bones varies greatly within an individual’s foot and between subjects with diabetes and peripheral neuropathy (Table 2). As an example, the BMD of metatarsal 2 was two times the BMD of the cuboid for Subject 1 (659 vs 330 HU, Table 2). Between subjects, mean BMD varied from a low of 282 HU (S7) to a high of 657 HU (S4). We believe this high variation of BMD between an individual’s own foot bones and between subjects emphasizes the need to measure BMD in each foot bone as opposed to measuring BMD in only one bone. The result of one bone cannot represent the values from all bones of the foot.
There are several potential limitations associated with this study. First, the sample size is small. Despite the small sample size, however, the measurement differences (Table 4) were consistently low across all subjects and bones. Additional research using larger samples is needed to establish intra- and inter-measurement reliability of the methods. Also, the percent difference errors (Table 5) for the subregion measurements were only obtained for the second metatarsal. The subregion measurements should be applied to all metatarsals and tarsals in a reliability study with a larger subject population. The consistency of the results from the subregion measurements suggests that similar results would be obtained using other metatarsals or tarsal bones. Second, the bone density phantom was not placed into the scan volume for each subject to allow direct conversion of HU to BMD mg/cc10. We do not think this is a major limitation, however, because the variation of HU measured between bones in a subject’s foot was large (range from 56 to 103 HU) compared to the small variation found in the density of the phantom measured between VQCT sessions (approximately 1.5 HU). This small variation demonstrated the short term measurement stability of the CT scanner. Third, the mean time required to segment and measure the 12 bones for a subject was approximately 2.4 (±0.67) h, though we are working on methods to substantially reduce this time. Since all 12 bones were processed on average in 2.4 h, the time to process a single bone, on average, was approximately 12 min. Once the bones were segmented and the bone volume computed, calculating the BMD for all 12 bones required only a few minutes.
We have presented a method to semiautomatically segment all tarsal and metatarsal bones from the foot to measure their volume and BMD. The results of this study demonstrate that we can repeatedly segment the whole bone and subregions within a bone. The small measurement error in volume and BMD measures for each of the metatarsal and tarsal bones in the foot demonstrate the small repeated measurement errors for the methods. In addition, we show that the whole-bone segmentation can be used as a basis for further local analysis within a bone, such as subregion partitioning making use of a geometric atlas. The subdivision atlas methods can also be applied to any bone in the foot. Foot bones can be collectively grouped (forefoot, mid-foot and hind foot, or medial/lateral columns) to determine mean BMDs for particular foot regions. Armstrong et al. found the prevalence of foot deformities in subjects with neuropathic arthropathy to be 48% at the tarso-metatarsal (Lisfrac’s) joint and 34% at Chopart’s joint32. Therefore, we would expect the BMD of bones surrounding these joints to be the most affected by foot deformities and the deformities would be the major cause of ulcers. We are aware of no other published study where the bone density for all of the metatarsal and tarsal bones or their subregions have been measured and reported. Kang et al.10 have developed a volumetric semiautomated method of measuring the volume and BMD of the femoral neck and compared their results to slice QCT, but they have not applied this method to bones in the foot. Mastmeyer et al.9 have performed 3D segmentation of the lumbar spine for measuring BMD from volumetric QCT. We were successful in developing a new VQCT method for imaging and segmenting each tarsal and metatarsal bone to be used in studies of subjects with diabetic foot disease.
Conclusion
We met our objective to develop a new, repeatable method of segmenting each tarsal and metatarsal bone, and determined their BMDs. The results of this study showed that we can repeatedly segment each tarsal and metatarsal bone to measure its volume and BMD. We are currently utilizing these methods to develop specific biomarkers for neuropathic (Charcot’s) arthropathy in patients with chronic diabetes3.
Acknowledgments
We would like to thank Dr. Fred W. Prior for his collaborative support of this project. We would also like to thank Ryan Goldberg for his repeated measurements of the eight subjects with diabetes and peripheral neuropathy. Funding was provided by the National Institutes of Health, National Center of Medical Rehabilitation and Research (RO1 HD36895) and National Institute of Diabetes and Digestive and Kidney Diseases (R21 DK079457). The authors acknowledge the Prevention and Control Research Core of the Washington University Diabetes Research and Training Center (P60 DK20579) for their assistance in subject recruitment. We thank Richard Robb and his associates of the Mayo Biomedical Imaging Resource, Rochester, MN, for providing the Analyze software.
This study was supported by the National Center for Medical Rehabilitation Research and National Institute of Diabetes and Digestive and Kidney Diseases and the National Institutes of Health Grants.
References
- 1.http://www.fda.gov/oc/initiatives/criticalpath/whitepaper.html. U.S. Food and Drug Administration. Accessed 18 February 2008
- 2.Biomarkers definitions working group Commentary: Biomarkers and surrogate endpoints: preferred definitions and conceptual framework. Clin Pharmacol Ther. 2001;69(3):89–95. doi: 10.1067/mcp.2001.113989. [DOI] [PubMed] [Google Scholar]
- 3.Prior F, Commean PK, Ju T, Hastings MK, Hildebolt CF, Sinacore DR: Developing a biomarker for neuropathic arthropathy in diabetic patients. 2007 IEEE/NIH Life Science Systems and Applications Workshop (LISSA 2007)
- 4.Bonnick SL. Bone Densitometry in Clinical Practice. Totowa, NJ: Humana Press; 2004. [Google Scholar]
- 5.Genant HK, Engelke K, Fuerst T, et al. Noninvasive assessment of bone mineral and structure: state of the art. J Bone Miner Res. 1996;11:707–730. doi: 10.1002/jbmr.5650110602. [DOI] [PubMed] [Google Scholar]
- 6.Njeh CF, Genant HK. Bone loss: quantitative imaging techniques for assessing bone mass in rheumatoid arthritis. Arthritis Res. 2000;2(6):446–450. doi: 10.1186/ar126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jergas M, Breitenseher M, Gluer CC, Yu W, Genant HK. Estimates of volumetric bone density from projectional measurements improve the discriminatory capability of dual X-ray absorptiometry. J Bone Miner Res. 1995;10:1101–1110. doi: 10.1002/jbmr.5650100715. [DOI] [PubMed] [Google Scholar]
- 8.Lang TF, Li J, Harris ST, Genant HK. Assessment of vertebral bone mineral density using volumetric quantitative CT. J Comput Assist Tomogr. 1999;23(1):130–7. doi: 10.1097/00004728-199901000-00027. [DOI] [PubMed] [Google Scholar]
- 9.Mastmeyer A, Engelke K, Fuchs C, Kalender WA. A hierarchical 3D segmentation method and the definition of vertebral body coordinate systems for QCT of the lumbar spine. Med Image Anal. 2006;10(4):560–77. doi: 10.1016/j.media.2006.05.005. [DOI] [PubMed] [Google Scholar]
- 10.Kang Y, Engelke K, Fuchs C, Kalender WA. An anatomic coordinate system of the femoral neck for highly reproducible BMD measurements using 3D QCT. Comput Med Imaging Graph. 2005;29(7):533–41. doi: 10.1016/j.compmedimag.2005.05.002. [DOI] [PubMed] [Google Scholar]
- 11.Ju T, Warren J, Eichele G, Thaller C, Chiu W, Carson J: A geometry database for gene expression data. In: Proceedings of Eurographics Symposium on Geometry Processing, pages 166–176, 2003 [PMC free article] [PubMed]
- 12.Fabrin J, Larsen K, Hostein PE. Long-term follow-up in diabetic Charcot feet with spontaneous onset. Diabetes Care. 2000;23(6):796–800. doi: 10.2337/diacare.23.6.796. [DOI] [PubMed] [Google Scholar]
- 13.Diamond JE, Mueller MJ, Delitto A, Sinacore DR. Reliability of a diabetic foot evaluation. Phys Ther. 1989;69:797–802. doi: 10.1093/ptj/69.10.797. [DOI] [PubMed] [Google Scholar]
- 14.Lott DJ, Hastings MK, Commean PK, Smith KE, Mueller MJ. Effect of footwear and orthotic devices on stress reduction and soft tissue strain of the neuropathic foot. Clin Biomech. 2007;22(3):352–359. doi: 10.1016/j.clinbiomech.2006.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Commean PK, Mueller MJ, Smith KE, et al. Reliability and validity of combined imaging and pressures assessment methods for diabetic feet. Arch Phys Med Rehabil. 2002;83:497–505. doi: 10.1053/apmr.2002.30923. [DOI] [PubMed] [Google Scholar]
- 16.Mueller MJ, Smith KE, Commean PK, Robertson DD, Johnson JE. Use of computed tomography and plantar pressure measurement for management of neuropathic ulcers in patients with diabetes. Phys Ther. 1999;79:296–307. [PubMed] [Google Scholar]
- 17.Robb RA, Hanson DP, Karwoski RA, Larson AG, Workman EL, Stacy MC. Analyze: a comprehensive, operator-interactive software package for multidimensional medical image display and analysis. Comput Med Imaging Graph. 1989;13:433–454. doi: 10.1016/0895-6111(89)90285-1. [DOI] [PubMed] [Google Scholar]
- 18.Robb RA. Three Dimensional Biomedical Imaging: Principles and Practice. New York: VCH Publishers; 1995. [Google Scholar]
- 19.Fu KS, Mui JK. A survey on image segmentation. Pattern Recogn. 1981;13:3–16. doi: 10.1016/0031-3203(81)90028-5. [DOI] [Google Scholar]
- 20.Zijdenbos AP, Dawant BM. Brain segmentation and white matter lesion detection in MR images. Crit Rev Biomed Eng. 1994;22:401–465. [PubMed] [Google Scholar]
- 21.Sonka M, Fitzpatrick JM: Handbook of Medical Imaging: Medical Image Processing and Analysis. In (vol 2). Bellingham, WA: SPIE (The International Society for Optical Engineering), 2000
- 22.Russ JC. The Image Processing Handbook, 2nd Edition. Boca Raton, FL: CRC Press; 1995. [Google Scholar]
- 23.Girish V, Vijayalakshmi A. (http://rsb.info.nih.gov/ij/) Affordable image analysis using NIH Image/ImageJ. Indian J Cancer. 2004;41(1):47. [PubMed] [Google Scholar]
- 24.Hohne KH, Hanson WA. Interactive 3D segmentation of MRI and CT volumes using morphological operations. J Comput Assist Tomogr. 1992;16:285–294. doi: 10.1097/00004728-199203000-00019. [DOI] [PubMed] [Google Scholar]
- 25.Kalender WA, Klotz E, Suss C. Vertebral bone mineral analysis: an integrated approach with CT. Radiology. 1987;164:19–23. doi: 10.1148/radiology.164.2.3602380. [DOI] [PubMed] [Google Scholar]
- 26.Burroughs KE, Reimer CD, Fields KB. Lisfranc injury of the foot: a commonly missed diagnosis. Am Fam Physician. 1998;58:118–24. [PubMed] [Google Scholar]
- 27.Robertson DD, Mueller MJ, Smith KE, Commean PK, Pilgram T, Johnson J. Forefoot structural change in individuals with diabetes and prior plantar ulcer. J Bone Jt Surg Am vol. (ed), 2002;84–A(8):1395–1404. doi: 10.2106/00004623-200208000-00016. [DOI] [PubMed] [Google Scholar]
- 28.Schaefer S, Hakenberg J, Warren J: Smooth subdivision of tetrahedral meshes. In Proceedings of Eurographics Symposium on Geometry Processing, 2004, pages 151–158
- 29.Garland M, Heckbert P: Surface Simplification Using Quadric Error Metrics. Proceedings of SIGGRAPH 97, 1997, pp. 209–216
- 30.Shewchuk JR: Tetrahedral mesh generation by Delaunay refinement. In SCG’98: Proceedings of the fourteenth annual symposium on Computational geometry. ACM Press, New York, NY, USA, 1998, pages 86–95
- 31.Gluer CC, Blake G, Lu Y, Blunt BA, Jergas M, Genant HK. Accurate assessment of precision errors: how to measure the reproducibility of bone densitometry techniques. Osteoporos Int. 1995;5(4):262–270. doi: 10.1007/BF01774016. [DOI] [PubMed] [Google Scholar]
- 32.Armstrong DG, Todd WF, Lavery LA, et al. The natural history of acute Charcot’s arthropathy in a diabetic foot specialty clinic. J Am Podiatr Med Assoc. 1997;87(6):272–278. doi: 10.7547/87507315-87-6-272. [DOI] [PubMed] [Google Scholar]
- 33.Schartz AV, Sellmeyer DE, Ensrud KE, et al. Older women with diabetes have an increased risk of fracture: a prospective study. J Clin Endocrinol Metab. 2001;86(1):32–38. doi: 10.1210/jc.86.1.32. [DOI] [PubMed] [Google Scholar]
- 34.Hasselman CT, Vogt MT, Stone KL, Cauley JA, Conti SF. Foot and ankle fractures in elderly white women: Incidence and risk factors. J Bone Jt Surg. 2003;85:820–824. doi: 10.2106/00004623-200305000-00008. [DOI] [PubMed] [Google Scholar]
- 35.Rosenthal DI, Ganott MA, Wyshak G, Slovik DM, Doppelt SH, Neer RM. Quantitative computed tomography for spinal density measurement. Factors affecting precision. Invest Radiol. 1985;20:306–310. doi: 10.1097/00004424-198505000-00014. [DOI] [PubMed] [Google Scholar]
- 36.Graves VB, Wimmer R. Long-term reproducibility of quantitative computed tomography vertebral mineral measurements. J Comput Tomogr. 1985;9:73–76. doi: 10.1016/0149-936X(85)90053-0. [DOI] [PubMed] [Google Scholar]
- 37.Pouilles JM, Tremollieres F, Todorovsky N, Ribot C. Precision and sensitivity of dual-energy x-ray absorptiometry in spinal osteoporosis. J Bone Miner Res. 1991;6:997–1002. doi: 10.1002/jbmr.5650060914. [DOI] [PubMed] [Google Scholar]
- 38.Lees B, Stevenson JC. An evaluation of dual-energy X-ray absorptiometry and comparison with dual-photon absorptiometry. Osteoporos Int. 1992;2:146–152. doi: 10.1007/BF01623822. [DOI] [PubMed] [Google Scholar]
- 39.Cann CE. Quantitative CT for determination of bone mineral density: a review. Radiology. 1988;166:509–522. doi: 10.1148/radiology.166.2.3275985. [DOI] [PubMed] [Google Scholar]